| CATEGORII DOCUMENTE |
STRUCTURI DE TIP GRAF
1 Reprezentarea matriciala a grafurilor
Definitie:
Se numeste graf neorientat o pereche ordonata de multimi G=(V,E), unde V este o multime finita nevida de elemente, iar E este formata din perechi neordonate de elemente din V.
Multimea E se numeste multimea muchiilor grafului G. Notam prin (xi, xj) muchia formata din virfurile xi si xj din V (multimea varfurilor).
Daca perechea (x, y) apartine lui E, se spune ca virfurile x si y sunt adiacente in graful G.
Un virf care nu este adiacent cu nici un alt virf al grafului G se numeste virf izolat.
Se numeste lant un sir de virfuri x1,x2, ,xr, cu proprietatea ca oricare doua virfuri vecine sint adiacente, adica (x1,x2), (x2,x3), ,(xr-1,xr) apartin lui E. Daca extremitatile coincid, lantul respectiv se numeste ciclu.
Un graf G se numeste bipartit daca exista o partitie X1 si X2 a virfuri lor din V:
V=X1 U X2 si X1/X2 =
astfel incit oricare muchie (x, y) din E uneste un virf 'x' din X1 cu unul 'y' din X2.
Un graf G se numeste conex daca pentru oricare pereche de virfuri (x, y), cu x si y dinV, x<>y, exista un lant de la x la y.
Se numeste subgraf al unui graf G=(V, E) un graf H=(Y,U), unde Y este inclus in V si muchiile din multimea U sint toate muchiile in E, care au ambele extremitati in Y :
U=
Exemplu
In figura urmatoare se prezinta un graf neorientat:
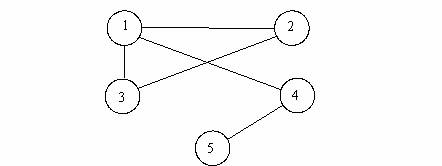
In cazul unui graf orientat, notiunea de muchie se transfrma in notiunea de arc. Putem spune ca pentru un graf neorientat, daca (x, y) este o muchie, atunci in mod necesar si (y, x) este tot o muchie.
Pentru un graf orientat insa, nu exista cale comuna intre doua noduri adiacente pe acelasi arc.
Observatie
Notiunile echivalente pentru lant si ciclu in cazul grafurilor orientate sunt drum respectiv circuit.
Exemplu de graf orientat :
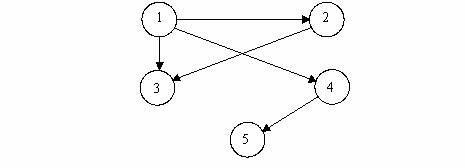
Observatie
Toti arborii studiati in capitolele precedente sunt grafuri orientate aciclice.
Pot fi imaginate mai multe metode (tipuri de date) care sa faca posibila reprezentarea si exploatarea grafurilor in calculator.
In continuare se va prezenta o metoda alternativa de reprezentare a grafurilor folosindu-se matricile. Aceasta metoda de reprezentare are o serie de avantaje cum ar fi usurinta memorarii si manipularii matricilor precum si usurinta de a reprezenta o structura de date de tip graf. Operatiile bine cunoscute in algebra matricilor vor putea fi folosite pentru a se obtine drumuri in graf, cicluri, sau alte caracteristici ale structurii.
Se considera un graf simplu orientat dat de urmatoarea pereche: G=(V,E), unde V este multimea nodurilor, iar E este multimea muchiilor. Desigur, este necesar sa se presupuna un mod de ordonare a nodurilor grafului in sensul ca exista in graf primul nod, al doilea nod, s.a.m.d. Aceasta ordonare este necesara pentru reprezentarea matriciala a grafului G deoarece aceasta reprezentare va depinde de ordonarea datelor nodurilor.
Se va considera o matrice A(NxN) pentru care elementele sunt definite astfel:
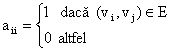
unde prin (vi, vj) s-a notat o muchie intre nodurile vi si vj . Matricea A astfel definita se va numi "matricea de adiacenta" a grafului G. Deoarece fiecare element al acestei matrici este 0 sau 1 ea se mai numeste si matrice binara sau matrice booleana. Se noteaza faptul ca al i-lea rand din matricea de adiacenta este determinat de muchiile care isi au originea in nodul vi deci numarul de elemente egale cu 1 de pe acest rand este egal cu e-gradul nodului vi. Similar, numarul de elemente a caror valoare este egala cu 1 din coloana a j-a este egal cu numarul de arce care intra in nodul vj , deci o matrice de adiacenta defineste complet un graf orientat dat.
Observatie
Un graf simplu orientat se mai numeste si digraf.
Din cele prezentate, rezulta ca o matrice de adiacenta depinde de ordinea elementelor din multimea V. Pentru diferite ordonari ale nodurilor se vor obtine diferite matrici de adiacenta pentru acelasi graf G. Totusi, oricare din matricile de adiacenta obtinute pentru diferite ordonari ale nodurilor, se va putea obtine din alta matrice de adiacenta a aceluiasi graf, prin interschimbari ale unor randuri si coloane corespunzatoare, din matrice.
De fapt, daca pentru doua digrafuri avem matrici de adiacenta care le reprezinta si care se pot obtine una din alta prin interschimbarea unor randuri si coloane corespunzatoare, se va spune ca digrafurile respective sunt echivalente.
Exemplu
Se considera urmatorul digraf in care ordinea nodurilor este cea din figura.
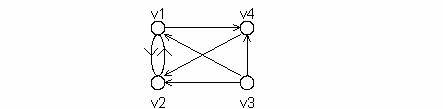
Matricea de adiacenta corespunzatoare digrafului reprezentat in figura este:
|
n1 |
n2 |
n3 |
n4 |
|
|
n1 | ||||
|
n2 | ||||
|
n3 | ||||
|
n4 |
Pornind de la acest graf se poate considera o alta numerotare a nodurilor cu matricea corespunzatoare si se poate arata ca o matrice data se obtine din schimbarea unor randuri si coloane intre ele.
Se poate extinde acum ideea de reprezentare matriceala considerandu-se graful ponderat. Adica, pentru un graf simplu neorientat se ataseaza fiecarei muchii o pondere si elementele matricii de adiacenta vor fi aij=wij , unde wij reprezinta ponderea muchiei (vi , vj) si desigur aij=0 daca (vi , vj) nu exista in graful dat.
Pentru un graf care are numai noduri fara muchii intre ele avem matricea de adiacenta nula. Pentru un graf care are numai bucle proprii pentru fiecare nod (exista o muchie (vi, vi)) si nu are alte muchii, vom avea matricea de adiacenta unitate.
Se vor considera in
continuare puterile matricii de adiacenta pentru un graf dat. Se stie ca un 1
in linia 'i' si coloana 'j', in matricea de adiacenta, semnifica existenta unei
muchii in graf, adica existenta unui drum de lungime 1 in graful dat, de la
nodul vi la nodul vj. Pentru matricea A² elementul ![]() este dat de formula:
este dat de formula:
![]()
adica pentru un 'k'
fixat aikakj=1 daca si numai daca muchiile (vi
, vk), (vk , vj ) apar in graful dat, adica aikakj=1
arata existenta unui drum de la nodul vi la nodul vj de
lungime 2. Deci ![]() este
egal cu numarul de drumuri diferite care au exact lungimea 2 si care sunt intre
nodurile vi si vj. Similar, elementele de pe diagonala
matricii A² date de
este
egal cu numarul de drumuri diferite care au exact lungimea 2 si care sunt intre
nodurile vi si vj. Similar, elementele de pe diagonala
matricii A² date de ![]() arata numarul de cicluri de lungime 2
existente in graful dat care isi au originea si nodul final in nodul vi
. Folosind o argumentatie analoga se obtin semnificatiile pentru elementele
matricilor de adiacenta la diferite puteri.
arata numarul de cicluri de lungime 2
existente in graful dat care isi au originea si nodul final in nodul vi
. Folosind o argumentatie analoga se obtin semnificatiile pentru elementele
matricilor de adiacenta la diferite puteri.
In general se poate face urmatoarea afirmatie: - pentru o matrice A de adiacenta, data pentru un digraf G, elementul din randul 'i' si coloana 'j' a matricii An cu n>1, este egal cu numarul de drumuri de lungime 'n' dintre nodurile vi respectiv vj .
Exemplu
Pentru matricea de adiacenta a grafului din exemplul anterior vom avea urmatoarele puteri:
A2
= 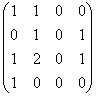 ;
A3 =
;
A3 = 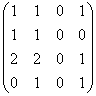 ;
A4 =
;
A4 = 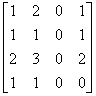
adica avem doua drumuri de lungime 2 intre nodurile v3 si v2 deoarece avem un element egal cu 2 in al 3-lea rand si a 2-a coloana a matricii A², etc.
Se considera un graf G=(V, E) si doua noduri oarecare din graf: vi si vj. Din matricea de adiacenta A se poate determina imediat daca exista o muchie in graful respectiv si cu ajutorul puterilor matricii de adiacenta putem sa vedem numarul de drumuri dintre cele doua noduri date, precum si lungimea acestora.
Se considera acum matricea Br=A+A²++Ar data de suma puterilor matricii de adiacenta. Din matricea Br se poate determina numarul de drumuri a caror lumgime este mai mica sau egala cu 'r' si care exista intre nodurile vi si vj . Deci, daca se doreste sa se determine daca nodul vj poate fi atins din nodul vi este necesar sa se investigheze daca exista un drum de orice lungime intre nodurile vi si vj, adica se va considera matricea de adiacenta cu matricile putere ale ei (metoda care este costisitoare din punct de vedere al timpului de calcul).
Se poate vedea usor ca un digraf simplu cu n noduri are drumuri sau cicluri a caror lungime nu depaseste numarul n. Pentru un drum intre doua noduri se poate considera matricea de adiacenta si puterile ei, dar suntem interesati in determinarea faptului ca exista un drum intre doua noduri vi si vj fara sa examinam toate matricile si puterile lor.
Pentru aceasta se pote calcula matricea Bn in care pentru un element de pe linia i si coloana j se da numarul de drumuri de lungime cel mult egala cu n dintre nodurile vi si vj .
Desigur, in problema atingerii unui nod pornind din alt nod, suntem interesati in existenta drumului si nu ne trebuie lungimea acestuia. Se considera graful G=(V, E) cu n noduri si se considera o matrice P(NxN) care are elementele definite astfel:
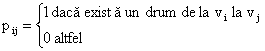
Matricea P se numeste matricea cale a grafului G.
Deci, aceasta matrice va arata existenta sau absenta cel putin a unui drum intre o pereche de noduri date (respectiv existenta sau absenta unui ciclu). In acest sens, matricea de cale nu da o informatie completa a grafului ca in cazul matricii de adiacenta. Matricea de cale poate fi calculata din matricea Bn punand pij=1 daca in matricea Bn in randul 'i' si coloana 'j' avem o valoare diferita de zero.
Exemplu
Considerandu-se graful din primul exemplu se obtine matricea B4 :
B4 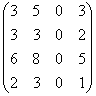 si de aici
matricea P=
si de aici
matricea P=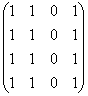
Observatie
Se poate face remarca, ca daca suntem interesati in problema atingerii unui nod din altul esta suficient sa se calculeze Bn-1 (pentru un graf dat cu 'n' noduri) deoarece un drum de lungime n nu poate fi elementar.
Diferenta dintre matricea P calculata din matricea Bn-1 si matricea P calculata din matricea Bn este in elementele diagonalei principale. Se va da o alta metoda de calculare a matricii P care este mai eficienta in practica. Se porneste de la observatia ca nu suntem interesati de numarul de drumuri de diferite lungimi care exista intre doua noduri vi si vj . Aceasta informatie este obtinuta din cauza calcularii puterilor matricii de adiacenta. Pentru calculul diferit al matricii cale se porneste de la observatia ca matricea de adiacenta este o matrice booleana (adica numai cu elemente 1 si 0).
Se considera doua matrici boolene A,
B![]() (NxN).
Notam cu C suma matricilor, C=A
(NxN).
Notam cu C suma matricilor, C=A![]() B,
si cu D produsul matricilor, D=A
B,
si cu D produsul matricilor, D=A![]() B.
Rezulta ca elementele matricilor C si D sunt calculate astfel:
B.
Rezulta ca elementele matricilor C si D sunt calculate astfel:
![]()
![]()
De exemplu, elementul dij
se obtine prin scanarea celui de-al i-lea rand din matricea A de la stanga la
dreapta si, simultan, scanarea celei de-a j-a coloana din matricea B de sus in
jos. Daca pentru un k fixat, al k-lea element din randul matricii A si al k-lea
element din coloana matricii B sunt 1, atunci dij va fi 1. Altfel, dij
va fi zero. Desigur, ca intre matricea de adiacenta si matricea booleana, pe de
o parte, si puterile acestora, pe de alta parte, exista legaturi. Vom nota cu A(2)=A![]() A,
A(3)=A(2)
A,
A(3)=A(2)![]() A,
s.a.m.d. Diferenta dintre puterea a 2-a a matricei de adiacenta si A(2)
este ca A(2) este o matrice booleana si un 1 in randul i
coloana j arata ca exista cel putin un drum intre nodurile vi
, vj pe cand un numar in A² in randul i si coloana j
arata numarul de drumuri de lungime 2 intre cele doua noduri.
A,
s.a.m.d. Diferenta dintre puterea a 2-a a matricei de adiacenta si A(2)
este ca A(2) este o matrice booleana si un 1 in randul i
coloana j arata ca exista cel putin un drum intre nodurile vi
, vj pe cand un numar in A² in randul i si coloana j
arata numarul de drumuri de lungime 2 intre cele doua noduri.
Remarci similare se pot face intre A³ si A(3) s.a.m.d.
Cu aceste descrieri facute, rezulta ca matricea cale poate fi obtinuta din relatia:
![]()
Exemplu
Pentru primul exemplu dat in acest paragraf vom obtine urmatoarele matrici:
A(2)=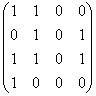 ;
A(3)=
;
A(3)=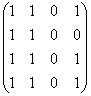
A(4)=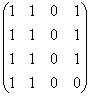 ; P=
; P=
Aceasta metoda de obtinere a matricei de cale se datoreaza lui Warshall care a dat urmatoarea procedura:
** PROCEDURE Warshall(var a,p:matrice;n:integer);
var i,j,k:integer;
BEGIN
p:=a;
![]() for
k:=1 to n do
for
k:=1 to n do
for i:=1 to n do
![]()
![]() for
j:=1 to n do
for
j:=1 to n do
p[i,j]=p[i,j] or p[i,k] and p[k,j]
END;
Se pune acum problema analizei corectitudinii acestui algoritm (adica daca algoritmul produce matricea de cale ceruta).
La primul pas, algoritmul produce o matrice in care elementele pij=1 arata ca exista un drum de lungime 1 de la nodul vi la nodul vj . In continuarea demonstratiei se procedeaza prin inductie matematica.
Presupunem pentru un k fixat ca o matrice intermediara P, produsa de algoritm este astfel incat elementul de pe randul i si coloana j din aceasta matrice este egal cu 1 daca si numai daca exista un drum intre nodurile vi si vj (adica exista un drum intre cele noduri care trece prin nodurile v1 , v2 , ,vk ). Se considera pasul urmator prin actualizarea numarului k. Se va gasi elementul pij=1, fie daca pij=1 de la pasul anterior, fie daca se gaseste un drum intre nodurile vi si vj care trece prin nodurile v1 , v2, , , vk+1 , ceea ce demonstreaza corectitudinea algoritmului.
Se pune acum problema complexitatii algoritmului, adica analiza consumului de timp. Deoarece se considera graful de n noduri si deoarece algoritmul contine trei bucle for incuibate rezulta ca numarul de pasi executati de algoritm este n³. Din punct de vedere al complexitatii spatiale, algoritmul foloseste doua matrici A si P de dimensiune nxn, deci spatiul de memorie ocupat este de ordinul n².
Algoritmul Warshall poate fi
modificat pentru a se obtine o matrice care sa furnizeze lungimea celui mai
scurt drum dintre doua noduri. Pentru aceasta se considera matricea de
adiacenta a unui graf dat. Se inlocuiesc toate elementele zero ale matriciei A
prin infinit (![]() ),
acest lucru aratand ca nu exista nici o muchie intre nodurile considerate.
),
acest lucru aratand ca nu exista nici o muchie intre nodurile considerate.
Urmatorul algoritm va produce matricea cautata, care furnizeaza lungimea drumurilor minime:

Observatie
Semnul '+', din algoritmul de mai sus, indica suma obisnuita a intregilor.
In practica suntem, de fapt, interesati nu numai de lungimea celor mai mici cai dintre doua noduri date ci si de respectiva cale. Se poate modifica simplu algoritmul anterior pentru a se obtine o astfel de cale enumerand nodurile.
2 Reprezentarea grafurilor cu ajutorul listelor
Dezvoltarea structurilor de tip lista pentru reprezentarea grafurilor este un raspuns la cerintele aparute intr-o serie de domenii cum sunt manipularea simbolurilor in teoria algebrica, sau in procesarea textelor. De asemenea, apar probleme care folosesc aceasta implementare a grafurilor in domenii cum sunt inteligenta artificiala, teoria complexitatii calculului, teoria limbajelor si a compilatoarelor.
Manipularea listelor, care reprezinta grafuri, prezinta cateva caracteristici printre care amintim:
1. Necesitati de stocare a informatiei. Cantitatea exacta de memorie necesara stocarii informatiei nu se stie apriori, ci este o caracteristica a procesului executat pentru o problema particulara;
2. Existenta unor operatori specifici. Programele care folosesc astfel de reprezentari de structuri de date contin o serie de functii si proceduri care pot fi proiectate dinainte fiind specifice reprezentarii (vezi operatorii de insertie si de stergere, utilizati frecvent).
Structurile de tip lista, care vor fi discutate, satisfac cele doua criterii de mai sus.
Desigur, prin lista se intelege o secventa finita de zero sau mai multi atomi sau liste. Un atom este un obiect (de exemplu un sir de simboluri) care poate fi distins in lista si tratat ca o structura indivizibila (desigur, atomul poate sa contina mai multe campuri).
Listele pot fi reprezentate cu ajutorul parantezelor in care elementele listei sunt separate prin virgula.
Exemplu
1. (a, (b, c, d), e, (f, g)); 2. ( ); ((a)).
Prima lista contine 4 elemente astfel: un atom - a si un atom e; o lista - (b, c, d), care la randul ei contine 3 atomi - b, c, d si o lista cu 2 atomi - (f, g). A doua lista nu are nici un element, dar lista vida este in cocordanta cu definitia data. Cea de-a treia lista are un singur element care este lista (a), care la randul ei contine un singur element care este atomul 'a'.
Avand in vedere cele discutate putem da urmatoarea reprezentare arborescenta a listelor din exemplu de mai sus, astfel:
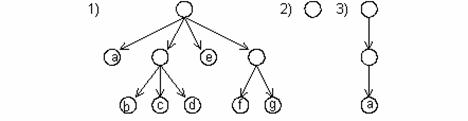
Desigur ca, cea mai adecvata reprezentare este cea inlantuita. Pentru aceasta, fiecare element este indicat printr-o cutie in care avem mai multe campuri. In cazul nostru, fiecare cutie are doua parti. Cea de-a doua parte contine un pointer catre urmatorul element al aceleiasi liste iar prima parte contine, fie un caracter care da numele elementului atomic, fie un pointer catre reprezentarea sub forma de lista, daca avem drept element al listei o sublista. Deci, pentru elemente neatomice vom avea pointeri orizontali pentru elementele aceleiasi liste si pointeri verticali care dau o relatie de ierarhizare intre elementele listei.
Exemplu
Se considera exemplul anterior si vom avea urmatoarea reprezentare de liste inlantuite:
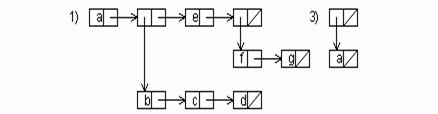
Aceste structuri sunt caracterizate de trei proprietati:
1) Ordinea elementelor - este o relatie definita pe multimea elementelor listei si specifica secventa in care elementele apar in lista, adica in lista (x,y,z) elementul atomic x precede atomul y si atomul z succede atomul y. Desigur, relatia este tranzitiva: x precede y si y precede z rezulta ca x precede z. In reprezentarea cu dreptunghiuri relatia de ordine este definita de sagetile orizontale.
2) Adancimea - este nivelul maxim atribuit unui element arbitrar din lista, sau atribuit unei subliste oarecare din lista. Nivelul unui element este indicat de incuibarea listelor in liste. Daca am avut o reprezentare cu ajutorul parantezelor, nivelul este dat de numarul de perechi de paranteze care inconjoara un element, adica, pentru prima lista din primul exemplu adancimea este 2. In reprezentarea cu ajutorul sagetilor adancimea este data de numarul de sageti verticale care trebuie sa fie urmate in ordine pentru a atinge un element, pornind de la primul element al listei. Daca notam cu d adancimea unui element, atunci, pentru exemplul anterior putem scrie: d(a)=0, d(b)=1. In general, nivelul unui element 'x' este dat de relatia d(x)+1 si adancimea unei liste este valoarea maxima a numarului d, considerat pentru toti atomii listei.
3) Lungimea listei - este data de numarul de elemente care se afla pe primul nivel din lista. De exemplu, pentru lista (a, (b, c), d)) lungimea este
Exista o relatie distincta intre structura de lista si structura de graf orientat fara cicluri. In particular, o lista este un graf orientat cu un singur nod sursa (un nod pentru care i-gradul sau este zero) corespunzator unei intregi liste, iar celelalte noduri sunt conectate la nodul sursa. Fiecare nod, cu exceptia nodului sursa, are i-gradul egal cu 1. Muchiile care parasesc un nod sunt considerate a fi ordonate in reprezentarea cu ajutorul listelor (adica se poate distinge prima muchie, a doua muchie, etc. - care corespund la ordinea elementelor listei).
Desigur ca listele pot contine orice structuri recursive prin incuibari succesive, caz in care anumite liste au o reprezentare finita cu ajutorul parantezelor, dar o reprezentare infinita cu ajutorul grafurilor.
Exemplu
Se considera urmatoarea structura de lista care este reprezentata de urmatorul graf infinit: M=(a, b, M).
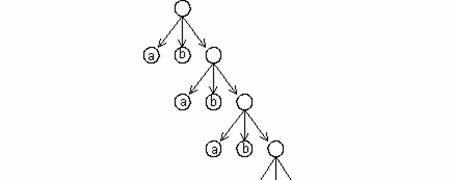
Se pune problema memorarii acestei structuri de tip lista. Desigur, se ia in considerare reprezentarea inlantuita deoarece este mult mai eficienta din punct de vedere al prelucrarii.
Din cele discutate putem sa ne gandim la reprezentarea arborilor binari folosind doua campuri de legatura si un camp care sa contina numele nodului.
Rezulta urmatoarea structura:
![]()
unde DPTR este legatura cu primul element al unei subliste, RPTR este legatura cu urmatorul element din aceasi lista (pe acelasi nivel), iar INFO contine informatia.
Deci un nod atomic este indicat prin DPTR=NULL si INFO contine informatia atomica. Acest format de nod este suficient pentru listele a caror informatie atomica necesita un spatiu mic de memorare. Daca informatia atomica reclama o cantitate relativ mare de memorie se considera drept structura urmatorul format:
![]()
unde RPTR are aceasi semnificatie ca mai sus iar campul atom este de fapt un semafor care permite atasarea elementelor atomice sau elementelor de tip sublista. Daca ATOM=1 inseamna ca nodul este de tip atomic si DPTR este folosit pentru a indica informatia auxiliara atasata nodului respectiv. Daca ATOM=0 atunci DPTR indica catre primul element al unei subliste din structura data.
De exemplu, un nod atomic este de
tipul ![]() , unde
'x' este un pointer catre o structura mare care contine informatia utila
atasata nodului de mai sus.
, unde
'x' este un pointer catre o structura mare care contine informatia utila
atasata nodului de mai sus.
Exemplu
Pentru lista (a, (b, c), d) avem urmatoarea reprezentare:

Pentru a nu incarca figura am facut, in cazul exemplului, urmatoarea schimbare: cand ATOM=1 campul DPTR contine simbolul care noteaza atomul iar cand ATOM=0, campul DPTR contine pointerul catre sublista atasata nodului respectiv.
In cele ce vom discuta se considera ca informatia unui nod atomic este un caracter, dar pentru reprezentarea generala prima conventie este cea indicata a fi utilizata.
In ultima conventie putem reprezenta usor si repetitiile infinite, adica lista M=(a, b, M) si o reprezentare cu cap de lista este data in figura urmatoare:

deci avem o lista circulara si avem nevoie de un pointer care sa indice primul element din lista.
Aceasta reprezentare recursiva a structurii infinite trebuie tratata cu atentie in cazul prelucrarilor pentru a se evita buclele infinite in programele de prelucrare. Desigur ca se poate pune problema spatiului necesar stocarii unei astfel de structuri de date. Putem avea duplicari de cod in cazul in care subliste apar ca elemente la mai multe elemente ale listei date.
Exemplu
Se considera urmatoarea lista (y, (z, w), (z, (z, w), a)) in care sublista (z, w) apare de mai multe ori in structura. Rezulta ca se poate da urmatoarea reprezentare pentru economie de spatiu:
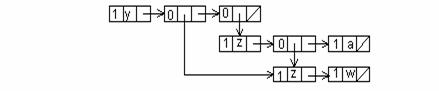
Desigur ca reprezentarile propuse trebuie sa aiba in vedere si eficienta prelucrarilor ulterioare. Pentru exemplul anterior se presupune ca se doreste sa se stearga elementul z din sublista (z, w). In cazul descrierii cu paranteze se obtine urmatoarea lista: (y, (w), (z, (w), a)).
Pentru reprezentarea data cu liste rezulta ca este necesar sa se localizeze elementul 'z' si sa se schimbe doi pointeri care indica acest element. Acest lucru implica mergerea inapoi pe drumul facut pentru gasirea elementului 'z' pentru a localiza si a schimba pointerii respectivi - lucru care este costisitor din punct de vedere al consumului de timp. Deci se pune problema unei structuri care sa prezinte posibilitatea de manipulari eficiente a elementelor structurii.
Din aceste motive se va opta pentru reprezentarea cu cap de lista folosind acelasi format de nod ca inainte. Nodul cap de lista va avea RPTR un pointer catre primul nod al listei, iar DPTR va fi NULL. ATOM=0 pentru capul de lista pentru a indica ca este un nod lista. In aceasta noua conventie lista vida este data de DPTR=RPTR=NULL.
Exemplu
Se considera exemplul anterior si vom avea urmatoarea reprezentare:
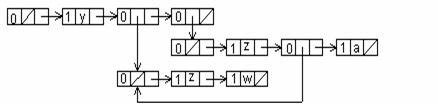
Deci, stergerea elementului z din sublista (z, w) reclama modificarea numai a unui pointer, cel din nodul cap de lista. Procesele de creare, insertie, stergere de elemente dintr-o astfel de structura de lista sunt similare operatiilor echivalente de la arbori.
Se va prezenta pentru inceput operatia de creare a unei structuri de lista pornind de la reprezentarea cu ajutorul parantezelor. Se presupune ca si sirul de caractere de intrare nu contine blocuri, numele unui nod este dat de o singura litera si nu sunt permise listele circulare. Procesul poate fi executat fie iterativ, fie recursiv.
Pasii procesului iterativ sunt urmatorii:
Pas1) Daca primul simbol din sirul de intrare este o paranteza care se deschide atunci se creaza un nod cap, altfel se scrie mesajul lista incorect prezentata si se iese din procedura.
Pas2) Atata timp cat exista simboluri in sirul de intrare se executa urmatorii trei pasi.
Pas3) Daca simbolul curent in sirul de intrare este o paranteza deschisa atunci avem mai multe operatii: se creaza o sublista care se conecteaza la nodul curent, se pune adresa subnodului de sublista intr-o stiva, se creaza un nod cap de lista pentru noua sublista care se ataseaza la nodul sublistei.
Pas4) Daca simbolul curent din sirul de intrare este o paranteza inchisa atunci se termina sublista curenta prin scoaterea celei mai inalte adrese de lista din stiva.
Pas5) Daca simbolul curent este un caracter din multimea caracterelor de la a la z atunci se creaza un nod de lista care se ataseaza la sublista curenta.
Desigur, algoritmul de mai sus, care implementeaza metoda iterativa, va folosi o stiva si se considera ca primeste la intrare un sir de caractere numit INPUT care descrie lista cu ajutorul reprezentarii cu paranteze. Functia CREATE creaza structura de lista corespunzatoare in implementarea cu nod cap de lista. Se foloseste o stiva S ca un vector de pointeri si se folosesc algoritmii elementari PUSH si POP. Variabila CURSOR este folosita pentru a pastra pozitia curenta in sirul de intrare. Se mai folosesc doua variabile temporare de tip pointer, P si Q iar numele nodului este dat de NODE. Desigur ca functia returneaza un pointer catre nodul cap de lista.
Algoritmul este urmatorul:
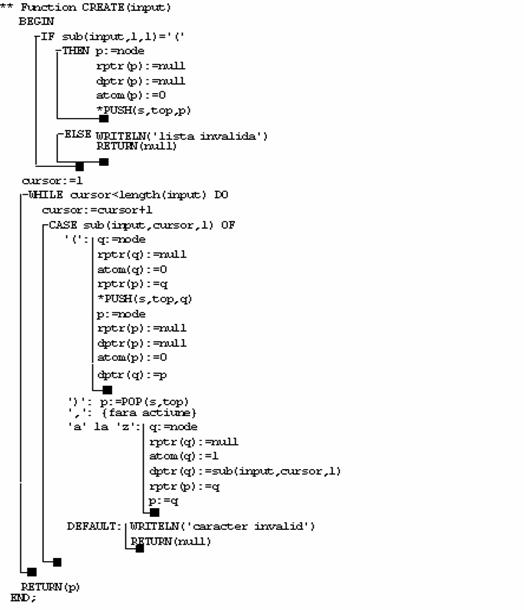
Observatie
Functia de mai sus foloseste o functie SUB(INPUT,i,j) care returneaza o valoare din sirul INPUT care este specificata de parametrii i si j. Parametrul 'i' indica pozitia curenta de unde se extrag simbolurile iar parametrul j specifica lungimea subsirului care se extrage din intrare (in cazul nostru avem un singur caracter, deci j=1).
Implementarea functiilor PUSH si POP este elementara.
Variabila CURSOR in cazul implementarii recursive a procedurii de creare trebuie sa fie variabila globala initializata cu valoarea 1 in afara procedurii recursive. Pentru algoritmul recursiv se da un sir de intrare INPUT care descrie cu paranteze structura de lista a unui graf dat si se va crea o lista cu nod cap. Pointerul p indica nodul cap al listei create si este initializat in afara procedurii. CURSOR este o variabila cu aceeasi semnificatie. Se foloseste o variabila temporara q de tip pointer. Implementarea procedurii recursive este urmatoarea:

Urmatoarea operatie este aceea de Despicare a unei liste, care genereaza doua liste dintr-o lista data. Pentru implementarea acestei operatii este nevoie sa se introduca doua entitati logice si anume cap si urma pentru o lista data.
Exemplu
Se considera lista ((a, b), c, (d, e)) care este descrisa de urmatoarea structura:
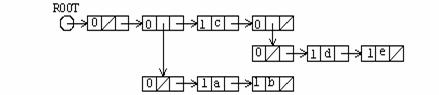
Pornind de la descrierea cu paranteze avem sublista cap (a, b) si sublista coada (c, (d, e)). Considerand reprezentarea cu dreptunghiuri vom avea urmatoarea descriere pentru cele doua entitati logice:
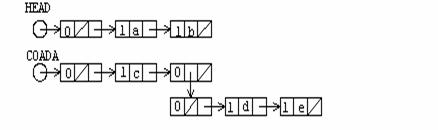
Se noteaza acum efectul operatiei de despicare asupra nivelului elementelor listelor rezultate. Elementele listei cap au nivelul lor redus cu o unitate in timp ce nivelul elementelor din lista coada ramane nealterat. Algoritmul care returneaza un pointer catre lista cap primeste pointerul ROOT catre capul structurii de lista initiala. Algoritmul este urmatorul:

Dandu-se pointerul ROOT catre nodul cap al structurii de lista initiala, functia TAIL va crea un nod cap de lista si returneaza adresa lui, iar campul RPTR al acestui nod cap de lista indica catre lista coada. Sunt utilizate doua variabile, p si q temporare, de tip pointer.

Operatia care are efectul invers operatiei de despicare a unei liste este aceea de cuplare (alaturarea listei cap si listei coada) realizata de algoritmul CONSTRUCT.
Dandu-se doi operanzi, primul putand sa fie un atom, sau o lista, cel de-al doilea fiind o lista, operatia creaza o structura de tip lista folosind primul argument drept lista cap si cel de-al doilea argument drept lista coada.
Exemplu
Se considera A ca fiind lista (q) si B ca fiind lista (d, e). Atunci, legarea celor doua liste conduce la lista ((q), d, e). Daca A este atomul s iar B este lista (t, u) alaturarea conduce la lista (s, t, u).
Se noteaza faptul ca nivelul fiecarui element din primul argument creste cu o unitate ca rezultat al acestei operatii, in timp ce nivelul elementelor celui de-al doilea argument ramane neschimbat.
Observatie
Operatia de alaturare a doua structuri logice este invalida in cazul in care cel de-al doilea argument nu este o lista (desi poate fi lista vida).
Exemplu
A este atomul x iar B este lista vida ( ). Alaturarea lor conduce la lista (x).
In urmatorul algoritm se presupune ca A este un atom. El este reprezentat de un nod cu campul DPTR indicand catre informatie si campul RPTR=NULL. Nodul cap de lista pentru lista B devine nod cap de lista pentru noua structura de lista. Pentru algoritm se considera drept prim argument A un pointer catre capul de lista al structurii de liste, sau catre un atom, iar cel de-al doilea argument B drept un pointer catre nodul cap de lista al unei structuri liste. Se va crea o lista L astfel incat vom avea HEAD(L)=A si TAIL(L)=B. De asemenea, se vor folosi doua variabile pointer ajutatoare, p si q.
Algoritmul este descris de urmatoarea procedura:

O alta operatie familiara manipularii structurilor de tip lista este aceea a concatenarii a doua structuri, operatia fiind realizata de algoritmul APPEND.
Exemplu
Daca A este lista (a, (b,c)) si B este lista (d, f) atunci concatenarea lor conduce la lista (a, (b,c),d,f).
In urma operatiei de concatenare, nivelul fiecarui element din ambele liste ramane acelasi. De asemenea, cele doua argumente A si B nu pot sa fie atomi. Considerand reprezentarea cu ajutorul dreptunghiurilor, operatia este urmatoarea:
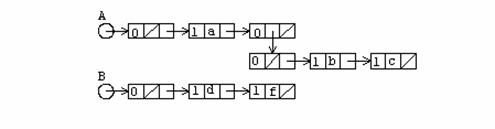

Se observa ca elementele listei A preced elementele listei B si nodul cap de lista pentru lista A devine nod cap de lista pentru noua structura. Deoarece, pointerul A este alterat de catre algoritm se presupune ca el este pasat prin referinta algoritmului.
Avem urmatoarea descriere a algoritmului:

O alta operatie utila in cazul mai multor structuri de tip lista ca mai sus este cea a enumerarii atomilor unei liste date.
Exemplu
Lista (a,b,(c,d)) are 4 atomi in timp ce lista (( )) nu are nici un atom.
Procedura de enumarare poate fi iterativa sau recursiva si se va prezenta varianta recursiva. Procedura se apeleaza recursiv pana cand se indeplineste conditia RPTR=NULL.
Se considera data o lista A in care parametrul A este un pointer catre nodul cap de lista. Varianta recursiva calculeaza numarul de atomi din lista A si returneaza rezultatul in variabila COUNT. Desigur, variabila COUNT este initializata cu zero in afara procedurii.
Algoritmul este urmatorul:

Urmatorul algoritm implementeaza operatia de stergere a unui nod atomic care contine anumite informatii. Se presupune ca structura initiala de lista nu contine subliste recursive si se presupune ca exista numai o copie a informatiei nodului, cu toate ca pot sa existe mai multi pointeri care sa indice aceeasi pozitie in structura auxiliara de memorie.
Exemplu
Se considera a nodul ce se doreste sters din lista (b,a,(a)), atunci in urma stergerii rezulta structura (b,( )).
Din acest exemplu rezulta ca stergerea unui nod dintr-o lista nu conduce la disparitia listei. Algoritmul poate fi implementat iterativ sau recursiv, si se va prezenta doar formularea recursiva.
Se considera ca se da un pointer remove la numele nodului de lista ce urmeaza a fi sters. Varianta recursiva sterge toate aparitiile acestui nod din structura data.
Algoritmul este initial apelat cu un pointer q care indica nodul cap de lista si un pointer p asignat cu valoarea RPTR a acestui pointer:

Observatie
Structura de tip lista prezentata mai sus este mai complexa decat structurile de tip arbore, de exemplu, si din acest motiv distrugerea unei liste este o operatie mult mai complexa decat stergerea, de exemplu, a unui arbore. Astfel, o lista poate sa fie continuta ca sublista in mai multe subliste de nivel inferior, deci pot sa existe mai multe referinte catre lista respectiva.
In continuare se prezinta implementarile algoritmilor din acest paragraf in limbajul C.
Primul program prezinta implementarea algoritmului de creare a unei structuri de tip lista pornind de la reprezentarea cu ajutorul parantezelor.
#include <stdio.h>
/* structura zz implementeaza tipul lista generalizata;*/
typedef struct zz
dptr;
} node, *pnode;
/* structura yy implementeaza o stiva folosita in algoritmul
de constructie */
typedef struct yy stack,*pstack;
char SUB(char *str,int start)
void PUSH(pstack *TOP,pnode element)
pnode POP(pstack *TOP)
pnode CREATE(char *INPUT)
else
cursor=0;
while(cursor < strlen(INPUT)-1)
else
break;
}
}
return(p);
void print_list(pnode rad,int nivel)
else
print_list(p->dptr.pointer,nivel+1);
return;
void main()
Urmatorele functii implementeaza crearea unei liste generalizate folosind o functie recursiva si implementeaza toate celelalte routine prezentate mai sus in pseudocod.
#include <stdio.h>
typedef struct zz
dptr;
} node, *pnode;
int cursor, call;
char SUB(char *str,int start)
void RECCREATE(char *INPUT,pnode p)
else
break;
}
}
return;
void print_list(pnode rad,int nivel)
else
print_list(p->dptr.pointer,nivel+1);
return;
void HEAD(pnode ROOT,int *atom,char *ch,pnode *ref)
p=ROOT->rptr;
if(p==NULL)
if(p->atom)
else
return;
void TAIL(pnode ROOT,pnode *ref)
p=ROOT->rptr;
if(p==NULL)
q=(pnode)malloc(sizeof(node));
q->atom=0;
q->dptr.pointer=NULL;
q->rptr=p->rptr;
*ref=q;
return;
void CONSTRUCT(pnode A,pnode B)
if(B->dptr.pointer!=NULL)
if(A->atom==1)
else
return;
void APPEND(pnode A,pnode B)
if(B==NULL || B->dptr.pointer!=NULL)
while(A->rptr!=NULL)
A=A->rptr;
A->rptr=B->rptr;
free(B);
return;
void COUNTER(pnode A, int *COUNT)
void DELETE(pnode REMOVE, pnode Q, pnode P)
else
return;
Observatie
Utilizarea acestor functii depinde de aplicatie si este lasata la latitudinea cititorului.
Totusi, in cei mai multi algoritmi de prelucrare a grafurilor se considera reprezentarea acestora prin liste de adiacenta.
Se presupune data o lista 'verticala' cu toate nodurile grafului, iar fiecare nod al listei verticale contine headerul (capul) unei alte liste 'orizontale' cu nodurile adiacente nodului curent din lista 'verticala'.
Se considera urmatorul graf:
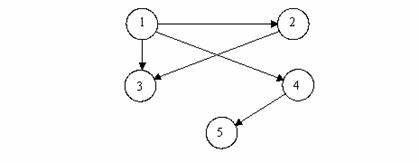
Pentru graful din exemplu avem urmatoarea reprezentare prin liste de adiacenta:
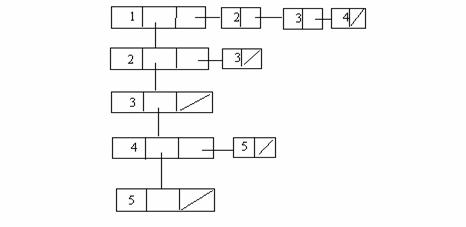
Acest mod de reprezentare are avantajul utilizarii unui spatiu de memorie mai mic, in comparatie cu reprezentarea anterioara, dar timpul de lucru cu aceasta structura este mai mare (accesul la un element al uneia din liste se face numai secvential).
In acest caz se pot folosi urmatoarele tipuri de date.
typedef struct tadj
TADJ;
typedef struct tgraph
TGRAPH;
3 Operatii asupra grafurilor
Aplicatiile cu structuri de tip graf, in general, utilizeaza urmatoarele operatii primitive sau combinatii ale acestora:
1. Crearea grafului;
2. Cautarea unui virf ;
Inserarea unui virf;
4. Eliminarea unui virf;
5. Parcurgerea grafului (DEPTH-FIRST, BREADTH-FIRST, DEPTH);
6. Gasirea arcului catre primul virf adiacent;
7. Gasirea arcului catre urmatorul virf adiacent;
8. Gasirea arcului intre doua virfuri date;
Crearea grafului
Algoritmul folosit pentru crearea grafului presupune urmatorii pasi:
Pas1) se citeste numarul de noduri;
Pas2) pentru fiecare nod:
- se citeste cheia;
- se initializeaza cimpul 'visit';
- se construieste lista de adiacenta;
Primul nod care se va citi va reprezenta capul listei nodurilor grafului si se numeste virful grafului. Acesta este memorat in variabila globala 'rad' si reprezinta nodul 'sursa'.
Se observa ca scrierea unei proceduri de creare a unui graf depinde de modul cum sunt structurate datele de intrare.
TGRAPH *creare()
while(n<0);
dimgraph=sizeof(TGRAPH);
for (i=1;i<=n;i++) /* se creaza lista de headere */
pg->list=pl1;
}
return rad;
}
Cautarea unui virf
Cautarea virfului se face dupa cheia de identificare a virfului respectiv. Procesul se realizeaza cautind cheia specificata in 'lista verticala' a elementelelor grafului.
Functia 'cauta' intoarce valoarea adresei de memorie a elementului din lista. In cazul in care in lista nu exista nici un virf cu cheia specificata valoarea returnata este NULL.
TGRAPH *cauta(TGRAPH *p,int k)
return p;
}
Inserarea unui virf
Virful care va fi adaugat va fi specificat prin cheia sa de identificare.
Algoritmul propus consta in urmatorii pasi:
Pas1) daca virful nu este in graf si daca graful nu e vid :
- se insereaza virful la sfirsitul listei de headere;
- se citeste lista nodurilor adiacente;
- se actualizeaza celelalte liste de adiacenta;
Pas2) altfel
- daca graful este vid:
- se creaza lista de headere cu nodul specificat;
- virful grafului indica virful nou introdus;
- altfel se semnaleaza prezenta virfului in graf;
TGRAPH *insert(TGRAPH *rad,int k)
};
pg1->list=pl1;
}
else
printf ('Nodul deja este in graf');
return rad;
Gasirea arcului catre primul varf adiacent:
Functia propusa furnizeaza primul nod din lista de adiacenta corespunzaroare nodului cu cheia 'k'.
Se returneaza valoarea 0 in urmatoarele doua situatii:
- nu s-a gasit nodul cu cheia 'k' in lista de headere;
- lista de adiacenta corespunzatoare este vida;
int virfadiac(TGRAPH *rad, int k)
Gasirea arcului catre urmatorul varf adiacent:
Functia 'urmvfadiac' primeste un arc, verifica apartenenta acestuia la graf si in caz ca acesta apartine grafului, returneaza urmatorul nod adiacent al lui k1 (adica succesorul lui k2 din lista de adiacenta corespunzatoare lui k1).
Se returneaza valoarea 0 in urmatoarele trei cazuri :
- nu s-a gasit nodul k1 in lista de headere
- nu s-a gasit nodul k2 in lista de adiacenta a lui k1
- nu exista succesor in lista de adiacenta pentru k1
int urmvfadiac (TGRAPH *rad, int k1,int k2)
if ((p->key == k1) && (pl->key == k2) && (pl->next != NULL))
return (pl->next->key);
else
return(0);
}
Gasirea arcului intre doua varfuri date:
Functia primeste doua chei ( k1, k2 ) si verifica daca acestea pot fi un arc al grafului.
Valoarea 1, este returnata in caz afirmativ, iar 0 in urmatoarele cazuri :
- nu este gasita cheia k1 in lista de headere
- nu este gasita cheia k2 in lista de adiacenta a lui k1
int arck (TGRAPH *rad , int k1,int k2)
if ((p->key == k1) && (pl->key == k2))
return 1;
else
return 0;
}
Eliminarea unui varf
Virful care trebuie eliminat se specifica prin cheia sa de identificare.
O varianta de algoritm care realizeaza eliminarea unui virf dintr-un graf este urmatoarea:
Pas1) daca varful este in graf:
- se elimina virful din lista 'verticala';
- se actualizeaza listele de adiacenta;
- se elibereaza memoria ocupata de nod si lista sa
Pas2) - altfel se semnaleaza absenta nodului
TGRAPH *
/* se izoleaza nodul in lista */
pl=pg->list; /* de headere */
while (pl != NULL)
if (gasit == 1)
}
pl3=pl; /* se elibereaza spatiul alocat */
pl=pl->next;
free(pl3);
free(pg);
}
return rad;
}
Aplicatie
Pentru a se observa mai clar modul in care lucreaza algoritmii prezentati mai sus, se propune o procedura de afisare a unui graf.
Se utilizeaza reprezentarea grafului pin liste, iar procedura este functionala in contextul tipurilor de date definite anterior.
Se plaseaza nodurile in virfurile unui poligon regulat, apoi prin parcurgerea listelor de adiacenta se traseaza arcele intre noduri. Calculul pozitiei pe display se realizeaza cu o procedura exterioara 'coord', iar pentru a se stabili o corespondenta intre cheia de identificare a unui virf si numarul sau in graf se foloseste procedura 'nrord'.
Algoritmul folosit este util numai pentru seturi de date experimentale, el neasigurind incadrarea completa pe ecranul display-ului a grafului. Acest lucru se realizeaza explicit prin specificarea laturii poligonului. Se recomanda pentru un numar de virfuri in intervalul [4..12] cu l=140).
void coord(int k,int *x,int *y)
int number(TGRAPH *rad,int k)
return i;
}
void poligon(TGRAPH *rad,int l)
alfa=PI/n;
r=(int)(l/2/sin(alfa));
pg=rad;
while (pg != NULL)
while (pl != NULL)
pg=pg->next;
}
}
Se considera acum un program simplu in care se va utiliza procedura descrisa mai sus.
Programul creaza un graf (utilizind procedura 'creare') si il afisaza pe display.
#include <stdio.h>
#include <conio.h>
#include <alloc.h>
#include <math.h>
#include <graphics.h>
#include <process.h>
#include <stdlib.h>
#define PI 1415
typedef struct tadj
TADJ;
typedef struct tgraph
TGRAPH;
TGRAPH *rad;
float alfa;
int r;
int x0,y0;
int gdriver = DETECT, gmode, errorcode;
TGRAPH *rad;
TGRAPH *creare()
void coord(int k,int *x,int *y)
int number(TGRAPH *rad,int k)
void poligon(TGRAPH *rad,int l)
void main()
poligon(rad,160);
do while (! kbhit());
closegraph();
}
Observatie
EGAVGA.BGI trebuie sa se afle in directorul curent.
Parcurgerea grafurilor
Algoritmul DEPTH-FIRST
Algoritmul Depth-First parcurge graful mergind cit mai in adincime pe arcul spre primul nod vecin nevizitat al nodului curent. In cazul in care nu mai exista un nod vecin nevizitat, se revine la nodul anterior, se cauta un primul nod nod nevizitat s.a.m.d.
Nodurile care au fost vizitate sint memorate intr-o stiva care, dupa cum s-a observat, este necesara pentru asigurarea reluarii parcurgerii in adincime in cazul blocarii intr-un nod.
Nodurile care nu mai au vecini nevizitati sint eliminate din stiva; parcurgerea terminindu-se cind stiva este vida.
Secventa de chei generata de parcurgerea Depth-First pentru graful neorientat din figura urmatoare este : 1,2,5,3,7,6,4,8.
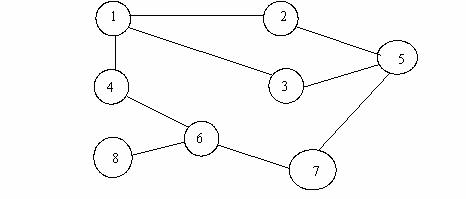
Se observa ca in momentul in care un virf 'j' este introdus in stiva, el ramine acolo pina cind sint vizitate toate virfurile la care se poate ajunge plecind din el, si care nu au aparut in stiva inainte de introducerea lui 'j'.
Datorita modului de definire, algoritmul poate fi usor implementat recursiv.
Pseudocod :
| * procedura DFS( p );
|
| p.visit <- 1 ;
| |daca(* exista w adiacent cu p astfel incat w.visit=0 )
| | atunci
| | * executa DFS (w);
| |_#
|____#
Implementarea algoritmului in C este urmatoarea:
void dfs(TGRAPH *v)
pl=v->list;
while (pl != NULL)
pl=pl->next;
Pentru grafurile orientate exista posibilitatea ca procedura 'dfs' prezentata mai sus sa nu viziteze toate nodurile grafului. In acest caz trebuie ales un nou punct de pornire pentru 'dfs' dintre nodurile grafului ramase nevizitate.
Procedura 'dft' realizeaza acest lucru parcurgind lista de headere dupa sfirsitul primului apel 'dfs', pina la gasirea unui nod nevizitat. Se apeleaza 'dfs' din acest loc, iar tot de aici se va parcurge si lista pina la urmatorul nod nevizitat, dupa sfirsitul apelului.
Se repeta strategia de mai sus pina se ajunge la sfirsitul listei de headere.
Observatie
Pentru cazul particular al arborilor metoda corespunde vizitarii in preordine a nodurilor.
In cazul grafului orientat din exemplu aplicarea acestui algoritm conduce la urmatoarea secventa de chei: 1,2,5,3,7,6,4,8.
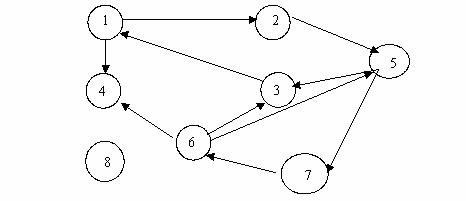
Pseudocod:
| * procedura DFT ( rad ) este :
|
| | pentru (* fiecare nod w ramas nevizitat ) executa :
| | DFS ( w );
| |_#
|_____#
Implementarea in limbajul C este urmatoarea:
void dft(TGRAPH *rad)
u=rad;
while (u != NULL)
u=u->next; /* se alege alt nod de pornire */
}
}
Algoritmul BREADTH-FIRST
Metoda Breadth-First evolueaza in latime, in jurul punctului de pornire in sensul ca se viziteaza nodul curent, apoi vecinii acestuia, apoi vecinii inca nevizitati ai acestora s.a.m.d.
Se foloseste o coada pentru memorarea nodurilor adiacente nodului curent. Nodurile aflate la un moment dat in coada sint nevizitate, din acest motiv, algoritmul trebuie sa impiedice introducerea de mai multe ori in coada a aceluiasi nod.
In analogie cu metoda prezentata anterior algoritmul se termina in momentul cind coada este vida.
Secventa de chei rezultata in urma parcugerii prin aceasta metoda a grafului prezentat in exemplul anterior este : 1,2,3,4,5,6,7,8.
Tipul cozii si operatiile cu ea, nesesare in implementarea metodei Breadth-First sint prezentate mai jos.
Observatie
Pointerii 'pf' si 'pr' indica primul respectiv ultimul nod ale cozii, iar in program trebuiesc declarati ca variabile globale.
typedef struct tqueue
TQUEUE;
void push(TGRAPH *v)
TGRAPH *pop(void)
else
return (NULL);
Putem trece acum la prezentarea implementarilor metodei Breadth-First de parcurgere a grafurilor.
Pseudocod :
| *procedura BFS (p)
| | pentru j=1,n executa
| | p.visit <- 0;
| |_#
| p.visit <- 1;
| q <- p ;
| *initializeaza coada C cu elemente adiacente lui q
| | cit timp ( * coada C nu e vida ) executa
| | | pentru ( toti k vecini ai lui q ) executa
| | | | daca k.visit <> 0 atunci
| | | | * introdu k in C;
| | | | k.visit <- 1;
| | | |_#
| | |____#
| | * extrage q din coada C;
| |________#
|___#
Implementarea in limbajul C este urmatoarea:
void bfs(TGRAPH *rad,TGRAPH *v)
pf=NULL;
pr=NULL; /* initializare coada */
u=v;
v->visit=1;
printf('%d ',u->key);
while (u != NULL)
pl=pl->next;
};
u=pop(); /* se furnizeaza un nod din coada */
}
printf('n');
}
Pentru grafurile orientate se poate intimpla ca Breadth-First sa nu asigure vizitarea tuturor nodurilor grafului. In acest caz trabuie gasit un nou punct de pornire pentru Breadth-First (ales dintre nodurile ramase nevizitate).
Pentru graful orientat din exemplul anterior parcurgerea in latime genereaza urmatoarea secventa de chei :1,2,4,5,3,7,6,8.
Observatie
In cazul particular al unui arbore metoda Breadth-First corespunde vizitarii radacinii, apoi, succesiv nodurile de pe fiecare nivel.
Procedura care realizeaza parcurgerea Breadth-First pentru un graf orientat este prezentata in continuare.
Pseudocod :
| * procedura BFT (rad) este
| * executa BFS(rad);
| | pentru ( *fiecare nod q ramas nevizitat ) executa
| | BFS (q) ;
| |_#
|____#
void bft(TGRAPH *rad)
pf=NULL;
pr=NULL;
u=rad;
while (u != NULL)
/* se alege un nou nod pt bfs */
Algoritmul DEPTH
Daca inlocuim coada, din algoritmul de parcurgere Breadth-First, cu o stiva se obtine metoda Depth de parcurgere a grafurilor.
Pentru graful neorientat din exemplul anterior parcurgerea Depth genereaza urmatoarea secventa de chei : 1,2,3,4,6,7,8,5.
Se propun urmatorul tip de date si doua proceduri de exploatare a unei stive, pentru a se putea urmari cum functioneaza metoda Depth.
typedef struct tstack
TSTACK;
void pushst(TGRAPH *v)
TGRAPH *popst(void)
else
else
return (NULL);
}
Conversii intre cele doua moduri de reprezentare
Dupa cum s-a specificat intr-un paragraf anterior se pot construi tipuri de date care sa permita exploatarea cit mai avantajoasa a structurii de tip graf, necesara intr-o situatie particulara. Analog, diverse module ale unui program, sint proiectate ca sa lucreze cu moduri diferite de reprezentare ale unei aceleiasi structuri de date. In acest caz, pentru a asigura compatibilitatea datelor prin care comunica un modul cu altul este necesara convertirea lor in modul de reprezentare in care este proiectat modulul ce le receptioneaza.
Pentru exemplificare, se vor prezenta doua proceduri care realizeaza o corespondenta biunivoca intre cele doua moduri de reprezentare a unui graf, prezentate anterior.
[a] Conversia din reprezentarea dinamica in cea statica
Procedura care realizeaza acest lucru va construi o matrice de adiacenta pornind de la reprezentarea prin liste de adiacenta.
Algoritmul este:
- se calculeaza dimensiunea matricii si se introduc in linia si coloana 0 cheile nodurilor
- se initializeza matricea cu elementul 0 (graful vid)
- parcurgind fiecare lista succesiv se identifica arcele grafului si se inlocuiesc corespunzator in matrice cu elementul 1.
MADC *convertGM(TGRAPH *rad)
for (i=1;i<=nm;i++)
for (j=1;j<=nm;j++)
(*A).mat[i][j]=0;
(*A).mat[0][0]=0;
(*A).n=nm;
p=rad;
i=0;
while (p != NULL)
p=p->next;
return A;
}
[b] Conversia din reprezentarea statica in cea dinamica
Se porneste de la matrice de adiacenta . Stiind ca, daca A(i,j)=1, inseamna ca nodul corespunzator lui 'j' se va afla in lista de adiacenta corespunzatoare lui 'i'.
Cu aceasta observatie conversia din forma de reprezentare statica in cea dinamica se va face urmind urmatorii pasi:
- se parcurge intreaga matrice, si pentru fiecare A(i,j)=1:
- se identifica nodul corespunzator lui 'i' ( A(0,i) )
- se insereaza nodul in lista de headere
- se identifica nodul corespunzator lui 'j' ( A(0,j) )
- se insereaza nodul in lista de adiacenta
TGRAPH *convertMG(MADC A)
pg->list=pl1;
}
return rad;
}
Aplicatie
Se propune ca aplicatie o exemplificare a unei 'parcurgeri neimpuse' a unui graf.
O parcurgere neimpusa, asa cum sugereaza si numele nu presupune parcurgerea integrala a grafului (vizitarea tuturor nodurilor cu algoritmii prezentati mai sus, sau adaptari ale acestora), ci doar a unei secvente de virfuri care satisfac un anumit criteriu stabilit de utilizator.
O astfel de parcurgere construieste un subgraf implicit al grafului initial, ale carui virfuri satisfac criteriul stabilit. Construirea subgrafului se face identificand drumuri in graf care corespund criteriului.
Pseudocodul acestui algoritm este urmatorul :
| * procedura SELECT (graf) este:
| * initializarea grafului;
| | cit timp ( * exista noduri care satisfac criteriul) executa
| | * alege p conform criteriului;
| | * prelucreaza p;
| | p.visit <- 1;
| | | cit timp (* exista cale in graf pt. criteriu) executa
| | | * alege pl conform criteriului;
| | | * identifica nodul p corespunzator lui pl;
| | | p.visit <- 1;
| | |__#
| |________#
|______________#
Criteriul stabilit pentru procedura implementata este dat de conditia ca nodurile afisate sa aiba cheile intr-un interval [a..b].
# include <stdio.h>
# include <conio.h>
# include <alloc.h>
# include <stdlib.h>
typedef struct tadj
TADJ;
typedef struct tgraph
TGRAPH;
TGRAPH *rad;
TGRAPH *creare()
TGRAPH *cauta(TGRAPH *p,int k)
void select(TGRAPH *rad,int a,int b)
;
p =rad;
while (p != NULL)
else pl =pl->next;
};
};
};
if (p != NULL) p =p->next;
};
}
void main()
Probleme propuse
1. Realizati singuri un program care sa permita explorarea unui graf (inserare, stergere, cautare, etc.) utilizind procedurile si functiile prezentate in paragraf.
2. Pentru a putea reface structura initiala a unui graf, dupa efectuarea unor operatii asupra lui, se vor memora intr-o lista ordinea operatiilor care modifica efectiv graful (stergere, inserare) si cheile asupra carora se efectueaza operatiile respective.
Refacerea grafului se realizeaza parcurgind lista in sens invers si realizarea la fiecare pas a operatiei complementare celei continute in lista. Realizati un program care sa efectueze operatia de refacere a grafului initial.
Sa se realizeze o procedura care sa elimine acele virfuri care apar de mai multe ori in graf.
4. Sa se scrie un program care sa insereze intr-un graf acele virfuri astfel incit cheile grafului obtinut sa formeze un sir continuu de valori ( De exemplu, se porneste de la secventa 1,3,4,6 si dupa inserarea cheilor 2,5,6 sa se obtina 1,2,3,4,5,6 ).
5. Se da o padure de arbori binari. Se cere procedura de creare a unui graf care sa contina toate nodurile padurii, o singura data iar arborii binari din padure sa fie subgrafuri ai grafului rezultat.
6. Matricea de adiacenta a unui graf poate fi reprezentata ca o matrice rara cu ajutorul listelor. Propuneti un tip de date pentru reprezentarea unei astfel de matrici rare si rescrieti functiile prezentate in lucrare pentru o astfel de reprezentare.
7. Fiind date doua grafuri, sa se scrie o procedura care sa creeze un nou graf astfel incit grafurile initiale sa fie subgrafuri ale grafului rezultat.
8 Fiind date doua grafuri, sa se scrie o procedura care sa creeze un graf care sa contina nodurile comune celor doua grafuri, iar graful rezultat sa fie sugraf al celor doua grafuri initiale.
9. Sa se scrie procedurile pentru parcurgerea grafurilor folosind reprezentarea prin matrici de adiacenta.
10. Sa se propuna o modalitate de reprezentare a unui graf tratind matricea de adiacenta ca o matrice rara.
Sa se scrie procedura pentru conversia acestei structuri in structura de reprezentare a grafului prin liste de adiacenta.
11. Utilizind algoritmul de 'parcurgere neimpusa' sa se implementeze programe pentru urmatoarele criterii :
- nodurile care contin chei numere pare
- nodurile care contin chei numere prime.
- nodurile sa formeze o progresie de ratie data.
12. Sa se scrie o procedura care determina daca un graf neorientat este conex (tare conex) si care determina toate componentele conexe (tare conexe) ale grafului.
1 Sa se scrie o procedura care determina toate componentele ciclice ale unui graf.
14. Utilizind strategia Breadth-First sa se gaseasca cel mai lung drum intr-un arbore .
15. Se considera un arbore A. Un virf 'v' al lui A se numeste termi nal, daca exista o singura muchie in A care este incidenta in v.
Sa se conceapa si sa se implementeze un algoritm care sa determine toate virfurile terminale ale lui A.
16. Sa se scrie o procedura care listeaza in ordine descrescatoare toate caile din graf dintre doua virfuri date in ordinea descrescatoare a lungimii lor (utilizati o structura de date adecvata pentru memorarea si sortarea cailor).
18. Se considera un labirint reprezentat ca un graf orientat. Utilizati Depth-First pentru gasirea unui drum in labirint.
19. Se numeste graf pe mai multe nivele un graf orientat G=(V,E) in care :
- virfurile sint asezate pe 'n' nivele numerotate de la 1 la n.
Fie Vi multimea virfurilor de pe nivelul i:
- pentru orice arc (i,j) exista indicele 'k' in multimea astfel ca: 'i' apartine lui Vk si 'j' apartine lui Vk+1.
- exista un singur virf pe nivelul 1 (notat cu S) si un singur virf pe nivelul 'n' (notat cu T);
- fiecarui arc i se asociaza un cost Cij;
Se cere:
a) sa se proiecteze o structura de date pentru reprezentarea unui graf multinivel;
b) sa se determine un drum de cost minim intr-un graf multinivel (costul unui drum fiind suma costurilor arcelor din care este format) de la virful initial S la virful final T.
4 Sortare Topologica
In acest paragraf se va prezenta utilizarea algoritmului de parcurgere in adancime pentru a executa o sortare topologica a nodurilor unui graf orientat aciclic (un astfel de graf se mai numeste DAG). O sortare topologica pentru un graf orientat aciclic, G=(V,E) este o ordonare liniara a tuturor muchiilor lui astfel incat daca G contine o muchie (u,v) atunci nodul 'u' apare inaintea nodului 'v' in ordonarea facuta (daca graful nu este aciclic atunci nici o ordonare liniara nu este posibila). O sortare topologica a unui graf poate fi privita si ca o ordonare de-a lungul unei linii orizontale a nodurilor sale, astfel incat toate muchiile orientate pornesc de la stanga spre dreapta. Din acest motiv sortarea topologica este diferita de tipurile uzuale ale algoritmilor de sortare. Grafurile orientate aciclice sunt folosite in multe aplicatii in care este importanta ordinea de executie a evenimentelor.
Pentru implementarea algoritmului de sortare topologica se va utiliza algoritmul de parcurgere in adancime prezentat in [10], de unde se vor utiliza si unele exemple. Astfel nodurile vor fi colorate in procesul de parcurgere pentru a se indica starea in care se afla. Fiecare nod este initial alb, apoi devine gri cand este descoperit in procesul de parcurgere si devine negru cand se termina prelucrarea lui (adica atunci cand lista de adiacenta a nodurilor lui a fost complet examinata).
Aceasta tehnica garanteaza faptul ca fiecare nod este depus o singura data intr-un arbore in adancime astfel incat arborii padurii sunt disjuncti. Pe langa crearea padurii in adancime, metoda procedeaza la o 'stampilare de timp' a fiecarui nod, adica fiecare nod 'v' are doua stampile de timp. Prima inregistreaza marimea d(v) care reprezinta momentul la care a fost descoperit pentru prima data nodul (moment in care el devine gri), iar cea de-a doua stampila de timp, notata f(v), inregistreaza momentul cand se termina de examinat lista de adiacenta a nodului 'v' (adica momentul cand el este colorat in negru).
Aceste stampile de timp sunt folosite in multi algoritmi care prelucreaza grafuri si sunt folositoare pentru caracterizarea comportarii algoritmilor (inclusiv a metodelor de parcurgere in adancime). Aceste stampile de timp sunt de fapt numere intregi cuprinse intre 1 si 2|V|, deoarece exista un singur eveniment (moment) al descoperirii nodului si un singur eveniment (moment) al terminarii prelucrarii nodului, pentru fiecare nod din multimea V.
Pentru fiecare nod 'u' avem inegalitatea d(u)<f(u). Nodul u este colorat in alb inainte de momentul d(u), este colorat in gri intre momentele de timp d(u) si f(u) si colorat in negru dupa momentul de timp f(u).
Se va prezenta pseudocodul algoritmului de cautare in adancime descris mai sus. Se considera drept intrare graful G, care poate fi orientat sau neorientat, si algoritmul foloseste o variabila globala time care este utilizata pentru marcarea stampilelor de timp.


Procedura de parcurgere in adancime, DFS, lucreaza dupa cum urmeaza:- primele linii coloreaza nodurile in alb si initializeaza campul parinte pentru fiecare nod al grafului, cu NIL si reseteaza contorul global de timp. Bucla for verifica fiecare nod din multimea V si atunci cand un nod alb este gasit el va fi vizitat aplicandu-se procedura DFS-VISIT. De fiecare data cand procedura DFS-VISIT este apelata, nodul "u" devine radacina a unui nou arbore din padurea in adancime. Cand ne intoarcem in procedura DFS, fiecarui nod u i-a fost asignat un timp de descoperire, d(u), si un timp de terminare f(u) (adica cele doua stampile de timp).
Initial, la fiecare apel al procedurii DFS-VISIT(u) nodul 'u' este alb, deci el va fi colorat in gri in prima linie a acestei proceduri, dupa care se inregistreaza stampila de timp si se actualizeaza variabila globala Time. Bucla for examineaza fiecare nod 'v' care este adiacent nodului 'u' si viziteaza in mod recursiv nodul 'v' daca el e alb. Fiecare nod 'v' ce apartine lui ADJ(u) este considerat ca fiind explorat prin parcurgere in adancime, deoarece se ia in considerare muchia (u,v). Dupa ce fiecare muchie care pleaca din nodul 'v' a fost explorata se coloreaza in negru nodul 'u' si se stampileaza cu timpul de terminare-prelucrare, adica variabila f(u).
Programul urmator prezinta implementarea procedurii DFS de parcurgere a grafurilor.
#include <stdio.h>
#include <values.h>
#define BIG MAXINT
enum ;
int grafs10ts10t,/* matricea de adiacenta a grafului */
n;/* numarul de noduri din graf */
int Ds10t,COLORs10t,PIs10t,Fs10t,TIME;
void DFS_VISIT(int u)
COLORsut=BLACK;
Fsut=TIME;
TIME=TIME+1;
return;
void DFS(void)
TIME=0;
for(u=1;u<n;u++)
if(COLORsut==WHITE)
DFS_VISIT(u);
main()
#include <stdio.h>
#include <values.h>
#define BIG MAXINT
enum ;
typedef struct yy stack,*pstack;
int grafs10ts10t,n;
int Ds10t,COLORs10t,PIs10t,Fs10t,TIME;
void DFS_VISIT(int u)
COLORsut=BLACK;
Fsut=TIME;
TIME=TIME+1;
return;
void DFS(void)
TIME=0;
for(u=1;u<n;u++)
if(COLORsut==WHITE)
DFS_VISIT(u);
main()
Exemplu
Urmatoarea figura reprezinta un exemplu aparut atunci cand cineva se imbraca, dimineata. Astfel, trebuie sa se imbrace cu anumite articole inaintea altora, de exemplu, sosetele inaintea pantofilor. Langa noduri au fost trecute si stampilele de timp obtinute in urma parcurgerii grafului cu algoritmul DFS.
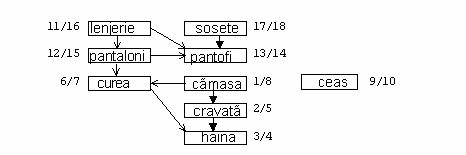
Muchia (u,v) din acest graf orientat aciclic indica faptul ca articolul 'u' trebuie sa fie imbracat inaintea articolului 'v'. Figura urmatoare arata sortarea topologica a acestui graf orientat aciclic ordonand nodurile pe o linie orizontala, astfel incat toate muchiile orientate sa mearga de la stanga la dreapta si pentru aceasta ordonarea este facuta descrescator dupa momentul de timp de incheiere a prelucrarii nodului.

Rezulta urmatorul algoritm de sortare topologica a unui graf orientat aciclic:

Rezulta ca se poate executa o sortare topologica intr-un timp O(|E|+|V|) deoarece acesta este timpul consumat de algoritmul DFS, iar pentru introducerea oricarui nod din multimea V in capul unei liste se consuma un timp O(1). Se pune problema demonstrarii corectitudinii algoritmului prezentat.
Lema 1
Un graf orientat, G, este aciclic daca si numai daca algoritmul de parcurgere in adancime nu furnizeaza muchii inapoi.
Demonstratie
'=>' Se presupune ca exista o muchie inapoi (u,v). Atunci nodul 'v' este un stramos al nodului 'u' in padurea in adancime, deci exista un drum de la nodul 'v' la nodul 'u' si muchia inapoi completeaza un ciclu.
'<=' Se presupune ca G contine ciclul 'c'. Se va arata ca algoritmul DFS furnizeaza o muchie inapoi. Fie primul nod care este descoperit in ciclul 'c', notat cu 'v', si fie muchia (u,v) o muchie care precede ciclul. La momentul de timp d(v) exista un drum de noduri albe de la nodul 'v' la nodul 'u'. Rezulta ca nodul 'u' devine un descendent al nodului 'v' in padurea in adancime, deci muchia (u,v) este o muchie inapoi.
Teorema 1
Algoritmul SORTARE-TOPOLOGICA (G) produce sortarea topologica a unui graf orientat aciclic.
Demonstratie
Se presupune ca algoritmul DFS se executa asupra unui graf orientat aciclic, G=(V,E), pentru a se determina timpii de terminare a prelucrarii tuturor nodurilor din graf. Este suficient sa se arate ca pentru orice pereche de noduri distincte 'u' si 'v' din V exista o muchie in G de la nodul 'u' la nodul 'v' daca f(v)<f(u).
Se considera o muchie (u,v) explorata de algoritmul DFS. Cand aceasta muchie este explorata, nodul 'v' nu poate fi gri deoarece atunci el ar putea fi un stramos al nodului 'u' si deci muchia (u,v) ar fi o muchie inapoi, ceea ce contrazice Lema 1. Deci nodul 'v' trebuie sa fie ori nod alb, ori nod negru. Daca nodul 'v' este alb el devine un descendent al nodului 'u' si astfel f(v)<f(u). Daca nodul 'v' este negru atunci f(v)<f(u). Deci pentru orice muchie (u,v) din graful orientat aciclic avem f(v)<f(u) ceea ce demonstreaza teorema.
Un algoritm simplu de gasire a unei ordonari topologice este urmatorul:
- cand se gaseste un nod oarecare care nu are muchii care intra in el, se tipareste aceasta valoare si se poate sterge impreuna cu muchiile lui din graf. Se poate aplica aceeasi strategie pentru restul grafului.
Pentru a formaliza aceasta idee se defineste i-gradul unui nod 'v' ca numarul de muchii (u,v). Se calculeaza i-gradul tuturor nodurilor din graf. Se presupune ca avem un masiv care este initializat cu i-gradul nodurilor grafului, iar graful este citit in liste de adiacenta dupa cum se arata mai jos (capetele listelor care reprezinta nodurile din graf se afla intr-un masiv).
Exemplu
Se considera urmatorul graf:
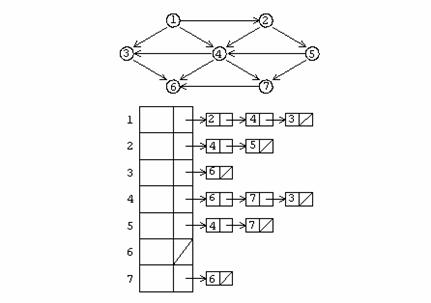
Deci pentru fiecare nod se pastreaza o lista a tuturor nodurilor adiacente lui. Daca spatiul cerut pentru o astfel de reprezentare este de ordinul O(|V|+|E|) avem un masiv cu noduri cap pentru lista de adiacenta a fiecarui nod.
Avand in vedere aceasta consideratie se poate da urmatoarea descriere a algoritmului de sortare topologica.

Functia GASESTE-NOD-NOU-DE-GRAD-ZERO, baleiaza masivul cu i-grade pentru cautarea unui nod care are i-gradul zero si caruia nu i-a fost asignat un numar topologic.
Procedura returneaza zero daca nici un astfel de nod nu exista si aceasta indica faptul ca graful dat contine un ciclu. Deoarece aceasta procedura realizeaza o parcurgere secventiala a masivului cu i-grade, fiecare apel al ei consuma un timp O(|V|). Deoarece sunt |V| astfel de apeluri timpul de rulare pentru algoritm este O(|V|2). Daca se proiecteaza cu atentie structura de date este posibil sa se imbunatateasca performantele algoritmului (deoarece motivul timpului de rulare mare este dat de parcurgerea secventiala a masivului).
Cand se cauta un nod de grad zero, se cerceteaza toate nodurile care sunt potential cu i-grad zero, chiar daca numai putine dintre ele si-au schimbat i-gradul. Se poate elimina aceasta ineficienta prin pastrarea tuturor nodurilor cu i-grad zero intr-o cutie speciala.
Functia GASESTE-NOD-NOU-DE-GRAD-ZERO returneaza si sterge orice nod din 'cutie'. Cand se decrementeaza i-gradul unui nod din lista de adiacenta se verifica fiecare nod si se plaseaza in cutie daca i-gradul lui a ajuns la zero. Pentru implementarea cutiei se poate folosi fie o stiva, fie o coada. La inceput i-gradul este calculat pentru fiecare nod, apoi toate nodurile cu i-grad zero sunt plasate intr-o coada care este initial vida. Atata timp cat coada nu este vida un nod 'v' este indepartat si toate muchiile adiacente nodului 'v' isi decrementeaza i-gradul lor. Un nod este pus in coada atunci cand i-gradul lui coboara la zero si rezulta ca ordinea topologica a nodurilor grafului este ordinea in care nodurile vor fi scoase din coada. Urmatoarea procedura prezinta o implementare in pseudocod a algoritmului imbunatatit:

Ca si inainte s-a presupus ca graful este citit si introdus intr-o lista de adiacenta, si s-a calculat i-gradul pentru fiecare nod si s-a plasat in masivul corespunzator. Un mod simplu de a face acest lucru in practica este de a plasa i-gradul fiecarui nod in campul unei liste. De asemenea se presupune ca masivul TOP-NUM in care sunt plasate numele din ordonarea topologica este o variabila globala. Timpul de executie pentru acest algoritm in cazul utilizarii reprezentarii grafului cu liste de adiacenta este (O(|E|+|V|)). Acest lucru rezulta din faptul ca ciclul for este executat cel putin o data pentru fiecare muchie, iar operatiile asupra cozii sunt executate cel mult o data pentru fiecare nod. Pasii de initializare consuma timp proportional cu dimensiunea grafului.
In continuare se prezinta implementarea in limbajul C a algoritmilor din acest paragraf:
Primul program implementeaza operatia de sortare topologica folosind primul algoritm prezentat.
#include <stdio.h>
/* graful este reprezentat prin liste de adiacenta si structurile urmatoare implementeaza aceasta reprezentare*/
typedef struct yy nADJ,*refADJ;
struct grafs10t;
int n;
int TOP_NUMs10t,VISITs10t;
void citeste()
for(i=0;i<n;i++)
}
grafsit.ADJ=head;
}
int FIND_NEW_VERTEX_OF_INDEGREE_ZERO()
void TOPOLOGICAL_SORT()
VISITsvt=1;
}
}
main()
Urmatorul program implementeaza al doilea algoritm de sortare topologica prezentat in acest paragraf.
#include <stdio.h>
/* structura urmatoare implementeaza o coada care
va fi folosita in algoritm */
typedef struct xx queue,*pqueue;
/* graful este reprezentat prin intermediul listelor de adicenta iar urmatoarele structuri implemeteaza acest lucru */
typedef struct yy nADJ,*refADJ;
struct grafs10t;
int n;
int TOP_NUMs10t,VISITs10t;
void citeste()
for(i=0;i<n;i++)
}
grafsit.ADJ=head;
}
void ENQ(pqueue *head,pqueue *tail,int nod)
return;
int DEQ(pqueue *head)
void TOPOLOGICAL_SORT()
}
if(count<n)
printf('GRAPH HAS A CYCLEin');
return;
main()
Probleme propuse
1. O statie de epurare a apei are N bazine de decantare unite prin conducte. Fiecare pereche de bazine poate fi unita sau nu printr-o conducta. Apa care trebuie purificata porneste dintr-un bazin initial S si trebuie sa ajunga la bazinul de iesire F.
Se cere determinarea numarului minim de bazine prin care trece apa pentru a fi purificata (breadth first search) si ordinea acestor bazine (sortare topologica).
2. Un student trebuie sa asambleze un dispozitiv folosind pentru aceasta o serie de componente. Pentru usurarea muncii, el isi aranjeaza componentele sub forma unei diagrame formata din noduri si arce. Nodurile corespund componentelor. Exista un arc de la o componenta C1 la o componenta C2 daca si numai daca componenta C2 poate fi asamblata la dispozitiv numai in urma asamblarii componentei C1. Diagrama este construita astfel incit sa nu existe dependente ciclice in ordinea de asamblare a componentelor.
Se cere alcatuirea unui plan de asamblare a dispozitivului astfel incit studentul sa aleaga corect la fiecare pas componenta necesara (sortare topologica).
Un soldat trebuie sa se echipeze pentru o actiune de lupta. Toate partile de echipament se afla in preajma sa si el stie toate perechile formate din cite doua parti de echipament pentru care nu se poate echipa cu o parte inaintea celeilalte.
Se cere alcatuirea unui plan de echipare astfel incit soldatul sa aleaga corect la fiecare pas, partea de echipament necesara (sortare topologica si graf dat prin lista de muchii).
4. Distribuirea cartilor la cititorii unei biblioteci este facuta de catre un robot care are posibilitatea sa ajunga la orice carte care poate fi ceruta. Din pacate, rafturile cu carti sunt dispuse astfel incit robotul nu poate lua cartile intr-un singur drum. Dupa primirea comenzilor de la mai multi cititori, robotul cunoaste pozitia cartilor in rafturi si drumurile catre carti. Robotul porneste si culege cartile care sunt accesibile intr-un drum, apoi porneste de la o alta pozitie de carte si culege acele carti care sunt accesibile din acel punct si asa mai departe (depth first search si arborii in adincime).
Sa se ordoneze apoi pozitiile cartilor (sortare topologica).
5 Componente tari - conexe si arbori de acoperire minima
Se va considera o aplicatie clasica pentru algoritmul de parcurgere in adancime a unui graf si anume descompunerea unui graf orientat in componentele lui tari-conexe.
Se va prezenta algoritmul de descompunere al grafului care foloseste doi algoritmi de parcurgere in adancime a grafului. Problema descompunerii grafului in componente tari-conexe are o corespondenta in problemele practice. Astfel problema originala poate fi impartita in mai multe subprobleme, fiecare din ele corespunzad unei componente tari-conexe. Se rezolva subproblemele si prin combinarea solutiilor rezulta structura care poate fi reprezentata ca solutie a problemei date. De fapt este o conexiune intre componentele tari-conexe si aceasta structura poate fi reprezentata de un graf.
Definitie
O componenta tare-conexa a unui graf
orientat G=(V, E) este multimea maxima de noduri U ![]() V
astfel incat pentru orice pereche de noduri (u, v) avem relatiile: u~ v si v~ u care semnifica
faptul ca nodurile u si v pot fi atinse unul din altul.
V
astfel incat pentru orice pereche de noduri (u, v) avem relatiile: u~ v si v~ u care semnifica
faptul ca nodurile u si v pot fi atinse unul din altul.
Exemplu
Se va considera un graf orientat G in care fiecare nod este etichetat cu timpii de descoperire si terminare a prelucrarii.
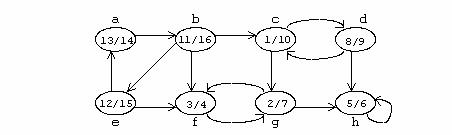
Componentele tari-conexe pentru G sunt: ; ; ; .
Algoritmul care gaseste componentele tari-conexe pentru un graf G dat va utiliza graful transpus.
Astfel fie G=(V, E) graful dat, atunci graful transpus este: GT=(V, ET) unde ET=. Deci multimea ET este data de muchiile din E la care s-a inversat sensul.
Dandu-se o reprezentare cu lista de adiacenta pentru un graf G, atunci timpul de creare a grafului GT este desigur O(|E|+|V|). Se observa ca grafurile G si GT au exact aceleasi componente tari-conexe deoarece u si v sunt noduri care se ating pornind din unul sau din celalalt in G daca si numai daca ele pot fi atinse unul din altul in graful GT.
Exemplu
Figura urmatoare arata graful transpus pentru graful din exemplul anterior .
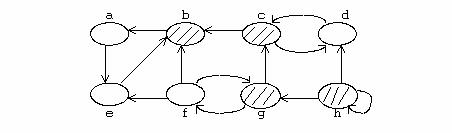
Fiecare componenta tare-conexa corespunde la un arbore in adancime. Nodurile b, c, g si h (hasurate) sunt stramosii fiecarui nod din componenta tare-conexa corespunzatoare. Aceste noduri sunt de asemenea radacinile arborelui in adancime, care sunt produsi de parcurgerea in adancime a grafului dat (in cazul figurii de mai sus, graful GT).
Se prezinta un algoritm liniar in timp care determina componentele tari-conexe pentru un graf orientat dat utilizand doi algoritmi de cautare in adancime - unul pentru graful G dat, celalalt pentru graful transpus corespunzator GT.

Lema
Daca doua noduri sunt in aceeasi componenta tare-conexa, atunci nici un drum intre ele nu paraseste aceea componenta tare-conexa.
Demonstratie
Fie doua noduri oarecare u si v in aceeasi componenta tare-conexa. Prin definitia componentei tare-conexa, exista un drum de la nodul u la nodul v si exista un drum de la nodul v la nodul u. Fie w un nod care se afla pe drumul de la nodul u la nodul v si deci se poate scrie: u~ w~ v, adica nodul w poate fi atins din nodul u. Deoarece avem nodul u care poate fi atins din nodul v adica v~ u rezulta ca nodul u poate fi atins din nodul w scriind w~ v~ u. Deci nodurile u si w se afla in aceeasi componenta tare-conexa. Deoarece nodul w a fost ales arbitrar rezulta ca lema este adevarata.
In continuare notatiile d(u) si f(u) se vor referi la timpul de descoperire si timpul de terminare a prelucrarii, calculati cu algoritmul DFS din prima linie a procedurii COMPONENTA-TARE-CONEXA de mai sus. In mod similar notatia u~ v se refera la existenta unui drum in graful G (si nu in graful transpus GT).
Pentru a demonstra corectitudinea algoritmului COMPONENTA- TARE-CONEXA, se introduce notatia: FI(u) care reprezinta stramosul nodului u si care este un nod w care poate fi atins din nodul u si care are ultimul timp de terminare a prelucrarii dat de algoritmul DFS din prima linie a procedurii de mai sus. Cu alte cuvinte FI(u) este egal cu acel nod w astfel incat u~ w si f(w) are valoare maxima.
Se noteaza faptul ca
FI(u)=u este o relatie posibila deoarece u poate fi atins din el insusi
si deci vom avea f(u)![]() (FI(u)) (1).
(FI(u)) (1).
De asemenea, se remarca faptul ca
FI(FI(u))=FI(u). Din urmatoarele motive pentru orice noduri u, v![]() V,
u~ v implica
faptul: f(FI(v))
V,
u~ v implica
faptul: f(FI(v))![]() (FI(u)) (2).
(FI(u)) (2).
Deoarece avem: ![]() si stramosul
are timpul maxim de terminare a prelucrarii pentru toate nodurile care pot fi
atinse. Deoarece FI(u) este atins din nodul u formula (2) implica faptul ca
avem: f(FI(FI(u)))
si stramosul
are timpul maxim de terminare a prelucrarii pentru toate nodurile care pot fi
atinse. Deoarece FI(u) este atins din nodul u formula (2) implica faptul ca
avem: f(FI(FI(u)))![]() (FI(u)).
(FI(u)).
Din relatia (1) avem: f(FI(u)) ![]() (FI(FI(u))) si rezulta deci ca f(FI(FI(u)) =
f(FI(u)) si astfel se obtine: FI(FI(u))=FI(u), deoarece doua noduri care au
acelasi timp de terminare al prelucrarii sunt de fapt acelasi nod.
(FI(FI(u))) si rezulta deci ca f(FI(FI(u)) =
f(FI(u)) si astfel se obtine: FI(FI(u))=FI(u), deoarece doua noduri care au
acelasi timp de terminare al prelucrarii sunt de fapt acelasi nod.
Se va arata ca fiecare componenta tare-conexa are un nod care este stramosul oricarui alt nod din componenta tare-conexa. Acest stramos este nodul reprezentativ pentru componenta tare-conexa. Avand in vedere algoritmul de parcurgere in adancime al grafului G, acest nod este primul nod al componentei tari-conexe, care este descoperit si este ultimul nod al componentei asupra caruia se actioneaza. In algoritmul de parcurgere in adancime a grafului GT acesta este radacina arborelui in adancime.
Urmatoarul rezultat justifica denumirea de stramos al nodului u data nodului FI(u).
Propozitie
Intr-un graf orientat G=(V, E) stramosul FI(u) al oricarui nod uIV este determinat de algoritmul de parcurgere in adancime aplicat grafului G.
Demonstratie
Daca FI(u)=u atunci teorema este evidenta.
Daca FI(u)¹u se considera culorile nodurilor la momentul de timp d(u).
Daca FI(u) este innegrit atunci f(FI(u))<f(u) ceea ce contrazice inegalitatea (1).
Daca FI(u) este gri atunci el este un stramos al nodului u si teorema este demonstrata.
Ramane deci sa se arate ca FI(u) nu are culoarea alba.
Exista doua cazuri cu privire la culorile nodurilor intermediare care se gasesc pe drumul dintre nodul u si nodul FI(u):
1) daca fiecare nod intermediar este alb atunci FI(u) devine un descendent a lui u si conform teoremei drumului alb [vezi 9 si 10] avem: f(FI(u))<f(u) ceea ce contrazice inegalitatea (1).
2) daca avem un nod oarecare, intermediar, de culoare diferita de alb;- fie t ultimul nod cu culoarea diferita de alb de pe drumul de la nodul u la nodul FI(u). Atunci, nodul t trebuie sa fie gri deoarece nu exista o muchie de la un nod negru, la un nod alb si succesorul nodului t este alb. Acest lucru arata ca exista un drum de noduri albe de la nodul t la nodul FI(u) si astfel nodul FI(u) este un descendent al nodului t conform teoremei drumului alb. Acest lucru implica: f(t)>f(FI(u)) ceea ce contrazice alegerea nodului FI(u) deoarece exista un drum de la nodul u la nodul t.
Corolar
Pentru orice algoritm de parcurgere
in adancime aplicat unui graf orientat, nodurile u si FI(u) se afla in
aceeasi componenta tare-conexa, oricare ar fi nodul u![]() V.
V.
Demonstratie
Avem: u~ FI(u) din definita stramosului si vom avea si FI(u)~ u, deoarece FI(u) este stramosul lui u.
Urmatoarea teorema prezinta un rezultat mai puternic relativ la stramosii din componenta tare-conexa.
Teorema
Se considera un graf orientat G=(V,
E) si doua noduri u, v![]() V.
Atunci nodurile u si v se afla in aceeasi componenta tare-conexa daca si numai
daca ele au acelasi stramos dat de algoritmul de parcurgere in adancime
aplicat grafului G.
V.
Atunci nodurile u si v se afla in aceeasi componenta tare-conexa daca si numai
daca ele au acelasi stramos dat de algoritmul de parcurgere in adancime
aplicat grafului G.
Demonstratie
'=>' se presupune ca nodurile u si v sunt in aceeasi componenta tare-conexa. Orice nod care poate fi atins din nodul u poate fi atins din nodul v si viceversa, deoarece exista drumuri in ambele directii, intre nodurile u si v. Din definitia stramosului se trage concluzia ca FI(u)=FI(v).
'<=' se presupune ca FI(u)=FI(v). Din corolarul dat, nodul u este in aceeasi componenta tare-conexa cu nodul FI(u), iar nodul v este in aceeasi componenta tare-conexa cu nodul FI(v), deci nodurile u si v se afla in aceeasi componenta tare-conexa.
Avand in vedere propozitia data, structura algoritmului componentei tari-conexe poate fi inteleasa mai usor. Componentele tari-conexe sunt multimi de noduri care au acelasi stramos. Mai mult, din propozitia data si teorema parantezelor [vezi 9 si 10] rezulta ca aplicarea algoritmului DFS din prima linie a procedurii anterioare da un stramos care are primul timp de descoperire si ultimul timp de terminare a prelucrarii in propria componenta tare-conexa.
Pentru a intelege de ce se aplica algoritmul DFS asupra grafului transpus GT se considera un nod r care are cel mai mare timp de terminare a prelucrarii, calculat cu algoritmul DFS din prima linie (deci aplicat grafului G).
Din definitia stramosului, nodul r trebuie sa fie un astfel de stramos si el este propriul lui stramos deoarece poate fi atins din el insusi si nici un alt nod din graf nu are un timp de terminare a prelucrarii mai mare.
Se pune problema care sunt celelalte noduri din componenta tare-conexa corespunzatoare nodului r. Aceste noduri sunt cele care au drept stramos nodul r, adica care pot fi atinse din nodul r, dar care nu pot atinge orice alt nod cu un timp de terminare a prelucrarii mai mare de f(r).
Dar timpul de terminare a prelucrarii nodului r este maxim pentru orice nod ce apartine lui G. Deci nodurile din componenta tare-conexa corespunzatoare nodului r sunt acele noduri care pot atinge nodul r. Echivalent, componenta tare-conexa a nodului r consta din acele noduri care pot atinge nodul r in graful transpus GT, astfel, algoritmul DFS din a treia linie identifica toate nodurile din componenta tare-conexa a nodului r si le innegreste. Dupa ce algoritmul DFS din a treia linie a procedurii identifica nodurile componentei tare-conexe a nodului r, considera un alt nod p care are cel mai mare timp de terminare a prelucrarii din nodurile ramase. Nodul p trebuie sa fie propriul sau stramos deoarece nu poate fi atins dintr-un alt nod care sa aiba timpul de terminare a prelucrarii mai mare (altfel ar fi inclus in componenta tare-conexa a nodului r).
Din ratiuni similare orice nod care poate atinge nodul p si care nu e colorat deja in negru trebuie sa apartina componentei tari-conexe a nodului p. Astfel algoritmul DFS din cea de-a treia linie continua cu identificarea si colorarea in negru a fiecarui nod din componenta tare-conexa a nodului r prin cautarea pornind de la nodul p in graful GT. Deci algoritmul DFS din a treia linie determina una cate una fiecare componenta tare-conexa. Fiecare astfel de componenta este identificata in algoritmul DFS prin apelarea algoritmului DFS-VISIT aplicat stramosului componentei respective.
Apelurile recursive ale algoritmului DFS-VISIT coloreaza in negru fiecare nod al componentei respective. Cand revenim din algoritmul DFS-VISIT in algoritmul DFS, intreaga componenta tare-conexa are noduri de culoarea neagra si a fost determinata. Algoritmul DFS considerand nodurile ramase (diferite de culoarea neagra), alege nodul cu timpul de terminare a prelucrarii maxim si acest nod devine un stramos pentru o alta componenta tare-conexa si procesul continua.
Se poate acum enunta:
Teorema
Algoritmul COMPONENTA-TARE-CONEXA (G) calculeaza corect componentele tari-conexe ale unui graf orientat G.
Demonstratie
Se va demonstra prin inductie considerand numarul de arbori in adancime gasiti de algoritmul de parcurgere in adancime aplicat grafului GT. Fiecare pas al procesului de inductie arata ca arborele format la aplicarea algoritmului DFS grafului GT este o componenta tare-conexa (presupunand ca toti arborii anteriori produsi sunt componente tari-conexe). Cazul de baza este evident pentru ca primul arbore produs nu are nici un alt arbore produs anterior si deci presupunerea este adevarata.
Se considera un arbore in adancime T care are radacina r si care este obtinut prin aplicarea algoritmului DFS asupra grafului GT. Fie C(r) multimea nodurilor care au drept stramos nodul r adica: C(r)=.
Se va demonstra ca
un nod u este plasat in arborele T daca si numai daca u![]() C(r).
C(r).
'<=' Propozitia data
implica faptul ca orice nod care apartine lui C(r) se afla in acelasi arbore in
adancime. Deoarece nodul r![]() C(r)
este radacina pentru arborele T, orice nod care este in multimea C(r) se afla
in arborele T.
C(r)
este radacina pentru arborele T, orice nod care este in multimea C(r) se afla
in arborele T.
'=>' Se va arata ca
pentru un nod oarecare w avem:
f(FI(w))>f(r) sau f(FI(w))<f(r) si pentru acest nod nu putem sa scriem w![]() T.
T.
Prin inductia asupra numarului de
arbori gasiti, orice nod w, astfel incat f(FI(w))>f(r), nu este
plasat in arborele T deoarece la momentul de timp cand este selectat w, nodul r a fost deja plasat in arborele
cu radacina FI(w). Orice nod w pentru care avem cea de-a doua
inegalitate: f(FI(w))<f(r) nu poate fi plasat in arborele T deoarece o
astfel de plasare ar implica faptul: w~ r si din formula (2) cu proprietatea ca r=FI(r) se
obtine f(FI(w))![]() (FI(r))=f(r)
care contrazice presupunerea f(FI(w))<f(r). Deci arborele T contine numai
acele noduri u pentru care se poate scrie FI(u)=r, adica T este exact
componenta tare-conexa C(r), lucru care completeaza demonstratia inductiva.
(FI(r))=f(r)
care contrazice presupunerea f(FI(w))<f(r). Deci arborele T contine numai
acele noduri u pentru care se poate scrie FI(u)=r, adica T este exact
componenta tare-conexa C(r), lucru care completeaza demonstratia inductiva.
In continuare se prezinta implementarea algoritmului care calculeaza componentele tari conexe dintr-un graf orientat:
#include <stdio.h>
#include <alloc.h>
#define TRUE 1
#define FALSE 0
#define MAXNOD 20
/* implementarea grafului este realizata folosind listele de adiacenta si urmatoarele structuri implementeaza acest lucru */
typedef struct s *prefnod, refnod;
typedef struct x graf_type[MAXNOD];
int nr_nod;
graf_type G;
void DFS(graf_type G,
int nr_nod,
int v,
int VISITED[],
int TIME[],
int *tc)
return;
void DFS1(graf_type G,
int nr_nod,
int v,
int VISITED[],
int TIME[],
int *tc)
return;
void citeste_graf(graf_type G, int *nr_nod)
}
fclose(fin);
return;
void tipareste_graf(graf_type G, int nr_nod)
return;
void STRONGLY_CONNECTED_COMPONENTS(graf_type G, int nr_nod)
printf('Graful initial:n');
tipareste_graf(G, nr_nod);
for(i=0; i<nr_nod; i++)
if(VISITED[i]==FALSE)
DFS1( G, nr_nod, i, VISITED, TIME, &tp);
/* se ordoneaza dupa timpii de vizitare */
for(i=0; i<nr_nod-1; i++)
if(poz_max != i)
}
for(i=0; i<nr_nod; i++)
/* se calculeaza graful transpus */
for(i=0;i<nr_nod;i++)
}
for(i=0; i<nr_nod; i++)
VISITED[i]=FALSE;
tp=0;
printf('Graful transpus:n');
tipareste_graf(GT, nr_nod);
printf('Componenete tare conexe:n');
for(i=0;i<nr_nod;i++)
if(VISITED[REFNOD[i]]==FALSE)
return;
int main()
Observatie
In procesul de proiectare a circuitelor electronice este adesea necesar sa se faca legatura dintre pinii mai multor componente electronice echivalente. Interconectarea unor multimi cu n-pini poate fi facuta prin diferite aranjamente a (n-1) fire de legatura a doi pini. Dintre toate aranjamentele posibile, cea care intereseaza este cea care are cea mai mica cantitate de fire.
Se poate modela aceasta problema a conectarii
pinilor, cu ajutorul unui graf neorientat G=(V, E) unde V - multimea pinilor
iar E - multimea interconectarilor posibile dintre perechi de pini. Pentru
fiecare muchie (u, v) apartinand lui E se considera o pondere W(u, v)
specificand costul conectarii nodului u cu nodul v (cantitatea de
fire necesara). Se doreste sa se gaseasca o submultime aciclica T![]() E
care conecteaza toate nodurile posibile si a carei pondere totala W(T)=W(u, v)
sa fie minima. Deoarece T este o multime aciclica de muchii si conecteaza toate
nodurile, ea trebuie sa formeze un arbore care se va numi arborele de
acoperire deoarece el masoara graful G.
E
care conecteaza toate nodurile posibile si a carei pondere totala W(T)=W(u, v)
sa fie minima. Deoarece T este o multime aciclica de muchii si conecteaza toate
nodurile, ea trebuie sa formeze un arbore care se va numi arborele de
acoperire deoarece el masoara graful G.
Problema determinarii arborelui T se numeste problema arborilor de acoperire minima.
Observatie
Fraza arbori de acoperire minima este o formula prescurtata a frazei arbore de acoperire cu pondere minima. De fapt nu se minimizeaza numarul de muchii din arborele T deoarece toti arborii de acoperire au exact (|v|-1) muchii.
Exemplu
Se prezinta un graf conex si arborele lui de acoperire minima [10].
Sunt aratate ponderile muchiilor iar muchiile din arborele de acoperire sunt dublate.
Ponderea totala a arborelui este 37. Se poate demonstra ca arborele de acoperire nu este unic.
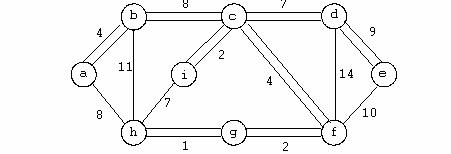
Astfel daca se elimina muchia (b, c) cu ponderea 8 si se inlocuieste cu muchia (a, h) care are tot ponderea 8 rezulta un alt arbore de acoperire minim cu ponderea 37.
In acest paragraf se va prezenta un algoritm generic pentru obtinerea arborelui de acoperire minima prin gasirea arborelui prin adaugari succesive de muchii la fiecare moment de timp. In paragraful urmator se vor prezenta doi algoritmi care implementeaza algoritmul generic.
Se presupune ca avem un graf
neorientat, conex G=(V, E) si avem o functie de ponderare w:E![]() R
si se doreste sa se gaseasca arborele de acoperire minima a grafului G.
Algoritmul care va fi prezentat utilizeaza metoda GREEDY de rezolvare a
problemelor. Strategia GREEDY folosita de algoritmul generic, obtine arborele
de acoperire minima adaugand cate o muchie convenabila la un arbore de
acoperire minima dat, la un moment dat. Algoritmul
utilizeaza o multime A de muchii care este intotdeauna o submultime a arborelui
de acoperire minima. La fiecare pas se determina o muchie (u, v) care poate fi
adaugata la multimea A fara sa se violeze conditia invarianta in sensul ca
multimea A
R
si se doreste sa se gaseasca arborele de acoperire minima a grafului G.
Algoritmul care va fi prezentat utilizeaza metoda GREEDY de rezolvare a
problemelor. Strategia GREEDY folosita de algoritmul generic, obtine arborele
de acoperire minima adaugand cate o muchie convenabila la un arbore de
acoperire minima dat, la un moment dat. Algoritmul
utilizeaza o multime A de muchii care este intotdeauna o submultime a arborelui
de acoperire minima. La fiecare pas se determina o muchie (u, v) care poate fi
adaugata la multimea A fara sa se violeze conditia invarianta in sensul ca
multimea A![]() este de asemenea o submultime a arborelui de acoperire minima. Muchia (u,
v) care poate fi adaugata astfel la multimea A, se numeste muchie sigura
pentru A, deoarece ea nu distruge conditia invarianta.
este de asemenea o submultime a arborelui de acoperire minima. Muchia (u,
v) care poate fi adaugata astfel la multimea A, se numeste muchie sigura
pentru A, deoarece ea nu distruge conditia invarianta.
Algoritmul este:

Dupa prima linie, A este vida si
satisface invariantul, adica este o submultime a arborelui de acoperire minima,
iar bucla WHILE pastreaza acest invariant. Cand se iese din procedura
GENERIC-ARB-ACOP-MIN, multimea A trebuie sa fie un arbore de acoperire minima.
Partea interesanta a algoritmului este desigur cea in care se gaseste muchia
sigura pentru multimea A. O astfel de muchie trebuie sa existe deoarece, cand
aceasta procedura este executata, invariantul cere sa existe un arbore de
acoperire T astfel incat A![]() T
si daca exista o muchie (u, v) apartinand lui T astfel incat muchia (u, v)
T
si daca exista o muchie (u, v) apartinand lui T astfel incat muchia (u, v)![]() A
atunci muchia (u, v) este o muchie sigura pentru multimea A.
A
atunci muchia (u, v) este o muchie sigura pentru multimea A.
Se va prezenta o regula de recunoastere a muchiilor sigure iar in paragraful urmator se descriu doi algoritmi, al lui KRUSKAL si al lui PRIM, care utilizeaza aceasta regula pentru gasirea eficienta a muchiilor sigure.
Pentru aceasta se vor introduce cateva notiuni:
Se numeste taietura perechea (S, VS) pentru un graf neorientat G=(V, E) o portiune a lui V. Se spune ca o muchie (u, v) apartinand lui E, traverseaza taietura (S, V-S) daca muchia are un nod in S si celalalt nod in VS. Se spune ca o taietura respecta multimea de muchii, daca nici o muchie din A nu traverseaza taietura.
O muchie se spune ca este o muchie usoara daca traverseaza o taietura si ponderea ei este minima pentru toate muchiile care traverseaza taietura. Se noteaza faptul ca pot exista mai multe muchii usoare care traverseaza o taietura in cazul in care acestea sunt legate. In general se spune ca o muchie este usoara daca ea satisface o proprietate data, adica daca ponderea ei este minima dintre toate muchiile care satisfac proprietatea data.
Exemplu
In figura urmatoare se arata doua moduri de privire a unei taieturi (S, V-S) pentru graful din exemplul anterior.
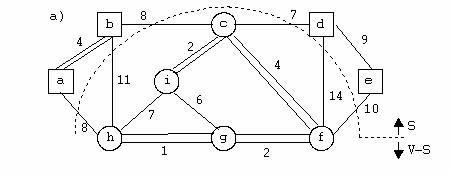
Nodurile din multimea S sunt reprezentate prin dreptunghiuri, muchiile care traverseaza taietura sunt cele care conecteaza nodurile albe (in figura reprezentate prin cerc) cu cele reprezentate prin dreptunghiuri. Muchia (b, c) este singura muchie usoara care traverseaza taietura. O submultime A de muchii este prezentata prin dubla muchie. Se noteaza faptul ca taietura VS respecta multimea A deoarece nici o muchie din A nu traverseaza taietura.
Acelasi graf este prezentat intr-o alta maniera astfel incat nodurile din S sunt la stanga iar cele din V-S se afla la dreapta. O muchie traverseaza taietura daca ea conecteaza un nod din stanga cu unul din dreapta.
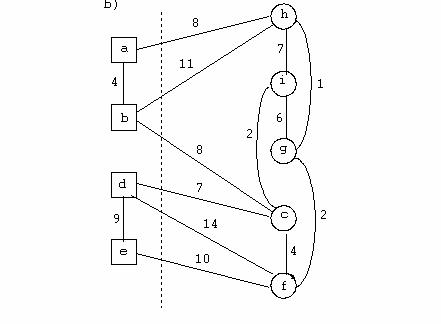
Urmatoarea teorema da un criteriu pentru recunoasterea unei muchii sigure.
Teorema
Fie G=(V, E) un graf neorientat
conex, cu ponderi reale atasate muchiilor si o functie de pondere W:E![]() R.
Fie A
R.
Fie A![]() E
care este inclusa intr-un arbore de acoperire minima a lui G. Fie (S, VS) o
taietura pentru G care respecta multimea A. Fie muchia (u, v) o muchie usoara
care traverseaza taietura (S, V-S). Atunci muchia (u, v) este sigura pentru A.
E
care este inclusa intr-un arbore de acoperire minima a lui G. Fie (S, VS) o
taietura pentru G care respecta multimea A. Fie muchia (u, v) o muchie usoara
care traverseaza taietura (S, V-S). Atunci muchia (u, v) este sigura pentru A.
Demonstratie
Fie T arborele de acoperire minima care include multimea A. Se presupune ca T nu contine muchia usoara (u, v) deoarece daca o contine demonstratia s-a terminat.
Se va construi un alt arbore de
acoperire minima notat T' care include multimea A![]() aratand ca muchia (u, v) este o muchie sigura pentru A. Muchia (u, v) formeaza
un ciclu cu muchiile unui drum p de la nodul u la nodul v in
arborele T dupa cum se ilustreza in figura urmatoare:
aratand ca muchia (u, v) este o muchie sigura pentru A. Muchia (u, v) formeaza
un ciclu cu muchiile unui drum p de la nodul u la nodul v in
arborele T dupa cum se ilustreza in figura urmatoare:
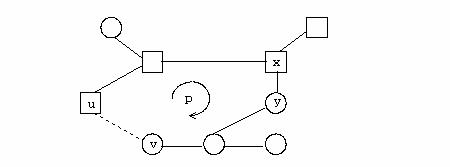
Deoarece nodurile u si v sunt de o parte si de alta a taieturii (S, VS), exista cel putin o muchie in T pe drumul p care de asemenea traverseaza taietura. Fie aceasta (x, y).
Muchia (x, y) nu este in A deoarece
taietura respecta multimea A. Deoarece (x, y) se afla pe drumul unic de la u
la v in arborele T, stergerea muchiei (x, y) rupe pe T in doua
componente. Adaugarea muchiei (u, v) conecteaza aceste doua componente formand
un arbore de acoperire T' astfel: T'=(T-)![]() . Se
arata acum faptul ca T' este un arbore de acoperire minima. Deoarece muchia (u,
v) este o muchie usoara care traverseaza taietura (S, VS) si muchia (x, y)
traverseaza de asemenea taietura, vom avea:
. Se
arata acum faptul ca T' este un arbore de acoperire minima. Deoarece muchia (u,
v) este o muchie usoara care traverseaza taietura (S, VS) si muchia (x, y)
traverseaza de asemenea taietura, vom avea:
W(u, v)![]() W(x, y) deci
W(T')=W(T)-W(x, y)+W(u, v)
W(x, y) deci
W(T')=W(T)-W(x, y)+W(u, v)![]() W(T).
W(T).
Dar T este un arbore de acoperire
minima, deci W(T) ![]() W(T') astfel
incat T' trebuie sa fie un arbore de acoperire minima de asemenea. Ramane sa
aratam ca muchia (u, v) este o muchie sigura pentru A. Avem desigur A
W(T') astfel
incat T' trebuie sa fie un arbore de acoperire minima de asemenea. Ramane sa
aratam ca muchia (u, v) este o muchie sigura pentru A. Avem desigur A![]() T', deoarece
A
T', deoarece
A![]() T. Muchia
(x, y)
T. Muchia
(x, y)![]() A => A
A => A![]() inclusa in T' si deoarece T' este un arbore de acoperire minima avem muchia (u,
v) muchie sigura pentru multimea A.
inclusa in T' si deoarece T' este un arbore de acoperire minima avem muchia (u,
v) muchie sigura pentru multimea A.
Teorema de mai sus poate fi aplicata pentru intelegerea modului de lucru a algoritmului GENERIC-ARB-ACOP-MIN. Dupa cum algoritmul lucreaza, multimea A este intotdeauna aciclica, altfel arborele de acoperire minima care include pe A ar contine un ciclu ceea ce este o contradictie.
In orice punct al executiei algoritmului, graful GA=(V, A) este o padure si fiecare din componentele conexe ale lui GA este un arbore (cand algoritmul incepe, arborii contin exact un nod, multimea A este vida si padurea contine exact |V| arbori cu un singur nod).
Orice muchie sigura (u, v) pentru A conecteaza componente distincte din graful GA deoarece AÈ trebuie sa fie aciclic.
Bucla din algoritmu GENERIC-ARB-ACOP-MIN este executata de un numar (|V|-1) ori pentru fiecare din cele (|V|-1) muchii ale unui arbore de acoperire minima care este determinat succesiv. Initial cand A este vida exista |V| arbori in GA si fiecare iteratie reduce acest numar cu o unitate. Cand padurea contine un singur arbore algoritmul se termina.
Corolar
Fie G=(V, E) un graf neorientat
conex cu functia de ponderare W:E![]() R
si fie A o submultime a lui E care este inclusa intr-un arbore de acoperire
minima a lui G si fie C o componenta conexa in padurea GA=(V,
A). Daca muchia (u, v) este o muchie usoara care conecteaza componenta C la o
alta componenta in GA, atunci muchia (u, v) este o muchie sigura
pentru A.
R
si fie A o submultime a lui E care este inclusa intr-un arbore de acoperire
minima a lui G si fie C o componenta conexa in padurea GA=(V,
A). Daca muchia (u, v) este o muchie usoara care conecteaza componenta C la o
alta componenta in GA, atunci muchia (u, v) este o muchie sigura
pentru A.
Demonstratie
Taietura (C, VC) respecta multimea A si deci muchia (u, v) este o muchie usoara pentru aceasta taietura.
Probleme propuse
1. In oraselul copiilor exista o retea de linii pe care se plimba carucioare care pot sa ia cite un copil. In nodurile retelei copiii pot primi cadouri. Fiecare copil are preferinte pentru anumite cadouri.
Se cere determinarea nodurilor din cadrul retelei, pentru care copiii trebuie sa se suie intr-un anumit carucior, astfel incit sa aiba sansa ca in drumul lor sa primeasca cel putin unul dintre cadourile dorite (componente conexe).
2. Pe o tarla agricola sunt mai multe parcele care trebuie cosite. Parcelele de diferite culturi (lucerna, trifoi, iarba, furaje) trebuie cosite de diferiti muncitori care lucreaza numai la un anumit fel de cultura (de exemplu numai la lucerna). Terenul agricol se modeleaza printr-o matrice M*N. Fiecare element al matricii corespunde unei multimi de un anumit tip. Doua elemente ale matricii sunt vecine daca au o muchie comuna. O parcela este o multime maximala de elemente astfel incit un muncitor se poate deplasa intre oricare doua elemente de-a lungul a doua elemente vecine.
Se cere numarul de muncitori care pot sa coseasca o cultura data (componente conexe).
Se considera o multime de N societati comerciale. Fiecare societate are datorii la alte societati si de asemenea are de primit bani de la alte societati. Pentru achitarea datoriilor fiecare societate poate plati toate sumele datorate, urmind sa primeasca la rindul sau sumele cuvenite de la societatile datornice. Procesul achitarii datoriilor se poate bloca daca exista societati comerciale care nu dispun de intreaga suma datorata celorlalte societati, chiar daca suma aflata in posesie ar acoperi diferenta dintre suma datorata si cea cuvenita. In cazul in care sumele disponibile sunt suficiente, urmeaza sa se stabileasca subgrupurile de societati comerciale care au datorii reciproce, datoriile urmind sa se reglementeze intre societatile din aceste subgrupuri.
Se cere determinarea subgrupurilor de societati care isi vor reglementa datoriile intre ele (componente tari conexe).
4. O companie telefonica isi stabileste o noua retea de cabluri telefonice. Se vor conecta mai multe zone care sunt numerotate cu intregi de la 1 la N si nu exista doua zone cu acelasi numar. Liniile telefonice sunt bidirectionale si intotdeauna conecteaza doua zone. In fiecare zona, linia se termina intr-un dispozitiv de legatura cu alta zona. Exista un singur dispozitiv de legatura cu alta zona, in fiecare din zonele date. Din fiecare zona este posibil sa se apeleze alte zone prin intermediul liniilor telefonice, totusi acest lucru nu se intimpla direct intotdeauna si se poate face legatura prin intermediul dispozitivelor de legatura din alte zone. Se poate intimpla ca la un moment dat un dispozitiv sa nu functioneze. Din acest motiv, pe linga faptul ca zona respectiva nu mai poate fi apelata, s-ar putea sa nu mai poata fi apelate nici alte zone care erau legate prin intermediul acesteia la retea. In acest caz se poate spune ca zona respectiva este o 'zona critica'.
Se cere sa se determine numarul de astfel de zone critice pentru o retea data. (componente biconexe si puncte de articulatie).
6 Algoritmii lui KRUSKAL si PRIM
Se vor prezenta doi algoritmi pentru determinarea arborelui de acoperire minima elaborati pe baza algoritmului generic prezentat anterior. Adica, fiecare din ei va avea o regula specifica pentru determinarea muchiei sigure prezentata in algoritmul GENERIC -ARB -ACOP -MIN.
In algoritmul KRUSKAL multimea A este o padure. Muchia sigura adaugata multimii A este intotdeauna o muchie de pondere minima din graful G conecteaza doua componente distincte. In algoritmul lui PRIM, muchiile din multimea A formeaza un singur arbore. De asemenea muchia sigura adaugata la multimea A este intotdeauna o muchie de pondere minima, dar ea conecteaza arborele la un nod care nu se afla in arbore.
Algoritmul lui KRUSKAL se bazeaza direct pe metoda de programare GREEDY deoarece, la fiecare pas el adauga o muchie la padure, astfel incat aceasta sa aiba ponderea cea mai mica posibila.
Implementarea care se va prezenta pentru acest algoritm se bazeaza pe multimi disjuncte de elemente, fiecare multime continand nodurile dintr-un arbore din padurea curenta. Rutina GASESTE-MULTIME (u) returneaza un element reprezentativ din multimea care contine nodul u, pentru a se putea determina daca doua noduri u si v apartin la acelasi arbore. Pentru aceasta se testeaza daca GASESTE-MULTIME T(u) este egal cu GASESTE-MULTIME (v). Desigur ca in pseudocodul care se prezinta, combinarea arborilor este realizata de rutina UNIUNE.

Rutina GASESTE-MULTIME (x) creaza o multime cu un singur membru indicat de 'x'. Deoarece multimile sunt disjuncte se cere ca 'x' sa nu faca parte deja din multime. La inceputul algoritmului se doreste multimea A si se creeaza un numar de |V| arbori care contin doar cate un nod. Muchiile din E sunt ordonate crescator dupa ponderea lor. Cel de al doilea ciclu FOR verifica pentru fiecare muchie (u, v) daca capetele muchiei (u, v) apartin la acelasi arbore. Daca nodurile se afla in acelasi arbore, atunci muchia (u, v) nu poate fi adaugata la padure fara sa se creeze un ciclu (pentru acest caz muchia este inlaturata).
Altfel cele doua noduri apartin la arbori diferiti si muchia (u, v) va fi adaugata la multimea A si nodurile celor doi arbori sunt amestecate. Timpul de lucru al algoritmului KRUSKAL pentru un graf G=(V, E) depinde de implementarea structurii pentru multimile disjuncte. Desigur timpul pentru initializari este O(|V|), iar timpul de sortare a muchiilor dupa ponderea lor este O(|E| log|E|). Exista O(|E|) operatii asupra multimilor disjuncte, deci in total se va consuma un timp O(|E|.A(E, V)) unde functia A(E, V) este functia lui ACKERMANN si calculul ei este de ordinul lui O(log|E|). In cazul nostru rezulta ca timpul total de executie al acestui algoritm este O(|E| log|E|).
Exemplu
Se va prezenta executia algoritmului lui KRUSKAL pe un graf prezentat in paragraful anterior; muchiile desenate dublu vor apartine padurii A care este in crestere. Muchiile sunt considerate de catre algoritm ca fiind ordonate dupa ponderi. In figura se va prezenta o sageata care va reprezenta muchia luata in considerare la fiecare pas al algoritmului. Daca muchia uneste doi arbori distincti din padure, ea este adaugata la multimea A si este desenata dublu (cu doua linii) iar cei doi arbori sunt considerati impreuna.
a) se considera urmatorul graf [10]:
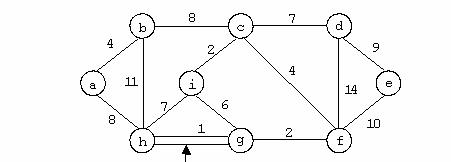
Dupa initializari si considerand ca |V| are un singur nod, se considera muchia de pondere cea mai mica (muchia (h, g) cu ponderea 1). Deoarece ea uneste doi arbori diferiti va fi adaugata la multimea A si se va desena prin dublare.
b) se considera acum o noua muchie de pondere minima (muchie usoara) si in cazul nostru este muchia (c, i) cu ponderea 2. Rezulta:
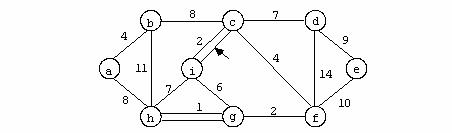
c) se considera urmatoarea muchie usoara (g, f) care poate fi adaugata la multimea A rezultand:
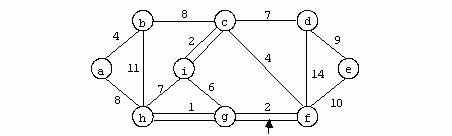
d) se considera urmatoarea muchie usoara (a, b) care este adaugata la multimea A. Rezulta figura de mai jos:
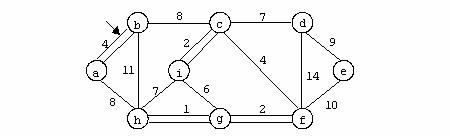
e) se considera urmatoarea muchie (c, f) din ordonarea facuta si poate fi adaugata si ea multimii A, rezultand:
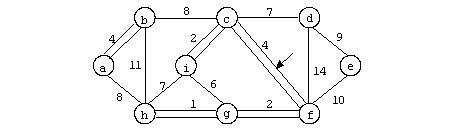
f) urmatoarea muchie luata in considerare este muchia (i, g) de pondere 6, dar adaugarea ei ar conduce la un ciclu (adica nodurile 'i' si 'g' fac parte din acelasi arbore), deci muchia (i, g) nu va fi adaugata la multimea A.
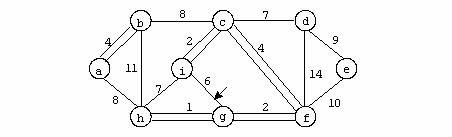
g) se considera muchia (c, d) cu ponderea 7 care poate fi adaugata la multimea A rezultand:
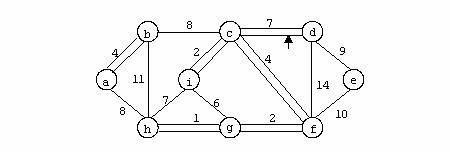
h) se considera urmatoarea muchie din ordonarea facuta, (i, h) de pondere 7 care, unind noduri din acelasi arbore, nu va fi adaugata la multimea A.
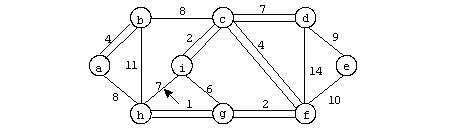
i) se considera muchia (a, h) care este adaugata la multimea A rezultand:
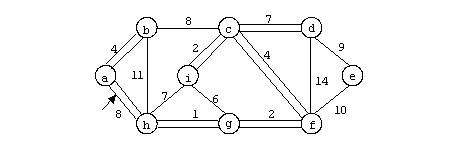
j) se considera muchia (b, c) care nu este adaugata la multimea A din motivele mai sus mentionate.
k) se considera muchia (d, e) care poate fi adaugata la multimea A. Rezulta urmatoarea figura:
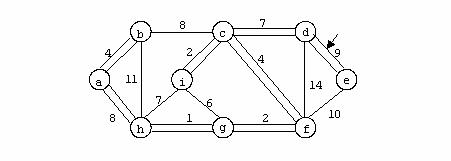
l) urmatoarea muchie (e, f) este cu ponderea 10 care nu poate fi adaugata multimii A conducand la ciclu.
m) se ia in considerare muchia (b, h) cu ponderea 11 care nici ea nu poate fi adaugata multimii A.
n) ultima muchie este (d, f) cu ponderea 14 care nici ea nu poate fi adaugata la multimea A.
Avand in vedere cele discutate in exemplul de mai sus si algoritmul in pseudocod prezentat, se poate rafina algoritmul lui KRUSKAL obtinandu-se urmatoarea descriere:
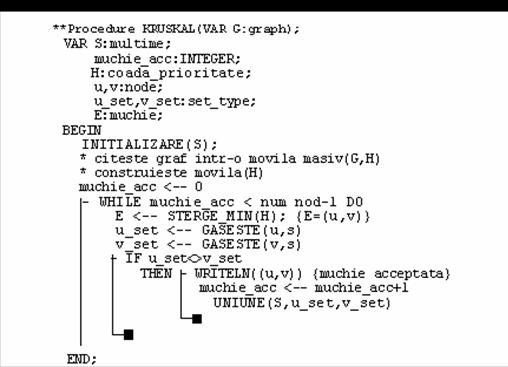
Se pot folosi de exemplu urmatoarele declaratii de tip:
Operatiile de baza asupra multimii disjuncte pot fi:

Algoritmul lui PRIM, ca si algoritmul lui KRUSKAL este un caz particular al algoritmului generic de determinare a arborelui de acoperire minima. Algoritmul lui PRIM are ca proprietate de baza faptul c muchiile din multimea A formeaza intotdeauna un singur arbore. Arborele porneste de la un nod arbitrar r considerat radacina si creste in timpul baleerii nodurilor grafului dat. La fiecare pas o muchie usoara care conecteaza un nod din multimea A cu un nod din multimea (VA) este adaugata la arborele care se construieste.
Conform corolarului din paragraful anterior, regula de adaugare a unei muchii (prezentata mai sus) la arborele ce se construieste furnizeaza o muchie sigura pentru multimea A si deci, cand algoritmul se va termina, muchiile multimii A formeaza un arbore de acoperire minima.
Desigur ca strategia algoritmului se bazeaza pe metoda de programare GREEDY, deoarece arborele creste la fiecare pas cu o muchie (muchia contribuie cu cea mai mica pondere posibila la un moment dat). Cheia implementarii algoritmului PRIM este aceea a selectarii unei muchii noi pentru a fi adaugata la arborele format de muchiile din multimea A.
In timpul executarii algoritmului, toate muchiile care nu se gasesc in arbore se afla intr-o coada de prioritate Q (care este construita luandu-se in considerare numai campul cheie). Pentru un nod v vom avea KEY v) care este ponderea minima a unei muchii care conecteaza nodul v la un nod din arborele care se construieste. Astfel, KEY(v)=¥ daca nu exista nici o astfel de muchie. Se noteaza prin PI(v) parintele nodului v din arborele care se construieste. In timpul executiei algoritmului, multimea A data in algoritmul GENERIC -ARB -ACOP -MIN este A= -Q) . Cand algoritmul se termina coada de prioritati Q este goala si multimea A contine arborele de acoperire minima a grafului G, adica: A=
Urmatoarea procedura prezinta algoritmul lui PRIM:

Primele linii initializeaza coada de prioritati Q cu toate nodurile grafului, iar cheia pentru fiecare nod devine infinit, cu exceptia cheii pentru radacina care devine zero. Parintele radacinii este initializat la NIL deoarece radacina arborelui nu are parinte. De-a lungul actiunii algoritmului, multimea (VQ) contine noduri din arborele ce se construieste.
Functia EXTRACT-MIN(Q) identifica nodul u din Q incident la o muchie usoara ce traverseaza o taietura (VQ, Q) (cu exceptia primei iteratii unde nodul 'u' este nod radacina). Se sterg nodurile din Q care se adauga la arborele ce se construieste. In continuare se actualizeaza campurile KEY si PI pentru fiecare nod v adiacent nodului u care insa nu este in arbore. Aceste actualizari sunt realizate pentru a se mentine invariantii buclei si avem: KEY(v)=W(v, PI(v)) iar muchia (v, PI(v)) este muchie usoara care conecteaza nodul v la un nod oarecare din arbore.
Performantele algoritmului PRIM depind de modul de implementare a structurii de date 'coada de prioritati'. Daca coada Q este implementata ca o movila binara se poate folosi algoritmul CONSTRUIESTE-MOVILA pentru a executa initializarea intr-un timp O(|V|). Bucla WHILE din algoritm este executata de |V| ori si deoarece fiecare operatie EXTRACT-MIN consuma un timp O(log|V|), timpul total pentru apelul rutinei EXTRACT-MIN este |V|log|V|).
Bucla interioara FOR este executata de O(|E|) ori, deoarece suma lungimilor pentru toate listele de adiacenta este 2.|E|. Testul pentru apartenenta la coada de prioritati Q (instructiunea IF) poate fi implementat in timp constant ca de exemplu: - se pastreaza un bit pentru fiecare nod care ne arata daca el se afla sau nu in coada Q (se actualizeaza bitul cand nodul este sters din coada).
Ultima
asignare implica o operatie de decrementare a cheii, care poate
fi implementata cu o movila binoma intr-un timp O(log|V|). Timpul total
pentru algoritmul PRIM este O(|V|log|V| + |E|log|V|) = O(|E|log|V|) care tinde
asimptotic spre timpul consumat de algoritmul KRUSKAL.
Exemplu
Se considera executia algoritmului PRIM pe graful din exemplul anterior. Se considera radacina arborelui ca fiind nodul a, muchiile din arborele ce se construieste sunt prezentate ca fiind duble iar nodurile construite la un moment dat sunt reprezentate in desen prin dreptunghiuri.
La fiecare pas al algoritmului, nodurile din arbore determina o taietura din graf, iar muchia usoara traverseaza taietura, deci poate fi adaugata la arborele ce se construieste. De exemplu in a treia figura de mai jos algoritmul are de ales intre doua muchii usoare (b, c) sau (a, h) care au amandoua ponderea 8 si care traverseaza taietura din graf.
a) Se porneste de la urmatoarea structura:
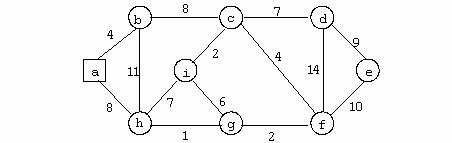
b) muchia usoara care traverseaza taietura este muchia (a, b) ce are ponderea 4, deci nodul 'b' se detaseaza pentru a se adauga la arborele ce se construieste si muchia (a, b) se dubleaza. Avem urmatoarea reprezentare:
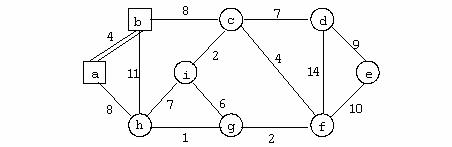
c) se alege muchia (b, c). Rezulta urmatoarea figura:
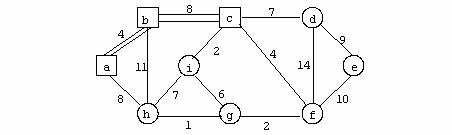
d) se alege muchia (c, i). Avem reprezentarea urmatoare:
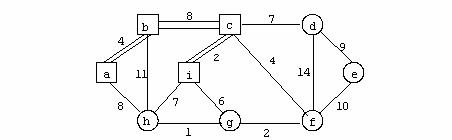
e) se alege muchia (c, f). Avem:
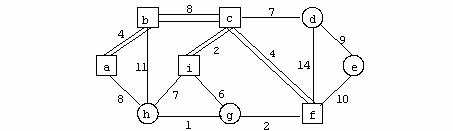
f) se alege muchia (f, g). Se obtine figura de mai jos:
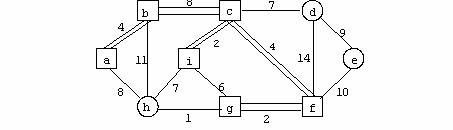
g) se alege muchia (g, h). Rezulta urmatoarea situatie:
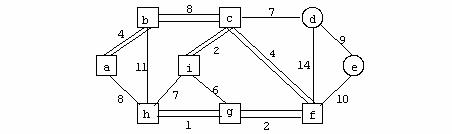
h) se alege muchia (c, d). Avem figura:
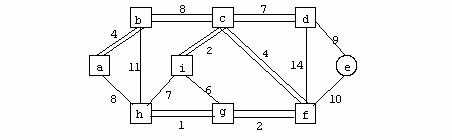
i) se alege muchia (d, e). Avem figura:
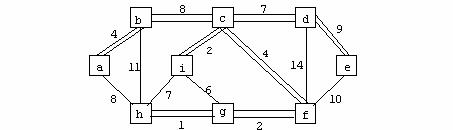
Se prezinta implementarea in limbajul C a algoritmilor din acest paragraf:
Urmatorul program realizeaza implementarea algoritmului Kruskal.
#include <stdio.h>
#define MAX_NOD 10
#define MAX_MUCHII 20
/* structura urmatoare implementeaza o movila care va contine muchiile grafului G*/
typedef struct h heap;
int G[MAX_NOD][MAX_NOD], /* matricea de adiacenta a grafului */
nr_el; /* numarul de noduri din graf */
void MAKEHEAP(int G[MAX_NOD][MAX_NOD],int nr_nod,
heap H[], int *nr_elheap)
for(i=nel / 2; i>=0; i--)
else
break;
}
else if(pz1 < nel)
break;
else
break;
}
}
*nr_elheap=nel;
return;
void DELETE_MIN(heap H[], int *nr_elheap, int *u, int *v)
else if(pz1 < *nr_elheap)
else
break;
}
if(pz1 >= *nr_elheap && pz2 >=*nr_elheap )
else cont=0;
}
else cont=0;
}
}
(*nr_elheap)--;
return;
void INITIALIZARE(int S[], int Dim)
int FIND(int x, int S[])
void
void KRUSKAL(int G[MAX_NOD][MAX_NOD], int nr_noduri)
}
return;
int main()
Urmatorul program implementeaza algoritmul lui PRIM.
#include <stdio.h>
#include <values.h>
#define NMAX 20
typedef struct rec qrec;
int graf[NMAX][NMAX]; // matricea de adiacenta a grafului
int w[NMAX][NMAX]; // matrice in care se
// pastreaza ponderile muchiilor
int n; // numarul de noduri din graf
int r; // radacina arborelui de acoperire
int PI[NMAX];
void PRIM(int graf[NMAX][NMAX], // matricea de incidenta a grafului
int w[NMAX][NMAX], // matrice in care se
// pastreaza ponderile muchiilor
int n, // numarul de noduri din graf
int r, // radacina arborelui de acoperire
int PI[NMAX])
else
nQ=n;
PI[r]=-1;
while(nQ)
}
}
}
int main()
}
printf('Radacina arborelui de acoperire r=');
fscanf(f, '%d', &r);
PRIM(graf, w, n, r, PI);
for(i=0;i<n;i++)
printf('%d', PI[i]);
return 0;
7 Algoritmii DIJKSTRA si BELLMAN-FORD
Se considera cazul unui motociclist care doreste sa gaseasca ruta cea mai scurt posibila dintre doua localitati. Se considera ca el poseda o harta a regiunii pe care sunt marcate distantele dintre fiecare pereche de intersectii adiacente si se considera problema determinarii celei mai scurte rute. O prima abordare este aceea a enumerarii tuturor rutelor dintre cele doua localitati si sa se selecteze cea cu distanta cea mai mica.
Se observa usor ca si in cazul in care se cere ca sa nu existe rute cu cicluri, exista un numar mare de posibilitati, unele dintre ele nu pot fi luate in considerare fiind evident rute ocolitoare.
Se va prezenta un mod de rezolvare eficient pentru o astfel de problema si acest mod este dat de problema celor mai scurte drumuri cu o singura sursa.
Se considera dat un graf orientat G=(V, E) cu o functie reala de ponderare a muchiilor W:E R (care poate fi asimilata distantelor dintre doua puncte). Daca se considera un drum p=<v0, v1, , vk>, atunci ponderea drumului p este data de suma ponderilor ce-l constituie, adica:
W(p)= ![]()
Se defineste ponderea drumului cel mai scurt de la nodul u la nodul v astfel:
DEL(u,v)=
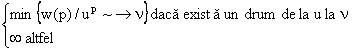
Un cel mai scurt drum de la nodul u la nodul v, este definit ca un drum oarecare p a carui pondere W(p)=DEL(u, v).
In problema motociclistului se poate modela harta ca un graf, nodurile reprezentand intersectiile, muchiile reprezentand drumurile si ponderile muchiilor reprezentand distantele de drumuri.
Exista si alte posibilitati de reprezentare a ponderilor: de exemplu prin unitati de timp sau cost, sau penalizari, sau alte cantitati care pot fi acumulate liniar in timp si pentru care se doreste sa se gaseasca un minim.
Observatie
Algoritmul de parcurgere in latime a unui graf (BFS) este un algoritm de gasire a celor mai scurte drumuri ce lucreaza pentru grafuri neponderate (grafurile in care fiecare muchie poate fi considerata ca avand ponderea unitate).
Problema drumurilor cele mai scurte cu o singura sursa se poate defini astfel: dandu-se graful G=(V, E), se doreste sase gaseasca drumul cel mai scurt de la un nod sursa dat, sIV la fiecare nod vIV.
Exista o serie de probleme ce pot fi rezolvate cu ajutorul algoritmului pentru problema drumului cel mai scurt cu o singura sursa, ca de exemplu:
a) problema drumurilor cele mai scurte cu o singura destinatie - se considera un nod dat d care este destinatia drumului si se cauta cel mai scurt drum ce porneste de la fiecare nod vIV. Se vede ca prin inversarea directiei muchiilor din graful dat, aceasta problema se reduce la o problema cu o singura sursa.
b) problema celui mai scurt drum cu o singura pereche - se considera doua noduri oarecare u, vIV si se cere sa se gaseasca cel mai scurt drum de la nodul u la nodul v. Se vede ca daca se rezolva problema pentru o singura sursa, considerand nodul u nod sursa se rezolva si aceasta problema. Se poate arata ca nu exista nici un algoritm cunoscut pentru aceasta problema care sa ruleze asimptotic mai repede decat algoritmul pentru problema cu o singura sursa, considerand cazul cel mai devaforabil.
c) problema celui mai scurt drum pentru toate perechile - regasirea drumului cel mai scurt de la nodul u la nodul v pentru fiecare pereche de noduri (u, v) din multimea V. Aceasta problema poate fi rezolvata ruland algoritmul pentru o singura sursa, o data pentru fiecare nod, dar problema poate fi rezolvata mai bine (problema insasi este interesanta pentru a fi cercetata).
Pentru anumite intrari ale unor aplicatii, pentru problema drumului cel mai scurt cu o singura sursa pot exista muchii ale caror ponderi sunt negative. Daca graful G=(V, E) nu contine cicluri cu pondere negativa care pot fi atinse din nodul sursa s, atunci pentru orice nod vIV, ponderea celui mai scurt drum DEL(s, v) ramane bine definita chiar daca ea are o valoare negativa.
Daca exista un ciclu cu pondere negativa care poate fi atins din s atunci ponderile drumurilor cele mai scurte nu sunt bine definite, adica nici un drum de la nodul s la un nod din ciclu nu poate fi cel mai scurt drum. Daca exista cicluri cu o pondere negativa, pe astfel de drumuri, de la nodul sursa s la nodul v se defineste DEL(s, v) = -¥
Exemplu
Figura urmatoare ilustreaza efectul ponderilor negative pentru ponderea celui mai scurt drum [10]. Se considera un graf cu 11 noduri - in fiecare nod este aratata ponderea celui mai scurt drum de la nodul sursa s. Deoarece nodurile e si f formeaza un ciclu cu pondere negativa si care poate fi atins din nodul s se vor nota ponderile celor mai scurte drumuri pentru nodurile respective ca fiind - ¥
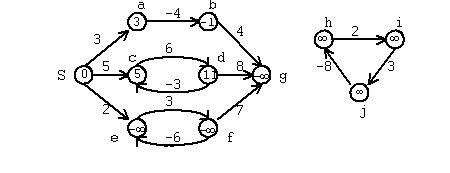
Deoarece nodul g este atins dintr-un nod a carui pondere a celui mai scurt drum de la nodul sursa la el este -¥ va primi si el (nodul g) o pondere a celui mai scurt drum egala cu -¥.
Nodurile h, i si j ale grafului nu pot fi atinse din nodul sursa s si din acest motiv ponderile celui mai scurt drum de la nodul sursa la fiecare din ele sunt +¥ (chiar daca ele se afla intr-un ciclu cu pondere negativa). Deoarece exista un singur drum de la nodul s la nodul a, dat de muchia (s, a), rezulta ca:
DEL(s, a)=W(s, a)=
Similar, exista un singur drum de la nodul s la nodul b si putem calcula:
DEL(s, b) = W(s, a)+W(a, b)=3+(-4)=(-1).
Exista o infinitate de drumuri de la nodul s la nodul c si anume: (s, c), (s, c, d, c), (s, c, d, c, d, c) s.a.m.d. Deoarece ciclul (c, d, c) are o pondere pozitiva (6+(-3)=3) rezulta ca cel mai scurt drum de la nodul s la nodul c este dat de muchia (s, c) care are DEL(s, c)=5.
Similar cel mai scurt drum de la nodul s la nodul d este (s, c, d) cu ponderea
DEL(s,d)=W(s, c)+W(c, d)=11.
Analog exista o infinitate de drumuri de la nodul s la nodul e care sunt (s, e), (s, e, f, e), (s, e, f, e, f, e), s.a.m.d. Deoarece ciclul (e, f, e) are ponderea negativa (3+(-6)=(-3)), nu exista un cel mai scurt drum de la nodul s la nodul e. Prin traversarea ciclului cu pondere negativa (s, e) de un numar arbitrar de ori, se poate gasi un drum de la nodul s la nodul e cu o pondere arbitrar de mica si din acest motiv DEL(s, e)= -¥ . Similar DEL(s, f)= -¥
Deoarece nodul g poate fi atins din nodul s, se pot gasi de asemenea drumuri cu ponderi negative arbitrar de mari de la nodul s la nodul g, si de aceea DEL(s, g)= -¥
Nodurile h, i si j formeaza de asemenea un ciclu cu pondere negativa dar nu pot fi atinse din nodul s rezultand DEL(s, h)=DEL(s, i)=DEL(s, j)=+¥
Observatie
O serie de algoritmi pentru determinarea drumurilor cele mai scurte ca de exemplu algoritmul lui DIJKSTRA presupune ca toate ponderile muchiilor din graful de intrare sunt pozitive (ca in exemplul hartilor rutiere). Alti algoritmi ca de exemplu algoritmul lui BELLMAN-FORD permit existenta muchiilor cu ponderi negative in graful initial si furnizeaza un raspuns corect atata timp cat nu exista cicluri cu ponderi negative care sa fie atinse din nodul sursa (daca exista astfel de cicluri cu pondere negativa, algoritmul le detecteaza si raporteaza existenta lor).
Se poate dori sa se calculeze nu numai ponderea celui mai scurt drum dar si nodurile de pe acest drum. De fapt, reprezentarea celui mai scurt drum este similara cu reprezentarea pentru arborii in latime [9] (prezentata la algoritmul BFS).
Se considera un graf dat G=(V, E) si pentru fiecare nod vIV se considera ca PI(v) noteaza predecesorul nodului v (in cazul in care nu exista predecesor, PI(v)=NIL). Algoritmul pentru cel mai scurt drum pune valoarea PI pe nodul care formeaza un lant al predecesorilor nodului v astfel incat mergand inapoi de-a lungul lantului sa se determine cel mai scurt drum de la nodul s la nodul v. Dandu-se un nod v pentru care PI(v)¹NIL procedura PRINT-CALE(G,s,v) poate fi utilizata pentru tiparirea celui mai scurt drum de la nodul s la nodul v.
In timpul executiei algoritmului pentru cel mai scurt drum, valorile PI nu sunt necesare sa fie indicate. Ca si in algoritmul de parcurgere in latime se pune in evidenta subgraful predecesor Gp=(Vp, Ep) care este indus de valorile PI. Se defineste din nou multimea nodurilor Vp ca fiind multimea nodurilor din graful dat pentru care predecesorul este diferit de valoarea NIL plus sursa s, adica: Vp=È. Muchiile orientate din multimea Ep formeaza multimea muchiilor induse din valori PI(v) pentru nodurile din Vp adica:
Ep=
Se va demonstra ca valorile PI produse de algoritm au proprietatea ca la terminare subgraful Gp contine arborele drumurilor cele mai scurte, adica arborele care contine drumul cel mai scurt de la nodul sursa s la fiecare nod care poate fi atins din nodul s. Arborele drumurilor cele mai scurte este asemanator cu arborele in latime, dar el contine drumurile cele mai scurte, de la nodul sursa la un nod oarecare, definite in termenii ponderilor muchiilor in locul numarului de muchii pentru arborele in latime.
Fie G=(V, E) un graf dat orientat si ponderat. Se considera o functie de ponderare W:E R si se presupune ca G nu contine cicluri cu ponderi negative care pot fi atinse din nodul sursa sIV (adica drumurile cele mai scurte sunt bine definite).
Un arbore pentru cele mai scurte drumuri cu radacina s, este un subgraf orientat G'=(V', E') unde V' V, E' E astfel incat:
1) V' este multimea nodurilor din G care pot fi atinse din nodul s
2) G' formeaza un arbore cu radacina s
3) pentru orice nod vIV', un drum simplu unic de la nodul s la nodul v in arborele G', este un drum cel mai scurt de la nodul s la nodul v in graful G.
Observatie
Drumurile cele mai scurte nu sunt in mod necesar unice.
Exemplu
Umatoarea figura arata situatia unui graf orientat ponderat care prezinta doi arbori cu cele mai scurte drumuri de aceeasi radacina. Prima figura prezinta graful orientat ponderat dat si nodul sursa s. Celelalte doua figuri prezinta arborii cu drumurile cele mai scurte prin dublarea muchiilor.
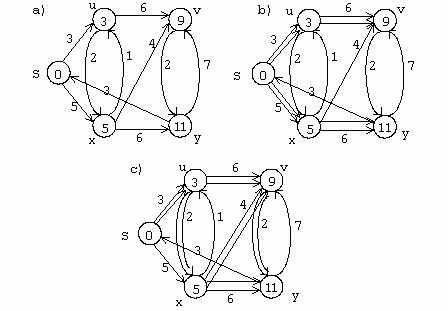
Observatie
Pentru a intelege algoritmii pentru cele mai scurte drumuri cu o singura sursa, este necesar sa se inteleaga tehnicile folosite si proprietatile celor mai scurte drumuri. Tehnica principala folosita de algoritm este numita metoda relaxarii care descreste in mod repetat marginea superioara a ponderii drumului cel mai scurt considerat la un moment dat, pentru fiecare nod pana cand marginea superioara devine egala cu ponderea celui mai scurt drum.
In continuare se va arata cum actioneaza aceasta metoda a relaxarii si se vor prezenta o serie de proprietati ale ei.
O proprietate tipica pentru drumurile cele mai scurte, care este exploatata de algoritmii ce vor fi prezentati, este aceea a faptului ca subdrumurile din cele mai scurte drumuri sunt de asemenea cele mai scurte drumuri. Aceasta proprietate de substuctura optimala este un indicator atat pentru aplicabilitatea programarii dinamice cat si pentru metoda GREEDY.
Urmatoarea propozitie si corolarul ei afirma proprietatea de substructura optimala, in mod mai precis.
Propozitie
(Subdrumurile drumurilor cele mai scurte sunt drumuri cele mai scurte).
Se considera dat un graf orientat, ponderat G=(V, E) si o functie de ponderare W:E R. Se considera p un drum de la nodul v1 la nodul vk unde p=<v1, v2, , vk> este cel mai scurt drum intre nodurile v1 si vk. Se considera doi indici i si j astfel incat 1£i£j£k si se considera subdrumul pij intre doua noduri vi si vj astfel: pij=<vi, vi+1, , vj> (unde pij este un subdrum al celui mai scurt drum p). Atunci pij este cel mai scurt drum intre nodurile vi si vj.
Demonstratie
Se considera o descompunere a drumului p pentru a pune in evidenta subdrumul pij astfel:
![]()
Rezulta urmatoarea relatie de calcul pentru ponderea drumul p:
W(p)=W(p1i)+W(pij)+W(pjk).
Se presupune prin reducere la absurd ca exista un drum pij' de la nodul vi la nodul vj cu o pondere mai mica decat a drumului pij adica: W(pij') < W(pij). Rezulta ca exista o alta descompunere a drumului p care pune in evidenta drumul pij' intre nodurile vi si vj astfel:
![]()
De aici rezulta ca se poate scrie pentru ponderea drumului p urmatoarea relatie:
W'(p)=W(p1i)+W(pij')+W(pjk)<W(p)
ceea ce contrazice ipoteza ca p este cel mai scurt drum intre nodurile v1 si vk.
Corolar
Fie G=(V, E) un graf ponderat orientat cu functia de ponderare W:E R. Se presupune ca cel mai scurt drum, p, de la nodul sursa s la un nod v poate fi descompus astfel:
![]()
(pentru un nod oarecare u si un drum oarecare p')
Atunci ponderea celui mai scurt drum de la nodul s la un nod v este:
DEL(s, v)=DEL(s, u)+W(u, v).
Demonstratie
Din Propozitie subdrumul p' este cel mai scurt drum de la nodul sursa s la nodul u. Rezulta:
DEL(s, v)=W(p)=W(p')+W(u, v)=DEL(s, u)+W(u, v).
Urmatoarea lema prezinta o proprietate, simpla dar folositoare, cu privire la ponderile celor mai scurte drumuri.
Lema
Fie G=(V, E) un graf ponderat orientat cu functia de ponderare W:E R si se considera s nodul sursa. Atunci pentru orice muchie (u, v)IE se poate scrie:
DEL(s, v)£DEL(s, u)+W(u, v).
Demonstratie
Fie p un cel mai scurt drum de la nodul s la nodul v care nu are o pondere mai mare decat oricare alt drum de la nodul s la nodul v. Drumul p nu are o pondere mai mare decat un drum particular care considera cel mai scurt drum de la nodul sursa s la un nod u oarecare la care se adauga ponderea muchiei (u, v) (conform Propozitiei).
Algoritmii care se vor prezenta in continuare folosesc metoda relaxarii. Pentru fiecare nod vIV se considera un atribut d(v) care reprezinta marginea superioara a ponderii unui cel mai scurt drum de la nodul sursa la nodul v. Din acest motiv valoarea d(v) se numeste pondere estimata a celui mai scurt drum. Mai intai trebuie sa se initializeze ponderile estimate pentru cele mai scurte drumuri precum si nodurile predecesoare de pe acestea si se considera urmatorul algoritm:

Dupa initializarea predecesorului fiecarui nod din graf cu valoarea NIL, se initializeaza ponderea estimata pentru nodul sursa cu zero, iar pentru celelalte noduri din graf cu ¥
Procesul de relaxare a unei muchii, (u, v) din graf consta in testarea faptului daca se poate imbunatati drumul cel mai scurt catre nodul v care trece prin nodul u prin actualizarea ponderii estimate d(v) si a predecesorului PI(v). Un pas de relaxare va decrementa valoarea estimata d v a unui cel mai scurt drum si actualizeaza campul predecesor pentru nodul v, adic campul PI(v).
Urmatorul algoritm executa un pas de relaxare asupra unei muchii oarecare (u, v) din graf.
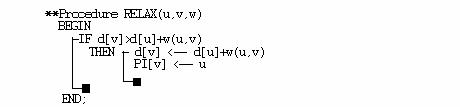
Exemplu
Urmatoarea figura [10] arata doua exemple ale unui pas de relaxare aplicat asupra unei muchii. Prima arata cum ponderea scade, iar cea de-a doua figura demonstreaza faptul ca ponderea ramane neschimbata.
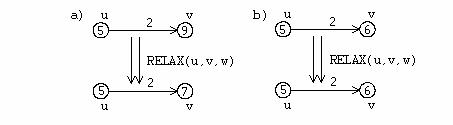
a) deoarece d(v)>d(u)+W(u, v) inainte de aplicarea rutinei de relaxare rezulta ca valoarea estimata d(v) descreste.
b) deoarece valoarea estimata d(v)£d(u)+W(u, v) inainte de executia pasului de relaxare, rezulta d(v) ramane neschimbata in urma relaxarii.
Algoritmii care vor fi prezentati in continuare vor folosi in mod repetat operatia de relaxare a unor muchii din graf. In urma operatiei de relaxare se pot schimba ponderile estimate si predecesorii nodurilor, considerati la un moment dat. Algoritmii difera prin numarul de aplicatii ale procesului de relaxare asupra muchiilor.
In algoritmul lui DIJKSTRA, pentru gasirea celor mai scurte drumuri cu o singura sursa intr-un graf orientat aciclic, se aplica o singura data algoritmul de relaxare pentru fiecare muchie din graf.
In algoritmul BELLMAN-FORD fiecare muchie este relaxata de mai multe ori.
Corectitudinea algoritmilor depinde foarte mult de proprietatile operatiei de relaxare si pentru aceasta se vor enunta cateva proprietati. Acestea descriu rezultatul executiei unei secvente de pasi de relaxare aplicati asupra unor muchii intr-un graf orientat ponderat care a fost initializat cu algoritmul INIT- SINGURA-SURSA.
Lema
Fie G=(V, E) un graf ponderat, orientat, cu functia de ponderare W:E R si o muchie oarecare (u, v)IE. Atunci imediat dupa aplicarea unei relaxari asupra muchiei (u, v) printr-un apel RELAX(u, v, w), rezulta d(v)£d(u)+W(u, v).
Demonstratie
Daca inaintea relaxarii muchiei, avem d(v)>d(u)+W(u, v) atunci in urma relaxarii vom avea:
(v)=d(u)+W(u, v).
Daca insa inainte avem: d(v)£d(u)+W(u, v) atunci dupa relaxare nici d(u) nici d(v) nu se modifica, deci si dupa relaxare avem relatia:
d(v)£d(u)+W(u, v).
Lema
Fie G=(V, E) un graf ponderat orientat cu functia de ponderare W:E R si fie sIV un nod sursa si se considera ca s-a executat algoritmul INIT-SINGURA-SURSA (G, s).
Atunci d(v)³DEL(s,v) pentru toate nodurile vIV si aceasta relatie este un invariant pentru orice secventa de pasi de relaxare care se aplica muchiilor din graful G. Mai mult, o data ce valoarea d(v) atinge cea mai scazuta margine care este DEL(s,v) ea nu se mai schimba niciodata.
Demonstratie
Relatia invarianta d(v)³DEL(s,v) este desigur adevarata dupa initializare deoarece d(s)=0³DEL(s,s); (DEL(s,s) este -¥ in cazul in care s se afla pe un ciclu cu pondere negativa sau este zero in celelalte cazuri). Apoi pentru celelalte noduri avem: d(v)= +¥ ceea ce implica d(v)³DEL(s,v) pentru orice nod vI(V
Se va demonstra in continuare prin reducere la absurd si fie v primul nod pentru care un pas de relaxare aplicat asupra muchiei (u,v) ar conduce la relatia d(v)<DEL(s,v). Atunci imediat dupa aplicarea algoritmului de relaxare asupra muchiei (u,v) se poate scrie:
d(u)+W(u,v)=d(v)<DEL(s,v)£DEL(s,u) +W(u,v)
(conform Lemei anterioare).
De aici rezulta d(u)<DEL(s,u).
Deoarece operatia de relaxare aplicata muchiei (u,v) nu schimba valoarea lui d(u) inegalitatea de mai sus trebuie sa fie indeplinita exact inaintea aplicarii operatiei de relaxare asupra muchiei (u,v) ceea ce contrazice alegerea ca v este primul nod pentru care d(v)£DEL(s,v). Din aceasta contradictie rezulta d(v)³DEL(s,v) pentru orice vIV.
Pentru a vedea ca valoarea d(v) nu se modifica dupa ce s-a atins valoarea d(v)=DEL(s,v) (adica dupa ce s-a atins cea mai scazuta margine) trebuie sa aratam ca d(v) nu poate descreste deoarece d(v)³DEL(s,v) si se stie ca nu poate sa creasca, deoarece in urma pasilor de relaxare valoarea estimata d nu creste niciodata.
Corolar
Se considera dat un graf orientat ponderat G=(V, E) si functia de ponderare W:E R si se considera ca nu exista nici un drum care sa uneasca nodul sursa sIV cu un nod oarecare vIV.
Atunci dupa ce graful este initializat cu algoritmul INIT-SINGURA-SURSA (G,s) avem d(v)=DEL(s,v) si aceasta relatie se mentine ca invariant pentru orice secventa de pasi de relaxare ce se aplica muchiilor din G.
Demonstratie
Din Lema avem d(v)³DEL(s,v) dar neexistand nici un drum intre nodurile s si v rezulta:
EL(s,v)=¥ deci d(v)=¥=DEL(s,v) .
Urmatoarea lema este foarte importanta in demonstrarea corectitudinii algoritmului pentru gasirea drumurilor cele mai scurte cu o singura sursa. Ea furnizeaza conditiile suficiente ca operatia de relaxare sa impuna ca valorile ponderilor estimate sa convearga catre valoarea ponderii drumului cel mai scurt.
Lema
Se
considera dat un graf, orientat, ponderat G=(V, E) si functia de ponderare W:E R si fie sIV nod sursa si se considera cel mai scurt drum dintre nodurile s si v dat
de: s u v pentru doua noduri oarecare u,vIV.
Se presupune ca graful G este initializat de algoritmul INIT-SINGURA-
SURSA(G,s).
Atunci o secventa de pasi de relaxare care implica apelurile RELAX(u,v,W) este executata asupra muchiilor grafului dat G. Daca d(u)=DEL(s,u) la orice moment de timp inainte de apel, atunci rezulta d(v)=DEL(s,v) la orice moment de timp dupa apel.
Demonstratie
Din Lema anterioara daca d(u)=DEL(s,u) inainte ca operatia de relaxare sa se execute asupra muchiei (u,v) atunci aceasta egalitate se pastreaza si dupa executarea operatiei de relaxare. In particular, dupa relaxarea muchiei (u,v) avem:
d(v)£d(u)+W(u,v)=DEL(s,u)+W(u,v)=DEL(s, v).
(conform Lemelor si Corolarului anterior)
Din Lema anterioara rezulta ca DEL(s,v) margineste valoarea d(v) si se poate trage concluzia ca d(v)=DEL(s,v). Rezulta ca egalitatea se va mentine si dupa aplicarea algoritmului de relaxare.
Deci operatia de relaxare conduce la descresterea monotona a valorii estimate pentru cele mai scurte drumuri catre ponderea precisa a celui mai scurt drum.
Ar fi bine sa se arate ca o data ce o secventa de relaxari a fost calculata pentru ponderile celui mai scurt drum, subgraful predecesor Gp care este indus de valorile rezultate pentru campurile PI, contine arborele celor mai scurte drumuri pentru graful G dat.
Urmatoarea lema arata ca subgraful predecesor Gp formeaza intotdeauna un arbore a carui radacina este nodul sursa al celui mai scurt drum.
Lema
Se considera dat un graf, orientat, ponderat G=(V, E) si functia de ponderare W:E R si fie sIV nod sursa, si se presupune ca graful G nu contine cicluri cu pondere negativa care sa poata fi atinse pornind din nodul s.
Atunci dupa ce graful este initializat prin INIT-SINGURA-SURSA(G,s) subgraful predecesor Gp formeaza un arbore cu radacina "s" si orice secventa de pasi de relaxare aplicata asupra muchiilor lui G, mentine aceasta proprietate ca un invariant.
Demonstratie
Initial numai nodul sursa se afla in subgraful Gp si deci lema este evident adevarata.
Se
considera acum subgraful predecesor Gp obtinut dupa o secventa de
pasi de relaxare. Se va arata mai intai ca Gp este aciclic prin
reducere la absurd si se presupune ca dupa un anumit pas de relaxare se creeaza
un ciclu in graful Gp. Acest ciclu este c=<v0, v1,
, vk> unde v0=vk. Atunci PI(vi)=vi-1
oricare ar fi iI![]() .
.
Se presupune fara sa se piarda din generalitate ca se aplica relaxarea asupra muchiei (vk-1, vk) si se obtine un ciclu in Gp. Se afirma acum ca toate nodurile ciclului "c" astfel considerat pot fi atinse din nodul sursa "s". Din cele considerate mai sus rezulta ca fiecare nod din ciclul c are un predecesor deoarece PI¹NIL. Astfel, fiecarui nod ce apartine ciclului c i s-a asignat o valoare estimata finita, cand i s-a asignat o valoare PI¹NIL.
Din Lema anterioara rezulta ca fiecare nod din ciclul c are o pondere finita pentru cel mai scurt drum, ceea ce implica faptul ca fiecare nod al ciclului poate fi atins din nodul sursa s. Se vor examina valorile estimate pentru nodurile din ciclul c exact inaintea apelului RELAX(vk-1, vk, W) si se va arata ca c este un ciclu cu pondere negativa (ceea ce contrazice ipoteza ca G nu contine cicluri cu pondere negativa, care sa fie atinse pornind din nodul sursa).
Inainte de apel avem PI(vi)=vi-1 pentru orice i=1, 2, , (k-1). Astfel pentru i=1, 2, , (k-1) ultima actualizare a valorii d(vi) a fost executata prin asignarea:
d(vi) d(vi-1)+W(vi,vi-1).
Daca d(vi-1) s-a schimbat, atunci ea a scazut.
Deci exact inainte de apelul RELAX(vk-1,vk,W) avem:
d(vi)³d(vi-1)+W(vi,vi-1) oricare ar fi i=1, 2, , (k-1). (3)
Deoarece PI(vk) s-a schimbat in urma apelului rezulta ca avem urmatoarea inegalitate stricta:
d(vk)>d(vk-1)+W(vk-1,vk).
Aceste inegalitati se aduna cu inegalitatea (3) si se obtin urmatoarele sume pentru valorile estimate in cadrul nodurilor ciclului c.
![]()
dar avem
![]()
deoarece fiecare nod din ciclul c apare exact odata in fiecare suma. Aceasta implica
![]()
adica suma ponderilor muchiilor ciclului c este negativa, ceea ce este o contradictie.
S-a demonstrat pana acum ca Gp este un graf orientat aciclic. Pentru a arata ca el formeaza un arbore cu radacina s este suficient sa demonstram ca pentru fiecare nod vIVp exista un drum unic de la nodul s la nodul v in subgraful Gp.
Trebuie sa aratam mai intai ca exista un drum de la nodul s la fiecare nod din Vp. Nodurile din Vp sunt acelea pentru care valoarile PI sunt diferite de NIL si in plus exista nodul sursa s. Ideea de demonstrare este aceea a inductiei pentru a arata ca exista un drum de la nodul s la orice nod din Vp (lucru lasat ca exercitiu).
Pentru completarea demonstratiei trebuie sa se arate ca pentru orice vIVp exista cel mult un drum de la nodul s la nodul v in subgraful Gp.
Se presupune prin reducere la absurd ca exista doua drumuri simple de la nodul s la nodul v. Fie acestea drumurile: p1 care poate fi descompus in s u x z v si p2 ce poate fi descompus in s u y z v, unde x¹y.
Aceasta situatie se reprezinta schematic in urmatoarea figura:
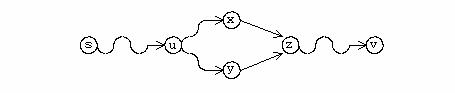
Dar PI(z)=x si PI(z)=y ceea ce contrazice faptul ca x¹y de unde rezulta faptul ca exista un drum simplu unic in subgraful Gp de la nodul s la nodul v si deci Gp formeaza un arbore cu nodul radacina s.
Se poate acum arata ca dupa ce a fost executata o secventa de pasi de relaxare si dupa ce tuturor nodurilor li s-a asignat ponderea 'adevarata' a drumului cel mai scurt atunci subgraful predecesor Gp este un arbore al celor mai scurte drumuri.
Lema
Fie G=(V, E) un graf orientat ponderat cu functia de ponderare W:E R. Se considera nodul s nodul sursa si se presupune ca G nu contine cicluri cu ponderi negative ce pot fi atinse din nodul sursa s. Se presupune ca se apeleaza procedura INIT-SINGURA-SURSA(G,s) si apoi se executa o secventa oarecare de pasi de relaxare asupra muchiilor din G care produc d(v)=DEL(s,v) pentru orice vIV. Atunci subgraful predecesor Gp este arborele drumurilor cele mai scurte cu radacina s.
Demonstratie
Trebuie sa demonstram ca cele trei proprietati ale arborelui drumurilor cele mai scurte se pastreaza si pentru submultimea Gp. Pentru a arata prima proprietate trebuie sa se demonstreze ca Vp este multimea nodurilor ce se pot atinge din s. Din definitie, ponderea celui mai scurt drum DEL(s,v) are o valoare finita daca si numai daca nodul v este atins din nodul sursa s. Astfel nodurile care sunt atinse din nodul s sunt acelea care au valori d finite. Dar unui nod vI(V ) i se asigneaza o valoare finita d(v) daca si numai daca PI(v)¹NIL. Astfel nodurile multimii Vp sunt exact acele noduri care sunt atinse din nodul sursa s.
A doua proprietate ce trebuie demonstrata rezulta imediat din Lema anterioara.
Ramane sa se demonstreze ultima
proprietate pentru arborele drumurilor cele mai scurte, adica pentru orice vIVp,
exista un drum unic simplu de la nodul s la nodul v notat ![]() in Gp care este cel mai scurt drum
de la nodul s la nodul v in graful G.
in Gp care este cel mai scurt drum
de la nodul s la nodul v in graful G.
Fie p=<v0, v1, , vk> unde v0=s si vk=v pentru i=1, 2, , k.
Avem d(vi)=DEL(s,vi) si d(vi)³d(vi-1)+W(vi-1,vi).
Rezulta:
W(vi-1,vi)£DEL(s,vi)-DEL(s,vi-1).
Se face suma de-a lungul drumului p rezultand ponderea pentru drumul p, adica:
![]()
W(p)==DEL(s,vk) - DEL(s,v0)=DEL(s,vk)
Ultima egalitate rezulta din faptul ca DEL(s,v0)=DEL(s,s)=0.
Rezulta deci ca W(p)£DEL(s,vk).
Deoarece DEL(s,vk) este marginea inferioara pentru ponderea oricarui drum de la nodul sursa s la un nod vk rezulta W(p)=DEL(s,vk). Rezulta deci ca p este cel mai scurt drum de la un nod s la un nod v oarecare.
Algoritmul lui DIJKSTRA rezolva problema drumurilor cele mai scurte cu o singura sursa pentru grafuri orientate, ponderate in cazul in care ponderile tuturor muchiilor sunt pozitive. Deci in acest caz se presupune ca W(u,v)³0 pentru orice muchie (u,v)IE.
Algoritmul lui DIJKSTRA utilizeaza o multime S a nodurilor a caror pondere finala pentru cel mai scurt drum de la nodul sursa la ele a fost deja determinat. Adica, pentru orice nod vIS avem d(v)=DEL(s,v), algoritmul selectand in mod repetat un nod uI(VS) cu valoarea ponderii estimate minima si insereaza nodul u in multimea S dupa care aplica operatia de relaxare asupra tuturor muchiilor ce pleaca din nodul u.
In algoritmul prezentat in pseudocod mai jos, se considera o coada de prioritate Q ce va contine toate nodurile din multimea (VS) dupa valorile d ale lor.
In algoritmul prezentat, graful G este considerat dat cu ajutorul listelor de adiacenta.

Prima linie a algoritmului executa initializarea obisnuita a grafului G, adica valoarea pentru ponderea estimata 'd' si pentru predecesorul PI. Urmatoarea linie initializeaza multimea S ce devine vida. Cealalta linie initializeaza coada de prioritate continand toate nodurile din multimea (V-S)=V-Æ=V.
La fiecare iteratie a buclei while un nod u este extras din Q=VS si inserat in multimea S. La prima iteratie avem u=s; nodul u are cea mai mica valoare estimata din nodurile ce se afla in multimea (VS).
Bucla FOR aplica relaxarea fiecarei muchii (u,v) care paraseste nodul u si astfel se actualizeaza valoarea estimata d(v) si campul predecesor PI(v), daca drumul cel mai scurt catre nodul v poate fi imbunatatit trecand prin nodul u.
Se observa faptul ca nodurile nu mai sunt niciodata inserate in Q dupa ce aceasta a primit toate nodurile grafului (linia a treia a algoritmului) si de asemenea, fiecare nod este scos din coada Q si inserat in multimea S exact o data. Deci bucla while se executa de exact de |V| ori.
Exemplu
Executia algoritmul lui DIJKSTRA este aratata in urmatoarele figuri, unde nodul sursa 's' este cel mai din stanga. Valoarea estimata la un moment dat este aratata in interiorul cerculetului, iar muchiile dublate indica valoarea predecesorului, adica daca muchia (u,v) este dublata atunci PI(v)=u. Nodurile reprezentate prin dreptunghi sunt cele ce se afla in S, iar cele in cercuri sunt cele ce se afla in Q=V-S.
Figura a) arata situatia exacta inaintea executiei buclei while.
Figura b) se obtine dupa o iteratie a buclei while.
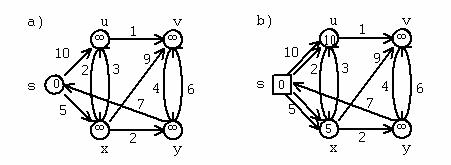
Nodul in patrat are valoarea 'd' minima si este ales drept nod u in linia a cincea a algoritmului DIJKSTRA.
Urmatoarele figuri arata situatia dupa fiecare iteratie a buclei WHILE. Nodurile in patrate, din fiecare figura sunt alese drept nod u pentru urmatoarea iteratie. Valorile 'd' si PI reprezentate in figura f) sunt valori finale.
Avem:
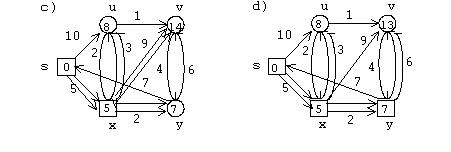
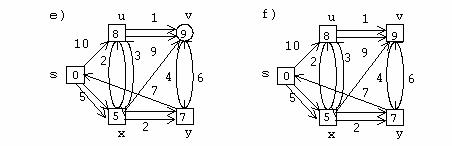
Observatie
Deoarece algoritmul lui DIJKSTRA gaseste intotdeauna nodul cel mai usor din multimea (VS), pentru a fi inserat in multimea S se poate spune ca el utilizeaza o strategie de tip GREEDY. S-a aratat insa ca metoda GREEDY nu conduce intotdeauna la rezultate optimale, dar urmatoarea teorema si corolarul ei arata ca algoritmul DIJKSTRA calculeaza intr-adevar drumurile cele mai scurte.
Cheia pentru a arata acest lucru este ca de fiecare data cand nodul u este inserat in S avem de fapt d(u)=DEL(s,u).
Teorema (de corectitudine a algoritmului DIJKSTRA)
Daca se executa algoritmul lui DIJKSTRA pe un graf orientat, ponderat G=(V, E) cu o functie de ponderare W:E R+ si un nod sursa sIV atunci la terminare d(u)=DEL(s,u) oricare ar fi uIV.
Demonstratie
Se va arata ca pentru fiecare nod uIV avem relatia d(u)=DEL(s,u), atunci cand nodul u este inserat in multimea S si se arata ca aceasta egalitate se mentine si dupa inserare.
Pentru demonstratia aceasta se foloseste metoda reducerii la absurd. Fie u primul nod pentru care d(u)¹DEL(s,u) atunci cand el este inserat in multimea S. Se va focaliza atentia asupra situatiei existente la inceputul iteratiei buclei while, cand nodul u este inserat in multimea S, pentru a se obtine o contradictie. La acest moment de timp se examineaza cel mai scurt drum dintre nodul s si nodul u. Trebuie sa avem s¹u deoarece s este primul nod inserat in S si d(u)=DEL(s,s)=0 la acest moment de timp.
Deoarece u¹s, rezulta ca S¹Æ exact inainte ca nodul u sa fie inserat in S, deci trebuie sa existe un drum de la nodul s la nodul u astfel incat d(u)=DEL(s,u)=¥ care conform Corolarului anterior ar viola presupunerea ca d(u)¹DEL(s,u). Deoarece exista cel putin un drum, exista un drum cel mai scurt de la nodul s la nodul u si fie acesta drumul p. Deci drumul p conecteaza un nod din multimea S, fie acesta s, la un nod din (VS), fie acesta u.
Se considera primul nod y de pe drumul p astfel incat yI(V-S) si fie xIV predecesorul lui y.
Dupa cum se va arata in urmatoarea figura drumul p poate fi descompus in doua subdrumuri p1 si p2 astfel:
![]()
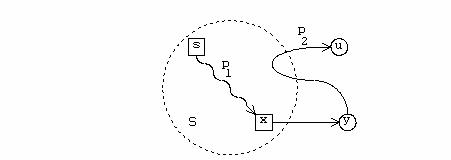
In aceasta figura nodul y este primul nod de pe drumul ce nu este in multimea (VS) si xIS este predecesorul lui y, (x si y sunt distincte, dar putem avea x=s sau y=u).
Drumul p2 poate sa intre sau nu in multimea S.
Se afirma ca d(y)=DEL(s,y) cand nodul u este inserat in multimea S. Pentru a demonstra aceasta afirmatie se observa ca xIS, atunci deoarece nodul u este ales ca primul nod pentru care avem d(u)¹DEL(s,u) cand el este inserat in multimea S. Am avut d(x)=DEL(s,x) cand nodul x a fost inserat in multimea S. Muchia (x, y) a fost relaxata la acel moment de timp astfel incat se poate scrie conform Lemelor anterioare, relatia: d(y)=DEL(s,y).
Deoarece nodul y apare inaintea lui u pe cel mai scurt drum de la nodul s la nodul u, toate ponderile muchiilor sunt pozitive si avem: DEL(s,y)£DEL(s,u) si astfel avem: d(y)=DEL(s,y)£DEL(s,u)£d(u). (din Leme)
Deoarece nodurile u si y se afla in multimea (VS), cand nodul u a fost deja ales (a cincea linie a algoritmului DIJKSTRA) avem: d(u)£d(y).
Din ultimele inegalitati rezulta faptul ca: d(y)=DEL(s,y)=DEL(s,u)=d(u) ceea ce contrazice alegerea nodului u. Rezulta ca la un moment de timp in care nodul uIV este inserat in multimea S, avem: d(u)=DEL(s,u) si din Lemele anterioare, aceasta egalitate se pastreaza si dupa aplicarea algoritmului.
Corolar
Daca se executa algoritmul lui DIJKSTRA pe un graf orientat ponderat G=(V, E) care are o functie de ponderare W nonnegativa si un nod sursa s, atunci la terminare, subgraful predecesor Gp este arborele celor mai scurte drumuri cu radacina s.
Demonstratie
Rezulta imediat din Teorema si din Lema anterioara.
Se poate rezolva acum problema: - cat de rapid este algoritmul lui DIJKSTRA?
Se considera intai cazul in care se intretine o coada de prioritati Q=VS implementata ca un masiv. Pentru o astfel de implementare, fiecare operatie EXTRACT-MIN consuma un timp O(|V|) si existand cardinal de V de astfel operatii rezulta ca timpul total pentru executia lui EXTRACT-MIN este de ordinul O(|V|2). Fiecare nod vIV este inserat in multimea S exact o data, astfel incat fiecare muchie din lista de adiacenta ADJ(v) este examinata in bucla FOR exact o data, in timpul algoritmului. Deoarece numarul total de muchii din toate listele de adiacenta este egal cu |E| rezulta ca numarul total de iteratii este |E| pentru bucla FOR (fiecare iteratie consumand un timp O(1)).
Deci timpul de executie al intregului algoritm este O(|V|2+|E|)=O(|V|2).
Observatie
Din cele discutate (vezi operatia EXTRACT-MIN) rezulta ca este util sa se implementeze cozile de prioritate cu ajutorul movilelor binare.
Algoritmul rezultat se numeste Algoritmul lui DIJKSTRA modificat si rezulta ca fiecare operatie EXTRACT-MIN consuma un timp de ordinul O(log|V|).
Ca si inainte exista |V| astfel de operatii, iar timpul de construire a unei movile binare este de ordinul O(|V|). Operatia de asignare d(v) d(u)+W(u,v) din functia de relaxare (RELAX) este realizata prin apelul DECREMENTARE- CHEIE(Q,v, d(u)+W(u,v)) care consuma un timp de ordinul O(log|V|) si exista cel mult |V| astfel de operatii.
Deci timpul total de executie este O((|V|+|E|).log|V|) adica, O(|E| log|V|). Acest lucru este valabil daca toate nodurile pot fi atinse din nodul sursa.
Se poate considera de fapt ca timpul pentru un astfel de algoritm este O(|V|log|V|+|E|) in cazul implementarii cozii de prioritati Q cu ajutorul movilelor FIBONACCI. Timpul de amortizare pentru fiecare din cele |V| operatii EXTRACT-MIN este O(log|V|) si fiecare din cele |E| apeluri DECREMENTARE-CHEIE consuma numai O(1) timp.
Din punct de vedere istoric movilele FIBONACCI au fost motivate de observatia ca in Algoritmul lui DIJKSTRA modificat exista mai multe apeluri potentiale pentru DECREMENTARE-CHEIE decat pentru EXTRACT-MIN, astfel incat orice metoda de reducere a timpului de executie pentru operatia DECREMENTARE-CHEIE la O(log|V|), fara cresterea timpului de executie a operatiei EXTRACT-MIN, ar conduce la o implementare asimptotic mai rapida.
Observatie
Algoritmul DIJKSTRA prezinta anumite similaritati atat cu algoritmul de parcurgere in latime cat si cu algoritmul lui PRIM care calculeaza arborele de acoperire minima.
Legatura cu algoritmul de parcurgere in latime este facuta prin multimea S care corespunde multimii de noduri negre din algoritmul BREADTH FIRST SEARCH, astfel incat nodurile din multimea S au ponderile drumului final cel mai scurt, iar nodurile negre au atasate distantele corecte date de algoritmul BREADTH FIRST SEARCH.
Legatura cu algoritmul lui PRIM este data de folosirea cozii de prioritate pentru obtinerea nodurilor usoare care se afla in afara multimii date (multimea S din algoritmul lui DIJKSTRA si arborele care se obtine in algoritmul lui PRIM), apoi se insereaza nodul cel mai usor in multime si se actualizeaza ponderile nodurilor care raman in afara multimii.
In continuare se prezinta implementarea in limbajul C a algoritmului Dijkstra:
#include <stdio.h>
#include <values.h>
#include <alloc.h>
#define MAX_NOD 10
/* graful este reprezentat prin liste de adiacenta si urmatoarele structuri implementeaza acest lucru */
typedef struct n *pnod, tnod;
typedef struct x graf_type[MAX_NOD];
graf_type G;
int w[MAX_NOD][MAX_NOD], nr_nod, PI[MAX_NOD], d[MAX_NOD], s;
void RELAX(int u,
int v,
int w[MAX_NOD][MAX_NOD],
int d[MAX_NOD])
return;
void INITIALIZARE_SINGURA_SURSA(int nr_nod,
int s,
int d[MAX_NOD],
int PI[MAX_NOD])
d[s]=0;
return;
void DIJKSTRA(graf_type G,
int w[MAX_NOD][MAX_NOD],
int nr_nod,
int s,
int PI[MAX_NOD],
int d[MAX_NOD])
nr_Q=nr_nod;
Q[0]=s;
Q[s]=0;
REFQ[s]=0;
REFQ[0]=s;
while(nr_Q)
S[nr_S++]=u;
for(p=G[u].ADJ; p ; p=p->next)
}
}
}
return;
void citeste_graf(graf_type G, int *nr_nod, int w[MAX_NOD] [MAX_NOD], int *s)
else
G[i].ADJ=p;
}
printf('Introduceti nodul sursa:');
scanf('%d', s);
int main()
Algoritmul lui BELLMAN-FORD rezolva problema drumurilor cele mai scurte cu o singura sursa in cazul cel mai general in care ponderile muchiilor pot fi si negative.
Se considera un graf dat G=(V, E) orientat, ponderat si se considera un nod sursa s precum si o functie de ponderare W:E R. Algoritmul BELLMAN-FORD returneaza o valoare booleana care va indica faptul ca exista sau nu exista in graf un ciclu cu pondere negativa care poate fi atins din nodul sursa. Daca exista un astfel de ciclu, algoritmul arata ca problema data nu are solutie. Daca nu exista un astfel de ciclu, algoritmul furnizeaza drumurile cele mai scurte si ponderile lor.
Ca si in algoritmul lui DIJKSTRA, algoritmul BELLMAN-FORD utilizeaza tehnica relaxarii pentru a creste in mod progresiv valoarea estimata d(v) a ponderii unui nod aflat pe drumul cel mai scurt de la nodul sursa s la nodul vIV pana cand se obtine ponderea celui mai scurt drum, notata cu DEL(s,v). Algoritmul returneaza valoarea TRUE daca si numai daca graful nu contine cicluri cu pondere negativa care sa fie atinse din nodul sursa.

Dupa executarea initializarilor uzuale, algoritmul executa un numar de (|V|-1) treceri prin muchiile grafului. Fiecare trecere este o iteratie a primei bucle FOR si consta in relaxarea fiecarei muchii a grafului exact o data. Dupa cele (|V|-1) treceri, ultima bucla FOR verifica existenta ciclului cu pondere negativa si returneaza o valoare booleana adecvata.
Algoritmul BELLMAN-FORD se executa intr-un timp O(|V|. |E|) deoarece initializarea din prima linie consuma un timp O(|V|), iar fiecare din cele (|V|-1) treceri referitoare la muchiile grafului si executate de prima bucla FOR, consuma un timp O(|V|), iar ultima bucla FOR consuma un timp O(|E|). Fiind instructiuni secventiale rezulta ca timpul total de executie al algoritmului este O(|V|.|E|).
Exemplu
Executia algoritmului BELLMAN-FORD va fi prezentata in urmatoarele figuri[10], si se considera drept nod sursa nodul z, valoarea d este aratata in interiorul fiecarui nod, iar muchiile dublate indica valorile PI. In cazul particular al exemplului, fiecare trecere realizeaza relaxarea muchiilor in ordine lexicografica, adica in ordinea: (u,v); (u,x); (u,y); (v,u); (x,v); (x,y); (y,v); (y,z); (z,u); (z,x).
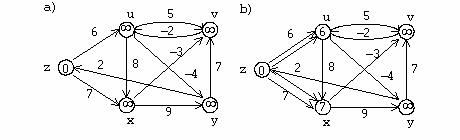
Figura a) prezinta situatia exact inaintea primei treceri executate asupra muchiilor grafului, iar urmatoarele figuri arata transformarile grafului datorita algoritmului BELLMAN-FORD.
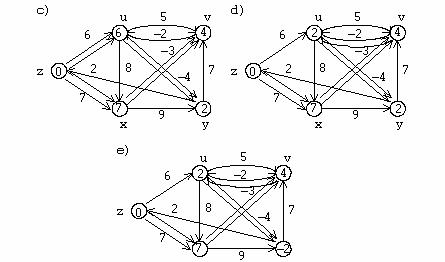
Figura e) arata valoarea 'd' si PI pentru cazul final. Pentru acest exemplu algoritmul BELLMAN-FORD va intoarce valoarea TRUE.
Demonstrarea corectitudinii pentru algoritmul BELLMAN-FORD porneste cu aratarea faptului ca nu exista cicluri cu pondere negativa si ca se calculeaza corect ponderile drumurilor cele mai scurte pentru toate nodurile care pot fi atinse din nodul sursa. Pentru aceasta se va obtine urmatorul rezultat intermediar.
Lema
Se considera dat un graf G=(V, E) orientat, ponderat, cu un nod sursa s si o functie de ponderare W:E R si se presupune ca graful G nu contine cicluri cu pondere negativa care sa fie atinse din nodul sursa s.
Atunci la terminarea algoritmului BELLMAN-FORD se obtine d(v)=DEL(s,v) pentru toate nodurile v care pot fi atinse din nodul sursa s.
Demonstratie
Fie v un nod care poate fi atins din nodul sursa s si fie p=<v0, v1, , vk> drumul cel mai scurt de la nodul v la nodul s unde v0=s si vk=v. Se presupune ca p este un drum simplu astfel incat k£(|V|-1). Se va demonstra prin inductie dupa i= 0, 1, , k ca vom avea d(vi)=DEL(s,vi) dupa cea de a i-a trecere asupra muchiilor din graful G si in plus aceasta egalitate se pastreaza si dupa aceasta trecere. Deoarece exista (|V|-1) astfel de treceri rezulta ca afirmatia este suficienata pentru a demonstra lema.
Pentru inceput d(v0)=DEL(s,v0)=0 si dupa initializare, conform Lemelor anterioare aceasta egalitate se pastreaza. Conform inductiei vom avea d(vi-1)=DEL(s,vi-1) dupa cea de-a (i-1)-a trecere. Muchia (vi-1,vi) este relaxata in cea de a i-a trecere si conform Lemelor anterioare rezulta ca d(vi)=DEL(s,vi) dupa cea de a i-a trecere.
Corolar
Se considera dat un graf G=(V, E) orientat, ponderat, cu un nod sursa s si o functie de ponderare W:E R si se presupune ca graful G nu contine cicluri cu pondere negativa care sa fie atinse din nodul sursa s.
Atunci pentru fiecare nod vIV, exista un drum de la nodul s la nodul v daca si numai daca procedura BELLMAN-FORD se termina cu d(v)<¥ cand se ruleaza pentru graful G.
Demonstratie
Demonstratia este similara cu cea de la Lema anterioare si este lasata ca exercitiu.
Teorema (de corectitudine a algoritmului BELLMAN-FORD)
Se considera ca procedura BELLMAN-FORD se executa asupra unui graf G=(V, E) orientat, ponderat, cu un nod sursa s si o functie de ponderare W:E R. Daca graful G nu contine cicluri cu pondere negativa care sa fie atinse din nodul sursa s, atunci algoritmul furnizeaza valoarea TRUE si d(v)=DEL(s,v) pentru orice nod vIV iar subgraful predecesor Gp contine arborele celor mai scurte drumuri cu radacina s.
Daca graful G contine un ciclu cu pondere negativa care poate fi atins din nodul sursa s, atunci procedura returneaza valoarea FALSE.
Demonstratie
Se presupune ca graful G nu contine cicluri cu pondere negativa care sa fie atinse din nodul sursa s. Se demonstreaza mai intai afirmatia ca la terminare d(v)=DEL(s,v) pentru orice nod vIV. Daca nodul v poate fi atins din nodul sursa s, Lema anterioara demonstreaza aceasta afirmatie.
Daca v nu poate fi atins din nodul sursa s, afirmatia rezulta din Corolar. Deci aceasta egalitate este demonstrata.
Lemele anterioare impreuna cu afirmatia de mai sus conduc la afirmarea faptului ca subgraful Gp este arborele drumurilor cele mai scurte.
In continuare dorim sa aratam ca procedura BELLMAN-FORD returneaza valoarea TRUE.
La terminare pentru toate muchiile (u,v) IE avem:
d(v)=DEL(s,v) £(Lema)£DEL(s,u)+W(u,v)=d(u)+W(u,v).
Din acest motiv nici unul din testele din instructiunea IF nu conduce la returnarea valorii FALSE si deci se obtine returnarea valorii TRUE.
Se presupune acum ca graful G contine un ciclu de pondere negativa notat c=<v0, v1, , vk> unde v0=vk care poate fi atins din nodul sursa s.
Avem:
![]()
Se presupune prin reducere la absurd ca algoritmul BELLMAN-FORD returneaza valoarea TRUE. Rezulta d(vi)£d(vi-1)+W(vi-1 ,vi) pentru iI(1,k). In aceasta inegalitate se face insumarea de-a lungul ciclului c de mai sus si se obtine:
![]()
Dar asa cum s-a aratat in Lemele anterioare, fiecare nod din ciclul c apare exact o data in fiecare din cele doua sume, astfel incat avem:
![]()
In plus, conform Corolarului, d(vi) este finit pentru orice iI(1,k). Din toate acestea rezulta:
![]()
lucru care contrazice faptul ca ponderea ciclului este negativa.
Rezulta ca algoritmul BELLMAN-FORD returneaza valoarea TRUE daca graful G nu contine cicluri de pondere negativa care sa fie atinse din nodul sursa s si returneaza valoarea FALSE in caz contrar.
In continuare se prezinta implementarea algoritmului BELLMAN-FORD:
#include <stdio.h>
#include <values.h>
#include <>alloc.h
#define MAX_NOD 10
#define FALSE 0
#define TRUE 1
typedef struct n *pnod, tnod;
typedef struct x graf_type[MAX_NOD];
graf_type G;
int w[MAX_NOD][MAX_NOD], nr_nod, PI[MAX_NOD], d[MAX_NOD], s;
void RELAX(int u,
int v,
int w[MAX_NOD][MAX_NOD],
int d[MAX_NOD])
return;
void INITIALIZARE_SINGURA_SURSA(int nr_nod,
int s,
int d[MAX_NOD],
int PI[MAX_NOD])
d[s]=0;
return;
int BELLMAN_FORD(graf_type G,
int w[MAX_NOD][MAX_NOD],
int nr_nod,
int s,
int PI[MAX_NOD],
int d[MAX_NOD])
}
for(j=0; j < nr_nod; j++)
for(p=G[j].ADJ; p; p=p->next)
return(TRUE);
void citeste_graf(graf_type G, int *nr_nod, int w[MAX_NOD][MAX_NOD], int *s)
else
G[i].ADJ=p;
}
printf('Introduceti nodul sursa:');
scanf('%d', s);
int main()
else
printf('Nu se poaten');
return(0);
Probleme propuse
1. Se considera o retea de calculatoare. Conexiunile directe dintre calculatoare sunt reprezentate cu ajutorul unui graf orientat si se cunoaste lungimea fiecarei asfel de conexiuni. Se presupune ca un calculator trimite un mesaj catre celelalte calculatoare din cadrul retelei.
Se cere determinarea lungimii drumului minim pentru acele calculatoare care primesc acest mesaj (Dijkstra).
2. Un joc pe calculator presupune plimbarea unui robot pe strazile unui oras virtual. Daca robotul se plimba pe anumite strazi, el se incarca cu o energie pozitiva egala cu ponderea atasata acelei strazi. Daca insa, robotul se plimba pe alte strazi ale orasului, atunci el pierde energie (se incarca 'negativ') egala cu ponderea atasata strazii respective. La un moment dat se stie graful atasat unui posibil parcurs pentru robot si nodul de plecare. Se presupune ca energia initiala a robotului este suficient de mare astfel incit el sa poata ajunge, plecind din nodul initial, in oricare dintre celelalte noduri ale grafului (robotul nu-si poate continua drumul dintr-un nod in care a ajuns, daca este incarcat cu energie negativa).
Se cere determinarea lungimilor drumurilor cele mai scurte si a ponderilor lor, de la nodul initial la fiecare dintre celelalte noduri ale grafului dat (Bellman-Ford).
Intr-un depozit de marfuri exista un robot care aduce materialele comandate la un moment dat. Materialelel sunt depozitate in niste cutii aflate in anumite puncte din depozit. Se cunosc toate legaturile directe dintre perechile de cutii din cadrul magaziei precum si lungimile lor. Robotul se poate deplasa numai de-a lungul acestor legaturi. Robotul se afla intr-o pozitie initiala S. Se cunoaste de asemenea, daca exista legaturi directe intre pozitia S si celelalte pozitii din magazie unde se afla depozitate marfuri si in caz afirmativ, lungimile acestor legaturi.
Se cere determinarea celor mai scurte drumuri si a lungimilor lor, de la pozitia initiala a robotului pina la fiecare dintre cutiile cu materiale (Dijkstra).
4. Pentru plata impozitelor, un cetatean trebuie sa mearga la N ghisee aflate la parterul unei cladiri. Intre anumite ghise se afla coridoare de acces direct avind anumite lungimi. Se cunosc de asemenea legaturile directe prin coridoare intre punctul de intrare in cladire si diversele ghisee, impreuna cu lungimile lor.
Se cere determinarea celor mai scurte drumuri de la intrarea in cladire pina la fiecare dintre cele N ghisee (Dijkstra).
5. Se considera problema 4, dar robotul se poate plimba de-a lungul unor legaturi si se incarca cu energie pozitiva si poate pierde energie daca se plimba pe alte legaturi.
Se cere determinarea lungimilor drumurilor cele mai scurte si a ponderilor lor, de la nodul initial la fiecare dintre celelalte noduri ale grafului dat (Bellman-Ford).
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 5717
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved