TRANSMISII IN BANDA DE BAZA

In TD in banda de baza, datele sunt emise sub forma unor impulsuri de curent continuu. Secventele de date sunt constituite din elemente de semnal, care se deosebesc de celelalte prin amplitudine, durata sau pozitie relativa. ELEMENTUL DE SEMNAL, cunoscut si sub denumirile de SEMNAL ELEMENTAR, IMPULS ELEMENTAR sau SEMNAL UNITAR este si cea mai scurta parte componenta a codului considerat, care reprezinta modul de asociere dintre date si forma folosita pentru transmisie.

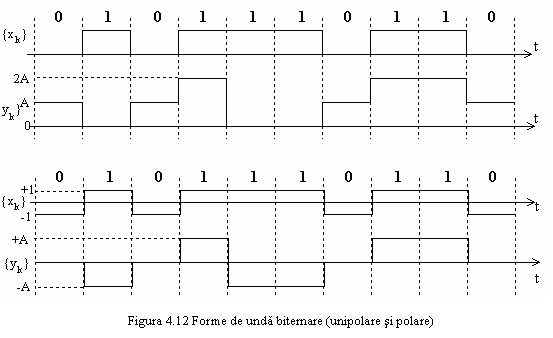
Cel mai simplu cod - codul NRZ (Non-Return to Zero) este compus din elemente binare de semnal, de aceeasi durata T, de forma reprezentata in figura 4.1a.

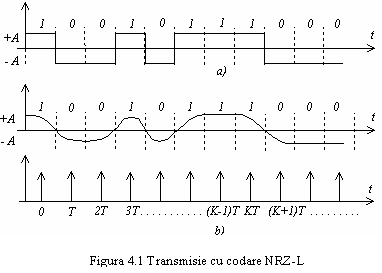Aceasta forma de unda poate fi caracterizata ca fiind un semnal binar antipodal in banda de baza. Semnalul este antipodal deoarece bitul 1 fiind reprezentat prin nivelul +A, iar bitul 0 prin -A, ele satisfac:

(4.1)

unde si sunt formele de unda folosite pentru transmisia unui bit 1 si respectiv unui bit 0.

Semnalul este in banda de baza deoarece spectrul sau se intinde pana la frecventa 0 Hz (curent continuu) sau frecvente foarte joase si transporta informatia prin intermediul valorilor avute in anumite puncte , k = 0, 1, 2,....

Prin modificarea formei semnalului asa cum se arata in figura 4.1b, tranzitiile abrupte au fost eliminate, astfel incat din spectrul semnalului au fost eliminate sau reduse in mare masura frecventele inalte. Forma de unda cu flancurile rotunjite, avand un aspect mai ingust, realizeaza o transmisie mai eficienta, informatia transportata poate fi recuperata prin sondarea formei de unda la momentele kT. Partile de joasa frecventa ale celor doua spectre sunt in esenta identice, acestea fiind determinate nu de flancurile formei de unda, ci de paliere.

In majoritatea sistemelor de comunicatii, largimea benzii transmise se afla intr-o stransa interdependenta cu pretul de cost, ceea ce impune limitarea benzii semnalului. In plus, limitarea benzii transmise la portiunea unde energia semnalului este maxima minimizeaza zgomotele si interferentele suparatoare. Impulsurile rectangulare, cu un continut spectral foarte bogat si extins la frecvente inalte, nu sunt indicate pentru TD.

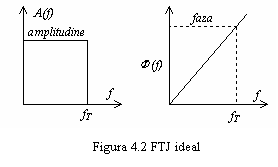Se pune asadar problema de a sti in ce masura putem limita spectrul semnalului, fara a afecta performantele TD. In acest scop se pleaca de la un FTJ ideal, cu caracteristicile de amplitudine si faza reprezentate in figura 4.2.

Se observa ca

(4.2)

iar defazajul creste liniar cu frecventa.

Semnalul la iesirea FTJ este dat de integrala Fourier:

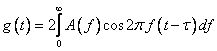(4.3)

unde este intarzierea de transmisie introdusa de filtru.

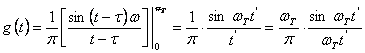(4.4)

unde .

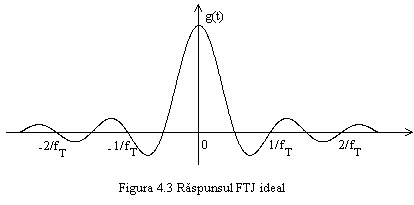Se observa din ecuatia (4.4) ca, plecand de la o functie cu densitate spectrala constanta intr-o banda de frecventa limitata, am obtinut in domeniul timp un raspuns de forma , reprezentat in figura 4.3.

Raspunsul prezinta zerouri la momentele: .

Deci, se pot transmite impulsuri fara interferenta intersimboluri la momentele , situatie ilustrata in figura 4.4 printr-o secventa de date 110010000. Valoarea , denumita interval Nyquist, corespunde unei transmisii cu viteza egala cu dublul frecventei de taiere a FTJ.

FTJ considerat ideal nu este realizabil practic, iar raspunsul tip nu este indicat, deoarece odata cu aparitia unei mici erori de sincronizare in localizarea momentelor de sondare a semnalului, erorile introduse descresc in timp sub forma , ceea ce corespunde unei serii de forma , care nu este convergenta. Aceasta inseamna ca portiunile laterale ale impulsurilor (cozile) se pot aduna si introduce dificultati in interpretarea valorii binare a impulsului, adica IIS.

Acest lucru poate fi observat in figura 4.4. Esantionarea la momente diferite de cele ideale face ca in loc de 3 esantioane egale cu 1 si restul egale cu zero sa avem mai multe esantioane diferite de zero, adica interferenta intersimboluri.

Momentele de esantionare sunt diferite de cele ideale intrucat ele sunt generate de un circuit de sincronizare care extrage informatia de tact din semnalul receptionat care este distorsionat si insotit de zgomot. Aceasta introduce jitter de faza modulatie parazita de faza), momentele de esantionare reale fiind distribuite in jurul celor ideale.

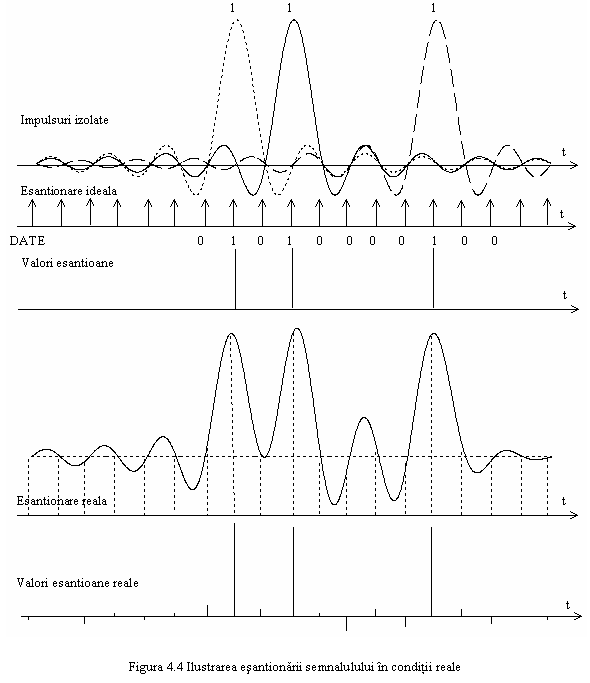
Avand in vedere irealizabilitatea fizica a raspunsului de tip sinc (implica intarziere infinita) vom cauta un semnal cu urmatoarele proprietati:

sa fie produs de un filtru realizabil fizic, cu atenuare lina;

sa fie robust la erori de sincronizare (esantionare langa momentele ideale);

sa pastreze zerourile raspunsului de tip sinc.

1 Criteriul I NYQUIST

In transmisia semnalelor de banda limitata, Nyquist a adus contributii foarte importante referitoare la suprimarea IIS. El demonstreaza ca in locul FTJ ideal, irealizabil fizic, se poate folosi orice FTJ cu panta simetrica de cadere a caracteristicii in jurul frecventei de taiere , astfel pastrandu-se zerourile de la momentele de esantionare.

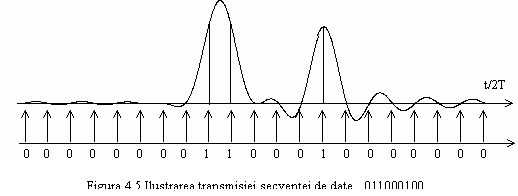
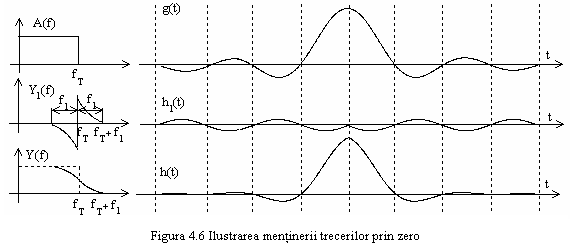
Pentru aceasta, la FTJ ideal se adauga o functie de transmitanta cu valori reale , asa cum se arata in figura 4.6, care prezinta simetrie impara de tipul:

(4.5)

obtinandu-se un filtru cu caracteristicile de transmitanta:

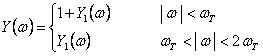(4.6)

Deplasand originea timpului in , raspunsul devine:

(4.7)

cu

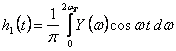
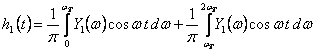(4.8)

In prima integrala din (4.8) substituim:

(4.9)

iar in a doua integrala:

(4.10)

Obtinem:

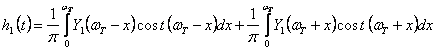
(4.11)

si conform (4.5):

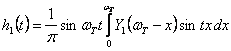(4.12)

Factorul ne arata ca pentru , deci s-au pastrat zerourile de la momentele de esantionare, asa cum se observa si din figura 4.6.

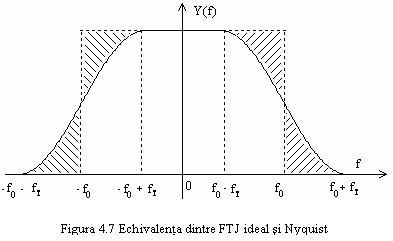
In figura 4.7 se prezinta echivalenta dintre FTJ ideal si FTJ cu panta de cadere simetrica in jurul frecventei de taiere . Portiunile hasurate se compenseaza reciproc.

Primul criteriu al lui Nyquist poate specifica in domeniul frecventa si conditiile de IIS nula. Aceasta este nula numai daca raspunsul are zerouri in toate momentele de sondare, , cu exceptia momentului propriu (k = 0), unde .

In sistemele practice de TD, pentru transmisia cu viteza se foloseste o banda ceva mai mare decat cea teoretic necesara , de obicei cuprinsa intre si . Excesul de banda este necesar pentru a putea realiza fizic FTJ formator. Cel mai des se utilizeaza un filtru care produce la iesirea sa un spectru de tipul cosinus ridicat (figura 4.8a), compus dintr-o portiune plata si o portiune cu cadere sinusoidala. Notand excesul de banda cu r (), putem defini caracteristica de frecventa a filtrului ca:

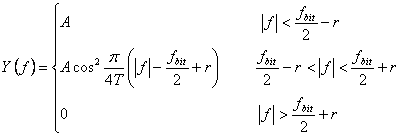(4.13)

Forma de unda a impulsului obtinut la iesirea filtrului cu caracteristica este data de:

(4.14)

si este reprezentata in figura 4.8b.

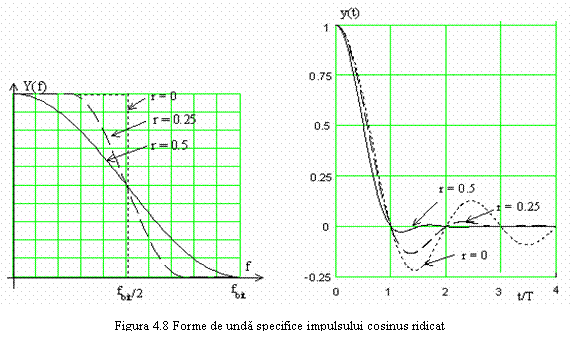
Remarcam urmatoarele:

1. Latimea de banda necesara este ; valoarea minima este iar cea maxima ,

2. Cu cresterea lui r, creste banda ocupata, dar trena impulsului se amortizeaza mai repede, ceea ce reduce IIS si cerintele impuse circuitului de sincronizare,

3. Cazul conduce la un spectru cosinusoida ridicata clasic, cu proprietati avantajoase si pentru sincronizare,

4. Spectrul se bucura de proprietatea ca este real, non-negativ iar .

2 Criteriul II Nyquist

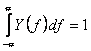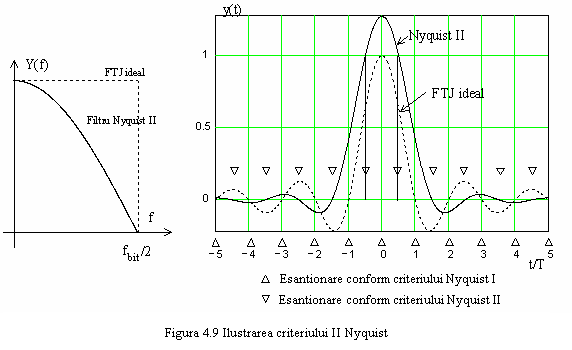
Criteriul II al lui Nyquist se refera la introducerea deliberata de interferenta intersimboluri intr-o masura limitata (la doua momente de esantionare succesive) si recuperarea informatiei prin esantionarea semnalului la momente de timp decalate cu T/2 fata de cele din criteriul Nyquist I.

Esantionarea are deci loc nu in centrele impulsurilor ci la jumatatea intervalelor dintre 2 simboluri succesive, asa cum se observa din figura 4.9.

Fata de FTJ ideal, criteriul II Nyquist utilizeaza un filtru mai restrictiv, care va produce o alungire in domeniul timp al lobului principal al impulsului, astfel ca forma de unda utilizata pentru transmisie are doua esantioane diferite de zero. Se considera filtrul FTJ definit de:

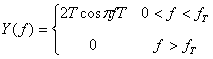(4.15)

unde este frecventa de taiere a FTJ ideal. Ne reamintim ca daca se poate face transmisie cu viteza .

Raspunsul la impuls al filtrului este

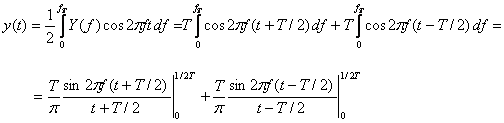(4.16)

(4.17)

In figura 4.9 este reprezentata caracteristica de transfer a filtrului trece jos si raspunsul sau y(t). Raspunsul y(t) prezinta zerouri pentru multiplii impari pozitivi sau negativi ai lui T/2, cu exceptia lui

(4.18)

Putem scrie conditia pe care o satisface forma de unda definita de criteriul II Nyquist:

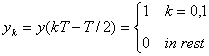(4.19)

sau decaland cu T/2 originea timpului, avem

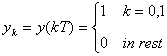(4.20)

Spre deosebire de acesta, criteriul I Nyquist specifica

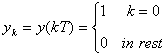(4.21)

Se observa din rel.(4.18) ca valoarea esantionului va depinde atat de bitul transmis la momentul k, cat si de cel transmis la momentul anterior . Deci, daca consideram transmisia ideala, IIS provine numai de la simbolul precedent. Considerand o transmisie binara dublu curent, cu simbolurile de date , valorile esantionului (media valorilor simbolurilor alaturate) vor fi , corespunzator situatiilor , , si respectiv si . Este uzual, ca impartind la 2 valorile esantioanelor sa consideram ca care sunt valorile ternare clasice.

Raspunsul y(t), pe baza rel.(4.16) mai poate fi scris ca:

(4.22)

adica suma a doua raspunsuri de tip corespunzatoare FTJ ideal sau conform criteriului I al lui Nyquist, decalate cu T intre ele. Cele doua componente si semnalul rezultant sunt ilustrate in figura 4.10.

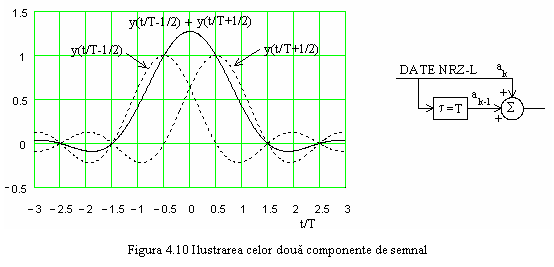
Semnalul rezultat are o trena mai rapid descrescatoare datorita relatiei de antifaza dintre trenele celor doua impulsuri de tip , decalate intre ele cu T. Se observa ca IIS va fi mai mica, avand in vedere viteza sporita de scadere a valorii esantioanelor, in cazul esantionarii in conditii reale, cu eroare de sincronizare si zgomot prezent in canal. Acest semnal este produs de circuitul reprezentat in figura 4.10. Functia sa de transfer este

(4.23)

(4.24)

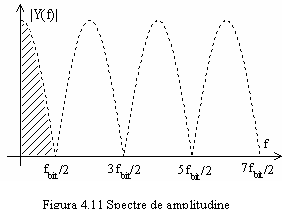Acesta din urma reprezinta spectrul de amplitudine al semnalelor la iesirea din filtru si este reprezentat in figura 4.11. Se observa ca este asemanator cu cel dat de rel.(4.15), exceptand caracterul sau periodic.

Efectele acestei operatii, cunoscuta sub denumirea de codare biternara sunt urmatoarele:

- deplasarea si concentrarea energiei semnalului in banda ;

- crearea de nuluri spectrale la frecventa si multiplii impari ai acesteia;

- extinderea duratei lobului principal al impulsului de la 2T la 3T si introducerea de IIS in mod controlat, astfel ca valoarea esantionului va depinde atat de bitul transmis la momentul kT, cat si de cel transmis la momentul anterior .

- reducerea IIS prin cresterea vitezei de scadere in timp a trenei impulsului.

Circuitul reprezentat in figura 4.10 este cunoscut sub denumirea de codor biternar, semnalul de iesire fiind un semnal ternar. Metoda de transmisie bazata pe filtrul cu caracteristica , data de rel. (4.15) si raspuns la impuls descris de (4.17), se numeste biternara.

Considerand doua simboluri de date succesive si , semnalul codat biternar este

(4.25)

de unde (4.26)

Recuperarea informatiei de date la receptie se face pe baza valorii esantionului din forma de unda pseudoternara transmisa si a simbolului de date precedent . Forma de unda este pseudoternara intrucat simbolurile ternare sunt asociate in mod determinist cu cele binare.

Putem remarca din figura 4.10 faptul ca daca simbolul este afectat de eroare, atunci va fi si el afectat, iar eroarea se propaga. Pentru a elimina propagarea erorii sa consideram urmatoarele chestiuni legate de codarea biternara:

- o secventa lunga de biti 1 va fi reprezentata de nivelul +,

- o secventa lunga de biti 0 va fi reprezentata prin nivelul ,

- o secventa lunga de biti alternanti 01 va fi reprezentata prin nivelul 0.

Evident, primul bit din secventa lunga de biti 1 sau 0 va fi reprezentat de nivelul 0, deoarece vine dupa un bit de valoare opusa, iar bitii urmatori vor fi codati prin nivelul +, respectiv . Atunci, se poate elimina propagarea erorii prin folosirea unei precodari la emisie, astfel incat sa avem asociate nivelele + si cu un bit, de exemplu cu bitul 1, iar nivelul ternar, cu celalalt bit, de exemplu 0.

Recuperarea informatiei se poate face prin redresarea dubla alternanta a semnalului ternar (nivelele + si trec in + iar nivelul ternar 0 in 0, urmat o decizie binara, cu un comparator cu pragul reglat adecvat. Prin precodare secventa de date de intrare este transformata intr-o secventa ce satisface relatia:

(4.27)

unde - semnifica sumare modulo-2 (SAU EXCLUSIV). Atunci,

(4.28)

iar (4.29)

sau

(4.30)

Deci,

implica si , iar

implica iar .

unde sunt nivelele ternare extreme.

In acest fel se simplifica decodarea, deoarece prin redresarea secventei ternare obtinem o forma de unda binara, in care nivelele vor corespunde cu bitul 1, iar nivelul 0 cu bitul 0.

3 Criteriul III Nyquist

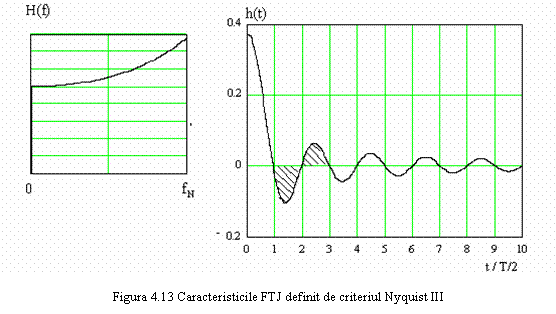
Criteriul al treilea dat de Nyquist utilizeaza un filtru trece jos avand caracteristica de frecventa reprezentata in figura 4.13 pentru frecventele pozitive si definita de relatia

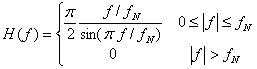(4.31)

Raspunsul sau la impuls h(t) este dat de

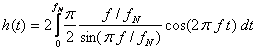(4.32)

si se bucura de proprietatea

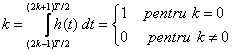(4.33)

adica integrala raspunsului la impuls intre momente de timp multipli impari de T/2, T fiind durata simbolului, este nula, cu exceptia intervalului propriu, centrat pe momentul 0.

Tinand cont de interpretarea geometrica a integralei, ce reprezinta suprafata subintinsa de curba, se observa din figura 4.13 ca suprafetele subintinse de lobii laterali ai raspunsului la impuls sunt egale, doua cate doua. Un exemplu se poate observa in figura 4.13, unde pentru claritate s-au reprezentat hasurat doua asemenea suprafete care se compenseaza reciproc.

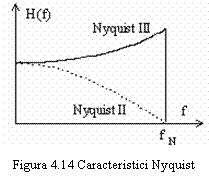
In figura 4.14 sunt reprezentate functiile de transfer ale FTJ definite de criteriile Nyquist II si III. Evident, caracteristica abrupta si discontinua a filtrului Nyquist III nu este realizabila fizic. Pentru realizarea practica se impune cresterea benzii sau scaderea vitezei de semnalizare sub viteza Nyquist, recurgand la solutia data de criteriul I Nyquist si realizand o caracteristicǎ ce aproximeazǎ pe cea idealǎ.

Criteriul III Nyquist ofera o metoda de recuperare a informatiei transmise bazata pe integrarea semnalului transmis pe durata unui symbol si luarea deciziei pe baza energiei semnalului receptionat. Aceasta tehnica de detectie este mai robusta, in special la zgomote de tip impulsiv, avand in vedere ca in general energia unui impuls de zgomot este mult mai mica decat cea a semnalului, dar in schimb amplitudinea lui este comparabila cu cea a semnalului. Esantionand semnalul insotit de zgomot la momentele de timp date de criteriile Nyquist I sau II, se poate intampla ca impulsul de zgomot sa apara uneori chiar la unele din aceste momente si sa mascheze semnalul, introducand erori.

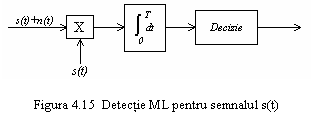
Circuitul folosit pentru detectie in acest caz, bazat pe integrarea semnaului, se numeste detector cu integrare si descarcare (integrate and dump) si reprezinta totodata si un detector de plauzibilitate maxima (ML maximum likelihood) in cazul utilizarii pentru semnalizare a impulsurilor rectangulare, ce au amplitudinea constanta in tot intervalul de semnalizare (0, T).

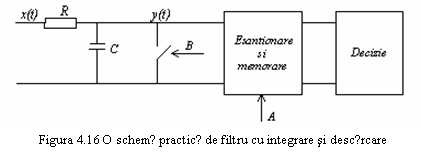
O schemǎ bloc de principiu a detectorului ML este reprezentatǎ in figura 4.15. O schemǎ practicǎ este reprezentatǎ in figura 4.16. Integratorul este realizat sub forma unui FTJ de tip RC, care pentru o constantǎ de timp τ mare in raport cu durata impulsului T, se comportǎ ca un integrator.

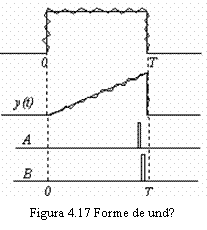
Formele de undǎ ce ilustreazǎ functionarea sa sunt prezentate in figura 4.17, pentru un impuls pozitiv si o singurǎ perioadǎ de integrare. Iesirea integratorului este cititǎ cu ajutorul impulsului A si memoratǎ de circuitul de esantionare si memorare.

Spre sfarsitul perioadei de integrare T, semnalul B este folosit pentru descǎrcarea condensatorului C (aducerea sarcinii la zero), pregǎtindu-l pentru o nouǎ integrare pe urmǎtorul interval de bit. Functionarea acestui detector este deci guvernatǎ de o bazǎ de timp sau circuit de sincronizare, care isi extrage informatiile de sincronizare din forma de undǎ receptionatǎ.

Intr-o transmisie realǎ, la intrarea in circuitul de esantionare si memorare se obtine o formǎ de undǎ compuse din rampe de tensiune de tipul celei din figura 4.17, cu polaritǎti pozitive sau negative, in functie de bitii transmisi (se presupune bitul 1 reprezentat prin nivelul +1, iar bitul 0 prin nivelul -1).

4 Semnale cu raspuns partial

Pentru a obtine un semnal cu spectru limitat la frecventa ideala Nyquist de 1/2T Hz se introduce IIS controlata in mai multe pozitii. Plecand de la raspunsul la impuls dat de primul criteriu al lui Nyquist, semnalele cu raspuns partial (SRP) au raspunsul la impuls de forma:

(4.34)

iar caracteristica de frecventa:

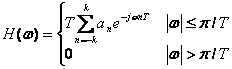(4.35)

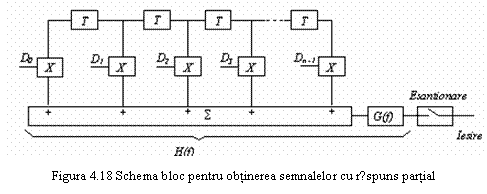
Relatia (4.35) este implementata cu ajutorul circuitului reprezentat in figura 4.18, cunoscut si sub denumirea de filtru binar transversal. Folosind pentru coeficientii de pondere a raspunsului tip diferite valori, se pot obtine proprietati utile pentru caracteristica de frecventa , cum ar fi:

Caracteristica H(f) sa fie continua si sa prezinte un numar de derivate continue si egale cu zero la

capetele intervalului de definitie.

Spectrul SRP sa prezinte un nul la frecventa 0 (c.c.) si la multiplii pari de

Spectrul SRP sa prezinte un nul la si la multiplii impari de

Continuitatea lui ) si a primelor sale k-1 derivate asigura amortizarea rapida a raspunsului la impuls h(t) dupa legea 1/, contribuind la reducerea energiei inmagazinate in trena lui h(t) si deci la reducerea IIS .

Spectrul nul la frecventa zero sau cu pondere redusa a componentelor de joasa frecventa pentru secventa de date este necesar pentru transmisiile pe linii metalice cu cuplaj prin transformator sau condensator, transmisiile BLU sau folosind frecvente pilot pentru reglajul automat al nivelului, sincronizare sau eliminarea fugii frecventei prin effect Doppler.

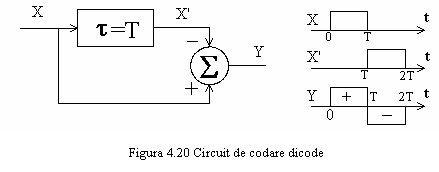
Fie coderul SRP din figura 4.18, care produce un semnal cu raspuns partial. Daca , coderul este cunoscut sub denumirea de dicode.Notand cu D operatorul de intarziere cu durata T, semnalul de la iesirea coderului dicode poate fi scris ca:

(4.36)

iar in general:

(4.37)

unde F(D) este functia de transfer a sistemului si are forma unui polinom in D, de gradul n,

(4.38)

(4.39)

corespund cu

(4.40)

Semnalele SRP pot fi produse de schema din figura 4.18, unde linia de intarziere compusa din celule cu intarzierea T poate fi implementata cu un registru de deplasare, daca semnalele implicate sunt binare.

Cele mai simple exemple de semnale cu raspuns partial sunt descrise de polinoamele de ordinul I si , care corespund semnalelor de tip dicode si respectiv biternar.

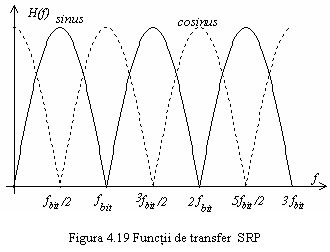
Caracteristica de frecventa pentru codul dicode este:

(4.41)

prezentand zerouri pentru sau unde este frecventa normalizata (), (vezi figura 4.19).

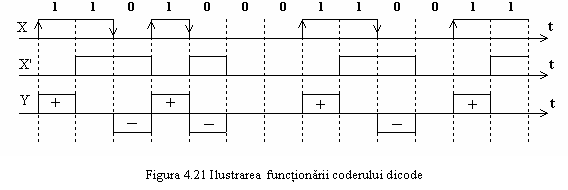
Coderul dicode este prezentat in figura 4.20. Se observa ca aplicand la intrarea sa un impuls de latime T, la iesire rezulta o forma de unda de latime 2T compusa dintr-un impuls pozitiv urmat de unul negat Mai remarcam ca pentru a vizualiza forma de unda de la iesire nu este suficient un singur interval de timp de latime T, pe acesta semnalul fiind observat partial. De aici si denumirea de semnale cu raspuns partial folosita pentru semnalele generate prin aceste tehnici.

Daca la intrarea coderului dicode se aplica o secventa de date, la iesire se obtine un semnal ternar. Un caz particular este ilustrat in figura 4.21.

Putem remarca ca fiecare front ascendent sau descendent din secventa de date de intrare X produce in semnalul codat Y un impuls pozitiv, respectiv negat Absenta tranzitiilor sau fronturilor se reflecta in producerea nivelului 0 la iesire.

Caracteristica de frecventa pentru codul biternar este:

(4.42)

prezentand zerouri pentru sau .

Se observa din figura 4.18 ca produce un nul spectral la frecventele , deci si la , respectiv si multiplii acesteia, iar produce nuluri spectrale la frecventele , deci multipli de , in particular si la frecventa zero.

Este evident ca folosind o functie F(D) sub forma unei combinatii de factori (1-D) si (1+D) se pot obtine proprietatile 1, 2 si 3 ale caracteristicii H(

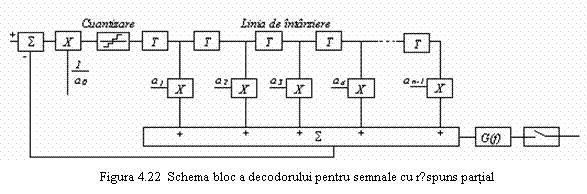
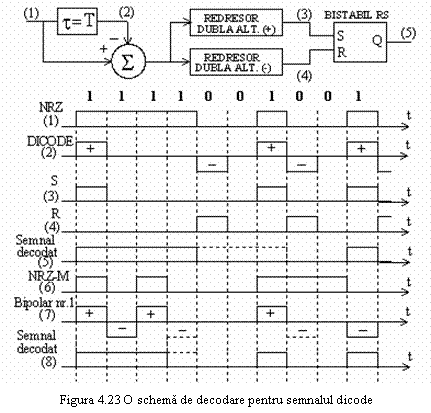
In figura 4.22 se prezintǎ schema bloc de principiu a circuitului decodor folosit pentru recuperarea informatiei transmise prin tehnica cu rǎspuns partial. Decodorul recupereazǎ informatia sub formǎ binarǎ, care se regǎseste in registrul de deplasare. Registrul de deplasare si sumatorul genereazǎ semnalul cu rǎspuns partial utilizat in transmisie iar circuitul codor astfel format are caracteristica de transfer H(f). Prin montarea sa in bucla de reactie se obtine caracteristica de transfer inversǎ, astfel cǎ circuitul complet functioneazǎ ca un decodor (functionare inversǎ codorului).

5 SRP cu precodare

Precodarea are drept scop eliminarea problemelor legate de propagarea erorii aparute la o decizie anterioara deci a interferentei intersimboluri. Pentru aceasta se intervine in emitator (sursa de date) suprimand efectul simbolurilor anterioare. Fie secventa de date definita de:

(modulo-m ) (4.43)

In general poate lua mai multe valori. Aceste valori redundante pot fi reduse prin interpretarea modulo-m a secventei de date . Simbolurile precodate si reduse modulo-m satisfac

(modulo-m) (4.44)

Coeficientii se presupun normalizati, avand valori intregi si cel mai mare divizor comun este unitatea. Ecuatia de mai sus are solutie unica daca si numai daca si m sunt numere prime intre ele. Ea poate fi scrisa ca:

(modulo-m) (4.45)

Sub aceasta forma se observa usor ca datele originale pot fi usor recuperate prin interpretarea modulo-m a semnalului receptionat, operatie ce nu implica memorizare.

Pentru semnale SRP cu spectru tip cosinus , valoarea esantionului la momentul este:

(4.46)

Pentru semnalele SRP cu spectru tip sinus, cu polinoame tip, si

(4.47)

respectiv: (4.48)

In ecuatiile de mai sus este valoarea esantionului din SRP in absenta zgomotului si poate lua valorile k si 0, iar este valoarea esantionului din semnalul de zgomot.

Cand , circuitul de precodare da in asa fel incat . Se observa ca semnalul SRP in acest caz este o codare pseudoternara (bitul 0 este reprezentat prin nivelul 0, iar bitul 1 prin nivele + si - ), iar decodarea se face foarte simplu prin redresare dubla alternanta. Semnalele SRP cu spectru tip sin² sunt descrise de polinomul:

(4.49)

Pentru SRP cu spectru tip sin² valoarea esantionului la momentul este:

(4.50)

Termenul reprezinta valoarea esantionului receptionat in conditii ideale (absenta zgomotului) si poate lua valorile -2k, -k, 0, +k, +2k.

Precodarea folosita pentru eliminarea interferentei intersimboluri presupune ca:

daca ,

, ,

iar poate fi unic determinat din in acest fel. Necesitatea precodarii poate fi mai usor inteleasa plecand de la codul dicode si schema sa de codare reprezentata in figurile 4.20 si 4.23. Tinand cont ca fronturile pozitive si negative din secventa de date genereaza impulsuri pozitive si respectiv negative in semnalul codat, se poate folosi ca decodor un bistabil de tip RS, care este setat de impulsurile pozitive si respectiv resetat de cele negative (figura 4.23). Putem remarca insa ca la aparitia unei erori, de exemplu nerecunoasterea unui impuls pozitiv sau negativ, bistabilul nu se mai seteaza, respectiv reseteaza in acel moment, iar secventa decodata ramane eronata pana la aparitia urmatorului impuls corect de setare sau respectiv resetare. In acest fel eroarea se propaga, de obicei pe mai multe intervale de bit.

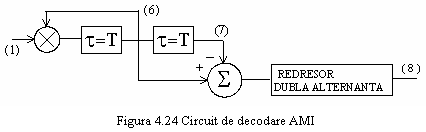Prin introducerea precodarii se vor asocia tranzitiile din secventa de date de intrare cu bitul 1 iar absenta lor cu bitul 0 (codare NRZ-M sau diferentiala). Se obtine astfel o forma de unda codata bipolar nr.1 sau AMI (Alternate Mark Inversion), in care bitul 1 este codat alternativ prin nivelele si , iar bitul 0 prin nivelul ternar 0.

Prin redresarea dubla alternanta a formei de unda codate se obtine secventa de date codata NRZ-L (figura 4.24). Daca in locul unui impuls negativ sau pozitiv s-a receptionat eronat nivelul 0, se observa este afectat de eroare numai bitul in cauza, nu si cei urmatori si s-a eliminat astfel prin precodare propagarea erorii. Formele de unda asociate pot fi urmarite din figura 4.23 si 4.24.

6 Semnale ternare in banda de baza.

Transmiterea digitala a informatiei pe o linie de telecomunicatii obisnuita implica un echipament de linie special, compus din echipamente terminale si regeneratoare intermediare.

Echipamentul de linie terminal are sarcina de a converti informatia digitala de intrare intr-un cod de linie, astfel incat semnalul transmis pe linie sa satisfaca urmatoarele cerinte:

performantele transmisiei sa fie pe cat posibil independente de caracteristicile statistice ale sursei de date,

jitterul introdus de repetor sa fie cat mai mic,

componenta de c.c. a fluxului de date emis sa fie nula, pentru a putea permite cuplarea in c.a. a repetoarelor pe linie,

sa permitǎ supravegherea performantelor in timpul functionarii.

Daca pentru transmisie se foloseste un cod binar unipolar, apar urmatoarele aspecte practice:

informatia de sincronizare trebuie extrasa din semnalul de date receptionat de fiecare repetor,

transmisia secventelor lungi de zero conduce la pierderea sincronizarii datorita absentei tranzitiilor, iar secventele lungi de biti 1 conduc la aparitia componentei de c.c.,

supravegherea functionarii transmisiei nu este posibila in formatul unipolar decat prin introducerea de biti redundanti care coboara viteza efectiva de transmisie si implica scaderea vitezei de transmisie pe linie fata de cea a datelor de intrare.

Un alt mod de introducere a redundantei, mult mai avantajos, este acela de a folosi un cod de transmisie ternar care elimina problemele practice discutate. In plus, codurile ternare permit obtinerea unui spectru al semnalului ce prezinta zerouri la anumite frecvente. Codurile ternare cele mai importante sunt: codurile bipolare nr. 1, 2 si 3, codul PST, codurile bipolare de densitate ridicata HDBn, codul 4B3T si codul MS 43.

6.1 Codurile bipolare nr. 1 si 2.

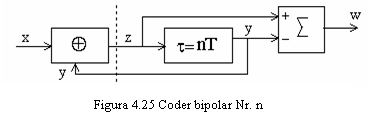Codurile bipolare fac parte din categoria codurilor pseudoternare, avand in vedere faptul ca asocierea dintre alfabetul binar si cel ternar este particulara. Astfel, considerand alfabetul binar compus din 0 si 1, iar cel ternar din -, 0 si +, bitul 0 binar este asociat intotdeauna cu 0 ternar, iar bitul 1 este codat alternativ prin + si -. Acesta conduce in mod evident la crearea unei componente de curent continuu nula.

Repetoarele nu mai sunt incarcate de componenta de c.c. si pot fi cuplate in c.a. la linie (prin condensator sau transformator). Codurile bipolare nr. n, (n=1, 2, 3) se obtin cu schema de principiu reprezentata in figura 4.25.

Spectrul semnalului de iesire w, poate fi usor dedus daca se cunoaste spectrul semnalului de intrare x. daca durata intervalului elementar binar este T, intarzierea cu nT este echivalenta cu o multiplicare a spectrului cu , iar functia de transfer a circuitului este .

Caracteristica de frecventa a circuitului din dreapta liniei punctate din figura 4.25 (denumit si coder DICODE) se obtine luand valoarea absoluta a functiei de transfer ridicatǎ la pǎtrat.:

(4.51)

iar (4.52)

Zerourile din spectru apar la , deci la frecventele .

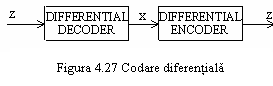
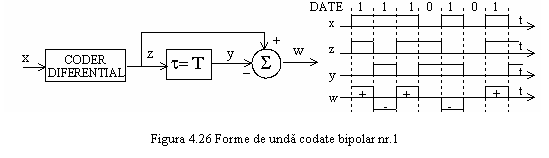
Codurile bipolare nr. 1, 2 si 3 se decodifica prin redresare dubla alternanta. Avand in vedere asocierea simbolurilor + si - de la iesirea coderului dicode cu tranzitiile din secventa de date, va trebui introdus un circuit de precodare, care converteste secventa de intrare x intr-o secventa z, egala cu suma modulo-2 dintre x si z intarziat cu un interval de bit. Pentru codul binar nr. 1, precodarea este diferentiala si obtinem schema din figura 4.26.

Se observa din figura 4.19 ca:

(4.53)

unde: reprezinta suma modulo-2, iar - semnalul intarziat cu T.

Sumand modulo-2 ambii membri ai relatiei cu obtinem

(4.54)

Deci, , sau x este un semnal echivalent cu z decodat diferential (mai putem spune ca z se obtine din x prin codare diferentiala), situatie prezentata in figura 4.27.

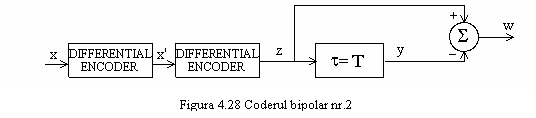
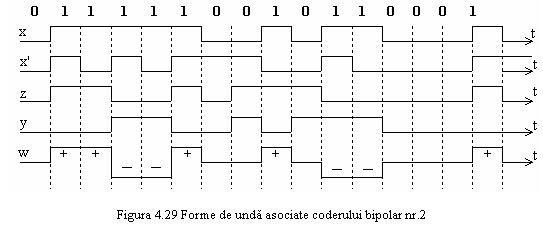
Codurile bipolare nr. 2 si 3 sunt similare cu codul bipolar nr. 1, insa intr-o secventa lunga de biti 1, primii n biti sunt codati prin n plusuri, iar urmatorii prin n minusuri. Codul binar nr. 2 este produs cu schema prezentata in figura 4.28, formele de unda fiind reprezentate in figura 4.29.

El este cel mai atractiv din punct de vedere al spectrului, caracteristica sa de frecventa fiind

(4.55)

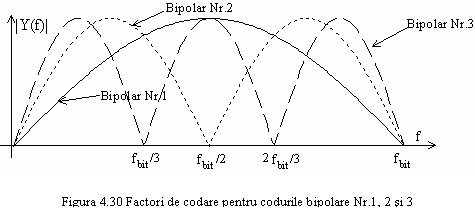
Ea este reprezentata in figura 4.30. Codul binar nr. 2 prezinta deci nuluri in spectru la frecventa zero si la frecvente multipli ai lui .

Se poate astfel transmite un semnal pilot pe frecventa purtatoare pentru a face posibila detectia sincrona a semnalului. De asemenea, se poate transmite un pilot pe frecventa , care sa faca independenta sincronizarea de bit de secventa binara de date transmisa.

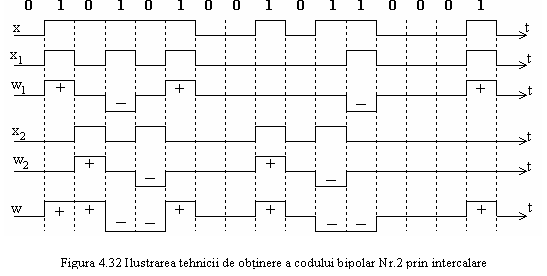
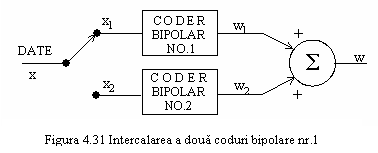
Codul binar nr. 2 poate fi produs si cu ajutorul schemei din figura 4.31, cele doua codoare bipolare fiind actionate de bitii 1 impari, respectiv pari; formele de unda asociate sunt reprezentate in figura 4.32.

6.2 Codul PST

Codarea ternara cu selectia perechilor (Paired Selected Ternary) implica impartirea arbitrara a secventei de date in grupe de 2 biti (dibiti) si codarea dibitilor prin perechi de simboluri ternare conform conventiei din tabelul 1.

Se observa ca perechile 11 si 00 reprezentate prin si respectiv au componenta continua nula. Pentru ca perechile 10 si 01 sa nu introduca componenta nula, s-a impus un al doilea mod de codare, astfel incat dupa o codare a lui 10 prin + 0, urmatorul dibit 10 sa fie codat prin - 0. In felul acesta anulandu-se componenta de c.c., ca in exemplul de mai jos:

Exemplul 1 Sa codam PST secventa de date x reprezentata mai jos

Sagetile indica optiunea facuta in codarea perechilor 1 0 si 0 1. Se observa ca exista cel mult doua zerouri consecutive, ceea ce favorizeaza sincronizarea.

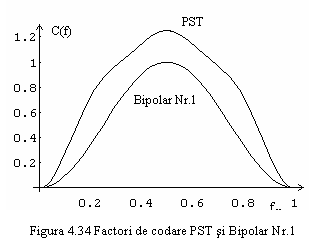
La pierderea sincronizarii, o secventa lunga de 0 poate fi interpretata ca o secventa lunga de 1 si invers. Factorii de codificare ai semnalelor PST si bipolar nr. 1 sunt ilustrate in figura 4.34.

6.3 Coduri bipolare de densitate ridicata HDBn

In codurile bipolare, bitul 0 binar este codat prin 0, iar bitul 1 este codat alternativ prin + si -, ceea ce asigura o componenta de c.c. nula. Sirurile lungi de zero pot conduce la pierderea sincronizarii, astfel incat pentru a evita aceasta situatie se poate actiona prin inlocuirea acestor secvente cu alte secvente care se caracterizeaza prin existenta unei violari a legii de codare bipolara. Se obtin astfel codurile bipolare de densitate ridicata HDBn (High Density Bipolar), cu n=2, 3, ..., n referindu-se la numarul maxim permis de zerouri succesive.

Daca notam cu B modul de codare al bitului 1 binar care se supune legii de codare binara si cu V violarea legii de codare bipolara (bitul 1 transmis este codat prin + daca bitul 1 anterior a fost codat prin +, sau prin -, daca anterior era - ), atunci regulile de codare pentru codul HDBn sunt:

bitul 1 este codat prin B,

bitul 0 intr-un bloc de maximum n zerouri succesive este codat prin 0,

un bloc de n+1 zerouri succesive este codat prin:

B0 .. V sau 00 ... V

Optiunea intre cele doua variante este determinata de necesitatea ca violarile succesive V sa fie de polaritati alternative, astfel incat componenta de c.c. sa ramana nula. Blocurile lungi de zerouri succesive sunt fragmentate in blocuri de n+1 zerouri si codate ca mai sus.

Cel mai important cod din aceasta categorie, HDB3, a fost acceptat de CCITT si este ilustrat mai jos:

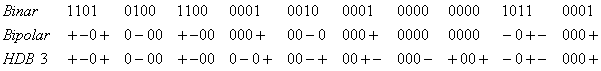
V B V V B V

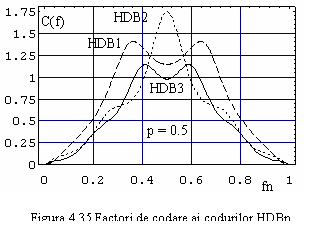Factorii de codare ai codurilor HDB 1, 2 si 3 sunt prezentati in figura 4.35.

O varianta a codului HDBn este CHDBn (Compatible HDBn), in care secventa prin care este codat un bloc de n+1 zerouri succesive ia una din formele:

a. 00 .. 000 V sau

b. 00 ...0B0V

Avantajul acestor coduri e acela ca se poate proiecta decodorul independent de n.

6.4 Codurile 4B3T si MS 43

Ambele coduri sunt alfabetice si convertesc blocuri de 4 simboluri binare in blocuri de 3 simboluri ternare, conform tabelelor 2 si 3.

Aceste coduri sunt interesante pentru comunicatiile digitale, avand in vedere reducerea vitezei de transmisie a simbolurilor ternare la din cea a unui semnal binar clasic.

Tabelul 2 Codul 4B3T Tabelul 3 Codul MS 43

Codurile folosesc 3 alfabete: R1, R2 si R3, selectarea lor facandu-se in functie de valoarea sumei digitale curente a codului. Numarul de simboluri succesive de aceeasi valoare este limitat la 6 pentru codul 4B3T si 3 pentru MS 43. In cazul 4B3T, din cele 6 setari (0 - 5), cele extreme apar numai in interiorul cuvintelor de 3 cifre ternare si se asociaza starea 1 cu R1, 2 si 3 cu R2 si 4 cu R3.

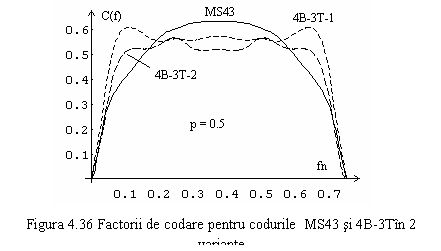
Sincronizarea de bloc poate fi usor monitorizata, pierderea ei conducand la aparitia unor combinatii interzise, cum ar fi 000 in cazul codului 4B3T. Spectrele de putere ale celor 2 coduri sunt reprezentate in figura 4.36. 

Exemplul 2 Sa decodam secventa de date codata HDB4, data mai jos si sa calculam:

a. Probabilitatea de aparitie a violurilor de bipolaritate in semnalul HDB3, presupunand bitii 1 si 0 echiprobabili;

b. Cu cat creste puterea medie a semnalului codat HDB4 fata de codul bipolar nr. 1.

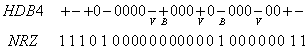
Un viol de bipolaritate apare daca si numai daca:

Un bit 0 este precedat de 3 zerouri,

Un bit 0 este precedat de 7 zerouri,

Un bit 0 este precedat de 11 zerouri, etc.

Daca jumatate din violurile de bipolaritate sunt insotite de o marca bipolara (B000V), iar bitii 0 si 1 sunt echiprobabili, cresterea relativa a puterii semnalului este

7. Aleatorizarea secventei de date.

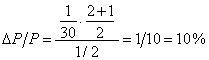
Spectrul de frecventa al unui semnal de date depinde de codul folosit pentru transmisie si de succesiunea de biti 1 si 0 din secventa de date. Datele contin adesea secvente periodice care duc la aparitia in spectru a componentelor discrete (linii) care pot constitui semnale de interferenta foarte periculoase pentru canalele alaturate.

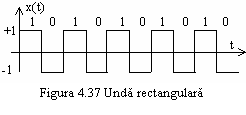
Considerand o secventa de tipul 101010, ea este echivalenta cu o unda rectangulara de frecventa , cu nivelele , ca in figura 4.37.

Descompunand in serie Fourier, obtinem:

(4.56)

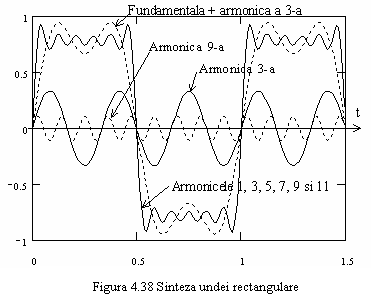
Suma sinusurilor este ilustrata in figura 4.38, pentru primele 5 armonici (pana la armonica 11).

Calculand nivelul relativ al armonicii a 3-a fata de puterea semnalului, pentru rezistenta de sarcina avand valoarea egala cu un ohm:

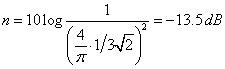
(4.57)

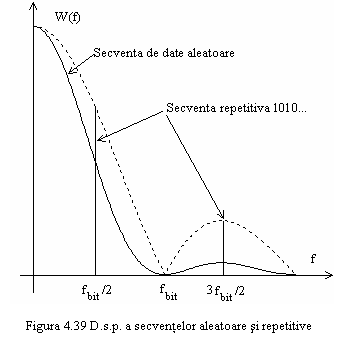
Spectrul de putere normalizat, pentru o rezistenta de sarcina de 1 ohm, al unei secvente de date NRZ aleatoare este dat de

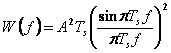(4.58)

si este reprezentat in figura 4.39. Semnalul de date aleator nu prezinta in spectrul sau componente discrete.

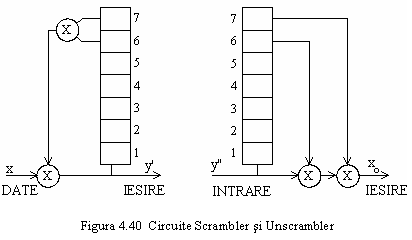
Sumand modulo-2 secventa de date repetitiva cu o secventa binara pseudoaleatoare se obtine o reducere drastica a amplitudinilor componentelor discrete din spectru. Blocul care realizeaza aceasta functie se numeste SCRAMBLER (aleatorizor sau cifrator) si are schema bloc de principiu prezentata in figura 4.40, conform avizului V 27 al CCITT.

El se compune dintr-un registru de deplasare cu reactie ce genereaza o secventa binara pseudoaleatoare cu lungimea: (127) biti.

La receptie, un dispozitiv UNSCRAMBLER (descifrator) executa operatiile inverse celor de la emisie si astfel se obtine secventa de date originala.

Se observa ca un bit eronat izolat care strabate descifratorul, aparand pe rand la fiecare din iesirile 6 si 7, produce 2 biti suplimentari de eroare. Asadar, un bit eronat produce un grup de 3 erori in secventa de date de iesire D, deci un efect finit.

Daca la intrare se aplica secventa de date D, compusa din zerouri, iar registrul contine zerouri, secventa de iesire D e de asemenea compusa din zerouri. Aceasta situatie este inlaturata folosind un contor de coincidenta care injecteaza un bit 1 suplimentar in bucla dupa o secventa lunga de 1 sau 0.

Pentru a putea explica functionarea schemei, sa introducem operatorul D, care semnifica intarzierea secventei de date. Astfel, xD reprezinta secventa de date x intarziata cu 1 bit iar , secventa x intarziata cu k intervale de bit.

Pentru circuitul UNSCRAMBLER putem scrie:

(4.59)

unde . Atunci pentru SCRAMBLER vom avea:

sau (4.60)

in absenta erorilor , iar la iesire avem:

(4.61)

adica secventa de iesire din UNSCRAMBLER coincide cu cea de intrare in SCRAMBLER.

Efectul SCRAMBLER-ului asupra secventelor periodice si a sirurilor lungi de 1 sau 0 poate fi observat din tabelul 4, scris in ipoteza ca registrul este incarcat initial cu 0.

Se observa ca SCRAMBLER-ul elimina efectiv secventele lungi de 0 si 1, precum si secventele periodice.

8 Filtre standard utilizate in telecomunicatii

Conform criteriului I al lui Nyquist, transmisia practica a semnalelor in banda de baza, fara interferenta intersimboluri (IIS), se poate face utilizand filtre trece-jos a caror functie de transfer sa prezinte simetrie impara in jurul frecventei de taiere, ele fiind realizabile fizic. Raspunsul lor de tip Nyquist este definit cu ajutorul unor functii standard definite in continuare.

Functia rectangulara

(4.62a)

A. Functia sinc

(4.62b)

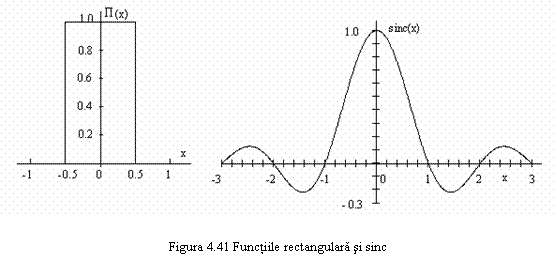
Functiile si sinc(x) constituie perechi Fourier si sunt reprezentate in figura 4.41.

Functia sinc cu factor de cadere

(4.63)

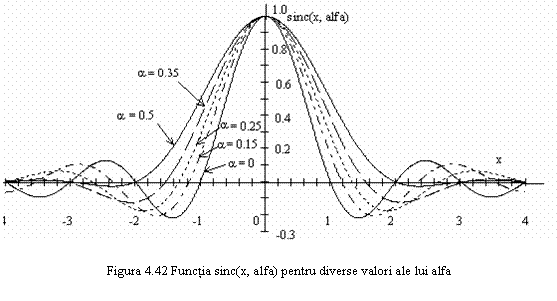
In figura 4.42 sunt reprezentate functiile pentru diferite valori ale lui intre 0 si 0.5. Cazul ne da functia sinc(x) clasica.

Functia cosinus ridicat Rc (Raised Cosine)

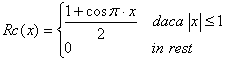(4.64)

B. Functia cosinus ridicat Rc cu factor de cadere

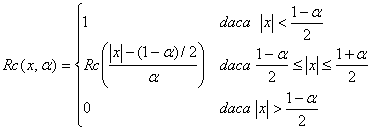(4.65)

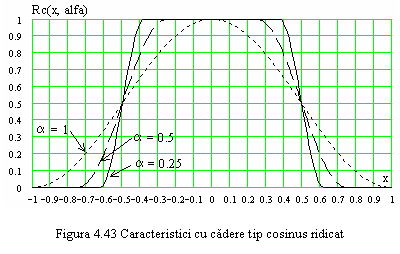
In figura 4.43 sunt prezentate cateva caracteristici pentru unele valori ale lui . Cazul corespunde lui de la punctul D.

Se observa ca filtrele RC introduc o crestere a benzii fata de banda B, pe care sa o notam cu , iar banda transmisiei devine

sau

Tinand cont ca in banda B se poate face o transmisie cu viteza de bit , ( a se vedea formula 4.13) iar este cresterea relativa a benzii si se noteaza cu , avem

Notand cu viteza de transmisie a datelor, se observa ca viteza maxima posibila de realizat in cazul utilizarii filtrului de tip cosinus ridicat si unei benzi de transmisie este

(4.66)

9 Distribuirea caracteristicii spectrale intre emisie si receptie

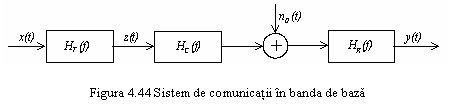
Fie schema bloc simplificata a unui sistem TD in banda de baza cea reprezentata in figura 4.44, unde este semnalul aplicat la intrarea filtrului de emisie , - caracteristica canalului, functia de transfer a filtrului de receptie, iar zgomotul, considerat aditiv si gaussian.

Caracteristica spectrala globala a acestui sistem este

(4.67)

si se alege in asa fel incat sa indeplineasca primul criteriu al lui Nyquist in ceea ce priveste lipsa IIS. Ea va lua deci forma unui "cosinus ridicat", care trebuie realizat din contributia celor doua filtre de la emisie si receptie.

Pentru un sistemul de TD in banda de baza vom determina alegerea optima a caracteristicilor filtrelor de emisie si receptie , in asa fel ca sa se respecte probabilitatea de eroare impusa pentru o viteza specificata de transmisie a datelor , puterea emisa , densitatea spectrala a zgomotului , caracteristica canalului precum si densitatea spectrala de putere a datelor dupa filtrul de receptie . Deci, si vor fi alese in asa fel incat raportul semnal/zgomot la iesirea filtrului de receptie sa fie maxim, iar probabilitatea de eroare minima.

Evident, pentru usurinta realizarii celor doua filtre, cel mai simplu este cazul , adica exceptand o anumita constanta, caracteristicile celor doua filtre sa fie identice, ceea ce usureaza proiectarea si constructia echipamentului.

In general, caracteristica canalului este cunoscuta, iar pentru cazul idealizat se presupune . Minimizarea probabilitatii de eroare este echivalenta cu maximizarea raportului S/Z.

Impulsurile care se aplica filtrului de emisie ponderate cu datele echiprobabile, au o durata mai mica sau egala cu si sunt emise in mod independent.

(4.68)

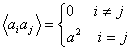(4.69)

iar dupa filtrul de receptie acestea devin , a caror transformata Fourier este . Conform ec. (4. 67) intre si exista relatia:

(4.70)

unde este o constanta de normalizare iar este timpul de propagare prin sistem.

Densitatea spectrala de putere a lui este:

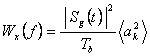(4.71)

iar densitatea spectrala a semnalului emis este

(4.72)

Notand cu densitatea spectrala a zgomotului la intrarea in receptor, la iesirea receptorului vom avea o putere de zgomot:

(4.73)

Iesirea filtrului de receptie la momentul de esantionare este

(4.74)

daca amplitudinea semnalului receptionat la momentul este . Iesirea filtrului va fi 0 sau 1 dupa cum sau .

Fie decizia care se ia cu privire la cel de al m-lea bit. Evident, decizia corecta apare ca:

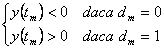(4.75)

Erorile pot apare daca:

, eveniment notat cu , sau

, eveniment notat cu .

Notand , probabilitatea de eroare este data de

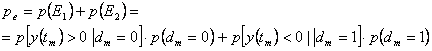(4.76)

Pentru o transmisie echiprobabila

Conform relatiei (4.71), atunci cand se iau deciziile corecte, valorile lui devin:

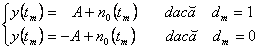(4.77)

unde . Dar conform rel.(4.74),

iar relatia (4.73) devine

(4.78)

Utilizand relatia (4.75) si tinand cont ca zgomotul are dispersia , iar puterea sa este , fiind data de relatia (4.70) putem scrie (4.78) sub forma:

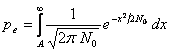(4.79)

sau utilizand schimbarea de variabila

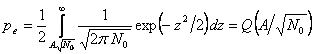(4.80)

unde 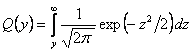(4.81)

Puterea semnalului de la intrarea in canal este

(4.82)

Tinand cont de relatia (4.66) atat pentru amplitudinea unui impuls cat si pentru media lor, putem scrie relatia:

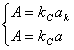(4.83)

Din relatia (4.83) si inlocuind in (4.79) rezulta:

(4.84)

de unde 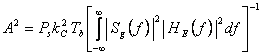(4.85)

Valoarea raportului S/Z este deci tinand cont de (4.85) si (4.73):

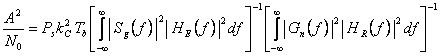(4.86)

Va trebui deci minimizata expresia:

(4.87)

Cum , sunt cunoscute, minimizarea expresiei cu privire la variabilele si poate fi facuta aplicand inegalitatea lui Schwartz. Se stie ca daca si sunt doua functii complexe de f, atunci:

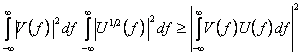(4.88)

Valoarea minima a membrului doi se obtine atunci cand

(4.89)

unde k este o constanta arbitrara. Luand:

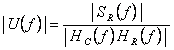(4.90)

atunci minimumul expresiei considerate se obtine cand:

(4.91)

de unde, in mod analog pentru filtrul de emisie, rezulta:

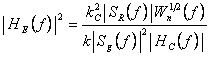(4.92)

Cele doua filtre pot avea caracteristici de faza arbitrare, cu conditia ca acestea sa se compenseze. Valoarea maxima a raportului S/Z la iesirea filtrului de receptie (inaintea circuitului de esantionare este:

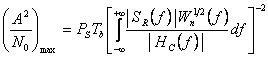(4.93)

si in acest caz probabilitatea de eroare este:

(4.94)

Sa consideram cazul particular cand densitatea spectrala de putere a zgomotului este plata. . Atunci, conform (4.91) si (4.92),

(4.95)

unde si sunt doua constante pozitive. Deci

(4.96)

Proiectarea unui sistem de TD cu modulatia impulsurilor in amplitudine (PAM) inseamna deci a specifica forma impulsurilor si , functia de transfer a filtrului de emisie si receptie precum si nivelul de putere al semnalului emis , pentru a realiza valoarea impusa a probabilitatii de eroare .

Daca presupunem ca viteza de transmisie a datelor este atunci se impun o serie de observatii cu privire la latimea B a benzii canalului de transmisie, presupus de forma unui FTJ, ce satisface conditia

(4.97)

Daca , atunci se poate recurge la o transmisie multinivel cu M nivele, de amplitudine. Daca , atunci se poate folosi o modulatie neliniara sau tehnici cu spectru extins pentru reducerea efectului zgomotului asupra semnalului.

Datorita necesitatii de a distribui in mod egal caracteristica filtrului de tip cosinus ridicat intre emisie si receptie, vom utiliza atat la emisie cat si la receptie filtre cu caracteristica de tip

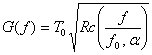(4.98)

care in domeniul timp vor avea raspunsuri la impuls de forma

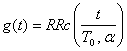(4.99)

RRc reprezentand functia Root-Raised-cosine (radical din cosinus ridicat) si este definita ca

(4.100)

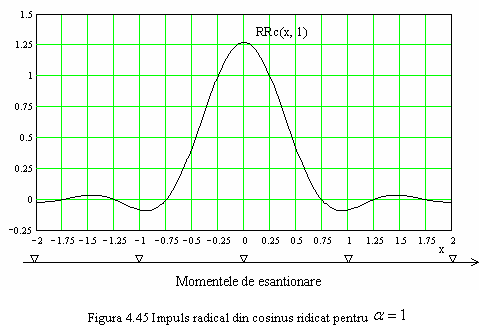
Ea este reprezentata in figura 4.45 pentru . Se observa ca filtrul tip radical din cosinus ridicat introduce interferenta intersimboluri, valoarea semnalului fiind diferita de zero la momentele de esantionare.

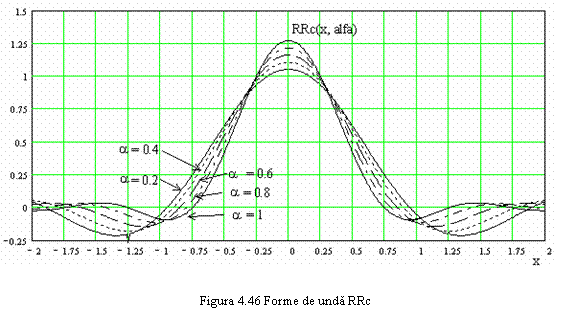
In figura 4.46 sunt reprezentate alte forme de unda tip RRc, pentru diverse valori ale lui . La receptie se foloseste un filtru identic, combinatia celor doua filtre producand in conditii ideale un raspuns ce satisface criteriul I al lui Nyquist. In conditii reale se observa in continuare prezenta interferentei intersimboluri, ceea ce face necesara introducerea egalizarii la receptie.

IV Transmisii in banda de baza

1 Criteriul I Nyquist

2 Criteriul II Nyquist

3 Criteriul III Nyquist

4 Semnale cu raspuns partial SRP

5 SRP cu precodare

6 Semnale ternare in banda de baza

6.1 Codurile bipolare nr.1

6.2 Codul PST

6.3 Codurile bipolare de densitate ridicata HDBn

6.4 Codurile 4B3T si MS43

7 Aleatorizarea secventei de date

8 Filtre standard utilizate in telecomunicatii

9 Distribuirea caracteristicii spectrale intre emisie si receptie