| CATEGORII DOCUMENTE |
| Gradinita |
Proiect didactic
Scoala Generala "Geo Bogza" - Balan
Clasa a VII-a
Profesor:
Obiectul :MATEMATICA
Subiectul: Relatii metrice in triunghiul dreptunghic
Tipul lectiei: de insusire de noi cunostinte
Obiective generale:
Obiective operationale:
Colaborarea si cooperare in grupe;
Exersarea abilitatilor de lucru in echipa;
Metode si procedee:
Munca in echipa;
Metoda Mozaic;
Colaborarea;
Resurse:
de timp: 50 min.
umane: clasa de nivel bun, step by step, de 24 elevi;
materiale: fise pentru experti, fise de lucru, instrumente geometrice.
Desfasurarea activitatii
1. Momentul organizatoric
Salutul, prezenta, verificarea temei.
2. Evocarea
Se imparte clasa in patru grupe, folosind cartonase colorate. Pe fiecare masa de lucru se aseaza cartoane cu numere, de la 1 la 4, ce vor arata grupele de lucru. In fiecare grup, elevii isi vor alege un numar de la unu la patru, precizandu-li-se ca vor trebui sa se ridice si sa se aseze la masa pe care este asezat numarul ales de ei. Se vor forma astfel 4 grupe de experti. Li se explica elevilor ca vor deveni experti in grupa, si vor primi cate o fisa de lucru pe care dupa 15 minute vor trebui sa o explice colegilor din grupele initiale. Se impart fisele de experti, elevii le discuta in grup, profesorul monitorizeaza activitatea fiecarei grupe.
Dupa 15 minute, se refac grupele initiale, in care vor exista experti in fiecare teorema. Fiecare expert, explica celorlalti colegi, teorema invatata, colegii notand pe caiete. Dupa 15 minute, fiecare elev, va avea toate teoremele explicate. Profesorul intervine ori de cate ori simte ca este nevoie.
Se impart fise de lucru si elevii vor trebui sa aplice pe rand, teoremele invatate, in rezolvarea de probleme. Se lucreaza in grupe. Dupa 10 minute, cate un raportor din fiecare grupa prezinta solutiile obtinute.
3. Reflexia
Se cere elevilor sa completeze urmatoarea afirmatie: " Daca as fi o teorema, intr-un triunghi dreptunghic, mi-ar placea sa fiu teorema....... deoarece...........".
Se face evaluarea notand elevii care s-au remarcat, se scrie pe tabla tema pentru. acasa.
Fisa de experti 3:Teorema lui Pitagora
B
Desenati un triunghi dreptunghic ABC, cu m(A)=90.

Teorema lui Pitagora:Intr-un triunghi dreptunghic, patratul lungimii ipotenuzei este egal cu suma patratelor lungimilor catetelor.
BC² = AB² + AC²
OBS: - teorema se demonstreaza scriind teorema catetei pentru fiecare cateta si adunand relatiile.
Aplicatie:
In triunghiul dreptunghic ABC, m(A)= 90, AB=4 cm si AC= 3 cm. Sa se determine lungimea ipotenuzei.
Fisa de experti 1 Teorema inaltimii
Desenati un triunghi dreptunghic ABC si construiti
inaltimea corespunzatoare ipotenuzei.
B
 Care
sunt proiectiile catetelor pe ipotenuza? Scrieti-le.
Care
sunt proiectiile catetelor pe ipotenuza? Scrieti-le.
Teorema inaltimii: Intr-un triunghi dreptunghic, patratul lungimii inaltimii corespunzatoare ipotenuzei este egal cu produsul lungimilor segmentelor determinate de ea pe ipotenuza. AD²=BD.DC
Obs: Teorema se demonstreaza scriind asemanarea triunghiurilor ABD si CAD.
Aplicatie: In triunghiul ABC m(A)=90, AD![]() BC, D
BC, D![]() BC, cunoastem: DC=63 cm. si BC = 70 cm. Calculati lungimile
segmentelor BD si AD.
BC, cunoastem: DC=63 cm. si BC = 70 cm. Calculati lungimile
segmentelor BD si AD.
Fisa de experti 4 Teorema
Desenati
un triunghi dreptunghic si construiti inaltimea corespunzatoare ipotenuzei.
B

Teorema: Intr-un triunghi dreptunghic, lungimea inaltimii corespunzatoare ipotenuzei este egala cu catul dintre produsul lungimilor catetelor si lungimea ipotenuzei.
AD = ![]()
Obs: Teorema se demonstreaza scriind aria triunghiului ABC in doua moduri.
Aplicatie:
In triunghiul dreptunghic ABC, m(A)=90, m(B)=30, construim AD![]() BC, D
BC, D![]() BC. Daca AC = 5 cm, AB = 6 cm , calculati lungimea inaltimii
corespunzatoare ipotenuzei.
BC. Daca AC = 5 cm, AB = 6 cm , calculati lungimea inaltimii
corespunzatoare ipotenuzei.
Fisa de experti 2 Teorema catetei
A
Desenati un triunghi dreptunghic ABC, m(A)=90.Construiti AD
![]() BC, D
BC, D![]() BC .
BC .
B

Teorema catetei: Intr-un triunghi dreptunghic, patratul lungimii unei catete este egal cu produsul dintre lungimea ipotenuzei si lungimea proiectiei catetei pe ipotenuza.
AB² = BC.BD sau AC² = BC.DC
Obs.: Teorema se demonstreaza folosind asemanarea triunghiurilor.
Aplicatie: In triunghiul dreptunghic ABC, m(A)= 90, AB=4 cm. si BD=3 cm. Aflati lungimea ipotenuzei si lungimea celeilalte catete.
Fisa de lucru
1. In triunghiul ABC,
m(A)=90, AD![]() BC, AD=12cm.,BD = 9cm. Se cer CD, AB, AC, BC.
BC, AD=12cm.,BD = 9cm. Se cer CD, AB, AC, BC.
2. In triunghiul ABC,
m(A)=90, AD![]() BC, AB=36cm, BC=60cm. Se cer BD, CD, AC, AD.
BC, AB=36cm, BC=60cm. Se cer BD, CD, AC, AD.
3. In triunghiul ABC,
m(A)=90,m(B)=30, AD![]() BC, AD=4cm.Se cer : DB, DC, AC, AB.
BC, AD=4cm.Se cer : DB, DC, AC, AB.
4. In triunghiul ABC,
m(A)=90, AD![]() BC, notam BD=x, CD=y, BC=a, AB=c, AC=b, AD=h. Daca
BC, notam BD=x, CD=y, BC=a, AB=c, AC=b, AD=h. Daca 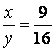 , a=25 cm, se cer x, y, b, c, h.
, a=25 cm, se cer x, y, b, c, h.
Fisa de lucru
1.In triunghiul ABC,
m(A)=90, AD![]() BC, AD=12cm.,BD = 9cm. Se cer CD, AB, AC, BC.
BC, AD=12cm.,BD = 9cm. Se cer CD, AB, AC, BC.
2. In triunghiul ABC,
m(A)=90, AD![]() BC, AB=36cm, BC=60cm. Se cer BD, CD, AC, AD.
BC, AB=36cm, BC=60cm. Se cer BD, CD, AC, AD.
3. In triunghiul ABC, m(A)=90,m(B)=30,
AD![]() BC, AD=4cm.Se cer : DB, DC, AC, AB.
BC, AD=4cm.Se cer : DB, DC, AC, AB.
4. In triunghiul ABC,
m(A)=90, AD![]() BC, notam BD=x, CD=y, BC=a, AB=c, AC=b, AD=h. Daca
BC, notam BD=x, CD=y, BC=a, AB=c, AC=b, AD=h. Daca 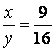 , a=25 cm, se cer x, y, b, c, h.
, a=25 cm, se cer x, y, b, c, h.
Fisa de lucru
1. In triunghiul ABC, m(A)=90, AD![]() BC, AD=12cm.,BD = 9cm. Se cer CD, AB, AC, BC.
BC, AD=12cm.,BD = 9cm. Se cer CD, AB, AC, BC.
2. In
triunghiul ABC, m(A)=90, AD![]() BC, AB=36cm, BC=60cm. Se cer BD, CD, AC, AD.
BC, AB=36cm, BC=60cm. Se cer BD, CD, AC, AD.
In triunghiul ABC,
m(A)=90,m(B)=30, AD![]() BC, AD=4cm.Se cer : DB, DC, AC, AB.
BC, AD=4cm.Se cer : DB, DC, AC, AB.
In triunghiul ABC, m(A)=90, AD![]() BC, notam BD=x, CD=y, BC=a, AB=c, AC=b, AD=h. Daca
BC, notam BD=x, CD=y, BC=a, AB=c, AC=b, AD=h. Daca 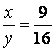 , a=25 cm, se cer x, y, b, c, h.
, a=25 cm, se cer x, y, b, c, h.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 5881
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved