| CATEGORII DOCUMENTE |
| Animale | Arta cultura | Divertisment | Film | Jurnalism | Muzica |
| Pescuit | Pictura | Versuri |
ANTROPOMETRIE
SCOP
Definitie: Ramura de baza a antropologiei care studiaza dimensiunile fizice, proportiile si compozitia corpului uman in scopul determinarii diferentelor la nivel individual si de grup.
In vederea descrierii si diferentierii caracteristicilor de rasa, sex, virsta si constitutie corporala sunt necesare masuratori fizice diverse.
In trecut accentul major al acestor studii era de natura evolutiva sau istorica. In ultimul timp, totusi, aceste studii au crescut in importanta, fiind necesare in proiectarea interfetelor om-masina, a spatiilor de lucru si a echipamentelor. Multe din aceste necesitati sunt rezolvate prin masuratori simple, liniare de suprafata sau volum.
In analiza miscarii umane sunt necesare, totusi, masuratori cinematice precum si determinarea maselor, a momentelor de inertie si a pozitiei lor. Acestora li se adauga si un corp restrins de cunostiinte ce se refera la centrele de rotatie ale articulatiilor, originea si insertia muschilor, unghiurile de actiune a tendoanelor, lungimea si sectiunea muschilor.
DIMENSIUNILE SEGMENTELOR
Dimensiune de baza a corpului uman o constituie lungime segmentelor intre fiecare dintre articulatii. Acestea variaza functie de constitutia corporala, de sex si rasa.
Dempster si colaboratorii sai (1955, 1959) au rezumat estimarile lungimilor si pozitiile centrului de rotatie a articulatiilor relativ la puncte corespunzind unor repere anatomice.
Date cu privire la lungimile segmentelor, exprimate ca procente din inaltimea corpului au fost stabilite de Drills si Contini(1966)- fig.1.
Aceste proportii ale segmentelor servesc drept o buna aproximatie in absenta unor informatii mai bune, preferabil masurate direct pe individ.
1.3 DENSITATE, MASA SI PROPRIETATI INERTIALE
Analizele kinematice si kinetice cer date privind:
centrele de masa,
momentele de inertie;
distributia maselor.
Unele dintre aceste masuratori au fost determinate pe cadavre; altele au utilizat volumele segmentelor masurate in combinatie cu tabele de densitate iar tehnicile moderne folosesc sisteme de scanare care furnizeaza imagini transversale multiple preluate de-a lungul unui segment( tehnica tomografica).
DENSITATEA INTREGULUI CORP
Corpul uman consta din mai multe tipuri de tesuturi, fiecare cu o densitate diferita.
De exemplu, greutatile specifice pentru diferite structurianatomice sunt:
osul cortical : g > 1,8;
tesutul muscular: g
tesutul gras: g < 1.
Densitatea medie este functie de constitutia corporala, numita somatotip.
Drills si Contini (1966) au dezvoltat pentru densitatea d a corpului o expresie ce este data ca o functie a indicelui ponderal c.
Acest indice ponderal are expresia :
c = ![]() [1]
[1]
in care : w = masa corpului ( in pounds);
h = inaltimea corpului ( in inchi).
In cazul utilizarii sistemului anglo-saxon de unitati de masura, expresia densitatii are forma:
r = o.69
+ 0.0297 c [ ![]() [2]
[2]
Expresia echivalenta in S.I. este :
r = 0.69 + 0.9 c [ kg/l] [2']
in care: w - [kg]
h - [m]
Se poate vedea ca o persoana scunda si grasa are un indice ponderal mai scazut decit o persoana inalta si slaba si deci are o densitate corporala mai mica.
Exemplul 1.
Pentru o persoana avind
inaltimea h =
c = h/![]() = 70/
= 70/ ![]()
Densitatea va fi in acest caz :
d = 0.69 + 0.0297 c = 0.69 + 0.0297 x 12.64 = 1.065 kg/l]
In S.I. :
h = 70/ 39.4 = ![]() = 0.418
= 0.418
w = 170 / 2.2 =
Pentru densitate se va obtine :
d = 0.69 + 0.9 c = 0.69 + 0.9 x 0.418 = 1.066 kg/l
DENSITATILE SEGMENTELOR
Fiecare segment corporal are o combinatie unica de oase, muschi, grasime si alte tesuturi, iar densitatea in interiorul unui anumit segment nu este uniforma. In general, datorita proportiei mai mari de oase, densitatile segmentelor distale este mai mare decit a celor proximale iar segmentele individuale isi cresc densitatile dupa cum creste densitatea medie a corpului.
Figura 2 prezinta aceste tendinte pentru sase segmente ca functie de densitatile corporale callculate cu ecuatiile [1] si [2] sau masurata direct ( Drillis si Contini 1966; Contini 1972).
1.3.3 MASA SEGMENTULUI SI CENTRUL SAU DE MASA
Termenii de centru de masa sau centru de greutate sunt deseori utilizati unul in locul altuia.
Termenul mai general este de centru de masa, in timp ce centrul de greutate se refera la centrul de masa pe o singura directie, cea definita de directia fortei de greutate. Pentru celelate doua axe, din plan orizontal, trebuie utilizat termenul de centru de masa.
Cresterea masei corpului determina si cresterea masei fiecarui segment, ca procent din masa corpului. Tabelul 1 rezuma rezultatele compilarilor mai multor investigatori. Aceste valori sunt utilizate in toate exemplele ce vor fi prezentate.
Pozitia centrului de masa este data, de asemenea ca procent al lungimii segmentului fata de capatul distal sau proximal.
In studiile efectuate pe cadavre determinarea centrului de masa se
efctueaza simplu, prin determinarea centrului de echilibru al fiecarui segmnt.
Pentru calcularea centrului de masa in vivo este necesar a se cunoaste profilul
ariei transversale si lungimea segmentului.
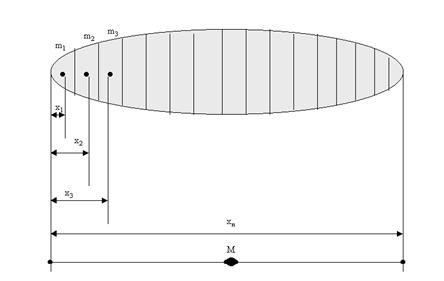
Pentru un profil ipotetic (fig. 3), divizat in n sectiuni, fiecare avind masa mI , masa totala va rezulta ca fiind :
M = ![]() I
I
in care : mI
= dI VI ![]() cu dI = densitatea sectiunii i;
cu dI = densitatea sectiunii i;
VI = volumul sectiunii i.
Daca densitatea d se presupune a fi uniform distribuita pe segment atunci :
mi
= ![]() deci M = d
deci M = d ![]() [4]
[4]
Centrul de masa trebuie sa fie astfel incit sa creeze acelasi moment al fortei de greutate in jurul oricarui punct de-a lungul axei segmentului ca si masa distribuita initial.
Considerind centrul de masa localizat la o distanta x de capatul din stinga al segmentului, se poate scrie :
![]() de
unde rezulta :
de
unde rezulta : 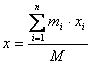 [5]
[5]
Se poate reprezenta masa distribuita printr-o singura masa M pozitionata la o distanta x de unul din capetele segmentului.
Din datele antropometrice prezentate in tabelul 1 sa se calculeze coordonatele centrului de masa pentru picior si coapsa, stiind coordonatele urmatoarelor repere anatomice:
glezna : ( 84.9;11.0);
metatarsiene: ( 101.1; 1.3);
marele rohanter: ( 72.1; 92.8);
condilul femoral lateral: ( 86.4; 54.9).
Din tabelul 1 rezulta ca centrul de masa al piciorului este la 0.5 din distanta dintre maleola laterala si reperul de pe metatarsiene. Deci centrul de masa al piciorului se obtine ca fiind dat de urmatoarele coordonate:
X = 84.9 + ( 101.1 - 84.9 ) . 0.5 =
Y = 1.3
+ (11 - 1.3). 0.5 =
Centrul de masa al coapsei se afla comform tabelului 1 la 0.433 de capatul proximal al segmentului. Deci centrul de masa al coapsei se obtine ca fiind dat de urmatoarele coordonate:
X = 72. + 0.433. ( 86.4 - 72.1) = 78.3;
1.3.4 CENTRUL DE MASA AL UNUI SISTEM DE SEGMENTE
Cu fiecare segment in miscare centrul de masa al intregului corp este variabil in timp. Este, deci necesar calcularea lui dupa fiecare interval de timp, ceea ce impune cunoasterea traiectroiilor centrului de masa pentru fiecare segment al corpului.
Se considera pentru un anumit moment de timp un sistem de trei segmente cu centrele de masa indicate ca in fig. 4.
Centrul de masa al intregului sistem este localizat in ( x0, y0 ) si fiecare din aceste coordonate pot fi calculate separat:
M = m1+ m2 + m3 si x0 = ![]() y0
=
y0
=![]() [6]
[6]
Centrul de masa al intregului corp este o variabila frecvent calculata. Utilitatea ei in evaluarea miscarii umane este oarecum limitata. Unii cercetatori utilizeaza variatia in timp a centrului
de masa pentru a calcula variatiile de energie ale intregului corp. Un astfel de calcul este insa eronat pentru ca centrul de masa nu conteaza in variatiile de energie relative la miscarile
 |
reciproce ale segmentelor membrelor. Astfel, variatiile de energie asociate cu miscarea inainte a unui picior si cea inapoi a celuilalt picior nu vor fi detectate prin centrul de masa care poate ramine relativ neschimbat.
Utilizarea majora a centrului de masa este in analiza activitatilor sportive, in special a sariturilor, unde traiectoria centrului de masa este critica pentru succesul actiunii pentru ca este decisa in chiar momentul startului( al desprinderii). Pozitia centrului de masa este de asemenea importanta in studiile privind postura si echilibrul corpului.
MOMENTUL DE INERTIE SI RAZA DE GIRATIE
Localizarea centrului de masa pentru fiecare segment este necesara pentru analiza miscarii de de translatie in spatiu. Daca sunt implicate acceleratii este necesara cunoasterea rezistentei inertiale la astfel de miscari.
In cazul miscarii liniare relatia dintre forta si acceleratia rezultanta este descrisa de relatia:
F = m![]()
M = I![]()
Constanta de proportionalitate dintre momentul M si acceleratia unghiulara produsa de acesta reprezinta abilitatea segmentului de a se opune modificarilor in viteza unghiulara.
Unitatile de masura sunt cele cunoscute :
M = [ N.m] , e = [ rad/sec2 ] , I = [ kg.m2 ]
Valoarea lui I depinde de punctul injurulcaruia are loc rotatia si este minima cind rotatia are loc in jurul centrului de masa.
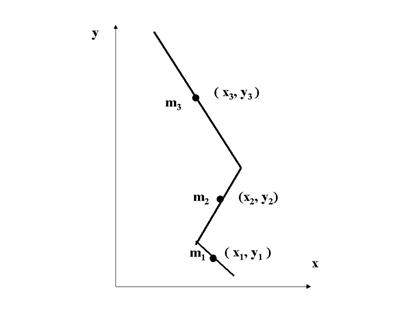
Sa consideram o masa distribuita pe un segment, ca in fig. 5. Momentul de inertie in jurul capatului sting al segmentului va fi :
I = ![]() [7]
[7]
Se poate vedea ca masa apropiata de centrul de masa are o influenta foarte mica asupra momentului de inertie I, in timp ce masa cea mai indepartata are un efect considerabil.
Masa unui volant este concentrata la periferia rotii avind o raza cit mai mare posibil. Momentul sau mare de inertie se va opune schimbarilor in viteza si prin aceasta tinde sa pastreze echipamentul in care este inclus la o viteza constanta.
Se considera, conform fig.5, o masa M care a fost divizata in doua puncte de mase egale, pentru care momentul de inertie calculat in raport cu centrul de masa este dat de expresia:
I0
= m![]() [8]
[8]
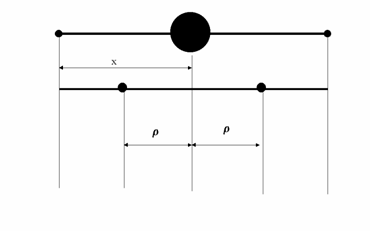
in care : r = raza de giratie, reprezentind o
distanta astfel aleasa incit momentul de inertie in planul de rotatie, al celor
doua mase egale sa fie egal cu cel al segmentului initial in raport cu centrul
de masa.
Fig.5
Se observa ca centrul de masa a acestor doua mase punctuale este inca acelasi cu cel al masei initiale distribuite.
TEOREMA AXELOR PARALELE
Majoritatea segmentelor corpuli nu se rotesc in jurul centrului lor de masa ci mai de graba in jurul articulatiei amplasate la unul dintre capete.
Masuratori in vivo ale momentului de inertie pot fi facute doar in raport cu centrul unei articulatii.Relatia dintre acest moment de inertie si cel in jurul centrului de masa este data de teorema axelor paralele.
O demonstratie a acestei teoreme este urmatoarea:
I = ![]() [9]
[9]
in care : I0 = momentul de inertie in jurul centrului de masa;
x = distanta dintre centrul de masa si centrul de rotatie;
m = masa segmentului
De fapt x poate fi orice distanta de pe oricare directie fata de centrul de masa atita timp cit este de-a lungul aceleiasi axe pentru care a fost calculat I0.
Momentul de inertie fata de centrul de masa este:
I0
= m![]()
![]() =
=
Momentul de inertie in raport cu articulatia genunchiului va fi:
I = I0
+ m.x2 = 0.06 + 3.(0.2)2 =
b. Daca distanta dintre
articulatia genunchiului si articulatia coapsei este de
Notind cu x = distanta de la centrul de masa la coapsa se obtine:
x = 20
+ 42 =
Momentul de inertie in raport cu articulatia soldului va fi :
Is
= I0 + m.x2 = 0.06 + 3.(0.62)2 =
Se observa ca in acest caz momentul de inertie este de aproximativ 20 de ori mai mare decit momentul de inertie in raport cu centrul de masa.
1.3.7 UTILIZAREA DATELOR ANTROPOMETRICE SI A DATELOR CINEMATICE
Utilizarea tabelului 1 si a datelor cinematice permite determinarea multor variabile necesare analizelor privind energia cinetica.
In acest tabel masa segmentelor este data ca procent din masa corpului iar centrele de masa ca procent din lungimile lor fata de capatul proximal sau distal.
Raza de giratie este de asemenea exprimata ca fractiune din lungimea segmentului, in raport cu centrul de masa, de capatul proximal si de cel distal.
1.3.7.1 Calculul maselor segmentelor si a centrelor lor de masa
Considerind un subiect
avind masa de
Lp =
Utilizind fractiunile de masa prezentate in tabelul 1, corespunzator fiecarui segment corporal,
se obtine:
mp = 0.0145 .80 =
mg = 0.0465 . 80 =
mc = 0.1
. 80 =
mCTB = 0.678 . 80 = 54.24
CMp = 0.5 ![]() m intre glezna si metatarsiene;
m intre glezna si metatarsiene;
CMg = 0.433![]() m sub condilul femural;
m sub condilul femural;
CMs =0.433![]() m sub marele trohanter;
m sub marele trohanter;
CMCTB= 1.142![]() m deasupra marelui trohanter
m deasupra marelui trohanter
.1.3.7.2 Calculul centrului de masa a intregului corp
in care : m1 + m2 + .+mn = M, reprezinta masa totala a sistemului de segmente.
Masele segmentelor individuale mI se determina pe baza procentelor fi in tabelul 1 ca fiind:
m1 = f1.M, m2 = f2.M. mn = fn .M
de unde rezulta :
x = ![]() [10]
[10]
Aceasta ecuatie este mai usor de utilizat pentru ca necesita doar cunoasterea fractiunii din masa totala si coordonatele centrului de masa pentru fiecare segment. Aceste fractiuni sunt date in tabelul 1.
Nu este intotdeauna posibil sa se masoare centrul de masa al fiecarui segment, mai ales daca nu se afla in cimpul vizual al echipamentului de inregistrare a miscarii.
1.3.7.3 Calcularea momentului de inertie
Pentru un subiect avind masa de
Din tabelul 1 rezulta pentru masa mg a gambei valoarea:
mg
= 0.0465 . 80 =
Lungimea gambei se determina pe baza datelor furnizate de fig.1:
Lg = 0.285H -
0.039H = 0.246H = 0.246 . 1.76 =
Raza de giratie se calculeaza pe baza rapoartelor prezentate in tabelul 1 :
![]()
![]()
![]()
![]()
Momentele de inertie fata de centrul de masa, capatul proximal si cel distal vor fi:
I = M ![]() = 3.72.(0.435 x 0.302)2 =
= 3.72.(0.435 x 0.302)2 =
Ip =![]() M (
M ( 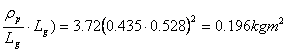
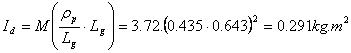
![]()
Se observa ca momentele de inertie fata de capatul distal sau proximal ar putea fi calculate si folosind teorema axelor paralele.
De exemplu, distanta centrului de masa al gambei fata de capatul proximal este:
x= 0.433 x 0.435 =
iar pentru momentul de inertie rezulta valoarea :
Ip = I0 + m.x2 = +
0.064 + 3.72 .( 0.188)2 =
Sa se calculeze momentul
de inertie a ansamblului cap-brate-trunchi (HAT) fata de capatul sa proximal si
fata de centrul sau de masa. Masa subiectului este de
Din tabelul cu date antropometrice se obtine:
mHAT= 0.678![]() ; lHAT=
; lHAT=
![]() ;
; ![]()
Deci :
Ip
= mHAT( ![]()
I0 = Ip - m.x2 = 10 - 52.54(0.295 x1.142)2 = 3.84 kgm2
In calcul s-ar putea
utiliza si raportul ![]() =0.903 obtinindu-se:
=0.903 obtinindu-se:
I0 = m![]()
1.4 MASURATORI EXPERIMENTALE
DETERMINAREA POZITIEI CENTRULUI DE MASA ANATOMIC AL
INTREGULUI CORP
Centrul de masa al intregului corp, numit si centru anatomic de masa, este usor de masurat cu ajutorul unei instalatii ( fig. 6) constind dintr-o placa basculanta montata la un capat pe un cintar iar la celalalt capat pe un element de spijin.
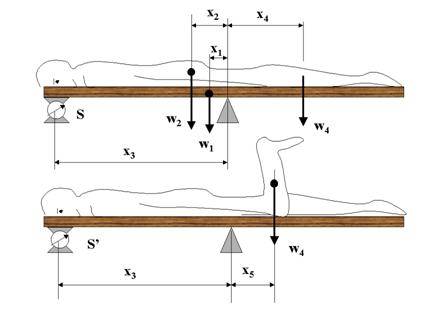
Punctul de spijin trebuie ales astfel incit centrul de greutate sa fie plasat intre acesta si cintar, de preferinta cit mai aproape de punctul de spijin. Prin respectarea acestei conditii se asigura o mai mare precizie masuratorilor prin posibilitatea utilizarii unor sisteme de cintarire cu o limita de masurare de (0-5) kg in loc de (50-100) kg.
Determinarea pozitiei centrului de greutate pentru intregul corp se realizeaza cu subiectul amplasat pe placa basculanta cu fata in jos.
w1 x1 +w2x2 = Sx3
de unde rezultata pentru pozitia centrului de masa valoarea data de expresia:
x2
=![]()
1.4.2 DETERMINAREA MASEI UNUI SEGMENT DISTAL
Masa sau greutatea unui segment distal poate fi determinata prin tehnica demonstrata anterior, in fig.6b. Segmentul al carui masa se doreste a fi determinata - de exemplu gamba si laba piciorului - este ridicat in pozitie verticala astfel incit pozitia centrului sau de masa sa fie deasupra centrului articulatiei.
Anterior ridicarii pozitia centrului de masa a segmentului este w4 iar indicatia cintarului in acest caz este S. Dupa ridicare centrul de masa va fi plasat la o distanta w5 de punctul de sprijin al placii basculante, indicatia cintarului fiind in acest caz S'.
Tinind cont ca descresterea in moment in sensul acelor de ceas, datorita miscarii segmentului este egala cu cresterea in momentul fortei de reactie a cintarului in raport cu punctul de sprijin, se poate scrie:
![]()
de unde rezulta pentru masa segmentului distal expresia:
![]()
Eroarea majora in aceasta determinare este data de eroarea in valoarea pozitiei x4 , a centrului de masa pentru segment, valoare care in mod obisnuit este obtinuta din tabele antropometrice.
Pentru a obtine masa intregului picior, acest experiment poate fi repetat cu subiectul asezat pe spate si cu piciorul flexat la 900. Din masa intregului picior se poate acum scadea cea a gambei si labei piciorului pentru a obtine masa coapsei.
DETERMINAREA MOMENTULUI DE INERTIE AL UNUI SEGMENT DISTAL
Pentru miscarea de rotatie, momentul de inertie reprezinta constanta de proportinalitate dintre acceleratia unghiulara a si momentul M carea a determinat aparitia acestei acceleratii, comform relatie:
M=I. a ( )
Aceasta ecuatie poate fi utilizata pentru determinarea momentului de inertie al unui segment distal, momentul fiind luat in raport cu articulatia proximala iar segmentul proximal fiind considerat fiaxat.
Pentru calculul direct al momentului de inertie se poate utiliza asa numita metoda a "eliberarii rapide"( fig.7). Pacientul amplasat pe un scaun are glezna prinsa intr-un mecanism de decuplare rapida care se opune fortei F, exercitate pe un cablu de tractiune la distanta y1 fata de articulatia genunchiului.
Pentru masurarea acceleratiei se utilizeaza un accelerometru ce este amplasat pe calcii la distanta y2 de genunchi. In pozitie neutra, sub actiunea fortelor ce actioneaza asupra lui, piciorul se va afla in echilibru.
Intre acceleratia tangentiala a, masurata de accelerometru, si cea unghiulara a exista relatia:
a = y2 . a
In momentul actionarii mecanismului de decuplare acesta va elibera brusc piciorul, forta de retinere a piciorului va scadea brusc la zero iar momentul net ce actioneaza pe picior va fi :
M = F.y1
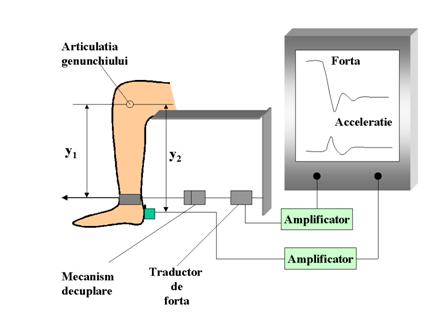
Avind in vedere
timpul scurt de desafasurare a evenimentului, pentru inregistrarea fortei F si
acceleratiei tangentiale a se poate utiliza un osciloscop cu memorie dubla.
Fig.7
Momentul de inertie pentru segmentul distal se va otine ca fiind:
![]()
Pe osciloscop se poate observa cresterea brusca a acceleratiei simultan cu descresterea rapida a fortie F ce actiona asupra piciorului.
Scaderea fortei este determinata de deplasarea inainte a piciorului ca urmare a actionarii mecanismului de decuplarea. Decuplarea poate avea loc, de exemplu prin taierea brusca a cablului ce retine piciorul.
Variatia brusca a acceleratiei poate fi utilizata pentru declansarea balaiejului de catre osciloscop, astfel incit sa se poata capta variatiile rapide ale fortei si acceleratiei.
In prezent exista echipamente sofisticate ce permit determinarea simultana a mai multor parametrii.
Astfel de tehnici au fost dezvoltate de Hatze (1975) si permit masurarea simultana a momentului de inertie, a pozitiei centrului de masa si a coeficientrului de amortizare
CENTRELOR DE ROTATIE ALE ARTICULATIILOR
Marker-ii atasati de corp sunt plasati, de obicei, pentru a reprezenta cele mai bune estimari ale centrelor articulatiilor.Totusi, datorita constringerilor anatomice, pozitionarile pot fi eronate.
Maleola laterala, de exemplu, este o localizare obisnuita pentru marker-ii articulatiei gleznei. Articularea suprafetelor tibie-talus se realizeaza, insa, astfel incit capatul distal al tibiei ( si fibula) sa se miste pe un arc de cerc peste talus. Adevaratul centru de rotatie este, de fapt, cu citiva centimetrii distal fata de maleola laterala.
La alte articulatii apar diferente si mai evidente. Articulatia soldului este deseori identificata in plan sagital printr-un marker plasat pe marginea superioara a marelui trohanter. Markerul este, in mod evident, plasat intrucitva mai lateral decit centrul articulatiei soldului astefel incit rotatiile interna si externa ale soldului relativ la pelvis, precum si abductia-aductia sa, pot cauza erori considerabile la nivelul soldului.
Apare astfel important a se identifica adevaratele centre de rotatie in raport cu markerii anatomici care sunt amplasati pe piele.
Pentru rezolvarea acestei probleme s-au dezvoltat mai multe tehnici care permit calcularea centrului instantaneu de rotatie al oricarei articulatii utilizind pentru aceasta istoricul deplasarii markeri-lor de pe doua segmente adiacente.
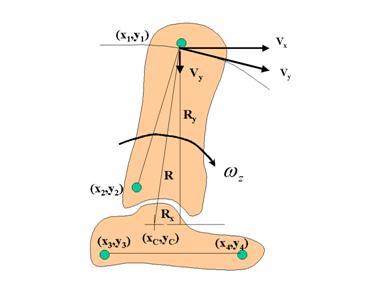
In figura 8 sunt prezentate doua astfel de segmente aflate in miscare
plana. Ele sunt translatate si rotite in spatiu astfel incit un segment sa fie
fix in spatiu iar cel de-al doile sa se roteasca dupa cum este indicat pe
figura.
Centrul de rotatie corespunzator unui moment oarecare de timp este ( xC , yC) el fiind amplasat in interiorul segmentului fixat. Ceea ce intereseaza este pozitia punctului ( xC , yC) relativ l a coordonatele anatomice (x3 , y3) si ( x4 , y4) ale segmentului.
Markerii (x1
,y1) si (x2,y2) sunt localizati ca in figura.
Marker-ul (x1,y1) are viteze tangentiala instantanee ![]() si este amplasat la raza R de centrul de rotatie.
Dreapta ce uneste punctele (x1,y1) si (x2,y2)
permite determinarea vitezei unghiulare
si este amplasat la raza R de centrul de rotatie.
Dreapta ce uneste punctele (x1,y1) si (x2,y2)
permite determinarea vitezei unghiulare ![]() a segmentului ce se roteste. Cu unul din segmente
fixat in spatiu,
a segmentului ce se roteste. Cu unul din segmente
fixat in spatiu, ![]() devine
viteza unghiulara a articulatiei, deci:
devine
viteza unghiulara a articulatiei, deci:
![]()
sau, in coordonate carteziene:
![]()
Deci:
![]() si
si ![]()
Avind in vedere ca Vx
, Vy si ![]() pot fi
calculate din informatiile privind traiectoria marker-ului, rezulta ca valorile
pentru Ry si Rz pot fi determinate. Pe baza pozitiei cunoscute
a markerului amplasat in (x1,y1) se va putea determina
pozitia (xC,yC) a centrului de rotatie al articulatiei. O
atentie deosebita trebuie acordata situatiilor corespunzatoare apropierii de
zero sau al schimbarii semnului( polaritatii) vitezei unghiulare
pot fi
calculate din informatiile privind traiectoria marker-ului, rezulta ca valorile
pentru Ry si Rz pot fi determinate. Pe baza pozitiei cunoscute
a markerului amplasat in (x1,y1) se va putea determina
pozitia (xC,yC) a centrului de rotatie al articulatiei. O
atentie deosebita trebuie acordata situatiilor corespunzatoare apropierii de
zero sau al schimbarii semnului( polaritatii) vitezei unghiulare ![]() , pentru ca in acest caz valorile pentru R
calculate cu relatiile de mai sus devin nedeterminate sau in mod eronat devin
foarte mari.
, pentru ca in acest caz valorile pentru R
calculate cu relatiile de mai sus devin nedeterminate sau in mod eronat devin
foarte mari.
ANTROPOMETRIA MUSCHILOR
Inainte de a putea calcula fortele produse de muschii individuali in timpul miscarii normale, este in mod obisnuit necesara cunoasterea citorva dimensiuni chiar de la muschi.
Daca muschii aceluiasi grup imart sarcina, aceasta are loc probabil proportional cu sectiunile lor transversale. De asemenea lucrul mecanic al fiecarui muschi poate fi diferit in functie de lungimea bratului de actiune al fortei in raport cu originea si insertia muschiului si in functie de alte structuri de sub muschi sau tendoane, care altereaza unghiul de actiune al tendonului.
ARIA TRANSVERSALA A MUSCHILOR
Aria transversala functionala sau fiziologica (PCA) a muschilor este o masura a numarului de sarcomeri in paralel cu unghiul de tragere al acestora. In muschii penati fibrele actioneaza la un unghi fata de axa longitudinala si de aceea nu sunt tot atit de eficient ca muschii cu fibrele dispuse in paralel.
Unghiul dintre axa longitudinala a muschiului si axa fibrei este numit "unghi de penatie".
In muschii cu fibrele dispuse in paralel, aria transversala (PCA) este data de relatia:
![]() [cm2]
[cm2]
in care: m = masa fibrelor musculare [g];
d = densitatea muschiului [g/cm3] = 1.056 g/cm3;
l = lungimea muschiului [cm].
In muschii penati aria transversala (PCA) devine:
![]() [cm2]
[cm2]
in care q = unghiul de penatie, care creste cu scurtarea muchiului.
Wichiewicz si colaboratorii (1983) au folosit datele prelevate de la trei cadavre si au masurat masa , lungimile fibrelor si unghiul de penatie pentru 27 de muschi ai membrului inferior. Valorile reprezentative sunt date in tabelul . Aria transversala (PCA), ca procent din aria totala a tuturor muschilor ce traverseaza o articulatie data este prezentata in tabelul .
Se poate determina astfel contributia potentiala relativa a unui grup de muschi agonisti, presupunind ca fiecare genereaza aceeasi solicitare. Trebuie observat ca un muschi dublu articular, ca de exemplu gastronemius, poate prezenta procente diferite la articulatii diferite datorita ariei transversale totale (PCA) diferita a tuturor muschilor ce traverseaza articulatia.
MODIFICAREA LUNGIMII MUSCHIULUI IN TIMPUL MISCARII
Putine studii au investigat modificarile in lungime a muschilor ca functie de unghiurile articulatiilor ce le traverseaza.
Grieve si colaboratorii
(1978) au raportat intr-un studiu efectuat pe 8 cadavre modificarile
procentuale in lungime ale muschiului gastrinemius ca functie de unghiul
genunchiului si gleznei. Lungimea de repaus a muschiului gastrocs s-a presupus
a fi in pozitia flexata cu
1.5.3 FORTA PE UNITATE DE SUPRAFATA TRANSVERSALA (TENSIUNEA)
Au fost raportata o gama larga de valori pentru tensiuni ale muschilor scheletici (Haxton-1944, Alexander si Vernon - 1975,Maughan si colaboratorii -1983).
Majoritatea acestor valori de tensiune au fost masurate in conditii izometrice si erau intre 20 -100N/cm2. Valorile mai mari au fost obtinute in muschii penati care sunt cei ale caror fibre sunt dispuse sub un unghi fata de axa muschiului. O astfel de orientare creste efectiv aria transversala peste cea masurata si folosita in calcularea tensiunii.
Haxton (1944) a stabilit legatura dintre forta si tensiune in doi muschi penati ( gastrocs si soleus) si a gasit valori de 38N/cm2. Tensiunile dinamice au fost calculate in cvadricepsi in timpul alergarii si sariturilor si s-a obtinut 70N/cm2 ( pe baza unui moment extensor maxim la genunchi de 210 Nm, pentru barbat adulti) si ~100N/cm2 in MVC izometrica ( Maughan si colaboratorii, 1983)
LUCRUL MECANIC MUSCULAR
Originea si insertia fiecarui muschi defineste unghiul de tragere a tendonului pe os si prin aceasta pirghia mecanica a acestuia fata de centrul articulatiei.
Fiecare muschi are o lungime a bratului de forta unica, care este lungimea liniei normale pe muschi, trecind prin centrul articulatiei. Acest brat se modifica ca lungime in functie de unghiul articulatiei.
Unul dintre putinele studii in acest domeniu (Smidt,1973) comunica lungimea medie a bratului de forta ( pentru 26 de subiecti) pentru muschii extensori ai genunchiului si pentru hamstringsi, ce actioneaza la genunchi. Ambele grupe de muschi au aratat o crestere in lungime a bratului de forta in timpul flexiei genunchiului, atingind un maxim la 450 si descrescind apo cind flexia creste la 900.
Wilkie (195) a realizat de asemenea cercetari privind momentele si lungimile pentru flexorii cotului.
MUSCHI MULTIARTICULARI
Un numar mare de muschi din corpul uman trec peste mai mult de o articulatie. In membrele inferioare muschii hamstring sunt extensori ai coapsei si flexori ai genunchiului, rectus femoris este o combinatie de flexor al coapsei si extensor al genunchiului iar gastronemius sunt flexori ai genunchiului si plantarflexori pentru glezna.
Lungimile fibrelor multora dintre acesti muschi pot fi insuficiente pentru a permite o gama completa de miscae pentru ambele articulatii implicate. Sa consideram, de exemplu, actiunea lui rectus femoris in timpul fazei timpurii de balans din alergare. Acest muschi se scurteaza ca rezultat al flexiei coapsei si se lungeste la genunchi in balansul inapoi al piciorului ce se pregateste de balans. Tensiunea din rectus femoris creaza un moment de flexie a coapsei ( lucru mecanic pozitiv) si un moment de extensie a genunchiului pentru a decelera laba piciorului in balans( lucru mecanic negativ) si incepe accelerarea lui inainte. In acest fel modificarea neta in lungimea muschiului este redusa in comparatie cu doi muschi uniarticulari echivalenti, iar lucrul mecanic pozitiv si negativ din muschi poate fi redus.
Un muschi biarticular poate fi chiar total izometric in astfel de situatii si ar putea efectiv sa transmita energie de la picior catre pelvis in exemplul de mai sus. In alergare in timpul fazei critice de propulsie (push-off), cind plantarflexorii genereaza energie cu o viteza mare, genunchiul continua sa se extinda. Astfel, muschii gastronemius pot actiona esential izometric( apar a se scurta la capatul distal si a se lungi la cel proximal). In mod similar, catre sfirsitul balansului in alergare, genunchiul este rapid extins, in timp ce coapsa a atins flexia totala si incepe miscarea inversa ( adica ea are o viteza de extensie). In acest fel muschii hamstrings apar a fi lungiti rapid la capatul distal si scurtati la cel proximal, cu un rezultat net de a se putea lungi la viteza mai scazuta decit ar face-o o articulatie unica.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4655
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved