| CATEGORII DOCUMENTE |
| Animale | Arta cultura | Divertisment | Film | Jurnalism | Muzica |
| Pescuit | Pictura | Versuri |
Distributia multinomiala - Testele chi-patrat
Distributia multinomiala
Evenimentele de tip binomial se caracterizeaza prin caracterul dihotomic, putand lua doar doua valori. Exista insa si evenimente care pot lua mai mult de doua valori posibile (trei sau mai multe). De exemplu, daca presupunem ca exista doar trei tipuri de liceu, atunci absolventii de liceu, ar putea face parte dintr-una din urmatoarele categorii: "umanist", "real", "artistic". Daca raportam frecventa de aparitie a fiecarei categorii (numarul subiectilor care au absolvit un anumit tip de liceu) la totalul subiectilor, probabilitatile aferente fiecarui tip de liceu sunt, respectiv, P, Q si R. Intr-o asemenea situatie P+Q+R=1. Pe aceasta baza, putem scrie probabilitatile pentru fiecare "eveniment" dupa modelul: Q=1-P-R.
Sa luam in considerare situatia in care toate liceele ar avea acelasi numar de absolventi. In acest caz, P=Q=R=1/3=0.33 (alegerea unor ponderi diferite, asa cum este si cazul in realitate, nu ar schimba datele rationamentului care urmeaza, dar l-ar face mai putin evident). Mai departe, sa ne imaginam ca analizam tipul de liceu absolvit de studentii unei facultati de psihologie si constatam ca din 100 de studenti 60 sunt absolventi de liceu "umanist", 30 au absolvit un liceu cu profil "artistic" si 10, unul cu profil "real". Ponderea studentilor la facultatea respectiva este, evident, diferita de ponderea din cadrul populatiei de absolventi. Pe baza acestor date, se poate afirma ca absolventii de profil "umanist" si "artistic" prefera psihologia mai mult decat care au absolvit un profil "real"? Sau, intr-o formulare mai larga, se poate afirma ca exista o relatie intre tipul de liceu absolvit si preferinta pentru psihologie ca specialitate universitara?
Inainte de a raspunde la aceasta intrebare, sa analizam putin datele sugerate de exemplul de mai sus. Asa cum am spus, numarul studentilor la facultatea de psihologie este, in functie de tipul de liceu absolvit, de 60, 30, respectiv, 10. Aceste valori se numesc "frecvente observate" sau "frecvente calculate" (notate cu fo de la Observed), fiind rezultatul masurarii in contextul cercetarii. Daca preferinta pentru facultatea de psihologie nu ar fi in legatura cu liceul absolvit (ipoteza de nul), atunci cercetarea ar trebui sa consemneze un numar egal de studenti provenind din fiecare tip de liceu. In exemplul dat, acest numar ar trebui sa fie, pentru fiecare tip de liceu 100/3=33.3, care se numeste "frecventa teoretica" sau "frecventa asteptata" (notata cu fe de la Expected). Este usor de intuit faptul ca, cu cat frecventele calculate (reale) sunt mai indepartate de cele asteptate (teoretice), cu atat ele se apropie de situatia de a fi "semnificativ diferite" de acestea. Mai departe, nu ne ramane decat sa gasim o procedura pentru calcularea distantei dintre cele doua tipuri de frecvente si un model de distributie pentru rezultatul acestui calcul, in raport cu care sa putem lua o decizie cu privire la ipoteza de nul.
Datele din exemplul dat nu mai pot fi analizate prin prisma distributiei binomiale deoarece implica mai mult decat doua "evenimente" posibile. De aceea, distributia acestora se numeste "distributie multinomiala". Desigur, procedura de calcul pentru acest caz ar putea urma modelul celei binomiale dar, din cauza complexitatii acestei solutii, s-a apelat la o solutie mai simpla. Aceasta este fundamentata pe o aproximare derivata din formula binomiala a lui z, care este pur si simplu ridicata la patrat, devenind:
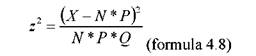
Daca inainte de ridicarea la patrat z urmeaza o distributie normala, dupa ridicarea la patrat z urmeaza un alt tip de distributie, numita "chi-patrat", simbolizata cu litera greceasca χ, cu indicele de ridicare la patrat (χ2). Valorile distributiei χ2 se calculeaza ca raport dintre frecventele observate si cele teoretice, iar caracteristicile ei esentiale sunt urmatoarele;
. este, la fel ca distributia normala, o familie de distributii;
. are forma asimetrica;
. are originea in zero (din cauza ridicarii la patrat);
. are o forma dependenta de numarul de grade de libertate.
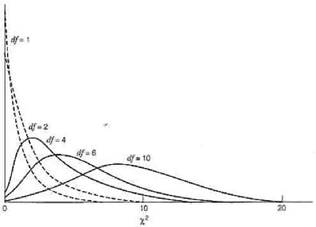
Imaginea de mai jos prezinta mai multe distributii chi-patrat, pentru diferite grade de libertate (vom vedea mai tarziu cum se calculeaza acestea).
Curbele distributiilor chi-patrat pentru 1, 2, 4, 6 si 10 grade de libertate
Tabelul de corespondenta (contingenta) pentru date nominale
Inainte de a trece la testul propriu-zis, este util sa aruncam o privirea asupra modului de organizare a datelor pentru o situatie similara exemplului de mai sus. In acest scop, putem sa ne permitem o largire a cadrului de investigare. Sa presupunem ca avem cele trei categorii de liceu si ne intereseaza distribuirea lor, nu in legatura cu o singura facultate (cea de psihologie), ci in legatura cu trei tipuri de facultati: "umaniste", "artistice" si "tehnice".
Daca realizam un cadru de reprezentare sintetic al valorilor celor doua variabile, obtinem ceea ce se numeste un tabel de corespondenta. Iata cum ar arata un astfel de tabel, pentru un set de date ipotetice:
|
|
Liceu umanist |
Liceu real |
Liceu artistic |
Total pe linii |
|
Fac. Umaniste |
45 |
20 |
30 |
95 |
|
Fac. Tehnice |
14 |
60 |
12 |
86 |
|
Fac. Artistice |
20 |
13 |
50 |
83 |
|
Total pe coloane |
79 |
93 |
92 |
264 |
Acesta este un tabel de corespondenta pentru doua variabile nominale, fiecare avand cate trei valori distincte (categorii)1. Valorile din celule reprezinta numarul de cazuri (frecventele observate) care corespund fiecarei combinatii dintre categoriile celor doua variabile. "Totalul pe linii" exprima numarul de studenti din fiecare facultate, consemnati in
1 In mod similar, se pot crea tabele de corespondenta pentru variabile categoriale avand, fiecare, un numar diferit de valori (categorii).
cercetare, indiferent de tipul de liceu absolvit, "totalul pe coloane", exprima numarul de absolventi din fiecare tip de liceu, indiferent de facultatea la care sunt inscrisi, iar la intersectia celor doua totaluri regasim totalul general al subiectilor cercetarii (N=264).
Fundamentarea testului statistic
Avand un numar de 95 de studenti in "facultati umaniste", aceasta inseamna ca ei reprezinta 36% din totalul subiectilor cercetarii (95/264*100=36). Acest procent indica se refera la absolventii care au ales o facultate de tip umanist, indiferent de liceul absolvit. In mod similar, calculam procentele corespunzatoare celorlalte tipuri de facultati. Valorile astfel calculate, pentru fiecare linie a tabelului, se numesc frecvente marginale.
Daca alegerea facultatii nu ar avea nici o legatura cu tipul de liceu absolvit atunci, in mod normal, ar trebui sa regasim, pentru fiecare tip de liceu, acelasi procent care exprima ponderea studentilor din fiecare facultate in totalul subiectilor cercetati. Avand procentele studentilor din fiecare facultate si numarul absolventilor din fiecare tip de liceu, putem calcula frecventele "teoretice" (asteptate) pentru fiecare celula a tabelului. De exemplu, dintre cei 79 de absolventi de liceu umanist consemnati de cercetare, 36% ar trebui sa se afle in facultati umaniste, ceea ce inseamna: (79*36)/100=28.4. In mod similar, ar trebui sa avem 32.5% (25.6) in facultati stiintifice si 31.5% (24.8) in facultati artistice. Acelasi rationament se aplica mai departe si celorlalte tipuri de liceu, cu utilizarea procentului corespunzator fiecarei facultati. Precizam ca frecventele teoretice (asteptate) vor fi aceleasi, in fiecare celula, chiar daca vor fi calculate pe baza frecventelor marginale de pe coloane.
|
|
Liceu umanist |
Liceu real |
Liceu artistic |
Total pe linie |
% pe linii |
|
Fac. Umaniste |
45 (28.4) |
20 (33.4) |
30 (33.1) |
95 |
(95/264)* 100=36% |
|
Fac. Tehnice |
14 (25.6) |
60 (30.2) |
12 (29.9) |
86 |
(86/264)* 100=32,5% |
|
Fac. Artistice |
20 (24.8) |
13 (29.2) |
50 (28.9) |
83 |
(83/264)* 100=31.5% |
|
Total pe coloana |
79 |
93 |
92 |
264 |
|
Asa cum constatam, intre frecventele observate si cele asteptate sunt diferente. Suma frecventelor asteptate (teoretice) este egala cu suma frecventelor observate (poate rezulta o anumita diferenta intre totaluri, ca urmare a aproximarii zecimalelor).
In final, problema cercetatorului este aceea de a stabili daca intre frecventele observate si cele teoretice (calculate) este o diferenta care sa justifice aprecierea ca intre cele doua variabile exista sau nu o legatura. Datele de acest gen nu mai pot fi analizate prin prisma distributiei binomiale, deoarece implica mai mult decat doua "evenimente" posibile. De aceea, distributia acestora se numeste "distributie multinomiala". Desigur procedura de calcul pentru acest caz ar putea urma modelul celei binomiale dar, din cauza complexitatii ei, s-a apelat la o solutie mai simpla. Aceasta solutie este fundamentata pe o aproximare derivata din formula binomiala a lui z, care este pur si simplu ridicata la patrat, devenind:
z2 (X-N*P)2
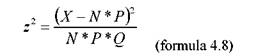
|
Daca inainte de ridicarea la patrat z urmeaza o distributie normala, dupa ridicarea la patrat z urmeaza un alt tip de distributie, numita "chi-patrat", simbolizata cu litera greceasca χ cu indicele de ridicare la patrat (χ2). Fara a intra in amanunte, vom preciza ca distributia χ2 prezinta urmatoarele caracteristici: |
. este, la fel ca si distributia normala, o familie de distributii;
. are forma asimetrica;
. are originea in zero (din cauza ridicarii la patrat);
. are o forma dependenta de numarul de grade de libertate.
La fel ca si distributiile t si F, distributia χ2 este dependenta de numarul gradelor de libertate. Acestea se calculeaza pe baza tabelului de corespondenta dintre cele doua variabile, astfel:
df=(numar coloane-1)*(numar linii-1)
Formula de calcul pentru testul chi-patrat, derivata din formula 4.8, este :
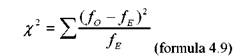
unde fO este frecventa observata, iar fE, frecventa asteptata.
Decizia pentru testul chi-patrat se bazeaza pe compararea valorii calculate cu o valoare critica, corespunzatoare nivelului alfa ales (0.05 sau, optional, mai mic). Valorile critice pentru distributia chi-patrat se gasesc intr-o tabela speciala (vezi anexa). Daca valoarea calculata a lui χ2 este egala sau mai mare decat valoarea critica pentru nivelul ales al lui alfa, atunci ipoteza de nul poate fi respinsa, iar ipoteza cercetarii confirmata.
Pe aceasta structura formala se bazeaza doua variante distincte ale testului chi-patrat: testul corespondentei (Goodness of Fit) si testul asocierii. Primul, compara frecventele observate ale valorilor unei singure variabile cu frecventele asteptate pentru acele valori. Al doilea, compara frecventele valorilor observate pentru doua variabile cu frecventele lor asteptate, cu scopul de a testa relatia (asocierea) dintre cele doua variabile.
Chi-patrat pentru gradul de corespondenta (Goodness of Fit)
Aceasta varianta a testului chi-patrat compara frecventele observate ale unei distributii cu frecventele teoretice (asteptate) ale acelei variabile. De exemplu, daca avem frecventele unei variabile putem afla daca aceasta se distribuie dupa curba normala (z), prin compararea cu frecventele cunoscute ale acestei distributii (aria de sub curba).
Sa presupunem ca a fost aplicat un test de cunostinte unui esantion de 200 de elevi, care a fost evaluat cu calificative, astfel: F.Slab, Slab, Mediu, Bun, F.Bun.
Problema cercetarii: Calificativele obtinute se distribuie normal la nivelul clasei?
Populatia 1: Calificativele obtinute de elevi.
Populatia 2: Calificativele, asa cum s-ar distribui pe o curba normala: FS=2.5%,
B=14%, M=67%, B=14% si FB=2.5% (procentele sunt cele tipice unei curbe z, impartite in cinci clase valorice).
. Ipoteza cercetarii (H1): Distributia calificativelor urmeaza legea curbei normale la nivelul esantionului de elevi.
. Ipoteza de nul (H0): Distributia calificativelor nu urmeaza legea curbei normale in randul elevilor examinati.
Determinarea caracteristicilor deciziei statistice:
. alegem α=0.05 (in cazul testului χ2 decizia nu poate fi decat unilaterala, deoarece acest test nu poate lua valori negative)
. gasim valoarea critica pentru χ2=9.48 in tabela pentru distributia χ2, pentru df=(2-1)*(5-1)=4 si α=0.05
|
|
|
Tabelul urmator contine datele de cercetare si algoritmul de calcul: |
Decizia statistica:
. χ2 calculat (18,33) este mai mare decat χ2 critic (9,48)
. Respingem ipoteza de nul si tragem concluzia ca distributia calificativelor urmeaza forma curbei normale.
Concluzia statistica poate fi interpretata, in acest caz, ca fiind negativa din punctul de vedere al eficientei procesului didactic. In mod normal, daca activitatea de invatare ar fi eficienta, rezultatele elevilor ar trebui sa se distribuie asimetric negativ, adica cu tendinta de grupare a valorilor spre calificativele superioare. Rezultatele procesului de invatare nu se distribuie "normal", nefiind un proces "natural", ci unul in care valorile (calificativele) sunt supuse unei influente sistematice (prin efortul profesorilor si al elevilor insisi) inspre valorile mari.
Facem, inca o data, precizarea ca aceasta forma a testului chi-patrat se aplica atunci cand vrem sa comparam frecvente observate cu frecvente teoretice (asteptate), pe care le cunoastem deja. El este echivalentul testului z pentru proportii pentru distributia binomiala, cu specificatia ca se utilizeaza atunci cand avem mai mult de doua categorii. Testul chi-patrat pentru gradul de corespondenta (goodness of fit) nu are un indice de marime a efectului.
Iata cateva exemple posibile de cercetari ale caror date pot fi analizate cu testul chi-patrat al gradului de corespondenta:
. Vrem sa stim daca exista o preferinta pentru o anumita categorie de muzica (clasica, populara, pop-rock). In acest caz, daca distributia preferintelor nu ar fi influentata de nici o anumita preferinta (ipoteza de nul) atunci frecventa asteptata (teoretica) pentru fiecare gen muzical ar trebui sa fie echivalenta cu 100/3=33.3% numarul subiectilor. Mai departe, nu ne ramane decat sa testam diferenta dintre cele doua categorii de frecvente (teoretice si observate), conform modelului de calcul de mai sus.
. Intr-un studiu asupra relatiei dintre atractivitate si preferinta pentru profesori, unui numar de studenti li se prezinta fotografiile preselectate ale unor sase potentiali profesori, ale caror portrete sugereaza grade diferite de atractivitate, si li se cere sa aleaga dintre acestia pe cel pe care ar dori sa il aiba ca profesor. Daca gradul de atractivitate nu are
nici un impact asupra preferintei ca profesor, atunci frecventele cu care sunt alese fotografiile ar trebui sa fie egale (100/6=16.6%).
. Intr-un studiu de marketing, o companie trebuie sa aleaga dintre patru propuneri imagini. Acestea sunt prezentate unui esantion de subiecti si se consemneaza numarul de preferinte exprimate pentru fiecare imagine. Daca toate ar avea acelasi impact, atunci numarul de preferinte ar trebui sa fie egal (25%, pentru fiecare imagine).
Chi-patrat - testul asocierii (independence chi-square)2
Aceasta varianta a testului chi-patrat este mai frecvent utilizata. Ea compara frecventele observate ale unei distributii (variabile) cu frecventele corespondente ale altei distributii (variabile), ambele masurat pe scale de tip categorial, cu scopul de a vedea daca exista o asociere intre cele doua variabile.
Sa presupunem ca avem rezultatele la testul de statistica (masurate pe o scala ordinala si notate, conventional, cu A, B, C, D, E, unde A reprezinta nivelul de performanta cel mai ridicat iar E, cel mai scazut).
Problema cercetarii: Dorim sa aflam daca exista o diferenta semnificativa intre baieti (M) si fete (F) la testul de statistica.
Ipoteza cercetarii: Distributia performantei depinde de genul "masculin" sau "feminin".
Ipoteza de nul: Rezultatele la testul de statistica nu au legatura cu variabila sex.
Determinarea criteriilor de decizie statistica:
. alegem α=0.05
. df=(2-1)*(5-1)=4
. citim valoarea critica pentru χ2 in tabela pentru distributia χ2:
. χ2critic= 9.49
Datele cercetarii ar putea fi astfel centralizate in urmatorul tabel de corespondenta3:
|
|
A 10 10 20 Performanta la test |
|
||||
|
A
|
B |
C |
D |
F |
Total |
|
|
Masculin |
10 |
34 |
140 |
10 |
6 |
200 = 57.14% din total general |
|
Feminin |
10
|
32 |
97 |
6 |
5 |
150 = 42.86% din total general |
|
Total |
20
|
66 |
237 |
16 |
11 |
Total general=350 |
. Frecventele marginale sunt: 200 (57.14%) pentru "baieti" si 150 (42.86%) pentru "fete"
. Daca performanta la test nu are nici o legatura cu genul subiectilor, trebuie sa regasim aceste procente pentru fiecare dintre calificativele acordate.
. Aceasta inseamna ca, teoretic, in celula A/Masculin, ar trebui sa gasim, proportional, tot atatia baieti cati sunt pe intregul lot (57.14%). Adica (20*57.14)/100=11.42, care reprezinta frecventa asteptata pentru celula respectiva din tabelul de corespondenta.
. La fel, pentru celula A/Feminin ar trebui sa avem 42.86% din totalul pentru "feminin", adica: (20*42.86)/100=8.52.
. In acelasi mod de calculeaza frecventele observate pentru fiecare celula a tabelului.
2 Cunoscut si sub numele "testul chi-patrat Pearson al asocierii", a fost elaborat de Karl Pearson.
3 Datele din acest exemplu nu se refera la o situatie reala.
Pentru o mai usoara intelegere a mecanismului de calcul, vom rearanja tabelul astfel:
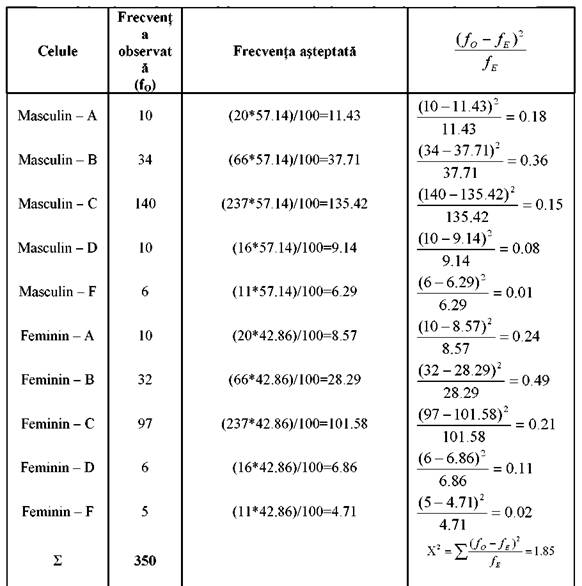
. Se compara χ2 critic (9.49) cu χ2 calculat (1.85) pentru df = (2-1)(5-1) = 4
. Valoarea calculata a testului este mai mica decat valoarea critica, ca urmare, acceptam ipoteza de nul. Rezultatele la test nu confirma ipoteza ca rezultatele se distribuie in functie de apartenenta de gen a subiectilor.
Conditii pentru aplicarea testului χ2
. Cele doua variabile nu trebuie sa se "intersecteze" (sa nu existe subiecti care sa fie inclusi in mai mult de o celula de tabel)
. Selectie aleatoare a esantioanelor
. Este recomandabil ca frecventa asteptata sa nu ia valori mai mici de 5 (sau, cel putin, in nu mai mult de 20% din celule).
. Nici o celula nu trebuie sa aiba frecventa asteptata mai mica de 1.
Pentru situatiile in care frecventele asteptate sunt mai mici decat specificatiile de mai sus, sau atunci cand tabelul de corespondenta dintre variabile are doua linii si doua coloane, se recomanda aplicarea unei corectii la formula de baza. Aceasta se numeste "corectia
|
|
|
Yeates" si consta in scaderea unei constante (0.5) din expresia de la numarator, luata in valoare absoluta: |
Utilizarea testului chi-patrat al asocierii
Testul chi-patrat al asocierii se utilizeaza atunci cand dorim sa testam relatia dintre doua variabile, ambele masurate pe scala de tip categorial. Facem precizarea ca variabilele categoriale desi sunt, de regula, de tip nominal, pot fi atat ordinale cat si de interval sau de raport. Ceea ce caracterizeaza o variabila categoriala nu este atat scala de masurare, cat faptul ca primeste putine valori, care impart distributia in categorii de valori. De exemplu, intr-un studiu cu privire la relatia dintre gravitatea accidentelor de circulatie ("fara raniti", "cu raniti usor", "cu raniti grav", "cu morti") si puterea motoarelor (1400 cm3, 1600 cm3, 2000 cm3, 2500 cm3, 3000 cm3), ambele variabile sunt de tip categorial, dar prima este pe scala nominala, iar a doua pe scala cantitativa.
Testul chi-patrat al asocierii (independentei) poate fi vazut ca un veritabil test de corelatie pentru date categoriale. De asemenea, poate fi folosit in locul testului t sau ANOVA, daca nu sunt indeplinite conditiile pentru variabila dependenta. Intr-un asemenea caz, variabila dependenta cantitativa se transforma, prin gruparea in frecvente, in variabila de tip categorial. Aceasta optiune se va alege numai daca ne aflam in fata unei flagrante violari a conditiei de normalitate, deoarece testele parametrice au o putere mai mica decat cele neparametrice. La fel ca si in cazul altor teste statistice, nu se vor putea trage concluzii de tip cauzal decat numai daca variabilele sunt masurate in contextul unui experiment psihologic.
Marimea efectului pentru testul chi patrat al asocierii
Coeficientul φ (fi)
Atunci cand utilizam testul pentru asocierea variabilelor, valoarea χ2 certifica faptul ca cele doua variabile sunt relationate. Dar marimea lui χ2 nu ne spune nimic cu privire la intensitatea relatiei dintre variabile. De fapt, marimea lui χ2 este in functie de N. Daca multiplicam frecventele celulelor cu o constanta, valoarea lui χ2 se multiplica si ea cu acea constanta, singura consecinta fiind aceea ca se diminueaza probabilitatea ca valoarea respectiva sa fie obtinuta din intamplare. Pentru completarea interpretarii valorii χ2 este necesar un indicator suplimentar, care sa ne spuna ceva si despre intensitatea legaturii, nu doar despre semnificatia acesteia. Un astfel de indicator este coeficientul φ (fi), care se calculeaza pentru asocierea variabilelor care prezinta fiecare doar doua valori posibile (tabele de contingenta 2x2).
Formula dupa care se calculeaza este:
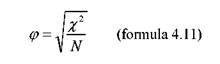
Coeficientul φ Cramer
Coeficientul φ este adecvat doar pentru tabelele de contingenta de tip 2x2, cand ambele variabile sunt dihotomice. O usoara modificare a acestuia, denumita φ Cramer, il face utilizabil pentru intensitatea asocierii dintre variabile avand un numar diferit de categorii.
|
|
|
Indicele φ Cramer se calculeaza dupa formula: |
unde:
. N este volumul esantionului
. L este valoarea cea mai mica dintre numarul liniilor sau al coloanelor tabelului de corespondenta (de exemplu, pentru un tabel de corespondenta 4x3 - patru linii si patru coloane - L are valoarea 3-1=2).
In cazul coeficientilor φ, daca frecventele fiecarei celule din tabelul de corespondenta sunt multiplicate cu o constanta, atat χ2 cat si N cresc concomitent, iar valoarea coeficientului φ ramane aceeasi. Coeficientul φ se modifica numai daca se modifica si raporturile dintre proportii, ceea ce inseamna ca marimea lui nu este influentata de N. El reprezinta un indicator numeric al intensitatii relatiei si poate lua valori intre zero - absenta relatiei si unu - relatie perfecta intre cele doua variabile. De exemplu, pentru testul chi-patrat al asocierii dintre gen si performanta la testul de statistica (care a rezultat nesemnificativ), al carui tabel de corespondenta este de forma 2x5, valoarea coeficientului φc este:
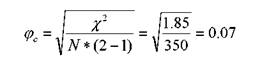
Interpretarea coeficientilor φ
Valoarea coeficientului φ se asociaza interpretarii testului chi-patrat, atunci cand acesta este semnificativ, pentru a adauga o informatie suplimentara cu privire la intensitatea relatiei. Prin ridicarea la patrat a expresiei de calcul, coeficientul φ2 poate fi interpretat procentual, la fel ca si coeficientul de determinare (r2), indicand proportia variatiei unei variabile determinata de variatia celeilalte variabile. In cazul nostru, numai 0.4% (0.072*100) din variatia calificativelor la testul de statistica este explicata prin diferenta de gen (masculin/feminin), ceea ce, in conformitate cu decizia statistica, s-a dovedit a fi nesemnificativ.
In conformitate cu recomandarile lui Cohen, cit. de Kotrlik si Williams (2003), valorile lui φ vor fi interpretate dupa cum urmeaza:
|
φ (Cohen) |
0.10 0.25 0.40 |
efect mic |
|
efect mediu |
||
|
efect mare |
Raportarea rezultatului
In cazul testului χ2 elementele care vor fi incluse in raport sunt urmatoarele: gradele de libertate, valoare testului, nivelul p si coeficientul φ sau Cramer φ. In varianta narativa, pentru exemplul de mai sus, prezentarea rezultatelor ar putea avea urmatoarea forma:
"Rezultatele testului de statistica, evaluate pe cinci clase valorice (A,B,C,D,E) au fost comparate pe sexe. Testul χ2 pentru asocierea variabilelor indica faptul ca rezultatele nu difera semnificativ in functie de gen, χ2(4) = 1.85, p >0 .05, cu un coeficient φ=0.07, care indica o asociere slaba".
In cazul in care testul ar fi fost semnificativ, raportarea rezultatelor ar fi trebuit sa contina si referinte cu privire la procentele consemnate in celulele tabelului de corespondenta, astfel incat sa fie scoase in evidenta diferentele releavnte dintre categoriile comparate.
Testul exact Fisher
Asa cum am precizat, testul chi-patrat este calculat pe baza unei formule ale carei rezultate nu urmeaza cu maxima precizie distributia χ2. Daca in cele mai multe situatii acest lucru nu reprezinta un neajuns notabil, sunt si cazuri in care rezultatele pot fi alterate suficient de mult pentru a putea fi luate in considerare:
. atunci cand volumul esantionului este redus (N<20);
. atunci cand valorile fe pentru una sau mai multe dintre celulele tabelei de corespondenta sunt foarte mici.
In aceste situatii, precum si atunci cand tabelul de corespondenta este compus din doua linii si doua coloane, este recomandabila utilizarea testului exact Fisher. El se bazeaza pe calcularea tuturor tabelelor posibile ce pot fi construite pentru frecventele marginale. Deoarece necesita un mare volum de calcule, testul exact Fisher se efectueaza numai cu ajutorul programelor computerizate.
Rezumat
. Distributia binomiala deriva din serii de evenimente independente dihotomice. Cele doua posibilitati ale fiecarui eveniment au probabilitatile P si Q, a caror suma este 1 (de unde Q=1-P).
. Atunci cand P=Q=0.5, distributia binomiala este simetrica. Pe masura ce numarul evenimentelor (N) creste, distributia binomiala se apropie de forma normala. Chiar si atunci cand P≠Q distributia binomiala se apropie de forma normala odata cu cresterea lui N.
. Atunci cand N creste la infinit, distributia binomiala devine normala, avand
media=N*P si abaterea standard=![]() Ca urmare, probabilitatea ca un
Ca urmare, probabilitatea ca un
anume eveniment sa cada in categoria P poate fi aproximata prin calcularea unui scor z si evaluarea ariei corespunzatoare de sub curba normala.
. Daca P=0.5, distributia normala devine o aproximare buna pentru distributia normala incepand cu N=25.
. Testul semnului poate fi utilizat in locul testului t pentru esantioane dependente atunci cand nivelul diferentei dintre cele doua determinari nu poate fi evaluat, ci numai directia diferentei. Dat fiind faptul ca fiecare diferenta poate fi intr-una din categorii (+ sau -) distributia binomiala poate fi utilizata pentru a estima in ce masura dezechilibrul intre cele doua categorii este posibil sa apara din intamplare (prin raportare la distributia normala).
. Atunci cand N nu este foarte mare, utilizarea distributiei normale pentru aproximarea distributiei binomiale introduce o eroare sistematica care poate fi compensata prin corectia de continuitate, extragand 0.5 din valoare absoluta a diferentei de la numaratorul scorului z.
. Daca evenimentele probabilistice pot avea mai mult decat doua posibilitati (de ex., adevarat-fals), probabilitatea cu care fiecare eveniment cade intr-una din categoriile posibile se supune distributiei multinomiale.
. Din cauza complexitatii procesului de evaluare a probabilitatilor multinomiale, este utilizata o estimare a acestora prin distributia chi-patrat. Numarul gradelor de libertate pentru distributia multinomiala este dat de numarul categoriilor minus 1.
. Testul chi-patrat are doua variante: (1) Testul chi-patrat al asocierii testeaza diferenta dintre valorile a doua variabile categoriale (nominale sau ordinale). (2) Testul chi patrat al corespondentei (goodness of fit) masoara diferenta ("potrivirea")dintre valorile unei variable categoriale si probabilitatile teoretice dinainte cunoscute ale acestor valori.
. Diferentele mari dintre frecventele observate si cele asteptate produc valori ridicate ale testului chi-patrat, care cad in zona dreapta (pozitiva) a distributiei de nul si
conduc la respingere a ipotezei de nul. Diferentele mici, produc valori ale testulu chi-patrat apropiate de zero, conducand la acceptarea ipotezei de nul. . Atunci cand fiecare dintre cele doua variabile au doar doua categorii, situatie in care frecventele asteptate sunt prea mici pentru a justifica o estimare chi-patrat, se utilizeaza testul exact Fischer.
EXERCITII
1. Pentru a verifica ipoteza ca exista o legatura intre numarul de internari psihiatrice si anotimp, au fost numarate internarile pentru fiecare anotimp, obtinandu-se urmatoarele valori: primavara=30; vara=40; toamna=20; iarna=10. Testati ipoteza ca internarile psihiatrice sunt inegal distribuite in functie de anotimp (pentru alfa=0.05).
2. Intr-un serviciu de psihologie clinica rezultatele mai multor psihologi in terapia unor pacienti cu tulburari severe au fost evaluate astfel: Ameliorare, Fara modificari, Inrautatire. rezultatele studiului se afla in tabelul alaturat:
|
|
psih. A |
psih. B |
psih. C |
psih. D |
psih. E |
|
Imbunatatire |
15 |
11 |
16 |
13 |
10 |
|
Nemodificat |
5 |
3 |
0 |
4 |
6 |
|
Inrautatire |
0 |
6 |
4 |
3 |
4 |
. Enuntati ipoteza cercetarii si ipoteza de nul
. Gasiti χ2 critic pentru α=0.01
. Testati ipoteza si prezentati rezultatul in format standard
. Calculati si interpretati coeficientul φc
Nota: Ignorati faptul ca doua din celulele tabelului au valoarea zero!
11/13
Intrebari pregatitoare pentru evaluarea partiala nr. 3 (15-17 ian.)
1. Care este coeficientul de determinare, daca r=-0.80?
2. In cazul testului t pentru esantioane dependente, pe ce scara se exprima valorile variabilei independente?
3. Care este numele celui care a introdus testul de corelatie pentru date parametrice?
4. Care este valoarea lui r pentru o corelatie perfecta?
5. Care dintre urmatorii coeficienti de corelatie este semnificativ: r=-0.70 (p=0.05) sau r=+0.70 (p=0.05)?
6. In ce caz o valoare a lui r apropiata de 0 (zero), indica, totusi, existenta unei corelatii intre variabile?
7. Distributia binomiala este
8. Care este probabilitatea lui P pentru un eveniment dihotomic aleator (DA/NU)?
9. Care este echivalentul parametric al testului z pentru proportii?
10. In cazul testului chi-patrat, frecventa asteptata se refera la
11. Testul chi-patrat goodness-of-fit se utilizeaza pentru a
12. Care sunt caracteristicile distributiei chi-patrat?
12/13
|
|
Tabelul χ2 (partiala, pana la 30 de grade de libertate)4
|
dfaria |
.100 |
.050 |
.025 |
.010 |
.005 |
|
1 |
2.70554 |
3.84146 |
5.02389 |
6.63490 |
7.87944 |
|
2 |
4.60517 |
5.99146 |
7.37776 |
9.21034 |
10.59663 |
|
3 |
6.25139 |
7.81473 |
9.34840 |
11.34487 |
12.83816 |
|
4 |
7.77944 |
9.48773 |
11.14329 |
13.27670 |
14.86026 |
|
5 |
9.23636 |
11.07050 |
12.83250 |
15.08627 |
16.74960 |
|
6 |
10.64464 |
12.59159 |
14.44938 |
16.81189 |
18.54758 |
|
7 |
12.01704 |
14.06714 |
16.01276 |
18.47531 |
20.27774 |
|
8 |
13.36157 |
15.50731 |
17.53455 |
20.09024 |
21.95495 |
|
9 |
14.68366 |
16.91898 |
19.02277 |
21.66599 |
23.58935 |
|
10 |
15.98718 |
18.30704 |
20.48318 |
23.20925 |
25.18818 |
|
11 |
17.27501 |
19.67514 |
21.92005 |
24.72497 |
26.75685 |
|
12 |
18.54935 |
21.02607 |
23.33666 |
26.21697 |
28.29952 |
|
13 |
19.81193 |
22.36203 |
24.73560 |
27.68825 |
29.81947 |
|
14 |
21.06414 |
23.68479 |
26.11895 |
29.14124 |
31.31935 |
|
15 |
22.30713 |
24.99579 |
27.48839 |
30.57791 |
32.80132 |
|
16 |
23.54183 |
26.29623 |
28.84535 |
31.99993 |
34.26719 |
|
17 |
24.76904 |
27.58711 |
30.19101 |
33.40866 |
35.71847 |
|
18 |
25.98942 |
28.86930 |
31.52638 |
34.80531 |
37.15645 |
|
19 |
27.20357 |
30.14353 |
32.85233 |
36.19087 |
38.58226 |
|
20 |
28.41198 |
31.41043 |
34.16961 |
37.56623 |
39.99685 |
|
21 |
29.61509 |
32.67057 |
35.47888 |
38.93217 |
41.40106 |
|
22 |
30.81328 |
33.92444 |
36.78071 |
40.28936 |
42.79565 |
|
23 |
32.00690 |
35.17246 |
38.07563 |
41.63840 |
44.18128 |
|
24 |
33.19624 |
36.41503 |
39.36408 |
42.97982 |
45.55851 |
|
25 |
34.38159 |
37.65248 |
40.64647 |
44.31410 |
46.92789 |
|
26 |
35.56317 |
38.88514 |
41.92317 |
45.64168 |
48.28988 |
|
27 |
36.74122 |
40.11327 |
43.19451 |
46.96294 |
49.64492 |
|
28 |
37.91592 |
41.33714 |
44.46079 |
48.27824 |
50.99338 |
|
29 |
39.08747 |
42.55697 |
45.72229 |
49.58788 |
52.33562 |
|
30 |
40.25602 |
43.77297 |
46.97924 |
50.89218 |
53.67196 |
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 6503
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved