| CATEGORII DOCUMENTE |
| Animale | Arta cultura | Divertisment | Film | Jurnalism | Muzica |
| Pescuit | Pictura | Versuri |
MODELUL RAMSEY-CASS-KOOPMANS
IPOTEZE:
Firmele.
Exista un numar mare de firme identice, fiecare avand o functie de productie de forma Y = F(K,AL). Firmele angajeaza lucratori si inchiriaza capital de pe piate competitive ale factorilor si vinde rezultatul pe piete competitive. Se considera A ca fiind dat si avand rata de crestere g. Firmele sunt maximizatoare de profit. Firmele sunt detinute de catre gospodarii, carora le revine profitul.
Gospodariile.
La fel multe Marimea fiecarei gospodarii creste cu rata n. Fiecare membru al gospodariei ofera o unitate de munca la un moment de timp. Gospodariile inchiriaza capitalul pe care il detin firmelor. Se face abstractie de uzura capitalului. Detinerile initiale de capital K(0)/H (H = numarul de gospodarii).
Gospodariile vor imparti veniturile lor intre consum si economisire a.i. sa maximizeze utilitatea pe timpul de viata.
Functia de utilitate a gospodariei:
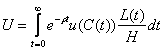 (1)
(1)
unde, C(t) este consumul fiecarui membru al gospodariei la timpul t, u = functie de utilitate instantanee, care confera utilitatea fiecarui membru la o data data. L(t) = populatia toatala din economie. L/H = nr. de persoane din gospodarie, iar u(C(t))L(t)/H utilitatea instantanee totala a gospodariei la momentul t.
Functia utilitatii instantanee ia forma:
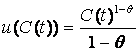 (2)
(2)
cu q > 0; r-n-(1-q)g > 0
Parametrul q determina de asemeni dorinta gospodariei de a-si schimba atitudinea fata de consum intre diferite perioade: cu cat mai mic este este q, cu atat mai incet va scadea utilitatea marginala pe masura ce consumul creste si astfel, cu atat mai mare va fi dorinta gospodariei de a permite consumului sau sa varieze in timp. Daca q este aproape zero => utilitatea este aproape liniara in C., si astfel gospodaria doreste sa accepte sa-si echilibreze consumul pentru a obtine avantaje din diferente mici dintre rata scontului si rata profitului adus de economisirile lor.
Comportamentul gospodariilor si al firmelor.
Firmele.
La fiecare moment de timp firmele folosesc stocuri de munca si capital, pe care la platesc cu produsul marginal, si vand rezultatul. Deoarece functia de productie are randamente de scara constante si economia este competitiva => firmele au profit zero. Productivitatea globala a capitalului este F(K, AL)/ K, respectiv, f (k). Nefind uzura a capitalului rata reala a profitului capitalului = castigulrile /unit de timp. Astfel rata reala a dobanzii la timpul t:
r(t) = f (k(t)) (3)
Productivitatea marginala a muncii efective este F(K, AL)/ AL, i.e. f(k) - k f (k).
Astfel salariul real/unitatea de munca efectiva:
w(t) = f(k(t)) - k(t) f (k(t)) (4)
Din moment ce productivitatea marginala a muncii (ca opus al muncii efective) este A F(K, AL)/ AL, venitul muncii unui muncitor la timpul t este A(t)w(t).
Problema optimizarii la nivel de gospodarie.
Gospodaria ia r si w ca fiind date.
Constrangerea bugetara a gospodariei: valoare prezenta a consumului din timpul de viata nu poate depasi averea initiala + valoarea prezenta a venitului muncii din timpul de viata.
Problema gospodariei este de a alege traiectoria lui c(t) pt a maximiza utilitatea duratei de viata in raport cu restrictia bugetara.
Dinamicile Economiei.
Cel mai convenabil este sa descrii evolutia economiei in termeni de k si c.
Dinamica lui c.
Deoarece r(t) = f (k(t)), avem:
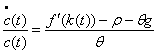 (5)
(5)
Consumul va depinde de k si c (fig. 2.1)
![]()
![]() c c
c c
![]()
![]()
(c > 0) (c < 0)
![]()
k* k
Fig. nr. 2.1. Dinamica lui c
Astfel c = 0 , cand f (k) = r qg. Fie k* - acest nivel a lui k.
Cand k > k* => f (k) < r qg => c < 0, si invers. (vezi figura 2.1). Sagetile arata directia de miscare a lui c.
Astfel c creste pt k < k* si scade pt k > k*. c = 0 la linia k = k*, i.e. c = constant.
Dinamica lui k.
Ca la Solow k = investitia reala - investitia de prag critic:
k = f(k(t)) - c(t) - (n+g) k(t) (2.23)
f
(k(t)) - c(t) - investitia reala.
k = 0 atunci cand consumul este egal cu diferenta dintre output real si linia investitiei de prag critic. Aceasta valoare a lui c este crescatoare in k pana la f (k) = n+g (regula de aur a nivelului lui k), apoi descreste.
Cand c depaseste nivelul pt care k = 0, k scade, invers pt c < decat acest nivel, k creste. Pt k suficient de larg, investitia de prag critic depaseste output, a. i. k este negativa pentru toate valorile pozitive a lui c. (vezi fig. 2.3, unde sagetile arata miscarile lui k).
![]()
![]()
![]()

 c (k <0)
c (k <0)
![]() k
k
k
Fig. 2.2 Dinamica lui k.
Diagrama de faza.
Figura 2.3 combina figurile 2.1. si 2.2. Sagetile arata diractiile de miscare ale lui c si k.
La stanga zonei lui si deasupra zonei lui k = 0, de exemplu, c este pozitiv si k este negativ. Astfel c creste si k scade, si astfel sagetile arata in sus spre stanga. Pe curbele c = 0 si k = 0, numai unul din c si k se modifica. Pe linia c = 0 deasupra zonei lui k = 0, de exemplu, c este constant si k scade; astfel sagata arata spre stanga. In punctul E atat c cat si k sunt zero; => nu exista miscare din acest punct. figura 2.3 are nivelul k* (nivelul lui k pt care c = 0) < nivelul ragulei de aur a lui k (valoarea lui k asociata varfului zonei k = 0). (Amintim ca k* e definit de f (k) = r qg, si regula de aur a lui k e definita de f (kGR) = n+g). Atunci cand f (k) < 0, k* < kGR <=> r qg > n+g. <=> r - n - (1-q)g > 0, conditie pentru non divergenta a utilitatii ciclului de viata. Din acest motiv k* este la stanga varfului curbei k
Fig. 2.3. Dinamica lui k si c.
![]()
![]()
![]()
![]() c c
c c
![]()
![]()
![]()

 E
E
![]()
![]()
![]()
![]() k
k
![]()
k* k
Figura 2.3 arata modul in care c si k trebuie sa evoluieze in timp pentru a satisface conditia de optimmizare intertemporala a gospodariei (ecuatia 2.22) si ecuatia cu privire la modificarea lui k in output si consum (ec. 2.23) fiind date valorile initiale ale lui c si k. Valoarea initiala a lui k este data dar a lui c trebuie determinata. Acest aspect este reprezentat in figura 2.4.
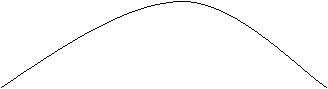
Fig. 2.4 Evolutia lui c si k pentru diferite valori initiale ale lui c.
![]()
![]()
![]()
![]()
![]()
![]()


![]()

![]()
![]()
![]()
![]() c
c
![]() A c' = 0
A c' = 0
F'
![]() E
E
B
![]() C k' = 0
C k' = 0
F
D
k(0) k* k
In mod concret se considera k(0) < k*. Figura arata ca traiectoria lui c si k in functie de diferite ipoteze cu privire la valoarea initiala a lui c.
Daca c(0) este deasupra curbei lui k = 0 (punctul A), c > 0 si k < 0; astfel economia se deplaseaza in sus si stanga diagramei.
Daca c(0) este luat astfel incat k = 0 (punctul B), economia incepe sa se miste direct in sus in spatiul (k,c), dupa care c > 0 si k < 0, iar economia se va misca spre stanga sus.
Daca economia incepe sa alunece sub zona k = 0 (punctul C), unde k > 0 dar mic (din moment ce k este o functie continua de c), iar c > 0. Astfel in acest caz economia se va misca initial in sus alunecand spre dreapta. Dupa ce intersecteaza zona k = 0, k devine negativ si economia este pe o traiectorie de crestere in care c sporeste si k descreste.
Punctul D arata cazul unui nivel al consumului initial foarte scazut. Aici, initial c > 0 si k > 0. Deoarece c este proportional cu c, cand c e mic c este la fel. Astfel c ramane scazut, si astfel economia traverseaza eventual linia
c = 0. La acest punct, c devine negativ si k ramane pozitiv. Astfel economia se va misca spre dreapta jos. Intrucat c si k sunt functii continue de c si k. rezulta ar trebui sa existe cateva puncte critice intre C si D, respectiv punctul F, astfel incat la acel nivel initial al lui c, economia converge spre un punct stabil, punctul E. Pentru orice nivel al consumului deasupra nivelului critic, curba lui k este atinsa inaite de linia c = 0, si astfel economia ajunge pe o traiectorie de crestere perpetua a consumului si o diminuare a capitalului.
Daca consumul este mai mic decat nivelul critic, zona c = 0 este atinsa mai intai, si astfel economia se plaseaza pe o cale de scadere a consumului si de crestere a capitalului. Dar daca consumul se afla chiar in nivelul critic, economia converge spre un punct unde atat c si k sunt constante. Toate aceste traiectorii satisfac ecuatiile ecuatiile de echilibru.
Pentru orice nivel initial pozitiv a lui k, exista un nivel initial unic al lui c care este consistent cu optimizarea intertemporala a gospodariei, dinamica stocului de capital, restrictia bugetara a gospodariei si cerinta de nenegativitate a lui k. Functia care da aceasta valoare initiala a lui c ca functie de k este numita calea sa (vezi figura 2.4). Pentru orice valoare de start a lui k, c initial ar trebui sa fie o valoare de pe aceasta cale. Economia se misca atunci de-a lungul caii sa spre punctul E.
Autorii modelului considera ca o traiectorie de crestere de tipul caii sa poate fi atinsa daca pietele functioneaza eficient si exista mobilitate a factorilor de productie, astfel incat acestia sa fie remunerati la nivelul valorii produsului marginal.
Calea sa.
Pentru orice nivel initial pozitiv a lui k, exista un nivel initial unic al lui c care este consistent cu optimizarea intertemporala a gospodariei, dinamica stocului de capital, restrictia bugetara a gospodariei si cerinta de nenegativitate a lui k. Functia care da aceasta valoare initiala a lui c ca functie de k = calea sa (vezi figura 2.5). Pentru orice valoare de start a lui k, c initial ar trebui sa fie o valoare de pe aceasta cale. Economia se misca atunci de-a lungul caii sa spre pct. E.
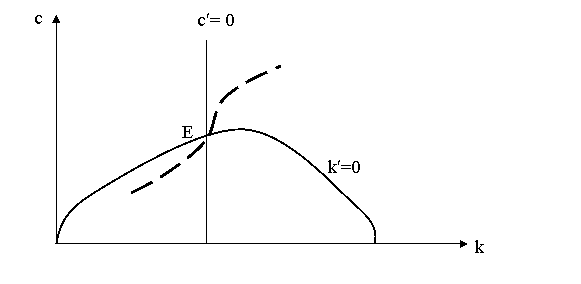
Fig. 2.5. Calea sa de crestere economica
Calea de crestere echilbrata. Proprietati.
Comportamentul
economiei odata ce converge spre pct. E e ideintic cu acela al economiei
lui Solow de pe o cale de crestere echilibrata. Capitalul, output
si consumul pe unitatea de munca efectiva sunt constante. Din
moment ce y si c sunt constante, rata economisirii, (y-c)/y este
Astfel implicatiile centrale ale modelului lui Solow cu privire la fortele conducatoare ale cresterii economice nu concorda cu ipoteyele sale asupra unei rate a econmisirii constante. Chiar si atunci cand economisirea este endogena, cresterea eficientei muncii ramane singura sursa posibila a cresterii persistente a output/lucrator. Si intrucat functia de productie este aceisi ca in modelul Solow; => diferente semnificative in output/lucrator pot sa apara din diferente in capitalul/lucrator, numai daca diferentele in capitalul/lucrator si in ratele profiturilor la capital sunt enorme.
Calea de crestere echilibrata si regula de aur a nivelului capitalului.
Singura diferenta notabila dintre calea de crestere echilibrata a lui Solow si Modelelel Ramssey-Cass-Koopmans este ca o cale de crestere echilibrata cu un stoc de capital peste nivelul regulii de aur nu-i posibil in cel din urma. In modelul Solow o rata a economisirii suficient de inalta face ca economia sa atinga o cale de crestere echilibrata cu proprietatea ca exista alternative fezabile care implica un consum mai inalt la fiecare moment.
In modelul R-C-K, dimpotriva, economisirea este derivata din comportamentul gospodariilor ale caroro utilitati depind de consumul lor si nu exista alternative. Ca un rezultat, nu poate sa fie un echilibru pt. economie de a urmari o cale unde consumul mai mare poate fi atins in fiecare perioada.; daca economia era pe o astfel de cale, gospodariile ar fi redus economisirea si ar fi obtinut avantaje dintr-o astfel de oportunitate. Aceasta poate fi vazut in diagrama de faza. (vezi iar fig.2.5). Daca stocul de capital depaseste nivelul regulii de aur (i.e. k(0) > k asociat cu varful zonei c, c = 0), consumul initial este peste cel necesar mentinerii lui k constant; astfel k < 0 => k se apropie gradual de k*, care este sub nivelul regulei de aur.
Faptul ca k* < stocul de capital al regulei de aur implica; economia nu converge spre o cale de crestere echilibrata care sa rezulte maximum nivel sustenabil al lui c.
Intuitia pt acest caz este cea mai clara pt. cazul g=0, a.i. nu exista crestere pe termen lung in consum si in output/lucrator. In acest caz k* este definit de f (k*) =r (vezi 2.22) si kGR e definit de f (kGR) = n, si ipoteza noastra ca r - n - (1-q)g > 0 se simplifica la r > n. Din moment ce k* < kGR, o crestere in economisire pornind de la k = k* ar face ca consumul/lucrator sa creasca peste nivelul anterior si sa ramana acolo (vezi fig. 1.5). Dar deoarece valoarea consumului prezent al gospodariei > decat a consumului viitor, beneficiul unei eventuale crestere permanenta in consum este limitat. La un asemenea punct - in special cand k > k* - compromisul dintre sacrificiul temporar pe termen scurt si castigul permanent pe termen lung este suficient nefavorabil ca acceptandu-l acesta reduce mai degraba decat creste utilitatea duratei de viata. Astfel k converge spre o valoare sub nivelul regulei de aur. Deoarece k* este nivelul optim a lui k pt economie pt a converge la o traiectorie de crestere echilibrata, acesta este cunoscut ca stocul de capital al regulei de aur modificate.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2791
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved