| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Ecuatia de transfer termic. Cazul unidimensional, stationar.
Se considera o bara, de lungime L si sectiune
tranversala A, incalzita la un capat (Fig. 1a). Caldura se transmite de-a
lungul barei astfel incat, la un moment dat, se va inregistra o crestere de
temperatura la capatul opus. Considerand ca bara are peretii izolati, caldura
se transmite in lungul abscisei x, printr-un process de conductie unidimensionala. Asa cum se obisnuieste in
literatura de specialitate, pentru demonstrarea ecuatiei tranferului termic, se
considera un volum elementar inchis (nu face schimb de masa cu exteriorul)
(Fig. 1b) situat intre abscisele x si ![]()
Pentru acest volum elementar se scrie Legea I a Termodinamicii:
![]() , (1)
, (1)
unde qi sunt fluxurile de caldura schimbate de volum cu exteriorul. Se respecta regula cunoscuta din Termodinamica potrivit careia un flux termic este pozitiv daca el este primit de sistem si este negativ in caz contrar; wi sunt lucrurile mecanice (pe unitatea de timp) schimbate de sistem cu exteriorul. Acestea sunt considerate negative daca sunt efectuate de exterior asupra sistemului si pozitive in caz contrar; E este energia interna a sistemului; t este timpul.
Deci, ecuatia (1) exprima faptul ca modificarea energiei interne a unui sistem inchis se datoreaza schimburilor de caldura si lucru mecanic cu exteriorul.
Pentru Fig. 1b, ecuatia (1) ia urmatoarea forma:
![]() . (2)
. (2)

Folosim
dezvoltarea in serie ![]() :
:
 ,
,
si o rescriem
pentru ![]() obtinand:
obtinand:
![]() . (3)
. (3)
Inlocuind (3) in (2), obtinem:
![]()
sau
![]() . (2')
. (2')
Legea lui Fourier stabileste ca fluxul termic este proportional si de sens opus cu gradientul de temperatura. Matematic, aceasta afirmatie este descrisa, in cazul unidimensional, de ecuatia (4)
![]() , (4)
, (4)
unde k este
conductivitatea termica a materialului [W/mK], proprietate ce se gaseste
experimental; temperatura ![]() este o functie de
spatiu si timp.
este o functie de
spatiu si timp.
Pentru demonstratie, se va considera
ca lucrul mecanic efectuat asupra sistemului (deci negativ ca valoare) este de
natura electrica. El se regaseste in sistem, datorita efectului Joule, sub
forma de aport (flux) termic, ![]() [W/m3]
[W/m3]
![]() . (5)
. (5)
Energia interna a sistemului este
![]() , (6)
, (6)
unde ρ este densitatea materialului, u este energia interna a sistemului (du=cdT, c este caldura specifica a materialului barei), astfel incat
![]() . (7)
. (7)
Inlocuind ecuatiile (47) in ecuatia (2') obtinem ecuatia tranferului termic in cazul unidimensional:
 .
.
Dupa simplificarea
cu ![]() , ecuatia devine:
, ecuatia devine:
 . (8)
. (8)
Daca
aria A este
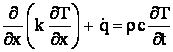 . (8')
. (8')
Considerand
conductivitatea termica a materialului ca fiind
 , (9)
, (9)
sau, impartind ecuatia de mai sus cu k,
 , (10)
, (10)
unde  [m2/s] este difuzivitatea termica a materialului.
[m2/s] este difuzivitatea termica a materialului.
Daca nu
exista surse interne de caldura, ![]() , ecuatia transferului termic devine
, ecuatia transferului termic devine
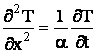 , (11)
, (11)
sau
![]() , (12)
, (12)
unde Δ este semnul folosit pentru operatorul lui
Daca, in
plus, campul termic este stationar![]() , ecuatia campului termic devine
, ecuatia campului termic devine
![]() . (13)
. (13)
Ecuatia (13) poarta denumirea de ecuatia lui
In urma unei demonstratii asemanatoare, in cazul unui transfer termic tridimensional, raportat la un sistem de referinta cartezian, xyz, ecuatia transferului termic se scrie
 . (14)
. (14)
Daca materialul este izotrop, conductivitatea termica
este o
![]() , (15)
, (15)
unde
 . (16)
. (16)
Daca nu exista surse interne de
caldura, iar campul termic este stationar, se regaseste ecuatia lui
Sisteme de coordonate cilindrice si sferice
Alegerea sistemului de coordonate este impus de geometria corpului ce se ia in considerare. Sunt cazuri in care sistemul de referinta cilindric (Fig. 2) sau cel sferic (Fig. 3) este recomandat pentru rezolvarea usoara, cu success, a unei probleme.


Fig. 2. Sistem de coordonate cilindric. Fig. 3. Sistem de coordonate sferic.
Sistem de coordonate cilindric: ecuatia transferului de caldura ia forma
 . (17)
. (17)
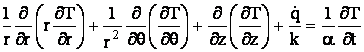 . (18)
. (18)
Sistem de coordonate sferic: ecuatia transferului de caldura se scrie

(19)
iar daca mediul este considerat omogen, ecuatia (19) devine
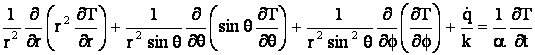 . (20)
. (20)
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1754
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved