| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Vibratii fortate
Un sistem alcatuit dintr-un corp legat elastic de un suport fix oscileaza liber daca este scos din starea de echilibru stabil prin aplicarea unui impuls sau prin deplasarea corpului si eliberarea lui.
Daca nu exista forte de frecare, oscilatia dureaza un timp nelimitat, iar pulsatia cu care corpul oscileaza este egala cu pulsatia proprie, calculata īn functie de masa corpului si rigiditatea legaturii lui elastice. In prezenta unui amortizor, amplitudinea miscarii oscilatorii se reduce treptat la zero.
Daca asupra aceluiasi sistem actioneaza permanent o forta de tip armonic, corpul va oscila ca urmare a prezentei fortei, dar pulsatia oscilatiei este impusa, īn cele din urma, de forta perturbatoare. Acest tip de actiune exterioara se numeste excitatie periodica. In tehnica es se īntālneste foarte frecvent, cel mai adesea datorita faptului ca piesele īn miscare de rotatie nu sunt echilibrate (centrul de rotatie nu coincide cu centrul de masa al corpului), sau oscilatiile sasiului se propaga la corpurile sprijite pe acesta. Alte dispozitive sunt construite tocmai cu scopul de a genera vibratii fortate, cum ar fi excitatoarele de vibratii.
Este posibil ca fortele periodice exterioare aplicate sistemului sa nu fie de tip armonic. Dar chiar si īn acest caz, deoarece sunt, totusi, periodice, ele pot fi scrise ca o suma de componente armonice, folosind algoritmii analizei Fourier.
In continuare se va studia miscarea corpurilor legate elastic, atunci cānd asupra lor actioneaza o forta exterioara de tip armonic.
1 Vibratii fortate ale unui sistem neamortizat
Modelul sistemului neamortizat, cu un grad de libertate, care este mentinut īn stare de vibratie ca urmare a actiunii fortei armonice exterioare Fo sin ωt, se poate vedea īn figura 2.29. Corpul de masa m este solicitat de forta armonica si de forta elastica din resort. Ecuatia de echilibru dinamic, ce reiese dupa izolarea corpului, este de forma :
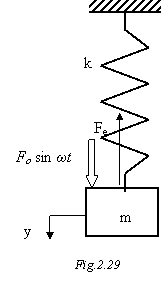
![]() ,
,
care se rescrie astfel:
![]()
Dupa impartirea termenilor ecuatiei la valoarea m, se obtine:
![]()
Pulsatia proprie a
sistemului este ![]() . Se noteaza
. Se noteaza ![]() pentru a reformula
ecuatia:
pentru a reformula
ecuatia:
![]()
Solutia generala a ecuatiei neomogene cu
coeficienti constanti este suma dintre solutia generala a
ecuatiei omogene, ![]() ,
,
si solutia particulara de forma ![]() Dupa
impunerea ca aceasta solutie sa verifice ecuatia
miscarii, se obtine :
Dupa
impunerea ca aceasta solutie sa verifice ecuatia
miscarii, se obtine :
![]() .
.
Cu acestea, pozitia instantanee a corpului care oscileaza este descrisa de relatia:
![]() .
.
Determinarea
constantelor A si B se poate face daca se impun pozitia ![]() si viteza
si viteza ![]() la momentul
initial:
la momentul
initial:

Constantele se evalueaza, ele fiind:
![]() si
si 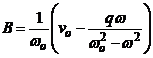
Ecuatia miscarii se scrie:

Forma analitica a legii
miscarii corpului de masa m
sub actiunea fortei armonice perturbatoare evidentiaza
existenta a doua pulsatii care guverneaza aceasta
miscare, ωo si ω. Prima este vibratia
proprie, determinata de caracteristicile intrinseci ale sistemului
masa-arc, iar a doua vibratie este impusa prin excitatia
exterioara. Prin urmare, corpul nu mai executa o oscilatie armonica.
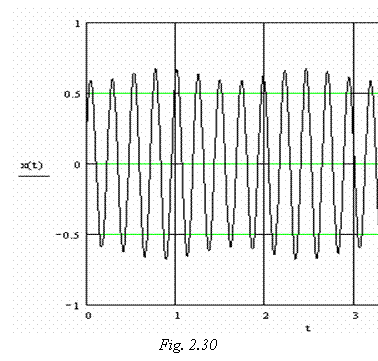
Evolutia īn timp a pozitiei
corpului care vibreaza, pentru un set de valori ale termenilor
ecuatiei (..), poate fi urmarita īn figura 2.30. Se poate
constata ca exista o curba īnfasuratoare a
graficului, de tip armonic. Miscarea īn ansamblu este periodica, dar
nu armonica.
Termenul din ecuatia de miscare, determinat de actiunea fortei perturbatoare, este:
![]() .
.
In functie de relatia de ordine dintre cele doua pulsatii, ωo si ω, se pot distinge trei modalitati de oscilatie, dupa cum urmeaza:
Cazul I. ω < ωo
Expresia termenului ![]() este (), deci
miscarea este īn faza cu
forta perturbatoare.
este (), deci
miscarea este īn faza cu
forta perturbatoare.
Cazul II. ω > ωo
Numitorul expresiei ![]() devine negativ, astfel
ca:
devine negativ, astfel
ca:
 ,
,
īn timp ce forta perturbatoare variaza armonic conform
relatiei![]() . Se constata ca
. Se constata ca ![]() si
si ![]() sunt defazate cu
unghiul π, care corespunde unei miscari
īn opozitie de faza a corpului relativ la excitatie.
sunt defazate cu
unghiul π, care corespunde unei miscari
īn opozitie de faza a corpului relativ la excitatie.
Cazul II. ω = ωo
In situatia īn care
excitatia exterioara are pulsatia egala cu pulsatia
proprie a sistemului oscilant masa resort, se manifesta fenomenul
de rezonanta. Termenul ![]() are numitorul egal cu
zero, ceea ce implica efectuarea unei operatii imposibile din punct
de vedere matematic. Aceasta semnifica, sub aspect fizic, inexistenta
unei miscari. In realitate, o coincidenta perfecta
īntre cele doua valori, ωo
si ω, nu este
posibila. Dar ele pot fi foarte apropiate, caz īn care,
are numitorul egal cu
zero, ceea ce implica efectuarea unei operatii imposibile din punct
de vedere matematic. Aceasta semnifica, sub aspect fizic, inexistenta
unei miscari. In realitate, o coincidenta perfecta
īntre cele doua valori, ωo
si ω, nu este
posibila. Dar ele pot fi foarte apropiate, caz īn care,

Se aplica regula
lui LHospital limitei din expresia anterioara, care se include īn cazul
de nedeterminare ![]() , si se obtine:
, si se obtine:
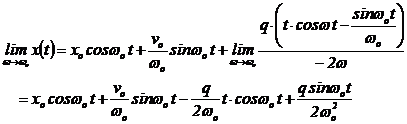
In expresia legii de
miscare a corpului, ![]() , exista trei termeni armonici multiplicati cu
coeficienti constanti care caracterizeaza o oscilatie cu
pulsatia unica ωo
si amplitudine finita. Un al patrulea termen armonic, egal cu
, exista trei termeni armonici multiplicati cu
coeficienti constanti care caracterizeaza o oscilatie cu
pulsatia unica ωo
si amplitudine finita. Un al patrulea termen armonic, egal cu ![]() , are coeficientul proportional cu timpul. Amplitudinea
oscilatiei determinate de acesta creste liniar īn timp, determinānd o crestere
extrem de accentuata a amplitudinii de oscilatie a corpului, īn
cursul oscilatiei. Teoretic, procesul de expansiune al amplitudinii
vibratiei dureaza la infinit. Limitarea fenomenului este data de
incapacitatea resortului real de a se deforma elastic īntr-un domeniu oricāt de
amplu. Conform curbei de īncarcare a arcului, la depasirea unei
anumite valori a deformatiei, materialul arcului nu va suporta tensiunile
mecanice care iau nastere īn interiorul lui si arcul se va rupe.
, are coeficientul proportional cu timpul. Amplitudinea
oscilatiei determinate de acesta creste liniar īn timp, determinānd o crestere
extrem de accentuata a amplitudinii de oscilatie a corpului, īn
cursul oscilatiei. Teoretic, procesul de expansiune al amplitudinii
vibratiei dureaza la infinit. Limitarea fenomenului este data de
incapacitatea resortului real de a se deforma elastic īntr-un domeniu oricāt de
amplu. Conform curbei de īncarcare a arcului, la depasirea unei
anumite valori a deformatiei, materialul arcului nu va suporta tensiunile
mecanice care iau nastere īn interiorul lui si arcul se va rupe.
 O
reprezentare grafica a evolutiei īn timp a unei astfel de
oscilatii a fost realizata īn figura 2.31, pentru un set oarecare de
valori ale constantelor ce intervin īn ecuatia miscarii, īn
regim de rezonanta. Se poate constata ca, dupa o
scurta evolutie descendenta a curbei
īnfasuratoare a graficului, nereprezentata, dar usor
de imaginat, amplitudinea creste rapid, īn timp.
O
reprezentare grafica a evolutiei īn timp a unei astfel de
oscilatii a fost realizata īn figura 2.31, pentru un set oarecare de
valori ale constantelor ce intervin īn ecuatia miscarii, īn
regim de rezonanta. Se poate constata ca, dupa o
scurta evolutie descendenta a curbei
īnfasuratoare a graficului, nereprezentata, dar usor
de imaginat, amplitudinea creste rapid, īn timp.
Sistemele reale nu cunosc o astfel de evolutie, unul dintre motive fiind prezentat anterior, legat de rezistenta mecanica limitata a materialului arcului supus la deformatii din ce īn ce mai mari. Un al doilea fapt care intervine īntr-un sistem real este forta de frecare din materialul arcului, care este, īnsa de natura histeretica. Daca sistemul masa-arc este prevazut suplimentar cu un amortizor vāscos, comportarea vibratorie a sistemului elastic se modifica, dupa cum se va vedea īn paragraful urmator.
1 Vibratii fortate ale unui sistem amortizat
 Modelul sistemului amortizat,
avānd un grad de libertate, acela de miscare de translatie, sau cu
miscare de rotatie, este constituit dintr-un corp de masa m legat elastic de un suport fix. Corpul este mentinut īn stare de
vibratie ca urmare a actiunii fortei armonice exterioare de
pulsatie ω, notata Fo sin ωt, dupa cum se poate vedea īn figura 2.32. Corpul de
masa m este solicitat de
forta armonica, de forta elastica din resort si de
forta de frecare vāscoasa din amortizor. Ecuatia de echilibru
dinamic, ce se poate scrie dupa izolarea corpului, este de forma :
Modelul sistemului amortizat,
avānd un grad de libertate, acela de miscare de translatie, sau cu
miscare de rotatie, este constituit dintr-un corp de masa m legat elastic de un suport fix. Corpul este mentinut īn stare de
vibratie ca urmare a actiunii fortei armonice exterioare de
pulsatie ω, notata Fo sin ωt, dupa cum se poate vedea īn figura 2.32. Corpul de
masa m este solicitat de
forta armonica, de forta elastica din resort si de
forta de frecare vāscoasa din amortizor. Ecuatia de echilibru
dinamic, ce se poate scrie dupa izolarea corpului, este de forma :
![]() ,
,
care se rescrie astfel:
![]()
Dupa impartirea termenilor ecuatiei la valoarea m, se obtine:
![]()
Pulsatia proprie a
sistemului este ![]() . Se fac urmatoarele notatii,
. Se fac urmatoarele notatii, ![]() si
si ![]() , pentru a reformula ecuatia:
, pentru a reformula ecuatia:
![]()
Solutia generala a ecuatiei neomogene cu
coeficienti constanti este suma dintre solutia generala a
ecuatiei omogene, ![]() ,a carei expresie este
,a carei expresie este ![]() ,
,
si solutia particulara de forma xp, adica,
![]()
Datorita amortizarii, vibratia indusa prin prezenta termenului omogen este amortizata rapid de sistem, dupa cum s-a vazut la paragraful 2.2.1. De aceea, termenul omogen se spune ca poate caracteriza numai asa-numitul regin tranzitoriu. Singurul termen al solutiei ecuatiei de echilibru care descrie miscarea corpului la momente de timp din afara domeniului tranzitoriu este solutia particulara. Ea se presupune a fi de forma :
![]()
deoarece ea reprezinta o miscare armonica simpla cu pulsatia ω egala cu cea a fortei excitatoare, iar miscarea survine la un moment ulterior aplicarii acestei forte exterioare, fapt exprimat prin defazajul negativ (-φ Se impune ca aceasta solutie sa verifice ecuatia miscarii. Expresiile vitezei instantanee,
![]() ,
,
si a acceleratiei instantanee,
![]() ,
,
se introduc īn ecuatia de miscare. Se obtine:
![]()
Termenii
egalitatii sunt vectori orientati īn felul urmator, relativ
la vectorul care descrie comportarea elastica, ![]() :
:

Reprezentarea acestor vectori
īntr-un sistem de axe ortogonale se poate analiza īn figura 2.33.
In conformitate cu reprezentarea vectoriala din figura 2.33, se poate scrie:
![]()
ceea ce este echivalent cu:

Defazajul φ rezulta din aceeasi reprezentare vectoriala:
![]()
Cu aceste consideratii, se poate scrie ecuatia miscarii corpului de masa m īn regim stationar:
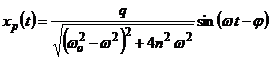 ,
,
unde ![]() .
.
Daca se face
notatia deja cunoscuta, ![]() , expresia legii miscarii īn regim stationar va fi:
, expresia legii miscarii īn regim stationar va fi:
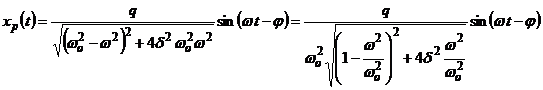
Daca se tine cont si de termenul care descrie oscilatia īn regimul tranzitoriu, legea de miscare a corpului care oscileaza fortat, īn cazul prezentei unei amortizari este:

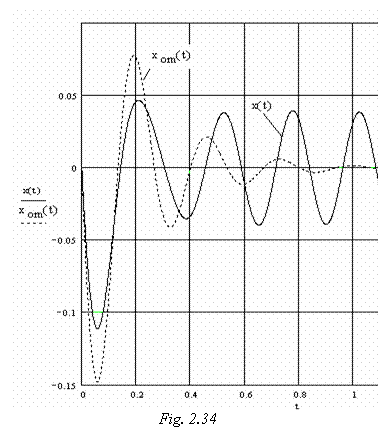
O reprezentare grafica a evolutiei īn timp a unei astfel de oscilatii a fost realizata īn figura 2.34. Curba cu linie continua corespunde miscarii combinate a corpului sub actiunea fortei exterioare, a carei pulsatie difera de pulsatia proprie a sistemului corp-element elastic. Curba trasata cu linie īntrerupta prezinta evolutia acelei componente a raspunsului sistemului amortizat, termenul solutie a ecuatiei onogene, care se manifesta doar pe durata regimului tranzitoriu. In cazul considerat, durata acestui regim este de circa 1,2 s.
Dupa ce s-a
scurs intervalul de timp al regimului
tranzitoriu, se poate spune ca oscilatia este descrisa numai de
expresia:
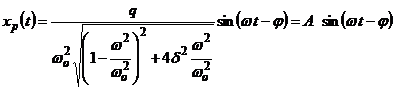 ,
,
unde prin A s-a notat amplitudinea constanta a oscilatiei caracteristica regimului stationar,
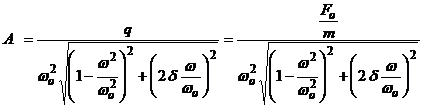
Valoarea amplitudinii A se modifica atunci cānd pulsatia fortei excitatoare ωo variaza crescator de la zero. Pentru a putea studia o valoare adimensionala care are o evolutie similara, se introduce deformatia statica As a resortului de rigiditate k, sub actiunea unei forte egale cu valoarea amplitudinii fortei excitatoare, Fo.
![]()
Prin urmare, se introduce raportul adimensional al marimilor A si As:
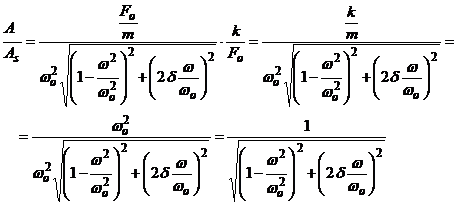
Graficul finctiei
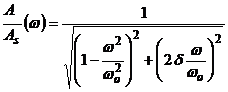 ,
, ![]()
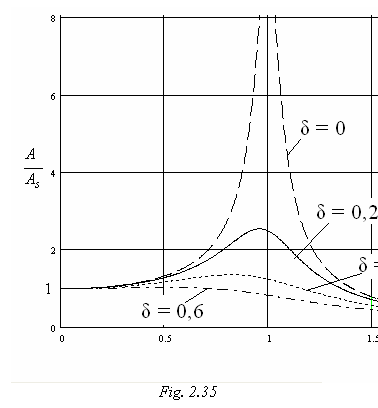
a fost trasat īn figura 2.35. Acest grafic va fi explicat īn cele ce urmeaza.
In sistemele mecanice reale, pulsatia
sistemului excitator nu creste brusc de la valoarea zero la valoarea de
regim ω deoarece aceasta crestere instantanee ar echivala
cu existenta unor acceleratii liniare sau unghiulare infinite. Daca
excitatia are, īn regim normal de lucru, pulsatia egala cu
pulsatia proprie a sistemului oscilant, ωo atingerea acestei
valori a pulsatiei excitatoare se face treptat. Pe masura ce ω
tinde spre ωo, amplitudinea
oscilatiei ia valori din ce īn ce mai mari, limitate doar ca urmare
a existentei la numitor al termenului nenul ![]() introdus de
coeficientul de frecare al dispozitivului amortizor cu frecare vāscoasa. In
absenta amortizorului, raportul adimensional al amplitudinilor tinde spre
infinit, dupa cum arata curba corespunzatoare lui δ = 0,
ceea ce echivaleaza cu distrugerea sistemului oscilant. In
aplicatiile practice curente, este de dorit sa se evide amplificarea
oscilatiei, pentru a creste fiabilitatea dispozitivului solicitat de
excitatia armonica fortata. De aceea, se evita
amplasarea regimului de lucru al pulsatiei excitatoare īn domeniul
īnvecinat, la stānga sau la dreapta, pulsatiei proprii ωo.
introdus de
coeficientul de frecare al dispozitivului amortizor cu frecare vāscoasa. In
absenta amortizorului, raportul adimensional al amplitudinilor tinde spre
infinit, dupa cum arata curba corespunzatoare lui δ = 0,
ceea ce echivaleaza cu distrugerea sistemului oscilant. In
aplicatiile practice curente, este de dorit sa se evide amplificarea
oscilatiei, pentru a creste fiabilitatea dispozitivului solicitat de
excitatia armonica fortata. De aceea, se evita
amplasarea regimului de lucru al pulsatiei excitatoare īn domeniul
īnvecinat, la stānga sau la dreapta, pulsatiei proprii ωo.
Proiectarea unui sistem mecatronic impune cunoasterea īnca din faza de concept a pulsatiilor proprii ale sistemului elastic pentru a evita amplasarea regimului de lucru īn vecinatatea acestora.
1 Vibratiile fortate induse de forta centrifuga unui sistem amortizat
Piesele īn miscare de rotatie neechilibrate dinamic genereaza o forta centrifuga de inertie, care actioneaza ca forta excitatoare īn sistemele mecanice. Forta centrifuga este de tip armonic si are valoarea maxima proportionala cu patratul vitezei unghiulare, care corespunde pulsatiei excitatoare:
![]() ,
,
unde mr este masa piesei rotitoare, iar e este valoarea excentricitatii axei de rotatie fata de axa de simetrie a corpului rotiror.
Amplitudinea oscilatiei induse de forta centrifuga se determina cu ajutorul relatiei (),
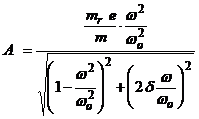
Privind expresia
(.) ca o functie de variabila ![]() , putem afla la ce valoare a raportului pulsatiilor,
valoarea amplitudinii atinge maximul, prin rezolvarea ecuatiei
, putem afla la ce valoare a raportului pulsatiilor,
valoarea amplitudinii atinge maximul, prin rezolvarea ecuatiei 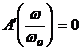 :
:
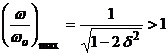
Interpretarea acestui
rezultat permite īntelegerea faptului ca amplitudinea de
oscilatie are un vārf situat la pulsatii mai mari ca pulsatie
proprie, ![]() , iar vārful de amplitudine se īndeparteaza de ωo spre
dreapta, pe masura ce amortizarea creste. Graficele trasate īn
figura 2.36 arata ca expresia raportului adimensionl al
amplitudinilor tinde catre valoarea 1, atunci cānd raportul
pulsatiilor tinde la valori mult mai mari ca 1. Acest fapt se poate
interpreta astfel: la cresterea turatiei de lucru a unui element rotitor
neechilibrat dinamicpeste frecventa de rezonanta, amplitudinea
oscilatiilor se reduce treptat, tinzānd spre valoarea dezechilibrarii
statice.
, iar vārful de amplitudine se īndeparteaza de ωo spre
dreapta, pe masura ce amortizarea creste. Graficele trasate īn
figura 2.36 arata ca expresia raportului adimensionl al
amplitudinilor tinde catre valoarea 1, atunci cānd raportul
pulsatiilor tinde la valori mult mai mari ca 1. Acest fapt se poate
interpreta astfel: la cresterea turatiei de lucru a unui element rotitor
neechilibrat dinamicpeste frecventa de rezonanta, amplitudinea
oscilatiilor se reduce treptat, tinzānd spre valoarea dezechilibrarii
statice.
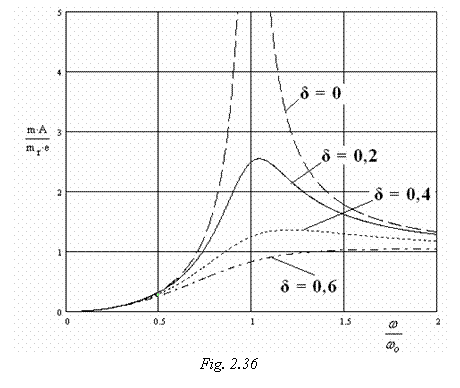
Cu cāt amortizarea vāscoasa
este mai mare, cu atāt aceasta comportare este atinsa la
pulsatii mai mici, care corespund unor turatii mai mici de lucru.
Acest lucru este foarte important īn practica, daca se doreste reducerea
vibtratiilor unui sistem. De exemplu, cresterea amortizarii nu
modifica semnificativ comportarea sistemului, daca frecventa de
excitatie nu este situata īn vecinatatea rezonantei.
Inainte de a incerca reducerea nivelului de vibratie īntr-un dispozitiv mecatronic sau orice alta structura, trebuie luate masuri pentru diminuarea vibratiei excitatoare la sursa acesteia. Este evident ca numte dispozitive sau procese genereaza forte perturbatoare de un tip sau altul, dar frecventa fortei perturbatoare nu trebuie sa fie egala cu frecventa proprie, nici sa se situeze īn vecinatatea precventei proprii. In caz contrar apare fenomenul de rezonanta, īn urma caruia se vor manifesta amplitudini mari de vibratie si tensiuni mecanice de tip dinamic, īnsotite de zgomot si fenomene asociate de oboseala a materialelor.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 309
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved