| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
ALGEBRA
Numere
reale ![]()
Formule de calcul prescurtat Fie ![]() , atunci avem:
, atunci avem:
![]()
![]()
![]()
![]()
![]()
![]()
Modulul unui numar real Fie ![]() , de numeste modulul lui
, de numeste modulul lui
![]() (si se noteaza
(si se noteaza ![]() ), numarul real
), numarul real
![]()
Proprietati
![]() ,
, ![]()
![]()
![]()
![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
Fie
![]() , se numeste partea
intreaga a lui
, se numeste partea
intreaga a lui ![]() (si se noteaza
(si se noteaza ![]() ), cel mai mare numar intreg mai mic sau egal cu
), cel mai mare numar intreg mai mic sau egal cu ![]() , se numeste partea
fractionara a lui
, se numeste partea
fractionara a lui ![]() (si se noteaza
(si se noteaza ![]() ) numarul
) numarul ![]() .
.
Proprietati:
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
Radicali, puteri cu exponent rational
Fie
![]() si
si ![]() un numar natural par. Se numeste radical de ordinul
un numar natural par. Se numeste radical de ordinul ![]() din
din ![]() (se noteza
(se noteza ![]() , un numar
, un numar ![]() cu proprietatea ca
cu proprietatea ca ![]() . Fie
. Fie ![]() si
si ![]() un numar natural impar. Se numeste radical de ordinul
un numar natural impar. Se numeste radical de ordinul ![]() din
din ![]() (se noteza
(se noteza ![]() , un numar
, un numar ![]() cu proprietatea ca
cu proprietatea ca ![]() .
.
Observatie. Daca in exercitii
(ecuatii sau inecuatii) intalnim expresii de forma ![]() (radical de ordin par) se impune conditia de existenta a
radicalului:
(radical de ordin par) se impune conditia de existenta a
radicalului: ![]() . Daca avem radicali de ordin impar, pentru acestia nu se
impun conditii de existenta.
. Daca avem radicali de ordin impar, pentru acestia nu se
impun conditii de existenta.
Proprietati Fie ![]() ,
, ![]() si
si ![]() . Atunci avem:
. Atunci avem:
![]() , daca
, daca ![]() este par
este par
![]() , daca
, daca ![]() este impar
este impar
![]()
![]()
![]()
![]()
Transformarea radicalilor compusi in radicali simpli :
![]() , unde
, unde ![]() .
.
Fie
![]() si
si ![]() , atunci
, atunci ![]() .
.
Proprietati Fie ![]() si
si ![]() , atunci:avem
, atunci:avem
![]()
![]()
![]()
![]()
![]()
![]()
Inegalitati remarcabile
Inegalitatea mediilor Fie ![]() si
si ![]() , notam:
, notam: ![]() ,
, ![]() ,
, 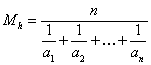 , avem:
, avem: ![]() cu egalitate pentru
cu egalitate pentru ![]() .
.
Observatie. In cazul ![]() pentru
pentru ![]() , avem:
, avem: ![]() .
.
Inegalitatea lui
Bernoulli Fie ![]() si
si ![]() , atunci
, atunci ![]() .
.
Multimi
Fie
![]() o mutime si
o mutime si ![]() doua submultimi ale lui
doua submultimi ale lui ![]() .
.
Complementara multii ![]() este multimea
este multimea ![]()
Intersectia multimilor ![]() si
si![]() este multimea
este multimea ![]()
Reuniunea multimilor ![]() si
si![]() este multimea
este multimea ![]()
Diferenta multimilor ![]() si
si![]() este multimea
este multimea ![]()
Produsul cartezian al multimilor ![]() si
si![]() este multimea
este multimea ![]()
Se
numeste cardinanlul unei multimi ![]() (si se noteaza
(si se noteaza ![]() sau
sau ![]() ), numarul elementelor multimii
), numarul elementelor multimii ![]() . Avem:
. Avem:
![]()
![]()
Metoda inductiei matematice
Fie
![]() o propozitie care
depinde de numarul
o propozitie care
depinde de numarul ![]() . Daca avem:
. Daca avem:
atunci
![]() este adevarata
este adevarata ![]() .
.
Progresii aritmetice si geometrice
Se numeste progresie
aritmetica un sir in care fiecare termen, mai putin primul, se obtine din
precedentul adunat cu un numar constant ![]() numit ratie.
numit ratie.
Notatie: ![]()
Proprietati
![]() ,
, ![]() ;
; ![]() constant,
constant, ![]() ;
;
Formula termenului
general
: ![]() ,
, ![]() ;
;
![]() (proprietatea care caracterizeaza progresiile aritmetice),
(proprietatea care caracterizeaza progresiile aritmetice), ![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() .
.
Se numeste progresie
geometrica un sir in care fiecare termen, mai putin primul, se obtine din
precedentul inmultit cu un numar constant nenul ![]() , numit ratie.
, numit ratie.
Notatie: ![]()
Proprietati
![]() ,
, ![]() ;
; ![]() constant,
constant, ![]() ;
;
Formula termenului
general
: ![]() ,
, ![]() ;
;
![]() (proprietatea care caracterizeaza progresiile geometrice) , iar
daca sirul are termeni pozitivi, avem:
(proprietatea care caracterizeaza progresiile geometrice) , iar
daca sirul are termeni pozitivi, avem:![]() ,
,![]() ,
,![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
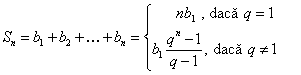 .
.
Functii
Fie
![]() si
si ![]() doua multimi nevide.
Spunem ca am definit o functie pe
multimea
doua multimi nevide.
Spunem ca am definit o functie pe
multimea ![]() cu valori in multimea
cu valori in multimea ![]() , daca printr-un procedeu oarecare facem ca fiecarui element
, daca printr-un procedeu oarecare facem ca fiecarui element ![]() sa-i corespunda un
singur element
sa-i corespunda un
singur element ![]() . (O functie definita pe
. (O functie definita pe ![]() cu valori in
cu valori in ![]() se noteaza
se noteaza ![]() ,
, ![]() se numeste domeniul de definitie, iar
se numeste domeniul de definitie, iar ![]() se numeste codomeniul).
se numeste codomeniul).
Functia
![]() , definita prin
, definita prin ![]() ,
, ![]() , se numeste aplicatia
identica a multimii
, se numeste aplicatia
identica a multimii ![]() .
.
Fie
![]() ,
, ![]() doua functii. Spunem
ca functiile
doua functii. Spunem
ca functiile ![]() sunt egale (si scriem
sunt egale (si scriem ![]() ) daca :
) daca :
1.
![]() (au acelasi domeniu de
definitie) ;
(au acelasi domeniu de
definitie) ;
2.
![]() (au acelasi codomeniu)
;
(au acelasi codomeniu)
;
3.
![]() (functiile coincid in
fiecare punct din domeniu).
(functiile coincid in
fiecare punct din domeniu).
Operatii cu functii Fie ![]() o multime nevida si
o multime nevida si ![]() doua functii, atunci:
doua functii, atunci:
![]() ,
, ![]() ,
, ![]() se numeste functia suma a lui
se numeste functia suma a lui ![]() si
si ![]() .
.
![]() ,
, ![]() ,
, ![]() se numeste functia produs a lui
se numeste functia produs a lui ![]() si
si ![]() .
.
Daca ![]() ,
, ![]() , atunci
, atunci ![]() ,
, ![]() ,
, ![]() se numeste functia cat a lui
se numeste functia cat a lui ![]() si
si ![]() .
.
Fie ![]() si
si ![]() doua functii. Functia
doua functii. Functia ![]() definita prin
definita prin ![]() ,
, ![]() , se numeste compusa
lui
, se numeste compusa
lui ![]() cu
cu ![]() .
.
Fie
![]() o functie
o functie
Se numeste numerica daca
![]() .
.
Se numeste imaginea
functiei ![]() multimea notata
multimea notata ![]() si egala cu
si egala cu ![]() .
.
Se numeste graficul
functiei ![]() multimea
multimea ![]() .
.
Se numeste injectiva,
daca ![]() cu
cu ![]() .
.
Se numeste surjectiva
daca pentru orice ![]() , exista un
, exista un ![]() astfel incat
astfel incat ![]() .
.
Se numeste bijectiva daca este atat injectiva cat si surjectiva.
Se numeste inversabila
daca exista o functie ![]() astfel incat
astfel incat ![]() si
si ![]() . (Functia
. (Functia ![]() din definitie se
numeste inversa functiei
din definitie se
numeste inversa functiei ![]() si se noteaza cu
si se noteaza cu ![]() ).
).
Teorema. O functie este inversabila daca si numai daca este bijectiva.
Observatie. Pentru a determina intersectia
graficului unei functii cu axa ![]() , rezolvam ecuatia
, rezolvam ecuatia ![]() , iar pentru a determina intersectia graficului functiei cu
axa
, iar pentru a determina intersectia graficului functiei cu
axa ![]() , calculam
, calculam ![]() , daca 0 se gaseste in domeniul de definitie al functiei.
, daca 0 se gaseste in domeniul de definitie al functiei.
O
multime ![]() se numeste simetrica in raport cu 0 (zero) daca
pentru orice
se numeste simetrica in raport cu 0 (zero) daca
pentru orice ![]() si
si ![]() .
.
Fie
![]() o multime simetrica in
raport cu zero. Functia
o multime simetrica in
raport cu zero. Functia ![]() se numeste:
se numeste:
para daca ![]() .
.
impara daca ![]() .
.
Observatie. Graficul unei functii
pare este simetric fata de axa ![]() , iar cel al unei functii impare este simetric in raport cu
originea O.
, iar cel al unei functii impare este simetric in raport cu
originea O.
Fie
![]() o functie de variabila
reala si
o functie de variabila
reala si ![]() . Spunem ca functia
. Spunem ca functia ![]() este:
este:
strict crescatoare pe ![]() daca :
daca :  ;
;
strict descrescatoare pe ![]() daca :
daca :  ;
;
crescatoare pe ![]() daca :
daca :  ;
;
descrescatoare pe ![]() daca :
daca :  .
.
Observatie. O functie ![]() strict crescatoare pe
strict crescatoare pe ![]() sau strict
descrescatoare pe
sau strict
descrescatoare pe ![]() se numeste functie strict monotona pe
se numeste functie strict monotona pe ![]() . O functie
. O functie ![]() crescatoare pe
crescatoare pe ![]() sau descrescatoare pe
sau descrescatoare pe ![]() se numeste monotona
pe
se numeste monotona
pe ![]() . Daca
. Daca ![]() este strict monotona
(sau monotona) pe
este strict monotona
(sau monotona) pe ![]() (pe tot domeniul de
definitie) spunem simplu ca
(pe tot domeniul de
definitie) spunem simplu ca ![]() este strict monotona
(sau monotona) fara a mai indica multimea.
este strict monotona
(sau monotona) fara a mai indica multimea.
O
functie monotona pe o multime ![]() , ramane monotona pe orice submultime a sa.
, ramane monotona pe orice submultime a sa.
Fie
functia ![]() , unde
, unde ![]() interval. Se spune ca
functia
interval. Se spune ca
functia ![]() este
este
convexa pe ![]() , daca
, daca ![]() si
si ![]() , cu
, cu ![]() , avem:
, avem:
![]() .
.
concava pe ![]() ,daca
,daca ![]() si
si ![]() , cu
, cu ![]() , avem :
, avem :
![]() .
.
Observatie. 1. Daca ![]() este convexa pe
este convexa pe ![]() , atunci pentru
, atunci pentru ![]() se obtine:
se obtine:
![]() ,
, ![]() , iar daca f este concava pe
, iar daca f este concava pe ![]() , atunci
, atunci ![]() ,
, ![]() .
.
2. Interpretarea geometrica a concavitatii si convexitatii :
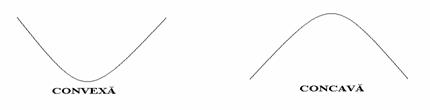
In limbaj trivial spunem despre graficul functiei convexe ca " tine apa " in timp ce graficul functiei concave " nu tine apa ".
Functia de
gradul I
![]() ,
, ![]() , unde
, unde ![]() ,
, ![]() .
.
Rezolvarea ecuatiei ![]() , unde
, unde ![]() .
.
- daca ![]() , atunci
, atunci ![]() (ecuatia nu admite
radacini)
(ecuatia nu admite
radacini)
Semnul functiei de gradul
I ![]() ,
, ![]() , unde
, unde ![]() ,
, ![]() :
:
|
|
|
|
|
semn contrar
lui |
Monotonia functiei de
gradul I:
Daca ![]() , atunci
, atunci ![]() este strict
crescatoare, iar daca
este strict
crescatoare, iar daca ![]() , atunci
, atunci ![]() este strict
descrescatoare.
este strict
descrescatoare.
Graficul: Este o dreapta, pentru reprezentarea grafica sunt necesare 2 puncte distincte.
Functia de
gradul II ![]() ,
, ![]() , unde
, unde ![]() ,
, ![]() .
.
Forma canonica: ![]()
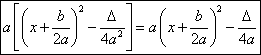 , unde
, unde ![]() .
.
Rezolvarea ecuatiei ![]() , unde
, unde ![]() ,
, ![]() . Calculam
. Calculam ![]() , distingem cazurile:
, distingem cazurile:
|
|
Ecuatia nu are radacini reale, in schimb are doua radacini complexe conjugate:
|
|
|
Ecuatia are doua
radacini reale egale: |
|
|
Ecuatia are doua
radacini reale distincte: |
Relatiile lui
Viète: ![]() ,
, ![]() . Mai avem:
. Mai avem: ![]() ,
, ![]() ,
, ![]() , daca radacinile sunt
nenule:
, daca radacinile sunt
nenule: ![]() .
.
Observatie. Orice ecuatie de gradul
2 se poate scrie sub forma ![]() , unde
, unde ![]() si
si ![]() reprezinta suma si
respectiv produsul radacinilor ecuatiei.
reprezinta suma si
respectiv produsul radacinilor ecuatiei.
Descompunerea trinomului ![]() , unde
, unde ![]() ,
, ![]() .
.
|
|
|
Nu se descompune. |
|
|
|
|
|
|
|
|
|
|
|
|
Semnul functiei de gradul
II. In
functie de valorile lui ![]() distingem cazurile:
distingem cazurile:
|
|
|
|
|
|
semnul lui a |
|
|
|
|
|
|
|
semnul lui a |
|
|
|
|
|
|
|
semnul lui a
|
Extremul functiei de gradul II. Monotonia functiei de gradul II.
Graficul: este o parabola.
Functia exponentiala (de baza ![]() )
) ![]() ,
, ![]() , unde
, unde ![]() ,
, ![]() .
.
Rezolvarea ecuatiei ![]() , unde
, unde ![]() ,
, ![]() ,
, ![]() .
.
Semnul functiei
exponentiale: ![]() (este strict
pozitiva),
(este strict
pozitiva), ![]() ,
, ![]() ,
, ![]() .
.
Monotonia: Este strict crescatoare
(pe ![]() ) daca
) daca ![]() si strict
descrescatoare (pe
si strict
descrescatoare (pe ![]() ) daca
) daca ![]() .
.
Graficul functiei exponentiale
trece prin punctul ![]() , adica
, adica ![]() ,
, ![]() ,
, ![]() .
.
Observatie. Functia exponentiala de
baza ![]() este bijectiva, deci
inversabila, inversa acesteia este functia
logaritmica de baza
este bijectiva, deci
inversabila, inversa acesteia este functia
logaritmica de baza ![]() .
.
Functia logaritmica (de baza ![]() )
) ![]() ,
, ![]() , unde
, unde ![]() ,
, ![]() .
.
Observatie. Daca ![]() , atunci
, atunci ![]() se noteaza
se noteaza ![]() , daca
, daca ![]() , atunci
, atunci ![]() se noteaza
se noteaza ![]() .
.
Rezolvarea ecuatiei ![]() ,unde
,unde ![]() ,
, ![]() ,
, ![]() . Ecuatia are solutie
unica
. Ecuatia are solutie
unica ![]() ,
, ![]() .
.
Semnul functiei logaritmice:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Monotonia: Este strict crescatoare
(pe ![]() ) daca
) daca ![]() si strict
descrescatoare (pe
si strict
descrescatoare (pe ![]() ) daca
) daca ![]() .
.
Proprietati : Daca ![]() , atunci :
, atunci :
![]() ,
, ![]() ;
; ![]() ,
, ![]() ;
; ![]() ;
; ![]() ;
;
![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
, ![]() ;
;
![]() ;
; ![]() ,
, ![]() ,
, ![]() .
.
Graficul functiei exponentiale
trece prin punctul ![]() , adica
, adica ![]() ,
, ![]() ,
, ![]() .
.
Observatie. In ecuatii sau
exercitiile in care apar expresii de forma : ![]() se impun conditiile de
existenta :
se impun conditiile de
existenta : 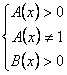 .
.
Elemente de combinatorica
Se numeste multime ordonata, o multime impreuna cu o ordine bine determinata de dispunere a elementelor sale.
Permutari de ![]() elemente, notate cu
elemente, notate cu ![]() , reprezinta numarul multimilor ordonate formate cu
elementele unei multimi cu
, reprezinta numarul multimilor ordonate formate cu
elementele unei multimi cu ![]() elemente. Numarul
permutarilor de
elemente. Numarul
permutarilor de ![]() elemente este de
elemente este de
![]() .
.
Aranjamente de ![]() elemente luate cate
elemente luate cate ![]() , notate
, notate ![]() , reprezinta numarul submultimilor ordonate formate cu
, reprezinta numarul submultimilor ordonate formate cu ![]() elemente din
elementele unei multimi cu
elemente din
elementele unei multimi cu ![]() elemente. Numarul
aranjamentelor de
elemente. Numarul
aranjamentelor de ![]() luate cate
luate cate ![]() este
este ![]() .
.
Combinari de ![]() elemente luate cate
elemente luate cate ![]() , notate
, notate ![]() , reprezinta numarul submultimilor cu k elemente ale unei
multimi cu
, reprezinta numarul submultimilor cu k elemente ale unei
multimi cu ![]() elemente. Numarul
combinarilor de
elemente. Numarul
combinarilor de ![]() luate cate
luate cate ![]() este
este ![]() .
.
Proprietati :
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Binomul lui Newton
![]() .
.
Formula termenului general :
![]() ;
;
Formula de recurenta : ![]() .
.
Fie ![]() o multime finita cu
o multime finita cu ![]() elemente. Atunci:
elemente. Atunci:
numarul submultimilor lui ![]() este
este ![]() ;
;
numarul submultimilor
nevide
ale lui ![]() este
este ![]() ;
;
numarul submultimilor cu ![]() elemente, unde
elemente, unde ![]() , ale lui
, ale lui ![]() este
este ![]() .
.
Fie ![]() ,
, ![]() o multime finita cu
o multime finita cu ![]() elemente si
elemente si ![]() o multime cu
o multime cu ![]() elemente. Atunci:
elemente. Atunci:
numarul functiilor definite pe ![]() cu valori in
cu valori in ![]() este
este ![]() ;
;
numarul functiilor
injective definite pe ![]() cu valori in
cu valori in ![]() este
este ![]() , daca
, daca ![]() si 0 in rest;
si 0 in rest;
numarul functiilor
bijective definite pe ![]() cu valori in
cu valori in ![]() este
este ![]() , daca
, daca ![]() si 0 in rest.
si 0 in rest.
Probabilitatea unui eveniment
![]() .
.
Polinoame
Forma algebrica a polinomului ![]() in nedeterminata
in nedeterminata ![]() este:
este:
![]() , cu conventia
, cu conventia ![]() .
.
numerele ![]() se numesc coeficientii polinomului
se numesc coeficientii polinomului
notam cu:
1.
![]() multimea polinoamelor
cu coeficienti complecsi in nedeterminata
multimea polinoamelor
cu coeficienti complecsi in nedeterminata ![]()
2.
![]() multimea polinoamelor
cu coeficienti reali in nedeterminata
multimea polinoamelor
cu coeficienti reali in nedeterminata ![]()
3.
![]() multimea polinoamelor
cu coeficienti rationali in nedeterminata
multimea polinoamelor
cu coeficienti rationali in nedeterminata ![]()
4.
![]() multimea polinoamelor
cu coeficienti intregi in nedeterminata
multimea polinoamelor
cu coeficienti intregi in nedeterminata ![]()
se numeste gradul
polinomului ![]() si se noteaza
si se noteaza ![]() cel mai mare numar
natural
cel mai mare numar
natural ![]() cu proprietatea
cu proprietatea ![]() , gradul polinomului nul este prin conventie
, gradul polinomului nul este prin conventie ![]() .
.
fie ![]() ,
, ![]() si
si ![]() . Functia
. Functia ![]() ,
, ![]() ,
, ![]() se numeste functie polinomiala asociata
polinomului
se numeste functie polinomiala asociata
polinomului ![]() .
.
daca ![]() , atunci numarul
, atunci numarul ![]() se numeste valoarea polinomului
se numeste valoarea polinomului ![]() in
in ![]() .
.
numarul ![]() este radacina a polinomului
este radacina a polinomului ![]() daca
daca ![]() .
.
Fie
![]() doua polinoame,
doua polinoame, ![]() ,
, ![]() , atunci:
, atunci:
![]() ,
, ![]() , in paticular
, in paticular  ,
, ![]() .
.
![]() ;
; ![]() .
.
![]() ;
; ![]() cu egalitate daca
cu egalitate daca ![]() .
.
se numeste ecuatie
algebrica cu o necunoscuta, o ecuatie de forma ![]() , unde
, unde ![]() este un polinom nenul.
Gradul polinomului
este un polinom nenul.
Gradul polinomului ![]() se numeste gradul ecuatiei.
se numeste gradul ecuatiei.
fie ![]() ,
, ![]() si
si ![]() . Numarul
. Numarul ![]() se numeste radacina multipla de ordinul
se numeste radacina multipla de ordinul ![]() , daca
, daca ![]() divide
divide ![]() si
si ![]() nu divide
nu divide ![]() .
.
Observatie. Daca ![]() , atunci:
, atunci:
![]() (determinarea termenului liber)
(determinarea termenului liber)
![]() (determinarea sumei coeficientilor)
(determinarea sumei coeficientilor)
![]() (determinarea sumei
coeficientilor de rang par)
(determinarea sumei
coeficientilor de rang par)
![]() (determinarea sumei coeficientilor de rang impar).
(determinarea sumei coeficientilor de rang impar).
Teorema. (a impartirii cu rest) Fie ![]() ,
, ![]() . Atunci exista si sunt unice doua polinoame
. Atunci exista si sunt unice doua polinoame ![]() astfel incat
astfel incat ![]() cu
cu ![]() .
.
Teorema. (a restului) Fie ![]() si
si ![]() . Atunci restul impartirii lui
. Atunci restul impartirii lui ![]() prin
prin ![]() este
este ![]() .
.
Teorema. (a lui Bzout ) Fie ![]() ,
, ![]() . Numarul
. Numarul ![]() este radacina a polinomului
este radacina a polinomului
![]()
![]() divide
divide ![]() .
.
Teorema. Fie ![]() , cu
, cu ![]() ,
, ![]() . Daca
. Daca ![]() sunt radacinile lui
sunt radacinile lui ![]() , atunci
, atunci ![]() .
.
Teorema. (relatiile lui Viète) Numerele complexe ![]() sunt radacinile
polinomului
sunt radacinile
polinomului ![]() ,
, ![]() ,
, ![]() , daca si numai daca au loc relatiile :
, daca si numai daca au loc relatiile :
 .
.
Observatie. Particularizam pentru
cazurile in care gradul lui ![]() va fi 2, 3 sau 4.
va fi 2, 3 sau 4.
1. Daca ![]() ,
, ![]() , are radacinile
, are radacinile ![]() , atunci relatiile lui Viète sunt :
, atunci relatiile lui Viète sunt :
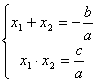 .
.
2. Daca ![]() ,
, ![]() , are radacinile
, are radacinile ![]() , atunci relatiile lui Viète sunt :
, atunci relatiile lui Viète sunt :
 .
.
3. Daca ![]() ,
, ![]() , are radacinile
, are radacinile ![]() , atunci relatiile lui Viète sunt:
, atunci relatiile lui Viète sunt:
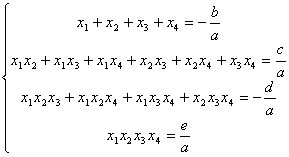 .
.
Observatie. Daca notam cu ![]() prima si respectiv a
doua relatie a lui Viète,
atunci suma patratelor radacinilor se obtine din
prima si respectiv a
doua relatie a lui Viète,
atunci suma patratelor radacinilor se obtine din ![]() .
.
Teorema. 1. Orice polinom nenul cu coeficienti reali, ![]() , daca admite radacina complexa
, daca admite radacina complexa ![]() , cu
, cu ![]() , atunci admite si radacina
, atunci admite si radacina ![]() si cele doua au
acelasi ordin de multiplicitate.
si cele doua au
acelasi ordin de multiplicitate.
2. Orice polinom nenul cu
coeficienti rationali, ![]() , daca admite radacina
, daca admite radacina ![]() , unde
, unde ![]() ,
, ![]() ,
, ![]() , atunci admite si radacina
, atunci admite si radacina ![]() si cele doua au
acelasi ordin de multiplicitate.
si cele doua au
acelasi ordin de multiplicitate.
3. Fie ![]() un polinom cu
coeficienti intregi, de grad
un polinom cu
coeficienti intregi, de grad ![]() . Daca
. Daca ![]() , unde
, unde ![]() este o radacina a lui
este o radacina a lui ![]() , atunci
, atunci ![]() si
si ![]() .
.
Consecinte. 1. Orice polinom cu coeficienti reali are un numar par de radacini complexe.
2. Orice polinom cu coeficienti reali de grad impar are cel putin o radacina reala.
3.
Daca polinomul ![]() admite radacina
admite radacina ![]() ,
, ![]() ,
, ![]() , atunci admite si radacinile
, atunci admite si radacinile ![]() ,
, ![]() ,
, ![]() .
.
4.
Daca polinomul ![]() admite radacina
intreaga
admite radacina
intreaga ![]() , atunci
, atunci ![]() este divizor al
termenului liber.
este divizor al
termenului liber.
Elemente de algebra liniara
Fie
![]() si
si ![]() ,
, ![]() . Se numeste matrice
de tipul
. Se numeste matrice
de tipul ![]() (cu m linii si n coloane) cu elemente din
(cu m linii si n coloane) cu elemente din ![]() , o functie
, o functie ![]() ,
, ![]() .
.
Observatie. 1. Notam matricele sub
forma:  .
.
2.
Daca ![]() , o matrice de tipul
, o matrice de tipul ![]() se numeste matrice linie; daca
se numeste matrice linie; daca ![]() , o matrice de tipul
, o matrice de tipul ![]() se numeste matrice coloana; daca
se numeste matrice coloana; daca ![]() , o matrice de tipul
, o matrice de tipul ![]() se numeste matrice patratica de ordinul
se numeste matrice patratica de ordinul ![]() .
.
3.
Se noteaza cu ![]() multimea tuturor
matricelor cu m linii si n coloane cu elemente din D. Daca multimea D este finita cu d
elemente, atunci numarul tuturor matricelor cu elemente din D este
multimea tuturor
matricelor cu m linii si n coloane cu elemente din D. Daca multimea D este finita cu d
elemente, atunci numarul tuturor matricelor cu elemente din D este ![]() .
.
4. Doua matrice sunt egale daca sunt de acelasi tip si elementele corespondente sunt egale.
5.
Daca ![]() este o matrice de
tipul
este o matrice de
tipul ![]() , atunci se numeste transpusa matricei
, atunci se numeste transpusa matricei ![]() , o matrice notata
, o matrice notata ![]() , de tipul
, de tipul ![]() , obtinuta din
, obtinuta din ![]() prin trasformarea
liniilor in coloane (si a coloanelor in linii).
prin trasformarea
liniilor in coloane (si a coloanelor in linii).
6.
Daca avem doua matrice ![]() de tipul
de tipul ![]() si
si ![]() de tipul
de tipul ![]() , atunci are sens produsul
, atunci are sens produsul ![]() si se va obtine o
matrice de tipul
si se va obtine o
matrice de tipul ![]() .
.
7. Inmultirea matricilor este asociativa.
Proprietati ale determinantilor
1. Determinantul unei matrice coincide cu determinantul matricei transpuse.
![]() .
.
2. Daca toate elementele unei linii (sau coloane) sunt nule, atunci determinantul matricei este nul.
3. Daca o matrice are doua linii (sau doua coloane) identice, atunci determinantul sau este nul.
4. Daca elementele a doua linii (sau doua coloane) ale unei matrice sunt proportionale, atunci determinantul este nul.
5.
Daca toate elementele unei linii (sau coloane) ale unei matrice sunt inmultite
cu un scalar ![]() , atunci obtinem o matrice al carei determinant este egal cu
determinantul matricei initiale inmultit cu
, atunci obtinem o matrice al carei determinant este egal cu
determinantul matricei initiale inmultit cu ![]() .
.
6. Daca intr-o matrice schimbam doua linii (sau doua coloane) intre ele obtinem o matrice care are determinantul egal cu opusul determinantului matricei initiale.
7. Daca la o linie (sau coloana)
a matricei ![]() adunam elementele
altei linii (sau coloane) inmultite cu acelasi scalar, atunci aceasta matrice
are acelasi determinant ca si matricea
adunam elementele
altei linii (sau coloane) inmultite cu acelasi scalar, atunci aceasta matrice
are acelasi determinant ca si matricea ![]() .
.
8. Daca o linie (sau o coloana) a unei matrice patratice este o combinatie liniara de celelalte linii
(sau coloane), atunci determinantul matricei este nul.
9.
Fie ![]() este o matrice
patratica de ordinul
este o matrice
patratica de ordinul ![]() . Presupunem ca elementele liniei
. Presupunem ca elementele liniei ![]() sunt de forma
sunt de forma ![]() . Daca
. Daca ![]() , respectiv
, respectiv ![]() , este matricea care se obtine din
, este matricea care se obtine din ![]() inlocuind elementele
de pe linia
inlocuind elementele
de pe linia ![]() cu
cu ![]() (respectiv
(respectiv ![]() )
) ![]() , atunci
, atunci ![]() .
.
 .
.
10.
![]() .
.
11.
![]() .
.
12.
Daca ![]() este o matrice
triunghiulara (sau diagonala), atunci determinantul este egal cu produsul
elementelor de pe diagonala principala.
este o matrice
triunghiulara (sau diagonala), atunci determinantul este egal cu produsul
elementelor de pe diagonala principala.

13. Determinantul produsului a doua matrici este egal cu produsul determinantilor acelor matrici.
![]() .
.
Consecinta:
![]()
Fie
![]() o matrice nenula.
Spunem ca matricea
o matrice nenula.
Spunem ca matricea ![]() are rangul
are rangul ![]() si scriem
si scriem ![]() , daca
, daca ![]() are un minor nenul de
ordin
are un minor nenul de
ordin ![]() si toti minorii de
ordin mai mare decat
si toti minorii de
ordin mai mare decat ![]() sunt nuli.
sunt nuli.
Fie
![]() o matrice patratica de
ordin
o matrice patratica de
ordin ![]() . Spunem ca
. Spunem ca ![]() este inversabila daca exista o matrice
este inversabila daca exista o matrice ![]() patratica de ordin
patratica de ordin ![]() astfel incat
astfel incat ![]() . Inversa matricei
. Inversa matricei ![]() , daca exista, se noteaza
, daca exista, se noteaza ![]() .
.
Observatie. O matrice ![]() patratica de ordinul n este inversabila daca si numai daca
patratica de ordinul n este inversabila daca si numai daca ![]() este inversabil, in
plus
este inversabil, in
plus ![]() .
.
Legi de compozitie. Structuri algebrice
Fie
![]() o multime nevida. O
aplicatie
o multime nevida. O
aplicatie ![]() definita pe produsul
cartezian
definita pe produsul
cartezian ![]() cu valori in
cu valori in ![]() ,
, ![]() ,
, ![]() se numeste lege de compozitie.
se numeste lege de compozitie.
Fie
![]() o multime finita,
o multime finita, ![]() . In acest caz o lege de compozitie
. In acest caz o lege de compozitie ![]() pe
pe ![]() ,
, ![]() , poate fi data prin ceea ce este cunoscut sub numele de
tabla operatiei
, poate fi data prin ceea ce este cunoscut sub numele de
tabla operatiei ![]() , care consta dintr-un tabel cu
, care consta dintr-un tabel cu ![]() linii si
linii si ![]() coloane afectate celor
coloane afectate celor
![]() elemente ale lui
elemente ale lui ![]() . Tabla legii de compozitie
. Tabla legii de compozitie ![]() contine la intersectia
liniei lui
contine la intersectia
liniei lui ![]() cu coloana lui
cu coloana lui ![]() , elementul
, elementul ![]() .
.
|
|
|
|
|
|
|
|
|
|
||
Fie
M o multime pe care este data o lege de compozitie ![]() . O submultime nevida
. O submultime nevida ![]() a lui
a lui ![]() cu proprietatea :
cu proprietatea : ![]() , se numeste parte
stabila a lui
, se numeste parte
stabila a lui ![]() in raport cu legea de
compozitie
in raport cu legea de
compozitie ![]() .
.
O
lege de compozitie ![]() ,
, ![]() , se numeste:
, se numeste:
asociativa, daca : ![]() .
.
comutativa, daca : ![]() .
.
Un
element ![]() se numeste element neutru pentru o lege de
compozitie
se numeste element neutru pentru o lege de
compozitie ![]() ,
, ![]() , daca :
, daca : ![]() .
.
Un
element ![]() se numeste simetrizabil in raport cu legea
de compozitie (asociativa si cu element neutru, fie acesta
se numeste simetrizabil in raport cu legea
de compozitie (asociativa si cu element neutru, fie acesta ![]() )
) ![]() ,
, ![]() , daca exista
, daca exista ![]() astfel incat :
astfel incat : ![]() .
.
O
multime nevida ![]() se numeste monoid in raport cu o lege de
compozitie definita pe
se numeste monoid in raport cu o lege de
compozitie definita pe ![]() ,
, ![]() ,
, ![]() , daca sunt satisfacute urmatoarele axiome :
, daca sunt satisfacute urmatoarele axiome :
![]()
![]() ;
;
![]()
![]() astfel incat
astfel incat ![]() ,
, ![]() .
.
Spunem
ca monoidul ![]() este comutativ (sau abelian) daca operatia acestuia
satisface si axioma :
este comutativ (sau abelian) daca operatia acestuia
satisface si axioma :
![]() .
.
Un
cuplu ![]() format cu o multime
nevida
format cu o multime
nevida ![]() si cu o lege de
compzitie pe
si cu o lege de
compzitie pe ![]() ,
, ![]() se numeste grup daca sunt satisfacute
urmatoarele axiome :
se numeste grup daca sunt satisfacute
urmatoarele axiome :

Observatie. 1. Un monoid ![]() cu proprietatea ca
orice element
cu proprietatea ca
orice element ![]() este simetrizabil (in
raport cu operatia acestuia) se numeste grup.
este simetrizabil (in
raport cu operatia acestuia) se numeste grup.
2.
Spunem ca cuplul ![]() este grup abelian sau grup comutativ, daca satisface si
axioma :
este grup abelian sau grup comutativ, daca satisface si
axioma :
![]() .
.
3.
Daca ![]() are un numar finit de
elemente
are un numar finit de
elemente ![]() , atunci spunem ca ordinul grupului g este n.
, atunci spunem ca ordinul grupului g este n.
Teorema. Intr-un grup ![]() sunt adevarate
regulile de simplificare la stanga si la dreapta :
sunt adevarate
regulile de simplificare la stanga si la dreapta :
![]()
si respectiv
![]() .
.
Teorema. Fie ![]() un grup. Oricare ar fi
un grup. Oricare ar fi
![]() , ecuatiile :
, ecuatiile :
![]() si
si ![]()
au
solutii unice in ![]() , anume
, anume ![]() , respectiv
, respectiv ![]() , unde
, unde ![]() este simetricul lui
este simetricul lui ![]() .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1622
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved