| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
CALCUL DIFERENTIAL PENTRU FUNCTII DE O VARIABILA REALA
Obiective : Insusirea de catre studenti a rolului derivatelor de ordinul intai si doi in studiul functiilor reale de o variabila reala si gasirea extremelor acesteia direct sau cu computerul.
Cuprins
Functii elementare si aplicatii
Rolul derivatelor de ordinul unu si doi in studiul functiilor de o variabila reala
Optimele functiilor de o variabila reala si aplicatii
Metode iterative de rezolvare a ecuatiilor
Rezumat
Intrebari
Bibliografie
Cuvinte-cheie : functie reala de o variabila reala ,derivate de ordin intai si doi , maximele
si minimele unei functii , metode iterative de rezolvarea unei ecuatii .
1 Functii elementare si aplicatii
O functie reala de
variabila reala definita pe ![]() cu valorile in
cu valorile in ![]() , este o corespondenta care asociaza fiecarui
element
, este o corespondenta care asociaza fiecarui
element ![]() , un element unic
, un element unic ![]() .
.
Daca x este factor sau sursa fizica (consum) sau sursa valorica (cheltuieli) iar y este productie fizica sau valorica (venit, profit, rata profit) atunci functia f se numeste functie de productie.
Cheltuielile pentru resurse sunt egale cu consumurile de resurse inmultite cu costurile resurselor iar venitul din produse este egal cu productia fizica inmultita cu pretul de vanzare al produselor. Cheltuielile au drept componente cheltuielile materiale, cele cu forta de munca si cele neproductive (taxe, impozite, TVA). Profitul este diferenta intre venituri si cheltuieli iar rata profitului este raportul intre profit si cheltuieli. Functii de productie concrete gasite din datele reale, sunt functiile de regresie din statistica.
Din definitia functiei
rezulta ca daca ![]() avem
avem ![]() si ca
si ca
f(A) = B .
Daca f(x1 ) = f(x2 ) implica x1 = x2 , functia f se numeste injectiva iar daca f(A) = B , functia se numeste surjectiva. O functie injectiva si surjectiva, se numeste bijectiva. O functie reala se precizeaza prin expresia analitica y = f(x) si multimile A, B sau prin tabel de valori:
|
X |
x |
xn |
|
|
Y |
y |
yn |
cu legea de
corespondenta ![]() si
si ![]() ,
, ![]() .
.
Orice functie se poate reprezenta grafic intr-un sistem de axe ortogonale printr-o curba
plana in
care orice paralela la 0x prin ![]() taie graficul lui f cel putin intr-un punct si
orice paralela la 0y prin
taie graficul lui f cel putin intr-un punct si
orice paralela la 0y prin ![]() , taie graficul lui f
exact intr-un punct. Daca functia f
este bijectiva, orice paralela la 0x prin
, taie graficul lui f
exact intr-un punct. Daca functia f
este bijectiva, orice paralela la 0x prin ![]() taie graficul lui f exact intr-un punct.
taie graficul lui f exact intr-un punct.
Clase de functii elementare
1.Functia
liniara ![]() ;
; ![]()
2.Functia
polinomiala ![]() ;
; ![]()
3.Functia
cat de polinoame ![]() ;
;
![]() ;
; ![]()
4.Functia
putere ![]() ;
; ![]()
5.Functia
exponentiala ![]() ;
; ![]() ,
, ![]()
6.Functia
logaritmica ![]() ,
, ![]() ,
, ![]()
Functiile trigonometrice directe:
a) ![]() , A=R ; B=[ -1; 1]
, A=R ; B=[ -1; 1]
b) ![]() , A=R ; B=[ -1; 1]
, A=R ; B=[ -1; 1]
c) ![]() ,
,  ; B=R
; B=R
8.Functiile trigonometrice inverse:
d) ![]() ,
, ![]() ;
; 
e) ![]() ,
, ![]() ;
; 
f) ![]() ,
, ![]() ;
; 
Functiile 1), 4) - 6), 8 d) - f) sunt bijective.
Teorema 1
1)Fie valorile lui x in pregresie aritmetica . Avem ![]() daca si
numai daca valorile lui y sunt
in progresie aritmetica.
daca si
numai daca valorile lui y sunt
in progresie aritmetica.
2)Fie valorile lui x in progresie geometrica. Avem ![]() daca si
numai daca valorile lui y sunt
in progresie geometrica.
daca si
numai daca valorile lui y sunt
in progresie geometrica.
3)Fie valorile lui x in progresie aritmetica. Avem ![]() daca si
numai daca valorile lui y sunt
in progresie geometrica.
daca si
numai daca valorile lui y sunt
in progresie geometrica.
4)Fie valorile lui x in progresie geometrica. Avem ![]() daca si
numai daca valorile lui y sunt
in progresie aritmetica.
daca si
numai daca valorile lui y sunt
in progresie aritmetica.
Demonstratie
1)Fie valorile lui x in progresie aritmetica: ![]()
Valorile lui ![]() sunt tot in progresie
aritmetica:
sunt tot in progresie
aritmetica: ![]() ,
, 
Reciproc, daca valorile lui
y sunt in progresie aritmetica: ![]() pentru a avea
pentru a avea ![]() pentru orice n I N , trebuie ca
pentru orice n I N , trebuie ca ![]() de unde prin identificarea
coeficientilor lui n si a
termenilor liberi din ambii membri rezulta
de unde prin identificarea
coeficientilor lui n si a
termenilor liberi din ambii membri rezulta ![]() ;
; ![]()
2)Valorile lui x sunt in progresie geometrica daca si numai
daca valorile lui ![]() sunt in progresie
aritmetica. In adevar, daca avem
sunt in progresie
aritmetica. In adevar, daca avem ![]() atunci avem
atunci avem ![]()
Reciproc, daca avem ![]() atunci avem
atunci avem
![]()
![]() devine prin logaritmare
log y = B1 log x +B0 unde B0 =
log b0.
devine prin logaritmare
log y = B1 log x +B0 unde B0 =
log b0.
Daca valorile lui x sunt in progresie geometrica
atunci valorile lui ![]() sunt in progresie
aritmetica deci conform punctului 1) avem
sunt in progresie
aritmetica deci conform punctului 1) avem ![]() daca si
numai daca valorile lui
daca si
numai daca valorile lui ![]() sunt in progresie
aritmetica ceea ce se intampla daca si numai daca
valorile lui y sunt in progresie
geometrica.
sunt in progresie
aritmetica ceea ce se intampla daca si numai daca
valorile lui y sunt in progresie
geometrica.
3)![]() devine prin logaritmare
devine prin logaritmare ![]()
![]() unde B0 = log b0.
unde B0 = log b0.
Daca valorile lui x sunt in progresie aritmetica,
conform punctului 1) avem ![]()
![]() daca si numai daca valorile lui
daca si numai daca valorile lui
![]() sunt in progresie aritmetica si
aceasta se intampla daca si numai daca valorile lui y sunt in progresie geometrica.
sunt in progresie aritmetica si
aceasta se intampla daca si numai daca valorile lui y sunt in progresie geometrica.
4)![]() devine
devine ![]() unde
unde ![]()
Daca valorile lui x sunt in progresie geometrica
atunci valorile lui ![]() sunt in progresie
aritmetica deci conform punctului 1) avem
sunt in progresie
aritmetica deci conform punctului 1) avem ![]() daca si numai daca valorile lui
y sunt in progresie aritmetica.
daca si numai daca valorile lui
y sunt in progresie aritmetica.
In concluzie, transformarile progresiilor aritmetica si geometrica se fac cu ajutorul functiilor liniara, putere, exponentiala si logaritmica dupa schema:

Q.E.D.
Aplicatii ale functiilor elementare
A).Functia exponentiala negativa
Fie y0 = f(0) si P plafonul functiei .
1) y0 < P deci P este plafon superior pentru f(x)
Functia este :
![]()
Pentru b > e avem logistica , crescatoare de la y0 la P , cu punctul de inflexiune
xi = ( ln b ) / a si cu graficul :

Pentru b≤ e avem curba de saturatie ,crescatoare de la y0 la P si cu graficul :

2) y0 > P deci P este plafon inferior pentru f(x)
Functia este :
![]()
Pentru b > e avem logistica , descrescatoare de la y0 la P , cu punctul de inflexiune
xi = ( ln b ) / a si cu graficul :

Pentru b ≤ e avem curba de saturatie , descrescatoare de la y0 la P si cu graficul :

B). Functia de concentrare/diluare
1)Functia de concentrare este y = y0 + x a .e- bx unde y0 = f(0) .
Ea are punctul de maxim x0 = b / a si punctele de inflexiune :

Graficul are forma :

2) Functia de diluare este y = y0 - x a .e- bx unde y0 = f(0) .
Ea are punctul de maxim x0 = b / a si punctele de inflexiune :

Graficul are forma :

C). Functia seismica asimetrica

Parametrii din expresiile precedente au semnificatia urmatoare :
a = momentul mijlocului undei maxime absolute (separa unda ascendenta de cea descendenta) ;
b = momentul incetarii undei ;
h = numarul de maxime ale undei ascendente ;
k = numarul de minime ale undei descendente ;
x1 = ((4h-3) / (4h-2)).a este punctul de maxim absolut al undei iar valoarea maxima absoluta este M ;
x2 = ((4k-1) / (4k-2)).a este punctul de minim absolut al undei iar valoarea minima absoluta este M ;
r = parametru de unda ( r > 1) ;
De exemplu pentru h = 2 si k = 3 avem graficul :

4)Calculul concentratiei pe termen lung
In administrarea ingrasamintelor, ierbicidelor, insecticidelor, vaccinurilor, etc., concentratia acestora se calculeaza astfel: vom presupune ca materialele precedente se administreaza in doze egale cu d la intervale de timp egale cu x.

Avem ![]() ;
;  deci dupa un
numar mare de administrari ale dozei constante d la intervale de timp egale cu x,
concentratia apartine intervalului:
deci dupa un
numar mare de administrari ale dozei constante d la intervale de timp egale cu x,
concentratia apartine intervalului:
 de lungime d.
de lungime d.
Grafic, valorile concentratiei y in raport cu lungimea x a intervalului de timp intre doua administrari succesive, sunt cuprinse in aria hasurata de inaltimea d:

Exemplu
Un ierbicid se administreaza in
doze constante egale cu ![]() la intervale de timp
egale cu
la intervale de timp
egale cu ![]() luni. Sa se afle
intervalul de variatie al concentratiei ierbicidului dupa un
numar mare de administrari.
luni. Sa se afle
intervalul de variatie al concentratiei ierbicidului dupa un
numar mare de administrari.
Solutie
Pentru ![]() ;
; ![]() avem:
avem:
![]()
![]()
5)Calculul dobanzilor
a)Dobanda simpla
Fie ![]() suma imprumutata
de la banca si care trebuie restituita in x ani cu dobanda anuala
suma imprumutata
de la banca si care trebuie restituita in x ani cu dobanda anuala ![]() . Suma imprumutata
. Suma imprumutata ![]() este rambursata
in x ani in rate anuale de y0 / x lei.La aceste rate se adauga dobanzile anuale in lei pentru
debitele existente in anul respectiv.
este rambursata
in x ani in rate anuale de y0 / x lei.La aceste rate se adauga dobanzile anuale in lei pentru
debitele existente in anul respectiv.
In primul an debitul este ![]() lei deci dobanda este
lei deci dobanda este ![]() lei.
lei.
In al x - lea an, debitul este  lei deci dobanda este
lei deci dobanda este ![]() lei.
lei.
Dobanda totala in x ani in lei va fi:

Dobanda anuala pe x ani in procente este ![]()
![]() deci o functie
liniara de x.
deci o functie
liniara de x.
Suma
totala ce se restituie in X ani este: ![]() . Dobanda D ajunge egala cu P
. Dobanda D ajunge egala cu P ![]() daca rambursarea
se face in
daca rambursarea
se face in ![]() ani.
ani.
Exemplu
O asociatie agricola
imprumuta de la Banca Agricola suma de y0 = 12000 lei,
care vor fi rambursati in ![]() ani cu dobanda
anuala
ani cu dobanda
anuala ![]() . Se cere dobanda totala D
. Se cere dobanda totala D ![]() si suma
totala y ce trebuie
restituita in
si suma
totala y ce trebuie
restituita in ![]() ani. In cati ani
avem
ani. In cati ani
avem ![]() ?
?
Solutie
![]() de unde
de unde ![]()
![]() de unde y = 15300 lei.
de unde y = 15300 lei.
![]() in
in ![]() ani
ani
b) Dobanda compusa
Fie ![]() suma depusa la
banca in momentul zero pentru care de adauga dobanda anuala d
suma depusa la
banca in momentul zero pentru care de adauga dobanda anuala d ![]() .
.
In primul an,
depozitul este ![]() deci valoarea dobanzii
este
deci valoarea dobanzii
este ![]() lei.
lei.
In al doilea an, depozitul este ![]() deci valoarea dobanzii
este
deci valoarea dobanzii
este ![]() lei.
lei.
In al x
- lea an, depozitul este ![]() deci valoarea dobanzii
este
deci valoarea dobanzii
este ![]() lei.
lei.
Dobanda totala pe x ani in lei va fi:

Dobanda totala pe x ani in procente este:![]() adica o functie exponentiala de x.
adica o functie exponentiala de x.
Suma totala acumulata
dupa x ani este: ![]()
Dobanda ajunge egala cu P ![]() dupa trecerea a
dupa trecerea a  ani
ani
Exemplu
Un fermier depune la banca anual
suma y0 = 500 lei pentru care se acorda dobanda anuala ![]() . Se cere dobanda totala D
. Se cere dobanda totala D ![]() si suma
totala acumulata y
dupa
si suma
totala acumulata y
dupa ![]() ani. In cati ani
avem
ani. In cati ani
avem ![]() ?
?
Solutie
Avem ![]() de unde
de unde ![]()
Avem ![]() de unde y = 815 lei
de unde y = 815 lei
![]() in
in  ani
ani
6).Evaluarea numarului de fructe pe pom
Date necesare:
NF = Numarul de flori pe pom = 2542
qF = Proportia de flori viabile = 0.9
S = Numarul de ovule pe floare = 10
q = Proportia de ovule fertile pe floare = 0.6
m = Numarul de vizite ale insectelor pe ora si pe floare = 0.4
q = Probabilitatea ca o vizita de insecta sa fecundeze un ovul dat intr-o floare = 0.1
Parametrii perioadei
de polenizare efectiva: ![]() si
si ![]()
![]() = viteza de
cadere a fructelor cu k
seminte
= viteza de
cadere a fructelor cu k
seminte ![]()
![]() = factor de stress =
0.99
= factor de stress =
0.99
Rezultate
1)Numarul de fructe cu k seminte pe pom la momentul zero este:

2)Numarul de fructe cu zero seminte pe pom la momentul zero este:

3)Numarul de fructe cu k seminte pe pom la momentul t este:

4)Numarul de fructe total pe pom
la momentul t este: ![]()
Diferenta intre numarul de fructe pe pom la momentele 0 si t este numarul de fructe cazute din pom (cu sau fara seminte).
2 Rolul derivatelor de ordinul unu si doi in studiul functiilor de o variabila reala
Fie functia reala de o
variabila reala ![]() ,
, ![]() si fie
si fie ![]() .
.
Numarul real L este limita
functiei f in x0 (Notatie ![]() ) daca pentru orice
) daca pentru orice ![]() exista
exista ![]() astfel ca
daca
astfel ca
daca ![]() sa avem
sa avem ![]()
Pentru ca f sa aiba limita L in ![]() , trebuie ca L sa existe, sa fie
unica si finita.
, trebuie ca L sa existe, sa fie
unica si finita.
O definitie echivalenta
pentru limita este: ![]() daca pentru orice
sir de numere reale
daca pentru orice
sir de numere reale ![]() cu
cu ![]() , sa avem sirul de numere reale
, sa avem sirul de numere reale ![]() convergent catre
convergent catre ![]() . Limita L a functiei f in
. Limita L a functiei f in ![]() exista, este
finita si unica daca si numai daca limitele
laterale
exista, este
finita si unica daca si numai daca limitele
laterale  ,
,  exista, sunt
finite si egale.
exista, sunt
finite si egale.
Proprietati ale functiilor reale
Functia reala f este continua in ![]() daca exista,
este unica si finita
daca exista,
este unica si finita ![]() si in plus
si in plus ![]() .
.
Functia reala f este derivabila in ![]() daca exista,
este unica si finita limita:
daca exista,
este unica si finita limita:
![]()
![]() se numeste valoarea
derivatei
se numeste valoarea
derivatei ![]() a functiei f(x)
in x0 si este
egala cu panta tangentei in
a functiei f(x)
in x0 si este
egala cu panta tangentei in ![]() la graficul lui f :
la graficul lui f : ![]()

Ecuatia
acestei tangente este: ![]()
Corespondenta
![]() defineste o
noua functie
defineste o
noua functie ![]() cu
cu ![]() , numita derivata intai a functiei f. Marimea
, numita derivata intai a functiei f. Marimea ![]() se numeste diferentiala
de ordinul intai a lui f in x0.
se numeste diferentiala
de ordinul intai a lui f in x0.
Derivata
derivatei intaia se numeste derivata a doua a functiei ![]() .
.
Marimea ![]() se numeste diferentiala
de ordinul doi a functiei f.
se numeste diferentiala
de ordinul doi a functiei f.
Mai general, derivata de ordin n a lui f se defineste inductiv ![]() .
.
![]() este cresterea
valorica a variabilei x iar Dx / x0 este cresterea procentuala a
variabilei x.
este cresterea
valorica a variabilei x iar Dx / x0 este cresterea procentuala a
variabilei x.
![]() este cresterea
valorica a functiei
este cresterea
valorica a functiei ![]() iar Dy / y0 este cresterea procentuala a
functiei
iar Dy / y0 este cresterea procentuala a
functiei ![]() .
.
![]() este derivata
valorica in timp ce
este derivata
valorica in timp ce  este derivata
procentuala si se numeste elasticitatea functiei f in x0.
Avem
este derivata
procentuala si se numeste elasticitatea functiei f in x0.
Avem 
Fie ![]() . Conform teoremei Lagrange, exista
. Conform teoremei Lagrange, exista ![]() astfel ca
astfel ca ![]() si deci
si deci ![]() .
.

In adevar, M2 este
intersectia graficului cu coarda M1M2 paralela
cu tangenta M0T iar ![]() este abcisa lui M2.
In concluzie, derivata instantanee
este abcisa lui M2.
In concluzie, derivata instantanee ![]() este egala cu
derivata medie
este egala cu
derivata medie ![]() iar elasticitatea
instantanee
iar elasticitatea
instantanee ![]() este egala cu
elasticitatea medie
este egala cu
elasticitatea medie ![]() calculate pe un
interval convenabil ales
calculate pe un
interval convenabil ales ![]() care contine pe
care contine pe ![]() .
.
Formule de derivare pentru functii elementare
1. ![]()
2. ( xa ) = axa-1 (aIR)
3. (ax) = ![]() ; (ex) = ex
; (ex) = ex
![]() ;
; ![]()
![]()
![]()
![]()


![]()
Formule de derivare in operatii cu functii
I. ![]()
II. ![]()
III. 
Formulele 1. - 10. si I. - III. le admitem fara demonstratie.
Derivata logaritmica a functiei f in x0 este fL'(x0) , data de relatia :

Exemple
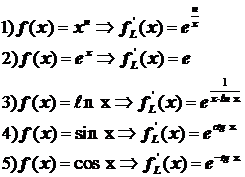
3)Functia reala f este crescatoare pe ![]() daca pentru orice
daca pentru orice
![]() cu
cu ![]() rezulta
rezulta ![]() . In mod analog se defineste functia descrescatoare
pe
. In mod analog se defineste functia descrescatoare
pe ![]() :
: ![]() . O functie reala care este fie crescatoare
fie descrescatoare pe A se numeste functie monotona pe A.
. O functie reala care este fie crescatoare
fie descrescatoare pe A se numeste functie monotona pe A.
Functia reala f este convexa pe ![]() daca pentru orice
daca pentru orice
![]() cu
cu ![]() rezulta
rezulta ![]() . Graficul unei functiei convexe pe A are deschiderea in
directia pozitiva a axei 0y
iar coarda care uneste doua puncte ale graficului, este deasupra
graficului:
. Graficul unei functiei convexe pe A are deschiderea in
directia pozitiva a axei 0y
iar coarda care uneste doua puncte ale graficului, este deasupra
graficului:
|
|
|
O definitie echivalenta a
convexitatii este: pentru orice ![]() si orice
si orice ![]() avem
avem ![]() adica ordonata
tangentei in
adica ordonata
tangentei in ![]() la graficul lui f este sub acest grafic:
la graficul lui f este sub acest grafic:
|
|
|
In mod asemanator se
defineste functia concava pe A: ![]() respectiv
respectiv ![]()
Functia reala f este marginita pe A
daca exista m, M I R astfel ca ![]() pentru orice
pentru orice ![]() .
.
Functia reala f este periodica pe A
daca exista ![]() astfel ca
astfel ca ![]() pentru orice
pentru orice ![]() .
.
Exemple
Functiile ![]() ,
, ![]() sunt periodice cu
perioada
sunt periodice cu
perioada ![]() iar functia
iar functia ![]() este periodica cu
perioada
este periodica cu
perioada ![]()
Fie ![]() ,
, ![]() ,
, ![]() .
.
Rolul derivatelor de ordin I si II in studiul functiei reale f, este dat de:
Teorema 2
1)Daca ![]() pe intervalul
pe intervalul ![]() atunci
atunci ![]() este crescatoare
pe intervalul
este crescatoare
pe intervalul ![]() . Daca
. Daca ![]() pe intervalul
pe intervalul ![]() atunci
atunci ![]() este
descrescatoare pe intervalul
este
descrescatoare pe intervalul ![]() .
.
2)Daca ![]() pe intervalul
pe intervalul ![]() atunci
atunci ![]() este convexa pe
intervalul
este convexa pe
intervalul ![]() . Daca
. Daca ![]() pe intervalul
pe intervalul ![]() atunci
atunci ![]() este concava pe
intervalul
este concava pe
intervalul ![]() .
.
Demonstratie
Daca f este functie cu derivate de toate ordinele continue pe
intervalul ![]() atunci pentru orice
atunci pentru orice ![]() avem formula Taylor
(fara demonstratie):
avem formula Taylor
(fara demonstratie):
![]() unde
unde  .
.
1)Avem formula Taylor pentru ![]() :
:  cu
cu  . Pentru x
suficient de aproape de
. Pentru x
suficient de aproape de ![]() , ultimul termen din membrul II este neglijabil
fata de cei precedenti deci
, ultimul termen din membrul II este neglijabil
fata de cei precedenti deci ![]() si
si  au acelasi semn.
Daca
au acelasi semn.
Daca ![]() atunci
atunci ![]() implica
implica ![]() deci f este crescatoare pe
deci f este crescatoare pe ![]() .
.
2)Avem formula Taylor pentru ![]() :
:  cu
cu  .
.
Pentru x suficient de aproape de ![]() , ultimul termen din membrul doi este neglijabil
fata de cei precedenti, deci
, ultimul termen din membrul doi este neglijabil
fata de cei precedenti, deci  si
si  au acelasi semn.
au acelasi semn.
Daca ![]() atunci
atunci ![]() implica
implica 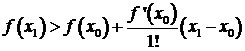 deci f este convexa pe
deci f este convexa pe ![]() . Daca
. Daca ![]() atunci
atunci ![]() implica
implica  deci f este concava pe
deci f este concava pe ![]() .Q.E.D.
.Q.E.D.
3 Optimele functiilor monofactoriale si aplicatii
Functia reala f:A R B R are un maxim relativ (local) in ![]() daca pentru orice
daca pentru orice
![]() avem
avem ![]() si pentru orice
si pentru orice ![]() avem
avem ![]() , deci pe intervalul
, deci pe intervalul ![]() valoarea
valoarea ![]() este cea mai mare.
este cea mai mare.
Functia
reala f:A R B R are un minim
relativ (local) in ![]() daca pentru orice
daca pentru orice
![]() avem
avem ![]() si pentru orice
si pentru orice ![]() avem
avem ![]() , deci pe intervalul
, deci pe intervalul ![]() valoarea
valoarea ![]() este cea mai
mica.
este cea mai
mica.
Punctele de maxim sau minim relative (local) se numesc cu un cuvant puncte de extreme relative (locale).
Daca functia f are cel putin un maxim relativ, cel mai mare maxim relativ se numeste maxim absolut (global).
Daca functia f are cel putin un minim relativ, cel mai mic minim relativ se numeste minim absolut (global).
Teorema 3 (Fermat)
Fie functia f:A R B R si ![]() . Daca f este
derivabila in
. Daca f este
derivabila in ![]() si
si ![]() este punct de maxim
sau minim relativ, atunci
este punct de maxim
sau minim relativ, atunci ![]() .
.
Demonstratie
Fie de exemplu ![]() = punct de maxim
relativ. Pentru
= punct de maxim
relativ. Pentru ![]() avem
avem ![]() deci
deci  si la limita
pentru
si la limita
pentru ![]() avem
avem ![]() . Pentru
. Pentru ![]() avem
avem ![]() deci
deci  si la limita
pentru
si la limita
pentru ![]() avem
avem ![]() . Rezulta
. Rezulta ![]() .Q.E.D.
.Q.E.D.
Punctele ![]() cu
cu ![]() se numesc puncte
stationare pentru ca in aceste puncte tangenta la grafic este
orizontala (valorile functiei stationeaza in
se numesc puncte
stationare pentru ca in aceste puncte tangenta la grafic este
orizontala (valorile functiei stationeaza in ![]() avand viteza de
variatie
avand viteza de
variatie ![]() nula).
nula).
Conditia din teorema 3 este
necesara dar nu suficienta pentru puncte de maxim sau minim
relativ, adica nu orice punct stationar este punct de maxim sau minim
relativ. Conform teoremei 2, ![]() este punct de maxim
relativ daca
este punct de maxim
relativ daca ![]() si in plus
si in plus ![]() deci
deci ![]() = crescatoare
pentru
= crescatoare
pentru ![]() iar
iar ![]() deci
deci ![]() = descrescatoare
pentru
= descrescatoare
pentru ![]() .
.
Deasemenea ![]() este punct de minim relativ daca
este punct de minim relativ daca ![]() si in plus
si in plus ![]() deci
deci ![]() = descrescatoare
pentru
= descrescatoare
pentru ![]() si
si ![]() deci
deci ![]() = crescatoare
pentru
= crescatoare
pentru ![]() .
.
Daca ![]() dar
dar ![]() pentru orice
pentru orice ![]() respectiv
respectiv ![]() pentru orice
pentru orice ![]() atunci
atunci ![]() este punct de
inflexiune cu tangenta orizontala. O conditie suficienta de
maxim sau minim relativ este data de:
este punct de
inflexiune cu tangenta orizontala. O conditie suficienta de
maxim sau minim relativ este data de:
Fie functia reala f cu derivate continue de toate ordinele
in ![]() si cu
si cu ![]() . Fie numarul natural minim
. Fie numarul natural minim ![]() , astfel ca
, astfel ca ![]() dar
dar ![]() . Daca k este
numar par, avem situatiile:
. Daca k este
numar par, avem situatiile:
a) ![]() in care caz
in care caz ![]() este punct de minim
relativ.
este punct de minim
relativ.
b) ![]() in care caz
in care caz ![]() este punct de maxim
relativ.
este punct de maxim
relativ.
Daca k este numar impar, ![]() este punct de
inflexiune cu tangenta orizontala.
este punct de
inflexiune cu tangenta orizontala.
Demonstratie
In conditiile din enunt,
formula Taylor devine:  cu
cu  . Pentru x
suficient de aproape de
. Pentru x
suficient de aproape de ![]() , ultimul termen din membrul doi se poate neglija in raport
cu primul termen. Daca k este numar
par,
, ultimul termen din membrul doi se poate neglija in raport
cu primul termen. Daca k este numar
par, ![]() si
si ![]() au acelasi semn
si avem subcazurile:
au acelasi semn
si avem subcazurile:
a) ![]() pentru orice
pentru orice ![]() deci si
deci si ![]() pentru orice
pentru orice ![]() adica
adica ![]() este punct de minim
relativ.
este punct de minim
relativ.
b) ![]() pentru orice
pentru orice ![]() deci si
deci si ![]() pentru orice
pentru orice ![]() adica
adica ![]() este punct de maxim
relativ.
este punct de maxim
relativ.
Daca k este numar impar, fie de exemplu ![]() deci
deci ![]() si
si ![]() au acelasi semn.
au acelasi semn.
Daca ![]() avem
avem ![]() iar daca
iar daca ![]() avem
avem ![]() deci
deci ![]() este punct de
inflexiune cu tangenta orizontala caci
este punct de
inflexiune cu tangenta orizontala caci ![]() .Q.E.D.
.Q.E.D.
Exemple
Sa se calculeze unghiul optim de
ramificatie intre doua vase sanguine de raze ![]() si
si ![]() .
.
Solutie
Vasul sanguin AD are raza
sectiunii ![]() iar vasul sanguin DC
are raza sectiunii
iar vasul sanguin DC
are raza sectiunii ![]() .
.

Rezistenta la inaintarea sangelui este direct proportionala cu lungimea vasului si invers proportionala cu raza sectiunii sale.
Rezistenta totala a
portiunii ![]() va fi:
va fi:  unde k este o constanta care depinde de
vascozitatea si densitatea sangelui.
unde k este o constanta care depinde de
vascozitatea si densitatea sangelui.
Avem ![]() ;
; ![]() cosec x deci
cosec x deci 
 are solutia
are solutia  . Avem
. Avem ![]() deci
deci ![]() este punct de minim.
Valoarea minimului este
este punct de minim.
Valoarea minimului este ![]() . De exemplu pentru
. De exemplu pentru ![]() avem
avem ![]() .
.
La ce inaltime trebuie plasata o sursa de lumina intr-o baterie pentru pasari astfel ca intensitatea iluminarii pardoselii sa fie maxima?
Solutie
Fie A punctul cel mai departat al pardoselii de verticala sursei luminoase SN.
Fie ![]() ;
; ![]() ;
; ![]() . Intensitatea luminoasa in punctul A este
. Intensitatea luminoasa in punctul A este ![]() .
.

Avem ![]() si
si  deci:
deci:  .
.
Avem  cu radacina
cu radacina  deci
deci ![]()
Avem ![]() deci
deci ![]() este punct de maxim.
Valoarea maximului este
este punct de maxim.
Valoarea maximului este 
Sa se confectioneze o adapatoare de beton cu sectiune trapezoidala astfel ca volumul adapatorii sa fie maxim.
Solutie
Lungimea adapatorii fiind constanta, trebuie sa maximizam aria sectiunii.

Baza mica a sectiunii este a, cea mare este ![]() iar
inaltimea sectiunii este
iar
inaltimea sectiunii este ![]() deci aria trapezului
va fi:
deci aria trapezului
va fi: ![]()
 are radacina
pozitiva
are radacina
pozitiva  . Avem
. Avem ![]() deci
deci ![]() este punct de maxim.
Valoarea maximului este
este punct de maxim.
Valoarea maximului este ![]() .
.
Cazuri particulare
a) ![]() deci
deci ![]() asa ca
asa ca ![]()
b) ![]() deci
deci  asa ca
asa ca ![]()
Sa se dimensioneze un canal trapezoidal deschis pentru irigatii astfel ca, costul saparii lui sa fie minim.
Solutie
Fie raportul ![]() intre
latimea fundului canalului a
si adancimea canalului h.
intre
latimea fundului canalului a
si adancimea canalului h.

Costul sapaturii canalului este direct proportional cu aria sectiunii deoarece lungimea canalului si costul sapaturii (lei / m3) este constanta.
Trebuie sa minimizam aria sectiunii in raport cu x astfel ca pe canal sa fie asigurat un debit Q dat de apa. Fie m = tg a panta taluzului
Aria sectiunii este: ![]() . Dar
. Dar ![]() deci
deci ![]()
h se determina cu conditia sa se asigure pe canal debitul Q, panta fundului canalului este i iar n este rugozitatea peretilor si fundului canalului la curgerea apei
(n = 0.025 pentru canale de pamant si n = 0.014 pentru canale dalate cu beton).
Avem relatia: 
Rezulta: ![]() unde
unde  este o constanta
hidraulica a canalului. Trebuie sa avem:
este o constanta
hidraulica a canalului. Trebuie sa avem: ![]() adica:
adica:

deci dupa efectuarea calculelor obtinem:
![]() cu punctul de minim:
cu punctul de minim:
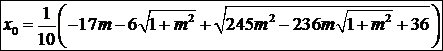
In locul minimizarii volumului sapaturii se mai pot minimiza:
a) costul apei pierdute prin infiltratii pe fundul si peretii canalului;
b) profitul pierdut anual de pe suprafata scoasa din circuitul agricol de catre canal.
Dintr-o foaie dreptunghiulara din fier sau carton cu lungimea a si latimea b se taie in fiecare colt cate un patrat de latura x iar marginile ramase se indoaie, obtinand o cutie paralelipipedica fara capac de tip ladita de fructe. Sa se afle x astfel ca volumul cutiei sa fie maxim.
Solutie

Avem ![]() .
. ![]() are
radacina:
are
radacina:

Avem ![]() deci
deci ![]() este punct de maxim.
Valoarea maximului este
este punct de maxim.
Valoarea maximului este ![]() .
.
Pentru ![]() avem
avem  .
.
6) Optimizarea nivelului preturilor de vinzare sub aspectul maximizarii venitului din
vinzarea produselor agricole, a stimularii consumului de produse agricole ca o cale principala
de relansare a productiei agricole .
Fie x pretul de vinzare variabil (lei / Kg) al unui produs agricol , fie y cantitatea variabila din podus , vanduta intr-un interval de timp de lungime T , la pretul de vanzare x si fie z =x.y valoarea variabila in lei a cantitatii vandute la pretul de vanzare x .
Fie xc pretul de vanzare curent al produsului , fie yc cantitatea vanduta
la pretul de vinzare curent xc si fie zc = xc.yc valoarea in lei a cantitatii vandute la pretul de vanzare
curent xc .
Fie xp un pret de vanzare de proba pentru testarea pietii , pentru care avem in acelasi interval de timp
de lungime T , cantitatea de produs vanduta yp si valoarea in lei a cantitatii vandute zp la pretul de
vanzare xp.
Este clar ca avem functia y = f(x) descrescatoare in raport cu x , datorita limitarii puterii de
cumparare a cumparatorilor potentiali .Avem z = x.f(x) .
Dorim sa calculam pretul de vanzare economic xe pentru care valoarea in lei a cantitatii
vandute ze = xe.f(xe) este maxima .
a) Cazul produselor de necesitate nespecificata
In acest caz cantitatea de produs y scade direct proportional odata cu cresterea pretului de vinzare
x , deci cantitatea de produs vanduta are forma y = a.x + 2.b cu a < 0 .
Coeficientii a , b se gasesc din conditiile :
yc = a.xc + 2.b ; yp = a.xp +2.b deci a = (yp - yc ) / (xp - xc) si b = (xp.yc - xc.yp) / 2.(xp - xc)
Avem z = x.y = a.x2 + 2.b.x deci z = maxim pentru z' = 2a.x + 2.b = 0 asa ca
xe = b / -a deci ye = b si ze = xe.ye = maxim .

Exemplu:
Un vanzator a vandut la piata cu pretul curent xc = 2.5 lei / Kg in T =10 ore o cantitate yc = 8 kg
fasole boabe pentru care a primit suma zc = 20 lei .
A doua zi a vandut la aceeasi piata cu pretul de proba xp = 3 lei tot in T = 10 ore o cantitate yp = 6 Kg fasole boabe pentru care a primit suma zp= 18 lei.Din formulele de mai sus rezulta pretul de vinzare economic xe = 2.25 lei /Kg cu care in T = 10 ore , s-ar vinde cantitatea ye = 9 Kg fasole boabe si s-ar primi suma maxima ze = 20.25 lei .
b) Cazul produselor de necesitate mare
In acest caz cantitatea de produs y scade lent odata cu cresterea pretului de vinzare x , deci cantitatea de produs vanduta are forma y = a.x2 + b cu a <0 .
Coeficientii a , b se gasesc din conditiile :
yc = a.xc2 + b ; yp = a.xp2 + b
Avem z = x.y = a.x3 + b.x deci z = maxim pentru z' = 3a.x2 + b = 0
asa ca xe = (b / ( - 3a))1 / 2 deci ye = 2b / 3 si ze = xe.ye = maxim .
Trebuie sa avem b / ( - 3a) > 0 si cum a < 0 , trebuie ca sa avem b >0 ,
conditie totdeauna indeplinita pentru ca functia f este descrescatoare .

Exemplu:
Un vanzator a vandut la piata cu pretul curent xc = 1 leu / Kg in T =10 ore o cantitate
yc = 60 kg cartofi pentru care a primit suma zc = 60 lei .
A doua zi a vandut la aceeasi piata cu pretul de proba xp = 1.2 lei tot in T = 10 ore o cantitate
yp = 50 Kg cartofi pentru care a primit suma zp= 60 lei..
Din formulele de mai sus rezulta pretul de vinzare economic xe = 1.1015 lei /Kg cu care in
T = 10 ore , s-ar vinde cantitatea ye = 55.15 Kg cartofi si s-ar primi suma maxima ze = 60.7502 lei .
c) Cazul produselor de necesitate mijlocie
In acest caz cantitatea de produs y scade mai intai lent apoi brusc odata cu cresterea pretului
de vinzare x , deci cantitatea de produs vanduta are forma y = 1 / (a.x2 + b ) cu punctul de inflexiune
xi = (b / 3a )1 /2
Coeficientii a , b se gasesc din conditiile :
1 / yc = a.xc2 + b ; 1 / yp = a.xp2 + b
Avem z = x.y = x / (a.x2 + b) deci z = maxim pentru z' = ( - a.x2 + b ) / (a.x2 + b )2 = 0 asa ca xe = (b / a)1 / 2 deci ye = 1 / 2b si ze = xe.ye = maxim .
Trebuie sa avem b / a > 0 de unde xp > xc.(yc / yp)1 / 2 .
Daca aceasta conditie nu este indeplinita , trebuie sa alegem alt xp .

Exemplu:
Un vanzator a vandut la piata cu pretul curent xc = 2 lei / Kg in T =10 ore o cantitate yc = 10 kg conopida pentru care a primit suma zc = 20 lei .
A doua zi a vandut la aceeasi piata cu pretul de proba xp = 2.5 lei / Kg , tot in T = 10 ore , o
cantitate yp = 8 Kg conopida pentru care a primit suma zp= 20 lei.
Conditia xp > xc.(yc / yp)1 / 2 este indeplinita .
Din formulele de mai sus rezulta pretul de vinzare economic xe = 2.2361 lei /Kg cu care in
T = 10 ore , s-ar vinde cantitatea ye = 9 Kg conopida si s-ar primi suma maxima ze = 20.1246 lei .
d) Cazul produselor de necesitate mica
In acest caz cantitatea de produs y scade brusc odata cu cresterea pretului de vinzare x , deci cantitatea de produs vanduta are forma y = 1 / (a.x + b )2
Coeficientii a , b se gasesc din conditiile :
1 / yc = (a.xc + b)2 ; 1 / yt = (a.xt + b)2
Avem z = x.y = x / (a.x + b)2 deci z = maxim pentru z' = (b - a.x) / (a.x+b)3
= 0 asa ca xe = b / a deci ye = 1 / 2b si ze = xe.ye = maxim .

Exemplu:
Un vanzator a vandut la piata cu pretul curent xc = 3 lei / Kg in T =10 ore o cantitate
yc = 10 kg capsuni pentru care a primit suma zc = 30 lei .
A doua zi a vandut la aceeasi piata cu pretul de proba xp = 4 lei / Kg , tot in T = 10 ore ,
o cantitate yp = 7 Kg capsuni pentru care a primit suma zp= 28 lei.
Din formulele de mai sus rezulta pretul de vinzare economic xe = 2.1222 lei /Kg cu care in
T = 10 ore , s-ar vinde cantitatea ye = 14.56 Kg capsuni si s-ar primi suma maxima ze = 30.9077 lei .
Programul PRET face aceste calcule .
7)Fie x = cheltuieli de productie si y = venitul anual la cultura porumbului (lei).
Avem ![]() deci profitul este
deci profitul este ![]() . Profitul este maxim daca
. Profitul este maxim daca ![]() deci
deci ![]() cu solutia
cu solutia ![]() si profitul maxim
si profitul maxim
![]() . Avem
. Avem ![]() deoarece
deoarece ![]() .
.
8) Inlocuirea optima a echipamentelor
Echipamentele sufera in timpul utilizarii uzura fizica deci necesita cheltuieli de intretinere si reparare.
Aparitia de echipamente noi provoaca uzura morala a celor vechi care trebuie inlocuite.
Momentul optim al inlocuirii echipamentelor vechi are ca scop minimizarea cheltuielilor medii de
intretinere si reparare luand in calcul si cheltuielile de cumparare si instalare si valoarea de recuperare prin revinzare sau casare(valorificarea materialelor refolosibile si reconditionarea pieselor vechi) a acestor echipamente .
A. Modele discrete de inlocuire optima a echipamentelor
Fie C0 cheltuielile de cumparare si instalare a unui echipament la momentul 0 si fie C1 ,., Cn
cheltuielile de intretinere si reparare a echipamentului la momentele de timp 1,., n .
Fie Vn valoarea de recuperare prin revanzare sau casare a echipamentului la momentul de timp n .
Cheltuielile medii pe perioada de timp 0 ; n sunt :
f(n) = ( C0 - Vn ) + (C1+.+Cn ) / n
care trebuie sa fie minime la momentul optim n0 cu f(n0 - 1) > f(n0) < f(n0 + 1) .
In cazul in care dorim actualizarea cheltuielilor , fie d rata dobanzii si d = 1 / (1+d) coeficientul de actualizare ( 0 < d < 1 ) .
In acst caz cheltuielile medii pe perioada de timp 0 ; n vor fi :
g(n) = ( C0 - dn. Vn ) + (C1+ d.C2 +.+d n - 1 .Cn ) / n
care trebuie sa fie minime la momentul optim n0 cu g(n0 - 1) > g(n0) < g(n0 + 1) .
Pentru d = 0 deci d = 1 reobtinem modelul fara actualizarea cheltuielilor .
Exemplu
Fie un echipament cu C0 = 50 unitati monetare si valorile descrescatoare V1,.,Vn si respectiv
crescatoare C1,.,Cn in aceleasi unitati monetare , date de tabelul urmator penztru n = 10 ani :
|
N | ||||||||||
|
Vn | ||||||||||
|
Cn |
a) Se cere momentul optim n0 al inlocuirii echipamentului fara actualizarea cheltuielilor ;
b) Se cere momentul optim n0 al inlocuirii echipamentului cu actualizarea cheltuielilor la o rata a dobanzii d = 5 % deci d
a) Calculele se exprima in tabelul de mai jos.
|
N |
Vn |
Cn |
C0 - Vn |
C1+.+Cn |
(C0 - Vn )+(C1+.+Cn) |
f(n) |
Avem n0 = 3 ani cu cheltuieli medii minime f(n0) = 14.33 unitati monetare .
b) Calculele se exprima in tabelul de mai jos .
|
N |
Vn |
Cn |
dn.Vn |
C0 - d n.Vn |
dn - 1.Cn |
C1+.+ d n - 1. Cn |
(C0 - Vn )+(C1+.+ d n - 1.Cn) |
f(n) |
|
|
Avem n0 = 3 ani cu cheltuieli medii minime actualizate f(n0) = 15.04 unitati monetare .
B. Modele continue de inlocuire optima a echipamentelor
Fie C0 cheltuielile de cumparare si punere in functiune a unui echipament la momentul de timp
t = 0
Fie a(t) functia de depreciere a echipamentului in intervalul de timp 0 ; t ; ea este o functie descrescatoare cu a(0) = 1 si a(t) 0 pentru t
Valoarea de recuperare prin revanzare sau casare a echipamentului va fi C0. a(t) .

Fie C(t) cheltuielile de intretinere si reparare a
echipamentului la momentul de timp t deci cheltuielile cumulate de
intretinere si reparare a
echipamentului in intervalul de timp 0 ; t vor fi
Avem β(0) = 0 si β(t) este crescatoare pe [0 ; +∞] .
Cheltuielile medii pe perioada de timp [0 ; t] sunt f(t) = / t care trebuie sa fie minime la momentul de timp t0 care este radacina pozitiva a ecuatiei f '(t) = 0 .
Deoarece f ''(t0 ) > 0 , t0 va fi valoare de minim a cheltuielilor medii f(t).Cheltuielile medii minime vor fi f0 = f(t0) .
In cazul in care dorim actualizarea cheltuielilor , fie d rata dobanzii si δ(t) = 1 / (1+d)t functia de actualizare a cheltuielilor .
In acest caz cheltuielile medii pe perioada de timp [0 ; t] vor fi :
g(t) = / t
care trebuie sa fie minime la momentul de timp t0 care este radacina pozitiva a ecuatiei g '(t) = 0 .
Deoarece f ''(t0 ) > 0 , t0 va fi valoare de minim a cheltuielilor medii actualizate g(t).
Cheltuielile medii minime vor fi f0 = f(t0) .
Pentru d = 0 deci δ = 0 reobtinem modelul continuu fara actualizarea cheltuielilor.
Exemplu
Fie un echipament cu α(t) = b / (at+b) care indeplineste conditiile a(0) = 1 si a(t) 0 pentru
t
Fie C(t) = C.t deci β(t) = C.t2 / 2 care verifica conditiile β(0) = 0 si β(t) este crescatoare pe
Avem f(t) = / t adica f(t) = (aC0) / ( at+b) + (C.t ) / 2 asa ca :
f '(t) = - (a2.C0 ) / (at+b)2 + C / 2 = 0 cu solutia pozitiva t0 = ( 2C0 / C) 1/2 - b / a .
Cum f ''(t0 ) > 0 , t0 este punct de minim al cheltuielilor medii f(t) . iar f0 = f(t0) sunt cheltuielile medii minime .
In cazul actualizarii cheltuielilor cu rata dobinzii d , avem functia de actualizare a cheltuielilor
δ(t) = 1 / (1+d)t deci cheltuielile medii au forma :

t0 va fi solutia
pozitiva a ecuatiei g'(t) = 0
. Cum g ''(t0) > 0 , t0
va fi punct de minim iar valoarea
cheltuielilor medii actualizate minime este g0 = g(t0) .
4 Metode iterative de rezolvare a ecuatiilor
Conform teoremei Fermat 3 punctele de
maxim sau minim ale unei functii ![]() se gasesc printre
radacinile ecuatiei
se gasesc printre
radacinile ecuatiei ![]() . Este deci necesara aflarea radacinilor reale
ale unei functii, adica a punctelor de intersectie ale
graficului functiei cu axa 0x.
. Este deci necesara aflarea radacinilor reale
ale unei functii, adica a punctelor de intersectie ale
graficului functiei cu axa 0x.
Daca functia este un polinom ![]() atunci ecuatia
atunci ecuatia ![]() se numeste ecuatie
algebrica. In caz contrar functia contine in expresia ei
alte functii elementare (
se numeste ecuatie
algebrica. In caz contrar functia contine in expresia ei
alte functii elementare (![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , etc.) si ecuatia se numeste transcendenta.
, etc.) si ecuatia se numeste transcendenta.
De cele mai multe ori ecuatiile de
forma ![]() nu au
radacini exacte (intregi sau rationale) ci radacini
aproximative.
nu au
radacini exacte (intregi sau rationale) ci radacini
aproximative.
Aceste radacini aproximative se afla prin metode iterative care vor fi prezentate in continuare.
Prima problema in rezolvarea
ecuatiilor ![]() prin metode iterative
este localizarea radacinilor reale adica
gasirea de intervale in care se gaseste cate o
radacina (simpla sau multipla).
prin metode iterative
este localizarea radacinilor reale adica
gasirea de intervale in care se gaseste cate o
radacina (simpla sau multipla).
O radacina ![]() a ecuatiei
a ecuatiei ![]() , este de multiplicitate m
2 daca
, este de multiplicitate m
2 daca ![]() dar
dar ![]() .
.
Prima etapa in localizarea
radacinilor reale ale ecuatiei ![]() este gasirea unui
interval care sa contina toate radacinile reale
ale ecuatiei. Pentru ecuatii polinomiale de forma:
este gasirea unui
interval care sa contina toate radacinile reale
ale ecuatiei. Pentru ecuatii polinomiale de forma: ![]() avem:
avem:
Teorema 5
Daca a este radacina reala a
lui ![]() si
si  , vom avea
, vom avea ![]()
Demonstratie
Impartind la nevoie ![]() cu
cu ![]() , putem presupune ecuatia de forma:
, putem presupune ecuatia de forma: ![]() cu
cu  .
.
a)Daca ![]() se poate arata
prin inductie ca
se poate arata
prin inductie ca ![]() pentru
pentru ![]() :
:
Fie ![]() ,
, ![]() ,
, ![]() .
.
Daca ![]() rezulta
rezulta ![]() pentru
pentru ![]() deci in final
deci in final  pentru
pentru ![]() .
.
b)Avem: ![]() de unde:
de unde: ![]()
Rezulta: ![]() deci polinomul:
deci polinomul: ![]() are proprietatea
are proprietatea ![]() .
.
Pe de alta parte ![]() pentru
pentru ![]() deci :
deci :  Q.E.D.
Q.E.D.
Localizarea propriu zisa a
radacinilor ecuatiei ![]() se poate face cu sirul
Rolle.
se poate face cu sirul
Rolle.
Conform teoremei lui Rolle, daca functia este derivabila pe R , intre doua radacini ale functiei se gaseste cel putin o radacina a derivatei sau cu alte cuvinte, intre doua radacini ale derivatei se gaseste cel mult o radacina a functiei (in cazul unei schimbari de semn a functiei pentru cele 2 radacini ale derivatei sale).
Deci daca cunoastem
radacinile ecuatiei ![]() putem localiza
radacinile ecuatiei
putem localiza
radacinile ecuatiei ![]() . Pentru ecuatii polinomiale avem:
. Pentru ecuatii polinomiale avem:

Aici ![]() sunt aranjamentele de n luate cate k:
sunt aranjamentele de n luate cate k: ![]()
Localizarea radacinilor ecuatiei polinomiale se va face astfel:
![]()
![]() are o
radacina reala cu care se localizeaza
radacinile lui
are o
radacina reala cu care se localizeaza
radacinile lui ![]() .
.
![]() are cel mult 2
radacini reale cu care se localizeaza radacinile lui
are cel mult 2
radacini reale cu care se localizeaza radacinile lui ![]() , etc.
, etc.
![]() are cel mult
are cel mult ![]() radacini
reale cu care se localizeaza radacinile lui
radacini
reale cu care se localizeaza radacinile lui ![]() .
.
Vom prezenta in continuare patru metode
iterative de rezolvare a ecuatiei ![]() , unde f este
continua pe
, unde f este
continua pe ![]() ,
, ![]() si exista o
singura radacina necunoscuta
si exista o
singura radacina necunoscuta ![]() .
.
I)Metoda bisectiei (injumatatirii)
1)Luam a0 =a; b0 = b; ![]()
2)Cunoscand pe an - 1 , bn - 1 , cn - 1 vom defini pe an, bn, cn astfel:
Daca ![]() luam an = cn - 1 ; bn
= bn - 1 si
luam an = cn - 1 ; bn
= bn - 1 si ![]() .
.
Daca ![]() luam an = an - 1 ; bn
= cn - 1 si.
luam an = an - 1 ; bn
= cn - 1 si. ![]()
Daca ![]() luam an = an - 1 ;
bn = bn - 1 si cn
= cn - 1 .
luam an = an - 1 ;
bn = bn - 1 si cn
= cn - 1 .
Sirul cn
tinde catre radacina necunoscuta unica ![]() a ecuatiei
a ecuatiei ![]() .
.
Eroarea antecalculata este ![]() deoarece
deoarece ![]()
Eroarea poscalculata este ![]() deoarece
deoarece ![]()
Eroarea de verificare este ![]()
Exemplu
Fie ecuatia ![]() pentru care se
stie ca exista si este unica radacina
pentru care se
stie ca exista si este unica radacina ![]() . Luam
. Luam ![]() iteratii deci avem radacina a c10 = 0.682129 (3
zecimale exacte)
iteratii deci avem radacina a c10 = 0.682129 (3
zecimale exacte)
![]() ;
; ![]() ;
; ![]()
Programul BISEC face aceste calcule.
II)Metoda coardei (secantei)
1)Luam a0 =a; b0 = b; 
2)Cunoscand pe an - 1 , bn - 1 , cn - 1 vom defini pe an, bn, cn astfel:
Daca ![]() luam an = cn - 1 ; bn
= bn - 1 si
luam an = cn - 1 ; bn
= bn - 1 si  .
.
Daca ![]() luam an = an - 1 ; bn
= cn - 1 si
luam an = an - 1 ; bn
= cn - 1 si  .
.
Daca ![]() luam an = an - 1 ; bn
= bn - 1 si cn
= cn - 1 .
luam an = an - 1 ; bn
= bn - 1 si cn
= cn - 1 .
Sirul cn tinde catre radacina necunoscuta
unica ![]() a ecuatiei
a ecuatiei ![]() .
.
a)Daca ![]() pe
pe ![]() atunci
atunci ![]() este crescatoare
pe
este crescatoare
pe ![]() si
si ![]() este convexa pe
este convexa pe ![]() . In acest caz eroarea antecalculata este:
. In acest caz eroarea antecalculata este:  caci
caci ![]() .
.
b)Daca ![]() pe
pe ![]() atunci
atunci ![]() este
descrescatoare pe
este
descrescatoare pe ![]() si
si ![]() este concava pe
este concava pe ![]() . In acest caz eroarea postcalculata este:
. In acest caz eroarea postcalculata este:  caci
caci ![]() .
.
Fie ![]() derivabila pe
derivabila pe ![]() si
si ![]() marginita pe
marginita pe
![]() :
: ![]() pentru orice
pentru orice ![]() . In acest caz eroarea poscalculata este:
. In acest caz eroarea poscalculata este:  caci avem:
caci avem: ![]() . Eroarea de verificare este
. Eroarea de verificare este ![]()
Exemplu
Fie ecuatia ![]() pentru care se
stie ca exista si este unica radacina
pentru care se
stie ca exista si este unica radacina ![]() . Avem
. Avem ![]() strict
descrescatoare pe
strict
descrescatoare pe ![]() iar
iar ![]() pe
pe ![]() .
.
![]() este
marginita pe
este
marginita pe ![]() si
si ![]() iar
iar ![]() . Luam
. Luam ![]() iteratii deci
avem radacina a c5
= 0.6821758 cu trei zecimale exacte. Pentru EA folosim relatia de la
punctul b) deci avem EA = 0.2373047
iteratii deci
avem radacina a c5
= 0.6821758 cu trei zecimale exacte. Pentru EA folosim relatia de la
punctul b) deci avem EA = 0.2373047
Deasemenea EP = 0.0001212 ;![]()
Programul SECAN face aceste calcule.
III)Metoda aproximatiilor succesive
Presupunem ca ecuatia ![]() are o
radacina reala unica
are o
radacina reala unica ![]() .
.
Scriem ecuatia sub forma: ![]() unde
unde ![]() ; g : [ c - r ; c + r } R .
; g : [ c - r ; c + r } R .
Radacina a a ecuatiei ![]() satisface relatia
satisface relatia
![]() adica a este punct fix al functiei g.
Radacina a se poate obtine ca limita a
sirului recurent
adica a este punct fix al functiei g.
Radacina a se poate obtine ca limita a
sirului recurent ![]() ,
, ![]() . Pentru ca sirul recurent
. Pentru ca sirul recurent ![]() sa fie
convergent, sunt suficiente doua conditii:
sa fie
convergent, sunt suficiente doua conditii:
Functia g trebuie sa fie contractie adica exista
![]() astfel ca pentru
orice
astfel ca pentru
orice ![]() sa avem:
sa avem:
![]()
a)Daca de exemplu ![]() este derivabila
pe
este derivabila
pe ![]() si derivata sa
si derivata sa ![]() are o margine
superioara subunitara
are o margine
superioara subunitara ![]() , atunci conform teoremei Lagrange, functia g este contractie.
, atunci conform teoremei Lagrange, functia g este contractie.
b)Deasemenea daca functia f :
[ c - r ; c + r ] R este monoton crescatoare iar
derivata ![]() este
marginita pe
este
marginita pe ![]() adica exista
adica exista
![]() cu
cu ![]() pentru orice
pentru orice ![]() , atunci pentru orice
, atunci pentru orice  functia
functia ![]() cu
cu ![]() este contractie.
este contractie.
Functia g trebuie sa indeplineasca conditia:
![]()
c)Aceasta conditie este
indeplinita de exemplu daca ![]() unde
unde ![]() este constanta de
contractie.
este constanta de
contractie.
d)In conditiile punctului 1) b),
daca ![]() atunci pentru orice
atunci pentru orice  contractia
contractia ![]() indeplineste
conditia (2).
indeplineste
conditia (2).
Teorema 6 (de punct fix)
Daca ![]() este contractie
pe
este contractie
pe ![]() cu constanta de
contractie
cu constanta de
contractie ![]() si
si ![]() este punctul fix unic
al lui g si in plus
este punctul fix unic
al lui g si in plus ![]() atunci sirul recurent
atunci sirul recurent
![]() cu
cu ![]() este convergent
catre a
este convergent
catre a
Demonstratie
Avem:
![]()
Dar ![]() asa ca
asa ca ![]() . Avem
. Avem ![]() cu
cu ![]() deci pentru
deci pentru ![]() conform criteriului
comparatiei (clestelui) rezulta
conform criteriului
comparatiei (clestelui) rezulta ![]() .Q.E.D.
.Q.E.D.
Eroarea antecalculata este:
![]() deoarece
deoarece ![]() .
.
Eroarea postcalculata este:
 deoarece
deoarece  .
.
Eroarea de verificare este ![]()
Exemplu
Fie ecuatia ![]() pentru care se
stie ca exista si este unica radacina
pentru care se
stie ca exista si este unica radacina ![]() . Fie
. Fie ![]() cu
cu ![]() .
.
Avem ![]()
In plus ![]() . Luam
. Luam ![]() iteratii deci
avem radacina a c30
= 0.7390823 cu 5 zecimale exacte. EA = 0.0056386; EP = 0.0000301; EV =
0.0000048
iteratii deci
avem radacina a c30
= 0.7390823 cu 5 zecimale exacte. EA = 0.0056386; EP = 0.0000301; EV =
0.0000048
Programul APROX face aceste calcule.
IV)Metoda tangentei (Newton)
Fie ecuatia ![]() care are radacina
unica
care are radacina
unica ![]() in intervalul
in intervalul ![]()
Presupunem ca ![]() este derivabila
de doua ori pe intervalul
este derivabila
de doua ori pe intervalul ![]() si ca
exista
si ca
exista ![]() astfel ca:
astfel ca:
![]()
![]()
pentru orice ![]() .
.
Fie sirul recurent  cu
cu ![]()
Teorema 7
Fie functia ![]() derivabila de
doua ori pe
derivabila de
doua ori pe ![]() si care satisface
relatiile (1), (2).
si care satisface
relatiile (1), (2).
Daca  atunci pentru orice
atunci pentru orice ![]() sirul recurent:
sirul recurent:  este convergent
catre a
este convergent
catre a
Demonstratie
Avem formula Taylor in punctul a
 cu
cu ![]() .
.
Rezulta:

Avem:

![]() conform
relatiilor (1) si (3)
conform
relatiilor (1) si (3)
Avem:
 .
.
Rezulta 
Dar ![]() deci
deci  pentru
pentru ![]() .Q.E.D.
.Q.E.D.
Pentru a alege valoarea initiala
x0 a sirului recurent
 vom proceda astfel:
fie f : [ p1 ; p2 ] R derivabila de doua ori pe
vom proceda astfel:
fie f : [ p1 ; p2 ] R derivabila de doua ori pe ![]() cu
cu ![]() si care satisface
conditiile (1), (2) pe intervalul
si care satisface
conditiile (1), (2) pe intervalul ![]() .
.
Prin metoda bisectiei putem ajunge
la un interval ![]() astfel ca
astfel ca ![]() si
si ![]() . In acest caz
. In acest caz ![]() asa ca
asa ca  si alegem:
si alegem:
![]()
Eroarea antecalculata
rezulta din demonstratia teoremei 7:  deoarece
deoarece ![]() .
.
Eroarea postcalculata este:
 deoarece
deoarece ![]() .
.
Eroarea de verificare este: ![]()
Exemplu
Fie ecuatia ![]() cu radacina
unica
cu radacina
unica ![]() .
.
Avem ![]() ;
; ![]() deci avem:
deci avem: ![]() ;
; ![]() ;
; ![]()
Prin metoda bisectiei gasim  cu
cu  si
si ![]()
Rezulta ![]() ;
; ![]() deci alegem
deci alegem  de exemplu
de exemplu ![]()
Sirul recurent are forma: 
Dupa ![]() iteratii
gasim radacina: a 0.6823719 cu 4 zecimale exacte.
iteratii
gasim radacina: a 0.6823719 cu 4 zecimale exacte.
Eroarea antecalculata este: EA = 0.0000153
Eroarea postcalculata este: EP = 0.0071547
Eroarea de verificare este: EV = 0.0001056
Programul TANG face aceste calcule.
Rezumat
In acest capitol se defineste functia reala de o variabila reala , se enumera proprietatile ei , se prezinta rolul derivatelor de ordinul unu si doi in studiul functiei , in special la gasirea maximelor
si minimelor functiei . Capitolul se incheie cu metodele iterative de rezolvare a ecuatiilor cu computerul.
Intrebari
Care este rolul derivatei de ordinul unu in studiul functiei de o variabila reala ?
Care este rolul derivatei de ordinul doi in studiul functiei de o variabila reala ?
Cum se gasesc maximele si minimele unei functii de o variabila reala ?
Ce aplicatii au in agricultura maximele si minimele unei functii de o variabila reala ?
Bibliografie
1. Stanasila O. " Analiza liniara si geometrie "Vol. I - II,Editura ALL ,2000 - 2001
2. Cenusa Gh. si col." Matematici pentru economisti " Editura CISON,2000
3. Cenusa Gh. si col." Matematici pentru economisti - culegere de probleme" Editura CISON,2000
4. Ene D. " Matematici (I) " Editura CERES , 2004
5. Gogonea S. , Ene D. " Analiza numerica " Editura Cartea Universitara , 2005
6. Ene D.,Gogonea S. "Metode numerice" Editura Cartea Universitara , 2005
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3021
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved