| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Indicii sunt marimi relative cu continut de marime medie prin care se calculeaza variatia in timp, in spatiu si in interiorul planului a aceluiasi indicator statistic
Indicii pot fi calculati izolat pentru un fenomen sau sub forma de sisteme de indici.
O prima grupare a indicilor se face dupa functia pe care o au in studiul variatiei fenomenelor social-economice. Dupa acest criteriu indicii se impart in trei grupe mari:
indici ai dinamicii;
indici teritoriali;
indici ai planificarii (programarii).
Indicii dinamicii sunt rezultatul compararii in timp a aceluiasi fenomen (y), deci in acest caz trebuie sa existe o perioada de baza notata cu yo si una sau mai multe perioade curente care se noteaza cu y1 sau cu y1, y2 ,,yn.
Indicii teritoriali sunt indicii care masoara variatia in spatiu a aceluiasi fenomen (y), in cadrul aceleiasi perioade de timp. Ei pot fi considerati si ca marimi relative de coordonare - cand se compara doua unitati teritoriale, care sunt parti ale aceluiasi ansamblu (tara, continent etc.,) intre ele. In acest caz trebuie existe e o valoare statistica inregistrata in unitatea teritoriala A, notata cu yA si o valoare statistica inregistrata in unitatea teritoriala B, notata cu yB.
Indicii planificarii sunt rezultatul compararii unei valori realizate fata de valoarea aceluiasi fenomen inscrisa intr-un plan (program) sau invers, elaborat la diferite niveluri ale procesului de conducere. Daca se compara nivelul realizat cu nivelul planificat pentru acelasi fenomen din cadrul aceleiasi perioade de timp, atunci se obtine un indice a1 indeplinirii planului. Daca se compara insa nivelul planificat in perioada de plan cu nivelul realizat in perioada de baza pentru acelasi fenomen, atunci se obtine un indice a1 sarcinii de plan. Deci, in acest caz, fata de indicii de dinamica intervine in plus nivelul planificat, notat cu ypl. Ei se folosesc in special, 1a nivel micro.
O alta grupare a indicilor statistici se face dupa nivelul la care s-au inregistrat datele. Dupa cum s-a mai aratat, in practica statistica, la calculul indicilor se foloseste unitati de observare complexe; ca de exemplu: echipa, sectia, intreprinderea, categoria de calificare, lotu1 de produse, parcela etc.
Din acest punct de vedere indicii pot fi:
indici individuali;
indici de grup;
indici generali.
Indicii individuali ai unei variabile statistice (y) sa calculeaza la nivelul unei unitati de observare si se noteaza cu iy1/0 indicele individual arata de cate ori s-a modificat fenomenul y in perioada curenta fata de perioada de baza. De obicei, indicii (individuali si de grup) se exprima sub forma de coeficienti sau procente, adica:
![]() sau
sau ![]()
Indicii individuali se calculeaza ca indici simpli folosind datele inregistrate pentru fiecare variabila la nivelul unitatii de observare folosita:
Pentru fenomenul complex y:

unde:
y - fenomenul complex, de tipul ![]()
x - factorul de tip calitativ (intensiv)
f - factorul de tip cantitativ (extensiv)
Pentru factorul calitativ x:

Pentru factorul cantitativ f

Cei trei indici verifica intotdeauna relatia de sistem:

Relatii de trecere de la indici de dinamica la ritmuri:
![]()
![]()
![]()
unde:
![]() - ritmul de
dinamica pentru fenomenul complex y
- ritmul de
dinamica pentru fenomenul complex y
![]() - ritmul de
dinamica pentru factorul calitativ x
- ritmul de
dinamica pentru factorul calitativ x
![]() - ritmul de
dinamica pentru factorul calitativ f
- ritmul de
dinamica pentru factorul calitativ f
Pe baza indicilor se pot calcula si modificarile absolute ca diferenta intre numaratorul si numitorul indicelui:
![]() ;
; ![]() ;
; ![]()
Indicii de grup ai unei variabile
statistice y se noteaza cu ![]() si se
calculeaza la nivelul unei grupe sau pe intreaga colectivitate, sintetizand variatia medie a fenomenului
studiat. Deci, indicele de grup nu este o suma a indicilor individuali ci
o medie a acestora, exprimand tendinta medie de modificare in timp si
spatiu a caracteristicii la care se refera.
si se
calculeaza la nivelul unei grupe sau pe intreaga colectivitate, sintetizand variatia medie a fenomenului
studiat. Deci, indicele de grup nu este o suma a indicilor individuali ci
o medie a acestora, exprimand tendinta medie de modificare in timp si
spatiu a caracteristicii la care se refera.
In general, elaborarea indicilor de grup ridica cele mai multe probleme. In principal aceste probleme se refera la:
posibilitatea de insumare a elementelor componente;
alegerea bazei de raportare;
alegerea formulei de calcul in functie de natura datelor de care dispunem;
alegerea sistemului de ponderare in functie de continutul indicatorului de comparat si a relatiilor din interiorul sistemului utilizat, astfel incat variatia fenomenului complex sa poata fi descompusa in produsul factorilor care o determina.
Enumerarea acestor probleme arata ca ele trebuie sa se rezolve de la caz la caz pe baza analizei calitative care este obligatorie de fiecare data cand se aplica metoda statistica de studiere a fenomenelor de tip colectiv.
Rezulta de aici ca in teoria si practica statistica se folosesc mai multe tipuri de indici de grup, care se pot si ei clasifica dupa diferite criterii.
Dupa modul de calcul, indicii de grup se pot calcula ca indici agregati, ca indici sub forma de medie (aritmetica sau armonica a indicilor individuali respectivi) sau sub forma de raport a doua medii.
Indicii sub forma de agregat se calculeaza raportand suma nivelurilor partiale ale unui fenomen din perioada curenta la suma nivelurilor partiale corespunzatoare din perioada de baza. Ei se intalnesc ca indice de grup si ca indice general
De exemplu, daca se calculeaza un indice de grup sub forma de agregat pentru fenomenul y, atunci formula de calcul este:
In practica statistica se pot intalni indici agregati ale caror elemente sunt insumabile direct, de exemplu indicele valorii productiei si indicele agregat al unor fenomene neinsumabile direct, pentru care trebuie gasit un element de echivalenta, care in teoria statistica se mai numeste si pondere, cum ar fi indicele volumului fizic al productiei. In acest caz se transforma cantitatile vandute in valori si apoi se insumeaza pentru toate produsele. Pentru a nu influenta valoarea indicelui se folosesc aceleasi preturi si la numaratorul si numitorul indicelui, adica pentru indicele volumului fizic (indicele factorului cantitativ) pot fi considerate ca ponderi preturile din perioada de baza.

Indicele preturilor (indicele factorului calitativ) se construieste utilizand ca ponderi cantitatile din perioada curenta:

![]()
Indicii sub forma de raport a doua medii se intalnesc frecvent in teoria si practica statistica pentru masurarea variatiei unor caracteristici derivate ce se formeaza ca marime medie la nivelul unei grupe sau pe intreaga colectivitate.
In forma generala indicele sub forma de raport a doua medii se prezinta astfel:
![]()
Intr-o forma explicita acest indice se poate scrie astfel incat sa apara distinct ca valoarea unei medii depinde de valorile individuale a1e caracteristicii (x) si de frecventele de aparitie a1e acestora (f) adica:


In functie de structura la care se calculeaza variatia unei caracteristici, indicii sub forma de raport a doua medii pot fi:
indice cu structura variabila;
indice cu structura fixa;
indice al variatiei structurii denumit si indicele modificarilor structurale.
Indicele cu structura variabila se foloseste cand se compara doua valori medii ale caracteristicii variabile in timp sau spatiu in functie de modificarile valorilor individuale (factor calitativ) si de cele ale frecventelor lor de aparitie (factorul cantitativ).
Indicele cu structura fixa se foloseste atunci cand se pune problema sa se masoare numai influenta variatiei valorilor individuale din care s-au calculat mediile in cele doua perioade, anihilandu-se influenta modificarilor din structura colectivitatii.
Din punct de vedere matematic, la calculul indicelui cu structura fixa se pot folosi atat ponderile din perioada de baza, cat si ponderile din perioada curenta, alegerea unei variante sau a celeilalte facandu-se in functie de scopul cercetarii.
Indicele cu structura fixa, folosind ponderile perioadei de baza, corespunde ipotezei ca frecventele perioadei curente sa fie egale cu cele din perioada de baza (f1=f0). In acest caz formula de calcul va fi:


Utilizand frecvente relative (f*) obtinem:

Indicele cu structura fixa, fo1osind ponderile perioadei curente, corespunde ipotezei ca variatia caracteristicii (x) sa se studieze in functie de forma de distributie a frecventelor din perioada curenta, adica f0=f1. Formula de calcul a indicelui cu structura fixa va fi:

 sau
sau
Particularizarea unei formule sau a celeilalte se face de la caz la caz, in raport cu sistemul de ponderare adoptat si cu perioada la care se refera datele.
In cazul ponderarii cu factorul cantitativ din perioada de baza se obtine:


Daca se efectueaza simplificarea corespunzatoare obtinem

Dupa baza de raportare indicii dinamicii fenomenelor pot fi indici cu baza fixa si indici cu baza variabila.
Indicii cu baza fixa sunt aceia in care variatia unei caracteristici se masoara fata de o singura baza de referinta.
Indicii cu baza variabila sunt cei in care variatia caracteristicii se masoara succesiv fata de perioada precedenta sau, in cadrul aceleiasi perioade, fata de o alta unitate teritoriala.
Indicii cu baza fixa si cu baza variabila se calculeaza atat ca indici individuali cat si ca indici de grup.
De exemplu, daca se analizeaza variatia fenomenului complex y pentru o perioada de n+1 ani, indicii de grup de forma agregata se pot calcula cu baza fixa si cu baza variabila:
![]()
 ;
; ![]()
 ; . ;
; . ; ![]()
 ; . ;
; . ; ![]()

respectiv:
![]()
 ;
; ![]()
 ; . ;
; . ; ![]()
 ; . ;
; . ; ![]()

Problemele deosebite apar pentru indicii de grup cu baza fixa sau variabila a unei caracteristici neinsumabile direct in legatura cu alegerea ponderilor.
Dupa ponderile folosite intr-o serie de indici se pot intalni:
indici cu ponderi constante;
indici cu ponderi variabile.
Indicii cu ponderi constante sunt indicii in care pentru toata seria se folosesc aceleasi ponderi.
De exemplu, daca se analizeaza variatia caracteristicii x pentru o perioada de n+1 ani, indicii de grup de forma agregata se pot calcula cu baza fixa si cu baza variabila, in care ponderile folosite notate cu f, sa fie aceleasi pentru toata seria de indici. Pentru aceasta este necesar sa se dispuna de marimile absolute ale caracteristicii x si de ponderile (f) ale acestora pe baza carora se vor elabora seriile dinamice initiale.
Combinand aceste elemente, se vor putea calcula mai multe serii de indici care vor diferi prin baza de raportare si ponderile utilizate. Alegerea ponderilor pentru o serie de indici se face in functie de continutul indicatorului a carui variatie se studiaza. In unele cazuri ponderile sunt alese din perioada de baza a indicelui (de exemplu, la indicele volumului fizic), in alte cazuri ponderile sunt alese din perioada curenta (de exemplu, la indicele preturilor).
In cazul folosirii ponderilor constante luate din perioada de baza a intregii serii (f0) se obtin urmatorii indici cu baza fixa si cu ponderile constante:
![]()
 ;
; ![]()
 ; . ;
; . ; ![]()
 ; . ;
; . ; ![]()

unde: t=0,1,2,3,., n
In mod corespunzator se obtin si indicii cu baza in lant si cu ponderile constante luate din perioada de baza a seriei:
![]()
 ;
;![]()
 ; . ;
; . ;![]()
 ; . ;
; . ;![]()

La calculul acelorasi indici se pot folosi ponderi constante din perioada curenta a seriei (pentru exemplu luat ponderea constanta din perioada curenta a serie este fn).
Indici cu baza fixa si cu ponderea constanta din perioada curenta a indicilor vor fi:
![]()
 ;
; ![]()
 ; . ;
; . ; ![]()
 ; . ;
; . ; ![]()

Indici cu baza in lant si cu ponderile constante din perioada curenta a seriei
![]()
 ;
;![]()
 ; . ;
; . ;![]()
 ; . ;
; . ;![]()

In practica statistica problemele cele mai dificile apar in legatura cu alegerea si folosirea ponderilor la elaborarea indicilor de grup.
Indicii individuali se calculeaza ca indici simpli folosind datele inregistrate pentru fiecare variabila la nivelul unitatii de observare folosita.
Indicii de grup calculati la nivelul intregului ansamblu se calculeaza ca indici agregati. Pentru prezentarea diferitelor sisteme de ponderare se presupune ca variabila y este insumabila direct si ca se descompune integral la nivelul fiecarei unitati in produsul dintre variabila x - cu caracter de marime derivata - si variabila f cu caracter de variabila cantitativa neinsumabila direct. Aceasta inseamna ca pentru indicii de grup ai celor doua variabile-factori se va folosi tot un indice agregat in care succesiv fenomenul de indexat este variabil, iar celalalt are caracter de pondere.
Un prim sistem de ponderare este cel propus in 1864 de catre statisticianul belgian Laspeyres, la care ponderile folosite sunt cele din perioada de baza. In acest caz se obtine:
indicele variabilei calitative x de tip Laspeyres, este:
![]()

indicele variabilei cantitative f de tip Laspeyres, este:
![]()

Din considerente practice, insa, se intalnesc frecvent cazuri cand si pentru variabila calitativa se foloseste sistemul de ponderare Laspeyres, mai ales in cazul cand lipsesc sau de obtin cu intarziere datele pentru ponderile curente. Teoretic este de admis, ca aceasta substituire se poate face cand exista o stabilitate a structurii ponderilor.
Un alt sistem de ponderare este cel propus in 1874 de catre statisticianul german Paasche, la care ponderile utilizate sunt cele din perioada curenta a indicelui.
pentru indicele factorului cantitativ, formula va fi:
![]()

pentru indicele factorului calitativ, formula va fi:
![]()

In teoria indicilor statistici se mai intalnesc si alte sisteme de ponderare. care tin seama de ponderile din ambele perioade de calcul.
Indicele preturilor calculat de Edgeworth se bazeaza pe cumularea cantitatilor din perioada de baza cu cele din perioada curenta, pe care le foloseste drept ponderi pentru variatia preturilor. Pretul fiind o variabila calitativa, formula poate fi generalizata astfel:
![]()

Avand calculata intreaga contributie a fiecarui factor, se poate calcula gradul de determinatie al factorilor la sporul total al variabilei (y). Aceasta se realizeaza pornind de la relatia de sistem:
![]()
si se obtine in expresie relativa a fiecarui factor:
-
factor calitativ: ![]()
![]()
- factor cantitativ: ![]()
In cazul procedeului determinarii influentei separate a factorilor coeficientul determinatie totala este egal cu coeficientul ponderii determinat anterior. In cazul in care ponderea factorului calitativ (x) depaseste 50%, admitem ca fenomenul y se modifica pe cale intensiva; in caz contrar are loc o modificare extensiva.
Sistemul de indici ai valorii, volumului fizic si ai preturilor, calculati ca indici agregati .
Daca se noteaza cantitatea de marfuri cu q, pretul unitar cu p iar valoarea cu v, rezulta urmatoarele relatii:
- pentru perioada de baza v0 = qo . p0
- pentru perioada curenta v1= q1 . p1
Indicele individual al valorii se calculeaza raportand valoarea din perioada curenta la valoarea din perioada de baza folosind formula:

Indicele de grup al valorii dupa formula:

Modificarea absoluta (D) a valorii se determina dupa formula:
Dv = Sq1pl - Sq0p0
Indicele individual al volumului fizic arata de cate ori s-a modificat sub aspect cantitativ productia in perioada curenta in raport cu cea din perioada de baza.
Formula de calcul este:

Indicele de grup al volumului fizic se calculeaza fie un indice de tip Laspeyres fie un indice de tip Paasche.
Indicele volumului fizic calculat cu preturile din perioada de baza:

Indicele volumului fizic calculat cu preturile din perioada curenta:

Modificarea absoluta a volumul fizic al productiei sau circulatiei de marfuri se noteaza cu Dq arata cu cat ar fi crescut (scazut) in marimi absolute valoarea productiei in perioada curenta fata de cea din perioada de baza, daca preturile ar fi ramas aceleasi. Deci formula de calcul este:
Dv(q)(L)1/0 Sq1p0 - Sq0p0
In practica statistica, pentru determinarea indicelui volumului fizic se folosesc si preturile comparabile in acest caz indicele se va calcula dupa formula:

in care:
p = pret comparabil.
Indicele individual al pretului (ip1/0 ) se calculeaza raportand pretul din perioada curenta la pretul din perioada de baza:
![]()
Indicele preturilor se calculeaza ca indice de grup, tinand seama ca pretul este un atribut al produselor respective. Deci, pe ansamblu trebuie avute in vedere si utilitatile la care se refera structura colectivitatii productiei vandute. Elementul pondere este aici cantitatea din fiecare produs.
Si aici apar doua variante:
- indicele preturilor de tip Laspeyres:

- indicele preturilor de tip Paasche:

Economia (risipa) realizata pe seama modificarii preturilor Dp se calculeaza dupa formula:
Dv(p)(P) Sp1q1 - Sp0ql
Analizand cei trei indici de grup, rezulta ca in practica statisticii din tara noastra, indicele volumului fizic se calculeaza dupa formula propusa de Laspeyres, iar indicele preturilor, de regula dupa formula propusa de Paasche. Pe langa argumentele legate de continutul fenomenului de indexat si care au fost prezentate la interpretarea comparativa a celor doi indici, se mai adauga si unele aspecte legate de valoarea ponderilor utilizate.
Folosirea diferentiata a celor doua sisteme de ponderare satisface in plus si relatia de descompunere a indicelui valorii in produsul indicilor factoriali, care se verifica in toate cazurile pentru indicii individuali.
Deci, intre cei trei indici exista urmatoarea relatie: indicele valorii este egal cu indicele volumului fizic inmultit cu indicele preturilor:
Iv = Iv(q)(L)1/0
.I v(p)(P)1/0 de
unde  , iar
, iar 
Daca se inlocuiesc cei trei indici cu formulele lor de calcul se obtine:

Daca cei doi indici factoriali vor fi calculati cu acelasi sistem de ponderare, atunci modificarea valorii nu se mai descompune integral pe cei doi factori de influenta si apare un rest nedescompus, care in literatura de specialitate se apreciaza ca este rezultatul interactiunii dintre factori.
Aceasta relatie se foloseste frecvent in practica statistica atunci cand nu se pot calcula direct cei trei indici. Este suficient sa se cunoasca doi dintre cei trei indici pentru a calcula pe cel de al treilea.
Relatia de produs a indicilor factoriali se transforma in relatie de insumare a modificarilor absolute stabilite pe seama factorilor inregistrati.
Modificarea absoluta a valorii productiei sau circulatiei de marfuri este egala cu suma modificarilor absolute calculate in functie de modificarea volumului fizic si a preturilor:
Dv Dv(q) Dv(p)
Si in acest caz este suficient sa se cunoasca doua modificari absolute pentru a determina pe cea de a treia din cadrul sistemului de indici care a stat la baza calcularii lor.
Modificarea absoluta a volumului fizic este egala cu modificarea absoluta a valorii, minus modificarea absoluta a preturilor:
Dv(q) Dv Dv(p)
Modificarea absoluta a preturilor este egala cu modificarea absoluta a valorii productiei, minus modificarea absoluta a volumului fizic al productiei:
Dv(p) Dv Dv(q)
Din considerente practice si mai ales cand se studiaza izolat evolutia preturilor si a tarifelor pentru marfuri si servicii, se pot calcula in acest scop pentru ambii factori cu ponderi Laspeyres fara insa sa se mai puna problema ca ei sa fie incadrati intr-un sistem.
Deci, in acest caz se dispune de urmatoarele relatii derivate din formula indicelui agregat al volumului fizic:
 , in care xi
= iq1/0;
f = q0p0; xf = q1p0
, in care xi
= iq1/0;
f = q0p0; xf = q1p0
Este evident faptul ca, pentru acest caz, este avantajos sa se foloseasca indicele aritmetic ponderat al volumului fizic, deoarece se cunoaste valoarea din perioada de baza care constituie ponderea pentru aceasta forma de medie:
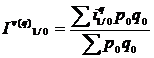
Daca in formula de mai sus se inlocuieste indicele individual cu formula sa de calcul, se demonstreaza ca se ajunge la acelasi rezultat ca si in cazul cand s-ar folosi un indice agregat:
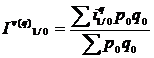


Indicele aritmetic al volumului fizic se calculeaza ca o medie aritmetica a indicilor individuali ai acestuia, ponderati cu valoarea din perioada de baza. El se foloseste cand nu se cunosc separat cantitatile si preturile, ci numai valoarea obtinuta.
Pentru indicele preturilor sub forma de medie se porneste de la aceleasi conditii:
sa fie o medie a indicilor individuali ai preturilor;
sa fie o forma transformata a indicelui agregat al preturilor, deci sa foloseasca ca ponderi numaratorii sau numitorii partiali.
Indicele armonic a1 preturilor se calculeaza ca o medie armonica a indicilor individuali ai preturilor, ponderata cu valoarea marfurilor vandute in perioada curenta, adica:

|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3511
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved