| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
REZOLVAREA
Se considera sistemul supradeterminat de ecuatii algebrice liniare :
![]() (1)
(1)
unde A este o
matrice reala cu m linii si n coloane, m > n, iar b este un vector (coloana)
real, cu m componente. Matricea A se presupune avand coloanele liniar
independente (rang(A) = n ). Problema consta in
determinarea unei pseudosolutii ![]() ,
a sistemului (1), in sensul celor mai mici patrate (CMMP), adica a unui vector
,
a sistemului (1), in sensul celor mai mici patrate (CMMP), adica a unui vector ![]() cu proprietatea:
cu proprietatea:
![]() (2)
(2)
unde ![]() semnifica norma vectoriala euclidiana.
semnifica norma vectoriala euclidiana.
Rezolvarea numerica eficienta a acestei probleme se bazeaza pe triangularizarea ortogonala a matricii sistemului. O modalitate de a realiza aceasta este data de folosirea reflectorilor Householder. Aplicand acestia, la stanga, in ambii membri ai ecuatiei (1), se obtine, in primele n linii, un sistem determinat de ecuatii liniare, cu matrice superior triunghiulara. Acesta din urma este rezolvat prin substitutie inversa, conducand la obtinerea pseudosolutiei in sensul celor mai mici patrate.
APLICATIE:
Sa se realizeze, in mediul de programare MATLAB, programul pentru rezolvarea unui sistem supradeterminat de ecuatii liniare, in sensul CMMP, folosind transformari ortogonale de echivalenta. Programul va compara solutia gasita cu cea furnizata de mediul MATLAB, utilizand o functie similara procedurii studiate.
In realizarea programului se vor parcurge urmatoarele etape, descrise partial in limbajul pseudocod:
1. Introducere parametru de control al procedurii de triangularizare, in variabila EPS.
2. Introducere
dimensiuni matrici sistem, in variabilele m (numar ecuatii) si, respectiv, n
(numar necunoscute). Conditie de indeplinit: ![]() .
.
3. Alocare spatiu de memorie pentru matricea sistemului, in variabila a, prin initializarea acesteia cu o matrice nula, de dimensiuni m x n. Introducerea elementelor matricii sistemului se face pe linii. Reluare introducere in caz de eroare. Salvare matrice a:
ATRIBUIE aa a
4. Triangularizare ortogonala matrice sistem (descompunere QR):
ATRIBUIE u ← zeros(m,n)
ATRIBUIE beta ← zeros(n,1)
_ PENTRU k = 1,n EXECUTA
ATRIBUIE sum ← sqrt( (a(k:m,k))'*a(k:m,k) )
_ DACA ( a(k,k) >= 0 ) ATUNCI
| ATRIBUIE semn ← 1
|ALTFEL
|_ ATRIBUIE semn ← -1
ATRIBUIE sigma ← semn*sum
ATRIBUIE u(k,k) ← a(k,k) + sigma
ATRIBUIE u(k+1:m,k) ← a(k+1:m,k)
ATRIBUIE beta(k) ← sigma*u(k,k)
_ DACA ( abs(beta(k)) < EPS ) ATUNCI
|_ SCRIE 'algoritmul va esua: beta < EPS'
ATRIBUIE a(k,k) ← - sigma
ATRIBUIE a(k+1:m,k) ← zeros(m-k,1)
_ PENTRU j = k+1,n EXECUTA
| ATRIBUIE sum ← u(k:m,k)'*a(k:m,j)
| ATRIBUIE tau ← sum/beta(k)
|_ ATRIBUIE a(k:m,j) ← a(k:m,j) - tau*u(k:m,k)
SCRIE 'k = ',k
SCRIE 'a = ',a
ATRIBUIE flag 0
ATRIBUIE i ← 1
_ CAT TIMP ( (i <= n) SI (flag = 0) ) EXECUTA
_ DACA ( abs(a(i,i)) < EPS ) ATUNCI
|_ ATRIBUIE flag ← 1
ATRIBUIE i ← i+1
_ DACA ( flag = 1 ) ATUNCI
SCRIE 'matrice deficienta de rang'
ATRIBUIE rang ← rank(a)
SCRIE 'rang(a) =', rang
5. Alocare spatiu de memorie pentru termenul liber al sistemului, in variabila b, prin initializarea acesteia cu un vector coloana nul, cu m componente. Introducerea elementelor termenului liber al sistemului se face pe linii. Reluare in caz de eroare. Salvare vector b:
ATRIBUIE bb b
6. Transformare ortogonala termen liber sistem :
_ PENTRU k = 1,n EXECUTA
ATRIBUIE sum ← u(k:m,k)'*b(k:m)
ATRIBUIE taub ← sum/beta(k)
ATRIBUIE b(k:m) ← b(k:m) - taub*u(k:m,k)
SCRIE 'b =', b
7. Calcul solutie sistem prin substitutie inapoi :
ATRIBUIE x ← zeros(n,1)
ATRIBUIE x(n) ← b(n)/a(n,n)
_ PENTRU i = n-1,(pas = -1),1 EXECUTA
ATRIBUIE sum <-- a(i,i+1:n)*x(i+1:n)
ATRIBUIE x(i) <-- (b(i) - sum)/a(i,i)
8. Calcul reziduu asociat solutiei x:
ATRIBUIE b(1:n) <-- zeros(n,1)
_ PENTRU k = n,(pas = -1),1 EXECUTA
ATRIBUIE sum ← (u(k:m,k))'*b(k:m)
ATRIBUIE taud ← sum/beta(k)
ATRIBUIE b(k:m) ← b(k:m) - taud*u(k:m,k)
ATRIBUIE nr norm(b,2)
9. Calcul solutie si reziduu asociat, folosind functia MATLAB :
ATRIBUIE x_bs ← aabb
ATRIBUIE r_bs ← bb - aa*x_bs
ATRIBUIE nr_bs ← norm(r_bs,2)
10. Afisare rezultate: x, b (reziduu asociat lui x), nr, x_bs, r_bs, nr_bs
OBSERVATIE :
1. Descrierea anterioara a programului de realizat foloseste urmatoarele functii MATLAB: zeros, sqrt, abs, rank, , norm.
Programul se va rula pentru urmatoarele date de intrare:
EPS = 1.e-16
I.)
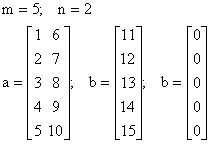
II.)

|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2647
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved