SERII DE REPARTITIE

SERII DE REPARTITIE

1. Seria de repartitie

Gruparea unitatilor statistice ale unei colectivitati in functie de caracteristici atributive calitative sau cantitative are ca efect obtinerea seriilor de repartitie (distributie). Specific seriilor de repartitie este faptul ca indiferent de tipul lor, spatiul si timpul sunt constante.

Numarul de unitati statistice corespunzatoare fiecarei grupe se numesc frecvente absoluta, se noteaza cu f_i, iar suma acestora este egala cu numarul de unitati statistice ale colectivitatii (N).

(4.1)

Seriile de repartitie pot fi clasificate dupa mai multe criterii:

a)         Daca luam in calcul modul de variatie a caracteristicii de grupare se disting doua tipuri de serii de distributie:

Serie de repartitie dupa variante ale caracteristicii de grupare, construite de regula in cazul in care caracteristica atributiva de grupare este cu variatie discreta, iar numarul variantelor este relativ mic, sau in cazul in care caracteristica de grupare este calitativa;

Perechile (x_i, f_i) reprezinta termenii seriei de repartitie. Daca f₁=f₂==f_k atunci de regula nu se mai scrie sirul frecventelor, iar sirul variantelor caracteristicii x , x₂, , x_k poarta numele de repartitie simpla.

De cele mai multe ori insa frecventele difera intre ele si prin urmare seria poarta numele de repartitie de frecvente.

Serie de repartitie dupa intervale de variatie, construite de regula in cazul in care caracteristica de grupare este cu variatie continua.

In urma unei astfel de grupari, pe intervale egale, se obtine deci seria de repartitie pe intervale de variatie care se prezinta sub forma:

Limita inferioara inclusa in interval

Indicarea limitelor intervalelor de variatie se poate face in doua moduri:

limita superioara a intervalului se preia ca limita inferiara a intervalului urmator, adica:

x_i^sup= x_i+1^inf

cele doua limite sunt distincte fiind distantate cu o unitate egala cu cifra de cel mai mic ordin.

Primul caz, cand se considera ca limita superioara este inclusa in interval este utilizata daca caracteristica de grupare are o variatie continua, iar cel de-al doilea caz corespunde variatiei discrete.

In primul caz, in calcule intervalul este reprezentat de centrul acestuia care se obtine dupa relatia:

In al doilea caz centrul intervalului se determina conform cu relatia:

Unde h_i este lungimea intervalului.

Pentru determinarea intervalului de variatie se poate, apela in cazul in care nu se cunoaste numarul de grupe, la formula lui H.A. Sturges:

(4.2)

in care:

x_max, x_min - varianta maxima si varianta minima a caracteristicii de grupare;

N - numarul total al unitatilor statistice ale colectivitatii.

b)         Daca avem in vedere numarul variabilelor (caracteristicilor) de grupare, seriile de repartitie pot fi:

serii de repartitie unidimensionale care se construiesc dupa o singura variabila de grupare (vezi tabelul 4.1 sau 4.2);

serii de repartitie bidimensionale care se construiesc dupa doua variabile de grupare, de regula interdependente, din care una este principala, iar cealalta secundara (vezi tabelul 4.3).

Seria de repartitie bidimensionala se prezinta sub forma unui tabel cu dubla intrare, in care pe linii se inscriu variantele caracteristicii principale X x₁, x_2, x_k), iar pe coloane cele ale caracteristicii secundare Y y₁, y_2, y_p), iar in interiorul tabelului frecventele f_ij , respectiv numarul de unitati statistice purtatoare atat a variantei x_i a caracteristicii X, cat si a variantei y_j a caracteristicii Y.

Pentru caracteristicile X si Y, suma frecventelor absolute f_ij este egala cu marimea colectivitatii:

(4.3)

Se noteaza cu punct totalul dupa indicele i sau dupa indicele j, astfel:

- totalul frecventelor absolute f_ij insumate dupa j

- totalul frecventelor absolute f_ij insumate dupa i

- totalul frecventelor absolute f_ij insumate si dupa i si dupa j

, (4.4)

Pentru prezentarea seriilor de repartitie se pot utiliza si alti indicatori de frecventa obtinuti pe baza frecventelor absolute.

Daca frecventele absolute f_j se impart la numarul total al colectivitatii, se obtin frecvente relative notate cu f_i^*.

Frecventele relative se pot exprima si in procente. Suma frecventelor relative este egala cu 1 sau 100% daca sunt exprimate in procente.

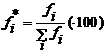cu (4.5)

Pe baza frecventelor absolute, (sau a frecventelor relative) se pot determina frecventele cumulate, notate cu F_i (respectiv F_i^*).

Cumularea frecventelor se poate face succesiv pornind fie din capatul de sus al seriei, fie din capatul de jos, obtinand astfel pentru fiecare valoare a seriei frecvente cumulate crescator sau descrescator.

Reprezentari grafice ale seriei de repartitie

Reprezentarile grafice ale seriilor de repartitie urmaresc sa puna in evidenta anumite aspecte ale structurii colectivitatilor studiate sau ale formei distributiei, aspecte care se observa mai greu pe baza seriei tabelate.

Exista mai multe tipuri de grafice utilizate in reprezentarea seriilor de repartitie unidimensionale, dar cele mai intalnite raman diagramele prin coloane, histograma, poligonul frecventelor si curba frecventelor cumulate (ogiva).

Diagrama prin coloane este poate cea mai simpla si cea mai raspandita reprezentare grafica. Indicatorii sunt reprezentati prin benzi a caror lungime este proportionala cu nivelul acestora, iar latimea este aceeasi pentru toate benzile diagramei.

In practica sunt utile mai ales pentru reprezentarea seriilor de repartitie cu caracteristica de grupare calitativa.

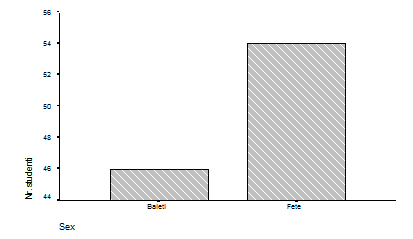
Fig. 4.1. Diagrama prin coloane

Histograma este o forma particulara a diagramei prin coloane fiind specifica seriei de repartitie cu caracteristica numerica. Pe ordonata in dreptul diviziunilor scarii de reprezentare se trec frecventele distributiei.

Daca avem de-a face cu o distributie pe variante ale caracteristicii de grupare, din dreptul diviziunilor de pe abscisa se ridica perpendiculare a caror inaltime este proportionala cu nivelul frecventelor corespunzatoare, obtinandu-se astfel histograma prin batoane.

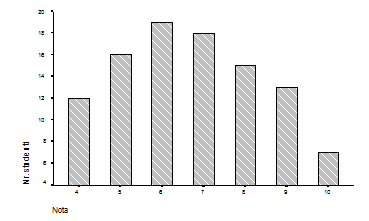
Fig. 4.2. Histograma prin batoane

Daca distributia este pe intervale de variatie ale caracteristicii de grupare, de pe abscisa, din dreptul intervalelor dintre diviziuni se ridica dreptunghiuri a caror inaltime este proportionala cu frecventele corespunzatoare, obtinandu-se histograma prin dreptunghiuri.

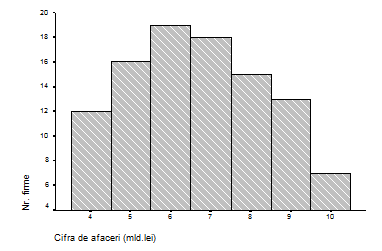
Fig.4.3. Histograma prin dreptunghiuri

Poligonul frecventelor este un alt tip de grafic utilizat pentru reprezentarea grafica a seriilor de repartitie cu caracteristica numerica. Se poate construi pe baza histogramei corespunzatoare unind varfurile batoanelor, sau centrele bazelor superioare ale dreptunghiurilor, sau se poate construi direct pe baza seriei ridicand de pe axa absciselor perpendiculare ale caror inaltimi sunt proportionale cu frecventele respective si apoi unind prin segmente de dreapta capetele acestor perpendiculare.

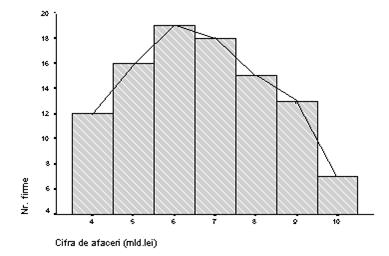
Fig.4.4. Histograma prin dreptunghiuri si Poligonul frecventelor

Curba frecventelor cumulate sau ogiva reprezinta una dintre cele mai clare si mai utile reprezentari grafice ale seriilor de repartitie. Pentru construirea ogivei pe ordonata, in dreptul diviziunilor se trec frecventele cumulate.

Pentru distributiile pe intervale de variatie, de pe abscisa, din dreptul intervalelor se ridica dreptunghiuri cumulative a caror inaltime este proportionala cu nivelul frecventelor cumulate corespunzator. Unind extremitatile din dreapta ale bazelor superioare ale acestor dreptunghiuri se obtine ogiva.

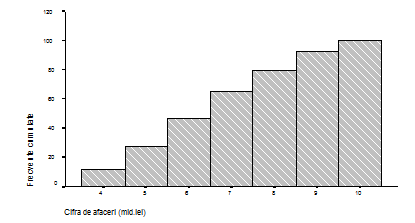
Fig.4.5. Histograma prin dreptunghiuri cumulative

Fig. 4.6. Ogiva - Curba frecventelor cumulate

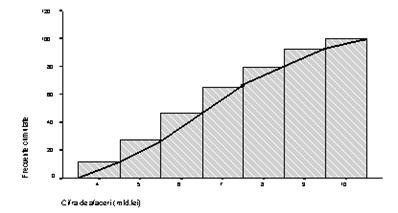
Daca distributia este pe variante ale caracteristicii de grupare, din dreptul diviziunilor de pe abscisa se ridica batoane cumulative, ogiva obtinandu-se prin unirea varfurilor acestor batoane.