| CATEGORII DOCUMENTE |
| Demografie | Ecologie mediu | Geologie | Hidrologie | Meteorologie |
ANALIZA LEGATURILOR DINTRE VARIABILELE UNEI REPARTITII MULTIDIMENSIONALE
Obiective
Concepte de baza
Rezultate asteptate
Dupa parcurgerea acestui modul se cere studentului sa stapaneasca notiunile de corelatie si regresie, sa poata identifica existenta unei eventuale legaturi intre doua marimi. De asemenea sa stie masura intensitatea legaturii dintre variabile, fie ele cantitative sau calitative. Se urmareste si cunoasterea metodelor de modelare functionala a legaturilor.
Sinteza
Ne propunem abordarea unor metode statistice caracteristice studiului seriilor multidimensionale. Scopul acestora este de a identifica si utiliza eventualele legaturi care se pot manifesta intre doua sau mai multe variabile. Prezinta interes: existenta legaturii, intensitatea acesteia, forma functionala a legaturii, parametrii si reprezentativitatea ei privind fenomenul cercetat. Problematica legaturilor dintre variabile este foarte curent intalnita in economie. Spunem ca salariul unui angajat este in functie de productivitatea muncii sale, vechimea in munca, responsabilitatea activitatii sale, etc ; sau cererea dintr-un produs este in functie de pretul produsului, venitul consumatorilor, etc. De fiecare data, atat in teoria economica, cat si in aplicatii se intalneste expresia "fie functia cererii.". In realitatea economica insa, aceasta functie nu se da, nu se cunoaste, ci trebuie estimata pornind de la o baza de date. Aceasta problema de estimare a unei functii si alte probleme colaterale ei fac obiectul acestui capitol.
Pentru a putea aborda studiul legaturilor dintre variabile trebuie sa stim in primul rand daca exista sau nu o legatura intre variabilele studiate (sau intre fenomenele pe care acestea le reprezinta) si care este natura acestora. Putem clasifica legaturile dinte variabile astfel :
1. Legatura
nula. Semnifica lipsa oricarei legaturi intre doua sau mai multe fenomene
sau variabile care cuantifica fenomenele. De exemplu, o
legatura nula se manifesta intre inaltimea unui angajat si salariul acestuia
sau intre produsul intern brut al unei tari si varsta primului ministru.
Din punct de vedere statistic, spunem ca intre doua variabile X si Y
exista o legatura nula, sau nu exista legatura, daca ![]() .
.
2. Legatura
determinista. Spunem ca intre variabilele X si Y exista o
legatura determinista daca unei valori a lui X ii corespunde o singura
valoare a lui Y. Astfel de legaturi se intalnesc in special in fizica,
unde de exemplu viteza este egala cu distanta impartita la timp: ![]() , sau forta
este egala cu masa inmultita cu acceleratia:
, sau forta
este egala cu masa inmultita cu acceleratia: ![]() . Astfel de exemple exista si in economie,
unde rata profitului este egala cu profitul impartit la cifra de afaceri:
. Astfel de exemple exista si in economie,
unde rata profitului este egala cu profitul impartit la cifra de afaceri: ![]() .
Legatura este determinista pentru ca variabila
.
Legatura este determinista pentru ca variabila ![]() este perfect determinata de celelalte doua:
este perfect determinata de celelalte doua: ![]() si
si ![]() Adica pentru o anumita valoare a profitului si
o anumita valoare a cifrei de afaceri nu putem avea decat o singura valoare a
ratei profitului.
Adica pentru o anumita valoare a profitului si
o anumita valoare a cifrei de afaceri nu putem avea decat o singura valoare a
ratei profitului.
Legatura statistica. Se mai numeste si
stocastica sau probabilista. Este tipul de legatura cel mai des intalnita in
stiintele sociale, deci si in economie. Fiecarei valori ![]() a variabilei X ii corespunde o
distributie de valori ale variabilei Y. Matematic, o astfel de legatura
se exprima sub forma
a variabilei X ii corespunde o
distributie de valori ale variabilei Y. Matematic, o astfel de legatura
se exprima sub forma ![]() , unde am
notat prin
, unde am
notat prin ![]() componenta aleatoare reziduala, datorata
actiunii asupra lui Y a celorlalti factori decat X. Desi s-ar
putea spune ca prin luarea in considerare a tuturor factorilor care
influenteaza variabila Y, legatura este intrinsec determinista, in
stiintele economice vom intalni aproape intotdeauna un numar foarte mare de
factori, care nu pot fi identificati si cuantificati in totalitatea lor. Asfel,
functia care il expliciteaza pe Y are doua componente: una determnista,
componenta aleatoare reziduala, datorata
actiunii asupra lui Y a celorlalti factori decat X. Desi s-ar
putea spune ca prin luarea in considerare a tuturor factorilor care
influenteaza variabila Y, legatura este intrinsec determinista, in
stiintele economice vom intalni aproape intotdeauna un numar foarte mare de
factori, care nu pot fi identificati si cuantificati in totalitatea lor. Asfel,
functia care il expliciteaza pe Y are doua componente: una determnista, ![]() ,
cuprinzand variabilele cuantificabile de care depinde Y, si una
aleatoare,
,
cuprinzand variabilele cuantificabile de care depinde Y, si una
aleatoare, ![]() ,
cuprinzand variabilele ce nu au putut fi cuantificate.
,
cuprinzand variabilele ce nu au putut fi cuantificate.
Sudiul legaturilor dintre variabile s-a dezvoltat intr-o disciplina aparte, numita econometrie. In capitolul de fata nu ne propunem deci decat o introducere in aceasta problematica, fara a aborda elemente de inferenta statistica specifice acestor legaturi. In cele ce urmeaza vom prezenta cateva aspecte legate de variabile si fenomenele reprezentate de acestea, probleme atat de natura aparatului statistic utilizat, cat si de aplicabilitatea lui in contextul economic.
Analiza legaturii dintre variabilele unei repartitii multidimensionale presupune abordarea urmatoarelor probleme, care se pot constitui si in etape ce trebuie parcurse in demersul statistic necesar:
Organizarea rezultatelor observarii populatiei sau esantionului in raport cu variabilele cercetate
Analiza statistica a existentei legaturii
Analiza statistica a intensitatii legaturii sau a gradului de asociere dintre variabilele observate
Formularea unor ipoteze cu privire la forma matematica a legaturii
Estimarea parametrilor functiei de regresie
Analiza reprezentativitatii functiei de regresie
Aceste etape pot fi parcurse integral sau partial, in functie de natura variabilelor. Pentru variabilele calitative nu vor fi parcurse (in statistica descriptiva) decat primele trei, deoarece posibilitatile de prelucrare sunt mai reduse. In schimb, toate cele sase etape pot fi parcurse in cazul variabilelor cantitative.
1. Organizarea rezultatelor observarii populatiei sau esantionului in raport cu variabilele cercetate
In scopul utilizarii facile a informatiei culese la nivelul populatiei sau esantionului, rezultatele observarii vor fi sistematizate intr-o forma convenabila prelucrarii lor. Se prefera de obicei o forma tabelara a prezentarii, care poate sugera unele idei de lucru pentru etapele urmatoare, prin unele remarci cu privire la valorile pe care le-au inregistrat variabilele.
2. Analiza statistica a existentei legaturii
In studiul analizei existentei legaturii vom folosi atat elemente de statistica deja abordate in capitolele anterioare, cum ar fi tabelele si graficele, cat si parametri (coeficienti specifici acestui capitol. Deoarece prezinta particularitati distincte, vom aborda separat problematica subcapitolului in functie de tipul variabilelor.
2.1. Analiza statistica a existentei legaturii pentru variabile calitative
Un prim instrument ce ne sta la indemana este tabelul de corelatie, un tabel cu doua intrari, reprezentand o repartitie bidimensionala. Modul de constructie al unui astfel de tabel se cunoaste de la seriile statistice.
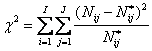
Ca o concluzie, distingem cele doua cazuri:
Daca ![]() nu exista legatura intre variabile
nu exista legatura intre variabile
2) Daca ![]() exista legatura intre variabile
exista legatura intre variabile
Procedeul prezentat anterior ne permite identificarea existentei legaturii dintre doua variabile, dar nu si a intensitatii acesteia. Totusi, pornind de la el se pot construi coeficienti care sa ne permita si aprecierea intensitatii legaturii, asa cum se va vedea in sectiunile urmatoare.
2.2. Analiza statistica a existentei legaturii pentru variabile cantitative
Asa cum s-a vazut in capitolul anterior, daca dispunem de o repartitie bidimensionala, putem descompune varianta totala a variabilei de explicat Y ca suma a variantelor datorate variabilei explicative X si respectiv celorlalti factori, adica:
![]()
Daca nu exista legatura, adica X nu are nici
o influenta asupra lui Y, mediile conditionate ![]() vor fi identice, iar dispersia lor va fi nula
vor fi identice, iar dispersia lor va fi nula ![]() .
.
Putem retine deci ca regula de decizie in statistica descriptiva:
Daca ![]() nu exista legatura intre variabile
nu exista legatura intre variabile
Daca ![]() exista legatura intre variabile
exista legatura intre variabile
Analiza statistica a intensitatii legaturii sau a gradului de asociere dintre variabilele observate
Ca si in cazul existentei legaturii, o prima apreciere a intensitatii se poate face pe baza tabelului de corelatie si a norului de puncte. Cu cat frecventele mai mari sunt mai grupate in jurul uneia din diagonalele tabelului de exemplu sau punctele norului sunt mai grupate in jurul unei linii, cu atat legatura este mai intensa. In ceea ce priveste metodele cantitative de apreciere, ele sunt mult mai precise si ne pot oferi valori numerice ale intensitatii sau gradului de asociere. Aceste metode sunt insa diferite in functie de tipul variabilelor si de aceea le vom aborda separat.
1. Gradul de asociere sau intensitatea legaturii dintre variabilele calitative
Coeficientul de asociere (contingenta) al lui Pearson
Relatia de calcul a coeficientului este:
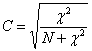
unde N este volumul populatiei.
daca ![]() legatura este nula (lipsa legaturii)
legatura este nula (lipsa legaturii)
daca ![]() legatura este de intensitate slaba
legatura este de intensitate slaba
daca ![]() legatura este de intensitate medie
legatura este de intensitate medie
daca ![]() legatura este de intensitate puternica
legatura este de intensitate puternica
2. Gradul de asociere sau intensitatea legaturii dintre variabilele ordinale
Coeficientul de corelatie a rangurilor al lui
Pentru a putea utiliza acest indicator toate unitatile populatiei trebuie sa poata fi ordonate in raport cu variabilele pentru care cercetam intensitatea legaturii. Presupunem o populatie de volum n observata in raport cu m variabile.
Pentru a putea construi coeficientul, vom
defini mai intai indicatorul de concordanta (P) si respectiv
indicatorul de discordanta (Q). Pe baza indicatorilor de concordanta
si discordanta construim coeficientul de corelatie simpla a rangurilor
al lui
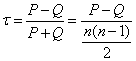
In cazul unei legaturi
directe de intensitate maxima, P va lua valoare sa maxima, iar Q
pe cea minima, adica: ![]() iar
iar ![]() , deci
, deci ![]() .
.
In cazul unei legaturi
inverse de intensitate maxima, P va lua valoare sa minima, iar Q
pe cea maxima, adica: ![]() iar,
iar, ![]() deci
deci ![]() .
.
In cazul lipsei legaturii ![]() , iar
, iar ![]() .
.
Putem determina astfel
intervalul in care va fi cuprins ![]() , respectiv
, respectiv
![]() .
Interpretarea intensitatii legaturii pe baza acestui coeficient se va face astfel:
.
Interpretarea intensitatii legaturii pe baza acestui coeficient se va face astfel:
daca ![]() legatura este directa
legatura este directa
daca ![]() legatura este nula
legatura este nula
daca ![]() legatura este inversa
legatura este inversa
daca ![]() legatura este de intensitate slaba
legatura este de intensitate slaba
daca ![]() legatura este de intensitate medie
legatura este de intensitate medie
daca ![]() legatura este de intensitate puternica
legatura este de intensitate puternica
Coeficientul de corelatie a rangurilor al lui Spearman
Ca si
coeficientul similar propus de ![]() dintre
ranguri pentru aceeasi unitate a populatiei relativ la cele doua variabile.
Coeficientul are urmatoarea expresie:
dintre
ranguri pentru aceeasi unitate a populatiei relativ la cele doua variabile.
Coeficientul are urmatoarea expresie:
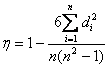
Limitele celor doi coeficienti sunt aceleasi, la fel si interpretarile valorilor numerice.
Intensitatea legaturii dintre variabilele cantitative
Raportul de corelatie
Folosind regula de adunare a variantelor descompunem varianta totala a variabilei de explicat Y ca suma a variantelor datorate variabilei explicative X si respectiv celorlalti factori, adica:
![]()
Varianta explicita ![]() este cu atat mai mare
cu cat mediile conditionate
este cu atat mai mare
cu cat mediile conditionate ![]() sunt mai diferite intre ele. Ceea ce le face
sa difere este numai influenta lui X, deoarece am impartit populatia in
grupe avand ca unic criteriu valorile lui X. Este firesc deci sa folosim
varianta explicita ca o marime absoluta a intensitatii legaturii dintre X
si Y si ponderea variantei explicite in varianta totala ca o marime
relativa. Raportul de corelatie are expresia:
sunt mai diferite intre ele. Ceea ce le face
sa difere este numai influenta lui X, deoarece am impartit populatia in
grupe avand ca unic criteriu valorile lui X. Este firesc deci sa folosim
varianta explicita ca o marime absoluta a intensitatii legaturii dintre X
si Y si ponderea variantei explicite in varianta totala ca o marime
relativa. Raportul de corelatie are expresia:
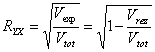
sau sub forma ei matematica:
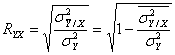
Pentru a-i gasi limitele ne raportam la cele doua situatii extreme:
daca nu exista legatura intre X si Y,
mediile conditionate ![]() sunt egale intre ele, deci
sunt egale intre ele, deci ![]() si
si ![]()
daca legatura este de
intensitate maxima, nu exista influente ale altor factori decat X asupra
lui Y, nu exista variatie in cadrul grupelor, deci ![]() si
si ![]() .
.
In consecinta, raportul de corelatie apartine intervalului ![]() .
Interpretarea intensitatii legaturii pe baza acestui coeficient se va face astfel:
.
Interpretarea intensitatii legaturii pe baza acestui coeficient se va face astfel:
daca ![]() legatura este nula
legatura este nula
daca ![]() legatura este de intensitate slaba
legatura este de intensitate slaba
daca 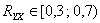 legatura este de intensitate medie
legatura este de intensitate medie
daca ![]() legatura este de intensitate puternica.
legatura este de intensitate puternica.
Formularea unor ipoteze cu privire la forma matematica a legaturii
Daca intre doua variabile (ambele cantitative !) se constata existenta unei legaturi de o anumita intensitate, ne punem problema posibilitatii modelarii legaturii printr-un model matematic. O prima etapa in acest demers este formularea unei ipoteze cat mai verosimile cu privire la forma legaturii. In acest scop, pe baza tabelului de corelatie construim norul statistic si linia poligonala a mediilor conditionate ale variabilei dependente.
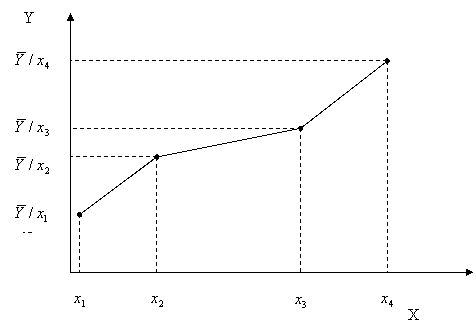
![]()
unde ![]() reprezinta functia de regresie care
aproximeaza cel mai bine forma legaturii, iar
reprezinta functia de regresie care
aproximeaza cel mai bine forma legaturii, iar ![]() o variabila aleatoare numita reziduala, care
insumeaza efectul altor factori decat cei luati in calcul.
o variabila aleatoare numita reziduala, care
insumeaza efectul altor factori decat cei luati in calcul.
5. Estimarea parametrilor functiei de regresie
Este o etapa care se succede firesc alegerii formei
functiei. In estimarea parametrilor va trebui sa tinem cont de abaterea
punctelor norului fata de modelul matematic ales ![]() , datorat
altor factori decat
, datorat
altor factori decat ![]() ,
considerati neesentiali, cuantificati prin variabila reziduala
,
considerati neesentiali, cuantificati prin variabila reziduala ![]() .
.
Principiul de la care se porneste in estimarea
parametrilor este cel al patratelor minime. Minimizam suma patratelor
abaterilor valorilor observate ale lui Y de la nivelul calculat prin ![]() . Conditia
de minim a sumei este echivalenta cu conditia de minim a mediei:
. Conditia
de minim a sumei este echivalenta cu conditia de minim a mediei:
![]() minima
minima
Ecuatia ![]() care descrie legatura dintre Y si
factorii de influenta
care descrie legatura dintre Y si
factorii de influenta ![]() se numeste ecuatia de regresie. Metoda
regresiei consta in modelarea legaturilor statistice prin ecuatia de
regresie.
se numeste ecuatia de regresie. Metoda
regresiei consta in modelarea legaturilor statistice prin ecuatia de
regresie.
Deoarece problema de minim se poate rezolva doar cunoscand forma particulara a functiei, vom aborda estimarea parametrilor seprat, pe tipuri de functii.
Regresia liniara
In ipoteza in
care legatura dintre Y si factorii sai de influenta ![]() este liniara, ecuatia de regresie va fi de
forma:
este liniara, ecuatia de regresie va fi de
forma:
![]()
Coeficientii ![]() se numesc parametrii modelului si vor rezulta
din minimizarea urmatoarei functii cu (n+1) necunoscute:
se numesc parametrii modelului si vor rezulta
din minimizarea urmatoarei functii cu (n+1) necunoscute:
![]()
Conditiile de
minim constau in anularea celor (n+1) derivate partiale ale functiei ![]() in raport cu necunoscutele
in raport cu necunoscutele ![]() , ceea ce
conduce la urmatorul sistem de ecuatii:
, ceea ce
conduce la urmatorul sistem de ecuatii:
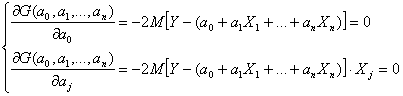
![]()
sau intr-o forma echivalenta:

![]()
de unde rezulta:
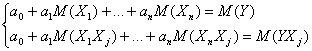
![]()
Prin
rezolvarea acestui sistem liniar de ecuatii in raport cu necunoscutele ![]() , se obtin
valorile parametrilor ecuatiei de regresie. Astfel, legatura statistica dintre Y
si
, se obtin
valorile parametrilor ecuatiei de regresie. Astfel, legatura statistica dintre Y
si ![]() este modelata prin aproximare cu o legatura
functionala. Pentru cazul cu doi factori
este modelata prin aproximare cu o legatura
functionala. Pentru cazul cu doi factori ![]() si
si ![]() , ecuatia
de regresie se scrie:
, ecuatia
de regresie se scrie:
![]()
iar sistemul de ecuatii devine:
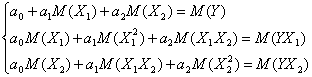
Prin
substitutia lui ![]() din prima ecuatie si inlocuirea lui in
celelalte, obtinem:
din prima ecuatie si inlocuirea lui in
celelalte, obtinem:
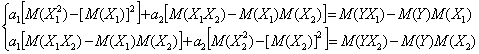
Daca pentru a aduce la o forma mai simpla notam cu:
![]()
care
reprezinta covariatia dintre variabilele ![]() si
si ![]() , obtinem:
, obtinem:
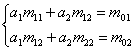
de unde putem obtine valorile parametrilor:
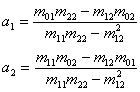
De aici il vom deduce si pe ![]() , care a
fost substituit in prima ecuatie. Astfel,
, care a
fost substituit in prima ecuatie. Astfel, ![]() sunt valorile parametrilor modelului liniar cu
trei variabile. Inlocuind valorile parametrilor in ecuatia de regresie se
obtine:
sunt valorile parametrilor modelului liniar cu
trei variabile. Inlocuind valorile parametrilor in ecuatia de regresie se
obtine:

Pentru a face relatia mai accesibila, introducem matricea de variatie si covariatie:
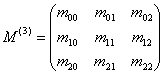
si notand
complementul algebric al elementului ![]() cu
cu ![]() ,
, ![]() ecuatia de regresie devine:
ecuatia de regresie devine:
![]()
Pentru cazul
mai general al legaturii liniare dintre Y si ![]() , matricea
de variatie si covariatie este:
, matricea
de variatie si covariatie este:
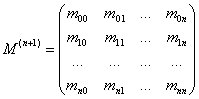
iar ecuatia de regresie se poate scrie:
![]()
Matricea de
variatie si covariatie ![]() este simetrica in raport cu prima diagonala.
Elementele
este simetrica in raport cu prima diagonala.
Elementele ![]() de pe diagonala principala sunt variantele
variabilelor
de pe diagonala principala sunt variantele
variabilelor ![]() , iar
elementele
, iar
elementele ![]() reprezinta covariantele dintre variabilele corespunzatoare.
reprezinta covariantele dintre variabilele corespunzatoare.
Regresia liniara simpla
In cazul regresiei liniare simple, cu variabila
endogena Y si factorul ![]() , matricea
de variatie si covariatie este:
, matricea
de variatie si covariatie este:
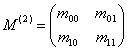
iar ecuatia de regresie devine:
![]()
de unde il
putem exprima pe ![]() ca:
ca:
![]()
de unde rezulta coeficientii:
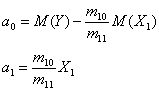
Regresia parabolica
In economie sunt numeroase exemplele in care legatura dintre fenomene si deci variabilele care le cuantifica nu este liniara. Daca Y reprezinta recolta la hectar dintr-un produs agricol, iar X cantitatea de ingrasaminte, ne vom da seama chiar si intuitiv ca o anumita crestere a lui X nu provoaca aceeasi crestere a lui Y pe tot intervalul de variatie al celor doua variabile. La valori mari ale cantitatii de ingrasaminte, acestea provoaca saturatie sau chiar nocivitate, ducand la o stagnare, respectiv diminuare a productiei. Alte exemple pot fi: legatura dintre vechimea in munca si marimea salariului, dintre cheltuielile cu publicitatea si volumul vanzarilor, etc.
Determinarea parametrilor functiei parabolice de regresie se poate face fie aplicand direct functiei metoda patratelor minime, fie prin reducerea la cazul liniar prezentat anterior. In ambele cazuri vom exemplifica pentru parabola de ordinul doi.
a) Estimarea parametrilor prin aplicarea directa a metodei patratelor minime
Ecuatia de regresie a modelului se scrie:
![]()
Din conditia de minimizare a expresiei:
![]()
avem urmatoarele egalitati:
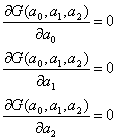
din care rezulta sistemul de ecuatii:
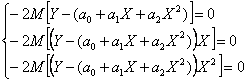
care este echivalent cu:
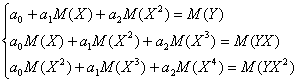
Rezolvand
acest sistem in necunoscutele ![]() , rezulta
parametrii ecuatiei de regresie parabolice. In mod asemanator se poate proceda
pentru orice regresie neliniara.
, rezulta
parametrii ecuatiei de regresie parabolice. In mod asemanator se poate proceda
pentru orice regresie neliniara.
b) Estimarea parametrilor prin reducerea la cazul liniar
Avand modelul parabolic de ecuatie:
![]()
facem substitutiile:
![]()
![]()
dupa care ecuatia devine:
![]()
care reprezinta un model liniar cu doi factori. Elementele matricei de variatie si covariatie vor arata astfel:
![]()
![]()
![]()
![]()
![]()
![]()
Problema regresiei neliniare pentru cazul unei parabole de gradul doi se reduce astfel la o problema de regresie liniara, care se rezolva conform cazului liniar. In cazul mai general, daca ecuatia de regresie este un polinom de gradul n:
![]()
efectuand substitutiile:
![]()
obtinem cazul liniar in raport cu (n+1) variabile.
Regresia exponentiala
Daca ecuatia de regresie are forma exponentiala:
![]()
se incearca aducerea la forma liniara. Mai intai se logaritmeaza ecuatia:
![]()
iar apoi se fac substititiile:
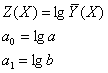
Rezulta astfel modelul liniar simplu:
![]()
Regresia hiperbolica
Daca ecuatia de regresie are forma hiperbolica:
![]()
se face substitutia:
![]()
de unde rezulta modelul liniar:
![]()
In matricea de variatie si covariatie elementele vor fi:
![]()
![]()
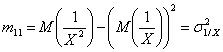
Alte tipuri de regresie
In practica economica se intalnesc frecvent si alte tipuri de functii (unele chiar functii compuse). Principiul de lucru pentru estimarea parametrilor va ramane insa intotdeauna acelasi: incercarea de a aduce functia la o forma liniara.
Foarte des intalnite sunt functiile de productie. Forma generala a acestora este:
![]()
Printr-o astfel de functie se defineste o legatura intre nivelul productiei Y si factorii de care aceasta depinde: productivitatea muncii, calificarea fortei de munca, gradul de inzestrare cu capital fix, etc. Determinarea parametrilor se face prin reducere la cazul liniar prin logaritmare:
![]()
Daca in aceasta noua ecuatie facem substitutiile:
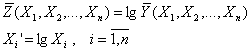
reducem ecuatia la una liniara multipla.
6. Analiza reprezentativitatii functiei de regresie
Coeficientul de corelatie
Constructia lui este similara cu a raportului de corelatie, cu deosebirea ca varianta in fiecare grupa este calculata folosind suma patratelor abaterilor fata de valorile ajustate prin functia de regresie si nu fata de media grupei. Ca urmare, coeficientul de corelatie va fi specific fiecarei functii in parte. Expresia lui de calcul (admisa aici fara demonstratie) este:
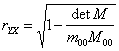
![]()
Interpretarea acestui coeficient in functie de valorile pe care le poate lua este urmatoarea:
daca ![]() functia nu este reprezentativa pentru
modelarea legaturii dintre variabile
functia nu este reprezentativa pentru
modelarea legaturii dintre variabile
daca ![]() functia are o reprezentativitate medie pentru
modelarea legaturii dintre variabile
functia are o reprezentativitate medie pentru
modelarea legaturii dintre variabile
daca ![]() functia este foarte reprezentativa pentru
modelarea legaturii dintre variabile
functia este foarte reprezentativa pentru
modelarea legaturii dintre variabile
Aceste limite nu trebuie interpretate foarte rigid. Valorile coeficientilor este bine sa fie comparate cu ale altor coeficienti, ai altor functii. Pentru aceeasi repartitie de exemplu, pentru functiile de regresie alese ca fiind posibilecalculam coeficientii de corelatie si il retinem pe cel mai mare, considerand acea functie ca fiind cea mai reprezentativa.
In cazul regresiei liniare simple, formula coeficientului poate fi adusa la o forma echivalenta mai simpla:
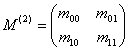
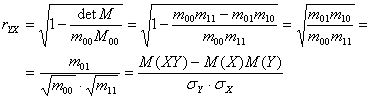
Prin corelatie simpla am studiat legatura liniara dintre doi factori neglijand influenta celorlalti factori, care actioneaza in acelasi timp asupra variabilei endogene. In corelatia multipla am masurat influenta simultana a doua sau mai multe variabile exogene asupra celei endogene. Ne punem insa problema de a masura influenta unei variabile independente asupra celei dependente, presupunand celelalte variabile la un nivel constant.
Fara a recurge la demonstratii, vom da modul de calcul al coeficientilor de corelatie partiala pentru doua cazuri:
a) Cazul unei variabile dependente Y si doua variabile independente X1 si X2:
- corelatia dintre Y si X1, neglijand influenta lui X2:
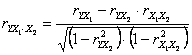
- corelatia dintre Y si X2, neglijand influenta lui X1:
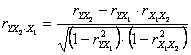
b) Cazul unei variabile dependente Y si trei variabile independente X1, X2 si X3:
- corelatia dintre Y si X1, neglijand influenta lui X2 si X3:
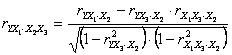
- corelatia dintre Y si X2, neglijand influenta lui X1 si X3:
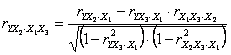
- corelatia dintre Y si X3, neglijand influenta lui X1 si X2:
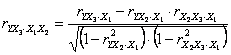
Aceste formule ale coeficientilor de corelatie partiala se pot generaliza si pentru cazul a k variabile independente.
Probleme propuse
Problema 1
Cunoastem urmatoarea distributie a 52 de societati comerciale cu acelasi profil de activitate, in raport cu variabilele X - cheltuielile cu publicitatea (mil. lei) si Y - volumul vanzarilor (mil. lei).
|
X Y |
Total |
|||
|
Total |
Se cere:
Pe baza unui grafic adecvat sa se emita ipoteze privind forma posibila a functiei de regresie.
In ipoteza unei forme liniare a dependentei dintre Y si X, sa se calculeze parametrii functiei de regresie.
Sa se studieze reprezentativitatea functiei de regresie pentru modelarea legaturii dintre cele doua variabile.
Care este valoarea medie a volumului vanzarilor pentru un nivel al cheltuielilor cu publicitatea de 55 milioane lei ?
Aceleasi cerinte de la punctele 2, 3 si 4 pentru o forma parabolica a dependentei dintre Y si X.
Problema 2
Un produs a fost lansat simultan pe 13 piete. Pe aceste piete, produsul a fost propus la preturi diferite (P), veniturile consumatorilor (V) fiind si ele diferite. Pentru fiecare piata s-a inregistrat un anumit nivel al cererii (C), rezultatele fiind sintetizate in tabelul urmator:
|
Nr. crt. |
Cerere (C) |
Pret (P) |
Venit (V) |
Se cere:
1) Sa se formuleze ipoteze cu privire la forma legaturii dintre cerere (C) si pret (P). Pentru formele functiilor de regresie retinute ca fiind posibile, sa se calculeze parametrii functiilor si reprezentativitatea acestora.
2) Similar pentru legatura dintre cerere si venit.
3) Sa se calculeze parametrii functiei care modeleaza legatura liniara multipla dintre cerere si factorii sai e influenta. Analizati reprezentativitatea acestei functii in raport cu reprezentativitatea functiilor de regresie simple. Care va fi valoarea estimata a cererii pe o piata unde pretul de vanzare va fi 3,2 iar venitul mediu al consumatorilor de 550 ?
Bibliografie:
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 5086
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved