Parametrii formei

Parametrii formei

Din aplicatiile practice, precum si din alte surse, s-au constatat ca graficele pot avea diverse forme, dintre care: forma de coplot, forma de U, J, L sau alte forme. Ceea ce prezinta importanta, nefiind surprins de nici un parametru prezentat, il constituie modul de repartizare a valorilor variabilei de o parte si de alta a valorii medii, considerata si centrul de greutate a seriei. Acest lucru nu inseamna altceva decat evidentierea acelei curbe care aproximeaza cel mai bine conturul poligonal al seriei respective si in acelasi timp o imagine mai clara asupra gradului de reprezentativitate a valorii medii.

In marea majoritate a cazurilor, distributia unitatilor unei populatii se face dupa un clopot (dupa legea normala a lui Gauss). Dar unitatile nu se distribuie uniform in jurul valorii medii, ceea ce poate conduce la inclinatii intr-o directie sau alta a valorii medii. Aceasta distribuire neuniforma poate conduce la cazul cand diferite serii (diferit distribuite in jurul valorii medii) sa aiba aceeasi medie, acelasi σ si totusi o curba sa fie mai aplatizata decat cealalta, simetrica sau mai putin simetrica. Evidentierea acestor diferente poate fi realizata cu ajutorul parametrilor formei.

Parametrii formei unei serii de repartitie, dupa continut, se clasifica in doua grupe:

parametrii asimetriei;

parametrii boltirii.

1. Parametrii asimetriei

Asimetria unei serii se defineste in raport cu dispunerea unitatilor intr-o parte sau alta a valorii medii.

In acest sens, o serie de repartitie este simetrica in raport cu media sa daca frecventele valorilor variabilei X egal departate de valoarea medie sunt egale intre ele, adica:

oricare ar fi δ astfel incat si sa se afle printre valorile lui X.

Coeficientul de asimetrie al lui Fisher

Acest parametru se noteaza cu α₃, iar expresia sa de calcul este:

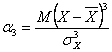(2.47)

sau intr-o forma echivalenta:

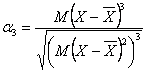
Calculand valoarea acestui parametru, in functie de semnul ei, avem urmatoarele cazuri:

1. α ₃ = 0, ceea ce inseamna ca = 0, adica suma tuturor abaterilor cu semnul minus este egala cu suma tuturor abaterilor cu semnul plus, ridicate la puterea a treia. Ca urmare in acest caz se poate spune ca seria este simetrica.

2. α ₃ > 0, ceea ce inseamna ca > 0. Aceasta este echivalent cu faptul ca pe total suma abaterilor cu semnul plus de la valoarea medie este mai mare decat suma abaterilor cu semnul minus si ca urmare seria prezinta o asimetrie pozitiva.

3. α ₃ < 0, deci < 0. Aceasta inseamna ca pe total, suma abaterilor cu semnul minus este mai mare decat suma abaterilor cu semnul plus de la valoarea medie. O astfel de serie se spune ca reprezinta o asimetrie negativa.

2. Parametrii boltirii

Aprecierea boltirii unei serii este utila in caracterizarea gradului de reprezentativitate a valorii medii cat si pentru compararea reprezentativitatii a doua sau mai multe valori medii ce reprezinta serii diferite.

Parametrul da o caracterizare numerica sub forma absoluta a gradului de boltire a unei serii. Sub forma relativa, gradul de boltire se masoara cu parametrul:

(2.48)

Pentru a intelege semnificatia boltirii unei serii, se considera doua serii statistice care au la baza variabilele X si Y, iar

Mai presupunem, in plus, ca cele doua distributii au forma de clopot pentru care α _3X = α _3Y , adica ambele sunt simetrice. Desi s-ar parea ca cele doua serii nu au nimic care sa le deosebeasca, totusi reprezentandu-le grafic rezulta doua curbe de forma:

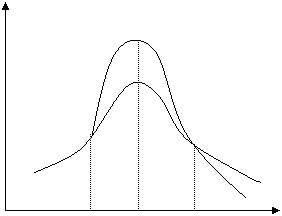
X

Y

unde graficul lui X este mai inalt, iar al celeilalte mai plat. Ca urmate, se observa ca cele doua serii nu sunt caracterizate de aceeasi boltire.

Boltirea unei serii este utila pentru a da o caracetrizare mai exacta reprezentativitatii valorii medii.

In cazul exemplului prezentat mai sus, atat mediile cat si abaterile medii patratice sunt egale si ca urmare, coeficientul de variatie al lui Pearson este acelasi pentru cele doua serii. Deci rezulta ca ambele valori medii prezinta acelasi grad de reprezentativitate. Cu toate acestea, graficele celor doua serii contrazic concluzia dedusa in urma compararii celor doi coeficienti de variatie.

Valoarea medie cea mai reprezentativa in seria in care cele mai multe unitati ale populatiei cercetate au inregistrat valori, mai apropiate de valoarea medie. Pentru o astfel de serie, imprastierea fata de valoarea medie fiind mica, graficul are o forma mai ascutita in cazul seriei X si mai plata in cazul seriei Y.

Nivelul boltirii pentru o serie oarecare data se masoara cu ajutorul parametrului B₄, a carui expresie de calcul este data de relatia (2.48). Valoarea lui B₄ pentru o distributie normala este egala cu 3. Pentru orice alta curba corespunzatoare unei serii date si aproximata cu un clopot, raportul intre momentul centrat de ordinul patru si patratul momentului centrat de ordinul al doilea, este un numar diferit de 3, curba respectiva fiind mai ascutita sau mai plata decat curba normala a lui Gauss.

Comparand gradul de boltire al unei serii oarecare si gradul de boltire al clopotului lui Gauss, Fisher a stabilit urmatoarea expresie de calcul al coeficientului boltirii, notat cu B₄^':

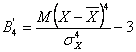sau: B₄^' = B₄-3

expresie cunoscuta in literatura de specialitate sub denumirea de exces al seriei.

Urmatoarele cazuri sunt semnificative cu privire la aprecierea boltirii unei serii:

- daca B₄^' =0 (adica B₄ = 3) atunci seria in cauza prezinta aceeasi boltire cu a curbei normale (excesul este nul);

- daca B₄^' > 0 (adica B₄ > 3) atunci boltirea corespunzatoare curbei respective este mai inalta si mai ascutita decat curba normala (serie leptokurtica);

- daca B₄^' < 0 (adica B₄ < 3) atunci boltirea corespunzatoare curbei respective este mai plata (mai joasa si mai larga) decat curba normala (serie platikurtica).

Asimetria si boltirea joaca un rol insemnat in caracterizarea formei unei serii atributive de repartitie. Cu ajutorul parametrilor prezentati poate fi formata o imagine mai clara asupra unei serii deja construite, asupra masurii in care seria respectiva poate fi reprezentata de valoarea sa medie.

Bibliografie

Buiga, A., Metodologie de sondaj si analiza datelor in studiile de piata, Ed. Presa Universitara Clujeana, Cluj-Napoca, 2001;

Buiga, A., Dragos C., Lazar D., Parpucea I., Todea A., Statistica I, Ed. Presa Universitara Clujeana, Cluj-Napoca, 2003;

Florea I., Parpucea I., Buiga A.,    Statistica descriptiva, Ed. Continental,

Cluj-Napoca, 1998