ECOLOGIA POPULATIEI (ECOLOGIA SPECIEI) - concepte, particularitati, caracteristici

Facultatea de Stiinta mediului

Ecologie generala

An II, Sem. 1

Ecologia populatiei

(ecologia speciei)

1. Specia si populatia - concepte, particularitati, caracteristici

1.1. Specia - unitatea a sistematicii si unitate functionala a ecosistemului

Specia este unitatea fundamentala a sistematicii, o unitate functionala alcatuita din indivizi de origine comuna care realizeaza un travaliu geochimic si o anumita functie pe o suprafata numita areal si unde sunt localizate populatiile sale.

La fel ca si organismul, specia este caracterizata de potential bioecologic (capacitatea speciei de a ocupa habitate si nise noi, de a evolua si de a rezista variatiilor factorilor de mediu prin realizarea homeostaziei). Despre speciile capabile de a ocupa nise ecologice noi spunem ca au plasticitate ecologica mare. Am evidentiat, de asemenea, la nivelul organismului ca o expresie a potentialului ecologic este valenta ecologica (masura eficientei speciei fata de variatiile factorilor de mediu) (de ex. ulmul american este plantat pe marginea apelor in Delta Dunarii si el rezista gerurilor foarte puternice, vanturilor si revarsarilor de ape; spunem ca are o valenta ecologica mare; ariciul nu poate rezista la temperaturile scazute din iarna si este nevoit sa hiberneze, el are o valenta ecologica scazuta).

Ca si in cazul organismului, diferentierea speciilor potrivit potentialului bioecologic provoaca aparitia a doua tipuri fundamentale de reactie fata de variatiile factorilor de mediu: euribioza (reactia de maxima rezistenta a speciei fata de variatiile factorilor de mediu, are o toleranta larga si suporta variatii largi ale acestora fara pierderea nisei ecologice ocupata in ecosistem) si stenobioza (reactia de minima rezistenta a speciei fata de variatiile factorilor de mediu, toleranta ingusta, suporta variatii inguste ale acestora si pierd nisa ecologica avuta in ecosistem, atunci cand variatiile factorilor de mediu depasesc limitele de toleranta ale speciei).

Rezultat al interactiunii permanente dintre organism sau organisme cu mediul se remarca ecologic, doua trepte de diferentiere a speciilor:

☻ - ecotipul (cuprinde un grup de indivizi care se deosebesc de alti indivizi ai aceleiasi specii, prin nisa ecologica, habitat sau microhabitat ocupat, proprietati biologice si structura genetica; in ecologia plantelor se foloseste termenul de ecotip, sinonim cu soiul din agrobiologie, iar in ecologia animala cel de rasa ecologica)

☻ - ecospecia (este o treapta mai profunda a diferentierii ecologice a speciilor, constand in deosebiri de nisa ecologica intre specii, corelat cu deosebiri morfologice, biologice si comportamentale pregnante; daca luam o specie de planta care traieste in mai multe habitate, se va constata ca existe diferente morfologice evidente, asa cum ar fi de exemplu marimea si forma frunzelor; la o specie animala pot sa existe sau nu diferente morfologice, dar in schimb pot aparea diferente biologice sau comportamentale

1.2. Populatia si mediul de viata al populatiei

Populatia este un sistem alcatuit din indivizi de origine comuna, din aceeasi specie, purtatori ai unei functii specifice, alcatuind o unitate functionala si reproductiva, atasata la un anumit biotop (fragment de spatiu populat si transformat de catre organismele vii).

Populata reprezinta nivelul supraindividual de organizare a materiei vii, alcatuita dintr-un numar variabil de indivizi care apartin aceleiasi specii, organisme care se diferentiaza sub raport genotipic si fenotipic si formeaza grupuri de indivizi.

Populatia se refera la un grup de indivizi ai aceleiasi specii aflat intr-o relativa izolare teritoriala fata de alte grupuri de indivizi, formeaza o unitate naturala de existenta, de adaptare, de stabilitate si evolutie a speciei in arealul respectiv (Tufescu si Tufescu, 1981).

Populatia este o parte concreta a biocenozei cuprinzand indivizi ai aceleiati specii cu o functie specifica in ecosistem (Stugren, 1965).

Pentru ecologi este important de inteles care sunt fenomenele naturale care determina marimea si componenta populatiei de plante sau de animale si mai ales ce schimbari pot avea loc sub influenta factorilor de mediu. Au fost evidentiate corelatii ale abundentei si schimbarii populatiei de organisme cu vremea (Davidson si Andrewartha, 1948). In studii experimentale in conditii de laborator s-a evidentiat ca temperatura si umiditatea au influentat rata intrinseca a cresterii naturale (Birch, 1953). De asemenea, studii efectuate in conditii de laborator asupra unor populatii a evidentiat o buna legatura (dependenta) la un model logistic de dezvoltare. Alte studii au evidentiat modelele de fluctuatie a populatiilor in conditii naturale.

Modelul de distributie a populatiilor (speciilor) sunt limitate de factorii fizici (abiotici) de mediu (umiditate, lumina, temperatura, pH, solul, apa etc. Populatia fiind un grup de indivizi, exista un model organismal de dezvoltare in relatie cu factorii de mediu (Fig. 5-1), dezvoltarea speciei insciindu-se in limita de toleranta ca euritopica sau stenotopica, ilustrind un interval optim si un maxim caracteristic.

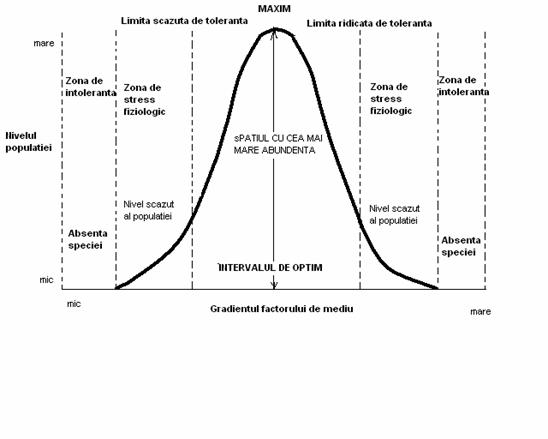
Fig. 5-1. Modelul de distributie a organismului in relatie cu mediul fizic (valenta ecologioca) (dupa Cox si colab., 1976; Stiling, 1996).

In natura, in cazul competitiei dintre specii o anumita specie poate "ocupa" un interval optim al altei specii (sau o parte din el), fenomen ilustrat si in conditii de laborator, dar in absenta competitiei (Fig. 5-2). Astfel, fiecare specie are un optim ecologic, iar in conditii de laborator s-a pus in evidenta un optim fiziologic care la unele specii se poate suprapune peste optimul ecologic din natura.

Arealul populatiei (populatiilor). In functie de extindere si delimitare biocenotica, populatiile pot fi: geografice (delimitate de arii geografice distincte), ecologice (sunt populatii cenotice care apartin aceleiasi biocenoze) si elemntare (care sunt parti ale populatiilor ecologice).

In studiile ecologice apar o serie de dificultati in ceea ce priveste definirea arealului unei populatii deci precizarea teritoriului pe care il ocupa. Se fac frecvente confuzii si azi atunci cand se face raportarea la o anumita specie studiata ecologic in camp si se spune "populatia speciei X" sau "populatiile speciei X". Tufescu si Tufescu (1981) referinduse la populatii de pastrav si populatii de harciog fac referire la inegalitatea populatiilor raportat la marimea suprafetelor pe care le ocupa. Cercetari ecologice de lunga durata efectuate in zona Cluj au evidentiat modelul comportamental al spciei mamestra brassicae. Studiul dinamicii populatiilor, distanta de zbor, modelul de comportament, rspunsul populatiilor izolate geografic la feromonul sexual specific etc, au evidentiat existenta populatiilor izolate geografic. Marimea unei populatii locale este in functie de: uniformitatea formelor de relief; comportamentul trofic; nivelul de dependenta de tipul si cantitatea plantei gazda; capacitatea si comportamentul de zbor; marimea speciei; speciile competitive; simpatrice sau cohabitante; daunatori si boli; valoarea si amplitudinea de variatie a factorilor fizici si biotici de mediu; feromonul sexual natural (Stan si colab., 1987; Stan si colab., 1994; Stan, 1996, 1998).

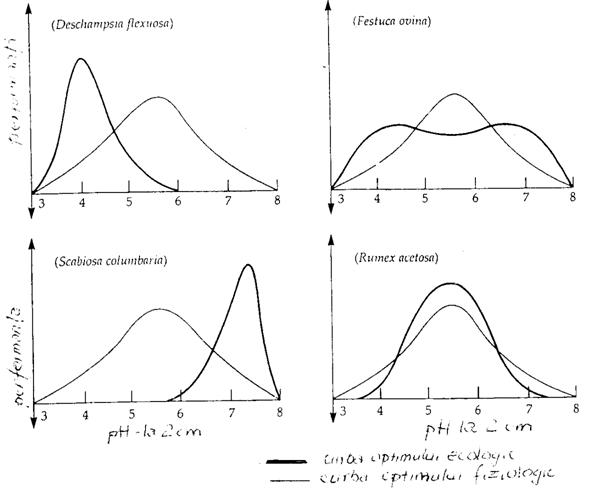
Fig. 5-2. Performantele a 4 specii de plante in functie de valoarea pH-ului din sol si evidentierea trendului curbei optimului ecologic din natura si a optimului fiziologic, in conditiile experimentarii in laborator (dupa Callinson, 1977; din Stiling 1996)

Dupa cum se stie, nu exista indivizi biologici izolati, separati, care sa nu apartina unei specii. In areal insa specia este reprezentata de populatie sau populatii. In unele situatii (specii nou introduse in habitat, specii pe cale de disparitie, specii din teritorii insulare etc), specia poate fi reprezentata printr-o singura populatie, situatie in care specia si populatia se confunda. Pe de alta parte, nu va exista nici o specie care sa nu fie reprezentata de cel putin o populatie, indiferent de marimea acesteia.

Marimea populatiei si numarul de populatii, raportat la teritoriul pe care o populatie il acopera este in functie de tipul de specie. Exista diferente in ceea ce priveste teritoriu la o specie de urs, o specie de lumbricid si o specie de insecta. Daca sunt conditii optime si uniforme pe o suprafata mare de areal (ex. depresiune) eventual definim o populatie geografica. In conditii in care acea suprafata este strabatuta de unitati mai mici de relief (vai, coline etc) este necesar de precizat daca ceea ce noi studiem este o populatie ecologica sau una elementara. Una sau mai multe.

Gruparea indivizilor populatiei, modelul de distributie a populatiilor, marimea populatiilor, dinamica populatiilor sunt o serie de indicatori care definesc particularitatile speciei studiate.

Elementele de carecterizare ale staticii populatiei (ciclul biologic, densitatea, cresterea, marimea, longevitatea, supravietuirea) sunt de asemenea deosebit de importante.

2. Organizarea si functionarea sistemelor de tip populatie

2.1. Integralitatea sistemului de tip populatie

Botnariuc (1976) arata ca nu exista o conceptie unica si unitara referitoare asupra populatiei (speciei). Sunt cercetatori care nu fac similitudine intre cele doua concepte ecologice; unii cred ca nici nu se poate vorbi de un nivel de organizare ca specie sau populatie; altii considera ca doar populatia are un nivel de organizare sistemic si nu specia.

Exista puncte de vedere ale unor cercetatori care nu considera specia sau populatia ca un sistem ecologic pe considerentul ca specia nu este o unitate ecologica ci una genetica. Realitatea este insa certa: specia este o entitate genetica si ecologica.

In capitolul anterior an analizat organizarea si functionarea sistemului de tip individual (organismul). In cazul acestuia, integralitatea este clara, dovedita de studii morfologice, anatomice, fiziologice, embriologice, etologice. Prin comparatie cu individul, specia pare a nu dispune de aceasta caracteristica a sistemului biologic, deoarece ea este constituita de indivizi diferiti (dar asemanatori si inruditi), izolati unul de altul, cu capacitate de deplasare (uneori pe distante mari) in portiunea de areal in care traiesc. Specia nu este la fel de evidenta ca sistem integral dar intruneste caracteristicile de functionare ale unui sistem biologic. Ea este rezultat al unei heterogenitati structurale si functionale si al diferentierii intraspecifice, ce duce la aparitia si consolidarea relatiilor intraspecifice, in constituirea partilor in intreg (Botnariuc, 1976).

Cercetatorii au identificat o diversitate a grupelor de indivizi (impuse de bariere de naturi diferite) si o diversitate a organismelor din interiorul unei grupe de indivizi. Diversitatea intraspecifica, expresie a integralitatii speciei este asadar dependenta de variabilitatea sistemelor individuale, pe de o parte, si de amplitudinea fiecarei variatii individuale, pe de alta parte.

Variabilitatea afectand toti indivizii populatiei este un fenomen populational, o caracteristica a populatiei, considerata ca intreg, deci altfel spus este o caracteristica si a integralitatii populatiei. Fiind o insusire a populatiei (speciei) se cauta exemplificarea limitelor intre care se produce variabilitatea, cauzele care o determina si amplitudinea atinsa. Variabilitatea diferitelor caractere se inscrie in limite specifice, deci caracteristice si fiecarei populatii. Studii autecologice in conditii de laborator la specii de lepidoptere daunatoare, au evidentiat ca stadiul larvar de exemplu se antinde pe un interval larg, inregistrand un interval de variabilitate al greutatii indivizilor chiar daca au provenit din aceeasi ponta. In cresterea de generatii succesive se poate reduce acest interval prin operatiuni de selectie artificiala (Stan si colab., 1997; Stan si colab., 1998). Probabil ca in conditiile din cimp aceasta variabilitate este si mai mare. Asadar, exista variatii individuale mai mult sau mai putin pronuntate, dar la nivel de populatie ele pot fi atenuate prin mecanismele selectiei.

Studiul ciclului de viata la multe specii pune in evidenta corelatii complexe intre durata stadiilor si calitatea mediului sau modelul comportamental, o reala interdependenta intre mediu, comportament si ciclul biologic. Toate aceste interrelatii nu sunt trasaturi ale indivizilor izolati ci ale speciei (populatiei) ca intreg, ceea ce este expresia integralitatii speciei. Numarul de indivizi si complexitatea relatiilor dintre acestia si dintre ei si mediu reprezinta una din cele mai importante adaptari ale populatiei considerata un intreg, un sistem functional.

2.2. Populatia - sistem autoreglabil

Din moment ce am aratat ca populatia este un sistem biologic, integralitatea si echilibrul sau pot fi mentinute prin mecanisme de autocontrol, deci prin autoreglare. Mecanismele autoreglarii sunt variate si caracteristice fiecarei specii, dar in esenta, autoreglarea depinde atat de factori interni cat si de factori de mediu externi. Autoreglarea inseamna relatie stransa, interconexiune, cu mediul

Autoreglarea este o adaptare la mediu si ca orice fenomen de acest tip ea este relativa, deci mentine integralitatea populatiei (speciei) intre anumite limite. Peste aceste limite pot apare dezechilibre.

Exista diverse modalitati prin care se realizeaza autoreglarea si toate se reflecta in marimea unei populatii, numarul de populatii si structura lor, de la mecanismele si caile biologice (marimea, numarul si durata stadiilor, reproducere, prolificitate etc) la cele comportamentale (hranire, zbor, locomotie, migrare etc) la cele modelate de mediatori chimici (allomoni, kairomoni, sinomoni, feromoni epideictici, feromoni sexuali, feromoni de agregare, feromoni sociali etc).

2.3. Populatia si selectia naturala

Populatia este o grupare de indivizi. Individul este un subsistem al sistemului pe cale l-am numit - populatie. Astfel conform teoriei sistemelor, el este subordonat populatiei, in sensyul ca trasaturile morfologice, functionale, comportamentale ale fiecarui individ sunt reflectate in structura si functionarea populatiei. Privit in acest fel, fiecare trasatura a individului (organismului) este rezultatul evolutiei populatiei (speciei). Am amintit anterior ca prin selectia artificiala putem modela variabilitatea organismelor in cadrul populatiei. Trebuie precizat insa ca selectia artificiala actioneaza asupra genotipului. In conditii naturale actioneaza selectia naturala. Ea se manifesta numai asupra fenotipului, iar prin acesta si asupra genotipului. Mai mult, selctia naturala nu actioneaza asupra caracterelor fenotipice izolate ci a tuturor trasaturilor fenotipice (compatibile cu existenta individului si utile populatiei).

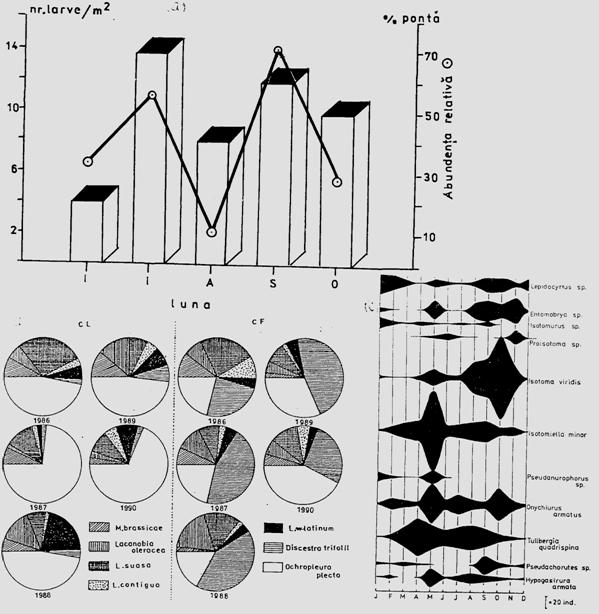
Fig. 5-3. Reprezentarea grafica a frecventei, abundentei relative si densitasii cu ajutorul histogramelor sau a curbelor de variatie (dupa Stan si Coroiu, 1978; Stan, 1993). (a). densitatea si abundenta relativa a larvelor de Mamestra brassicae pe durata a 5 luni intr-o cultura de varza; (b). abundenta relativa a 7 specii de lepidoptere ilustrata sectorial pe baza datelor de captura din capcane feromonale si capcane luminoase din zona Cluj (1986-1990); (c). densitatea speciilor de colembole dominante dintr-o cultura de lucerna din zona Cluj.

Prin caracteristica structurala si functionala a populatiei, selectia naturala a devenit o legitate caracteristica unui sistem de tip populatie. Trasaturile structurale si functionale elaborate si perfectionate ca rezultat al selectiei naturale, vor avea ulterior o influenta considerabila asupra selectiei influentand mersul acesteia. Selectia intraspecifica (determinata de relatiile intraspecifice, un "program pentru populatie", care regleaza numarul si densitatea organismelor) si selectia ectospecifica (determinata de relatiile interspecifice, de precizare a locului si rolului populatiei in cadrul biocenozei si implicit a ecosistemului) sunt doua forme care se intrepatrund deoarece si intre factorii interni (natura speciei, marimea populatiei, tipul de reproducere) si factorii externi exista corelatii si interconditionare.

3. Structura populatiei (statica populatiei)

3.1. Distribuirea caracterelor demografice. Descrierea populatiei. Evaluari cantitative ale populatiei

La nivelul unei populatii se pot defini o serie de procese globale: crestere, dezvoltare, reproducere (multiplicare), longevitate, supravietuire, relatii comportamentale, raporturile dintre organisme (interrelatii, reactii, coactii etc), repartitia indivizilor in cadrul populatiei si in mediul de viata etc.

Unul din aspectele importante este distributia caracterelor demografice, cu referire la clase de varsta, la raporturi de abundenta intre indivizi, la stadii si forme de dezvoltare, abundenta totala etc. Facand referire la terminologia de distributie, aici ea se refera la sensul statistic (distributie de frecvente si probabilitati). In spatiu, in mediul in care traiesc, organismele manifesta comportamentul de repartitie (in limba engleza nu exista doi termeni pentru distributie, dar in l. franceza de ex. se precizeaza acest lucru de fiecare data: distributia frecventelor sau distributie in spatiu si timp).

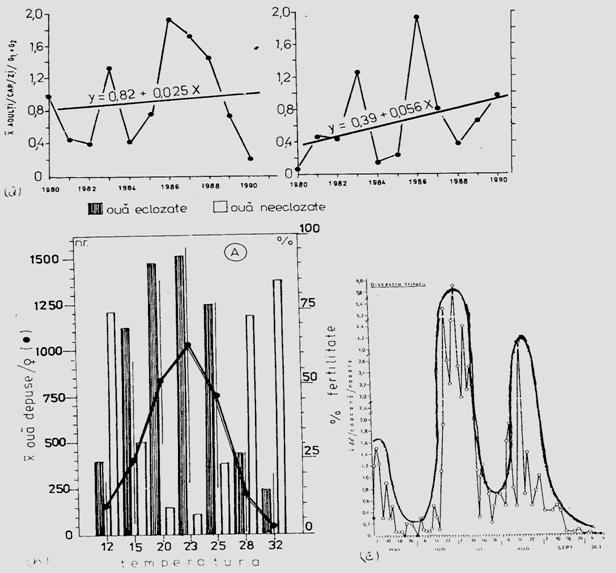
Fig. 5-4. (a). Model teoretic de curba reala si curba teoretica ilustrind tendinta de evolutie a populatiei locale de Mamestra brassicae din zona Floresti-Cluj. (b). Curba reala unimodala si poligon de frecventa ilustrand fecunditatea femelelor de Mamestra brassicae si fertilitatea pontei, in relatie cu temperatura. (c). Curba reala polimodala (aici doar cu 3 "varfuri" = maxime), pentru specia Discestra trifolii (Lepidoptera: Noctuidae) (dupa Stan, 1990, 1994).

In studii ecologie, autecologice sau sinecologice, este absolut necesar a analiza complex populatia sau populatiile componente ale biocenozelor, situatie in care indivizi pot fi distribuiti pe clase de frecventa, dupa abundenta relativa sau ca densitate, iar pentru vizualizare se folosesc reprezentari grafice diverse: histograme, curbe de variatie etc. Curbele pot fi reale si teoretice (Fig. 5-3; 5-4).

Analiza populatiilor este necesar sa includa date referitoare la: numarul si marimea generatiilor, clasele de varsta, cohortele, stocurile, ecofaza etc.

(in limba fr. exista termenul de peuplement ce semnifica un ansamplu de populatii de specii diverse care exista pe acelasi teritoriu; termenul clasic de populatie este diferit de acesta; Barbault, 1992, da termenului de peuplement un sens restrictiv = "ansamblu plurispecific definit in functie de problemele studiate" si nu sensul de simpla grupare de specii = association, assemblage; in limba engl. nu exista acest aspect; peuplement este diferit de communautes - comunitatile = biocenozele; cohorta = ansamblu de indivizi nascuti in acelasi timp, sau la interval scurt unul fata de altul si in acelasi teritoriu; este o notiune complementara clasei de varsta; uni pun echivalenta intre cohorta si generatie dar aceeasi generatie poate da nastere la mai multe cohorte; ecofaza = intervalul unde specia traieste in acelasi biotop si are acelasi regim alimentar, adica ocupa aceeasi nisa ecologica; stocul este o unitate subspecifica si se intelege ca o parte din populatie).

Pe baza datelor de esantionaj (sampling), populatiile se pot caracteriza complex, la nivel de indivizi si la nivel de populatie.

Descrierea indivizilor si populatiilor. La nivel de individ intereseaza numarul (cantitatea), ciclul biologic, marimea (talia), varsta, biomasa. Exista modalitati concrete cu posibilitate de numarare, masurare-cantarire, sau indirect, prin metode statistice de corelatie (ex. corelatie greutate - marime). Asemenea corelatii se fac in cazul speciilor de dimensiuni mici. In ceea ce priveste varsta, in conditii naturale, aceasta este greu de precizat. Se determina cu precizie in studii autecologice, in conditii de laborator si ulterior se pot face analogii cu situatiile din natura dupa operatiile de sampling si prelucrarea si determinarea materialului biologic,. Si in acest caz, in situatii deosebite, se pot face corelatii matematice (ex. talie - varsta).

Toate operatiile si evaluarile care se fac asupra populatiilor se bazeaza pe "informatia" oferita de planul de esantionare. In ecologie el reprezinta elementul esential de care depinde corecta analiza a populatiilor din ecosisteme.

Exista aici o serie de aspecte de detaliu cu semnificatie deosebita, cel mai important fiind legat de succesiunea logica a etapelor de lucru [ex. studiul ecosistemului, analiza habitatelor, biocenozelor si a speciilor reprezentative, alegerea campului experimental = stationar, fixarea tipului de probe ce trebuie prelevate (pe baza relatiei numarului optim de probe), alegerea metodei specifice, intocmirea sirului de date initiale, operatii asupra sirului (eliminarea valorilor aberante, normalizarea datelor, transformarea datelor, vizualizarea preliminara), operatii matematice-statistice asupra valorilor obtinute (medii, indici statistici, variatii, indici ecologici), reprezentari grafice, analize si sinteze, modalare matematica, actiuni parctice etc].

1. Evaluarea numarului indivizilor (abundenta)

☼ - Analizele semi-cantitative. In acest caz, cand anumite caractere nu pot fi masurabile, se fac de asemenea corelatii matematice. Asa este de exemplu scara de abundenta-dominanta pentru studiul covorului vegetal (scoala fitosociologica Braun-Blanquet), care a stabilit urmatoarele 6 trepte:

- acoperire pe o suprafata mai mare de ;

- acoperire de la la din suprafata;

- acoperire de la la din suprafata;

- acoperire de la 1/20 la din suprafata;

- indivizi destul de numerosi dar grad de acoperire slab;

- indivizi rari sau foarte rari.

Cotatia abundentei pentru zooplancton. Aici clasele de abundenta sunt ales in progresie geometrica:

- 1-4 indivizi/proba (specie foarte rara);

- 4-18 indivizi/proba (specie rara);

- 18-80 indivizi/proba (specie destul de rara);

- 80-350 indivizi/proba (specie destul de numeroasa);

- 350-1500 indivizi/proba (specie numeroasa);

- 1500-6500 indivizi/proba (specie foarte numeroasa)..

Alte asemenea scari se estimeaza procentual, se construiesc simboluri de reprezentare cu care se vizualizeaza.

☼ - Analizele cantiative (vezi Lucrarile practice

a. Numarul indivizilor (A b u n d e n t a . In cazul analizelor cantitative se apreciaza numarul sau biomasa indivizilor din populatie. In acest caz se face numararea indivizilor si se apreciaza cat de multi sunt. Se poate evalua prin metode speciale si marimea unei populatii locale

b. D e n s i t a t e a (abundenta numerica) Toate organismele vii sunt constituite in grupuri ale aceleiasi specii (populatii). Aceste populatii ocupa un spatiu particular, au o densitate si structura de varsta, o rata a nasterii si una a mortalitatii, o forma de crestere si o dispersie in timp si spatiu. Marimea populatiei in relatie cu o unitate definita de spatiu reprezinta densitatea populatiei.

c. A b u n d e n t a r e l a t i v a. Reprezinta exprimarea in precente (%) sau in probabilitati, a participarii fiecarei specii in populatia sau biocenoza studiata.

Nefiind de fel usor in a aprecia abundenta unor specii de animale, mai ales nevertebrate (ex. insecte) se foloseste frecvent, si in acest caz, metoda botanica a claselor de abundenta, marcate prin semne conventionale. Reprezentarea grafica poate fi de asemenea sugestiva..

d. F r e c v e n t a. Reprezinta % de indivizi ai unei specii in raport cu numarul total de indivizi. Ea poate fi calculata si pentru o proba sau mai multe probe, extrase dintr-o populatie sau o biocenoza. Altfel spus, frecventa reprezinta proportia in care o specie apare intr-un anumit numar de probe.

Prin prelucrarea datelor se vor alcatui apoi histograme de frecventa care vizualizeaza situatia dintr-o biocenoza, comparativ cu altele. In aceste situatii se stabilesc relatii intre frecvanta generala - frecventa absolut- frecventa relativa, dupa exemplul din Tabelul Se intalnesc 3 situatii distincte:

- in biocenoza, speciile care o alcatuiesc sunt putin numeroase si frecventele lor sunt diferite;

- speciile din biocenoza sunt reprezentate mai mult sau mai putin egal, iar frecventele lor sunt asemanatoare;

- una sau mai multe specii sunt numeroase, ele alcatuind cea mai mare parte a faunei, deci frecventele vor apare foarte asimetrice.

Tabelul 5

Reprezentarea ipotetica a unui tip de relatie intre frecventa generala, frecventa absoluta si frecventa relativa

e. C o n s t a n t a La nivelul studiului faunei, este legata de prezenta speciei in una sau mai multe biocenoze, deci ea este evaluata in functie de valorile frecventei.

In functie de valorele lui c s-au stabilit 4 categorii de specii:

- c < 25% = specii accidentale

- c =225,1 - 50% = specii accesorii

- c = 50,1 - 75% = specii constante

- c > 75% = specii euconstante.

(in botanica exista 5 clase si este putin diferit).

f. D o m i n a n t a. In cazul animalelor, dominanta exprima influenta exercitata de o specie intr-o comunitate sau se mai spune ca dominanta evidentiaza rolul speciei in transportul materiei si energiei in ecosistemul studiat. Daca abundenta speciei = densitatea, atunci dominanta = suprafata ocupata. Deci, dominanta este o notiune care nu poate fi evaluata cantitativ. Dominanta se poate exprima in interiorul unui grup de organisme sau se raporteaza la o intreaga biocenoza. Se poate spune ca dominanta se confunda cu abundenta, dar sunt situatii cand o specie poate fi putin abundenta insa exercita o influenta mare in biocenoza si invers, o specie este abundenta, dar influenta ei este redusa. Desi nu poate fi evaluata direct, cantitativ, dominanta poate fi ilustrata cu ajutorul unor indici specifici (vezi lucrarile practice).

Descrierea staticii populatiei. La acest nivel este importanta prezentarea abundentei la nivel de populatie, pe clase de varsta care ilustreaza structura demografica instantanee. Clasele de varsta se prezinta in histograme, cu frecventa egala sau frecvente diferite. Modelele de reprezentare grafica pot fi extrem de diferite, parte din ele selectate direct de pe computer. Amplitudinea claselor de frecvente poate fi diferita (exemplu: prezentare insumata pentru toti indivizii masculi si femele din aceeasi clasa; sau pe sexe). Modelul histogramei poate diferi in functie de nivelul la care s-a facut operatiunea de sampling (supra- sau subestimata), iar alte tipuri se reprezinta sub forma de distributie cumulata (Fig. 5-5)

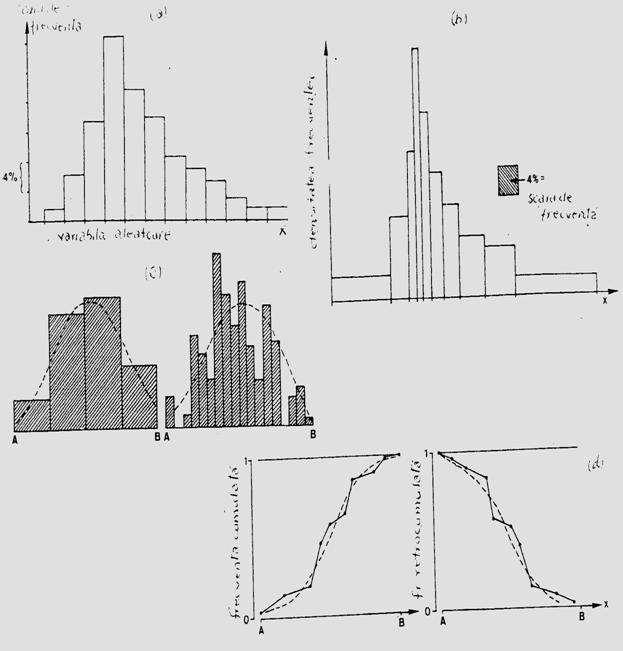
Fig. 5- Tipuri simplificate de histograme si curbe de reprezentare grafica utilizate in descrierea staticii populatiilor. (a). Histograma cu clase de frecventa egale ca amplitudine. (b). Clase cu frecventa egala. (c). Reprezentarea grafica a aceleiasi distributii prin histograme cu amplitudinea diferita a claselor. (d). Model de curba cunumar si frecventa cumulata (dupa Stan, 1990; Frontier si Pichod-Vial, 1998).

Descrierea cineticii unei populatii. Se refera la descrierea staticii populatiei cat si a dinamicii populatiei. Cinetica populatiei se traduce printr-o curba de variatie a abundentei in functie de timp. Confundam frecvent aceasta curba cu ceea ce ecologii denumesc curba de zbor (la pasari si insecte). Ea evidentiaza variatia abundentei in timp si spatiu dar nu precizeaza cauzele sau actiunile din exterior ori interior, care o determina.

In fizica, statica este studiul echilibrului corpurilor imobile; cinetica este studiul miscarii corpurilor; dinamica explica miscarile corpurilor prin actiunea unor "forte". Precizam ca aceasta diferentiere si terminologie nu este respectata intru'totul. Astfel, sunt articolele de ecologie unde se vorbeste de dinamica populatiei vegetale, planctonice sau de animale, dar de fapt este o variatie a abundentei in timp, ceea ce de fapt este cinetica populatiei respective. Daca ar fi dinamica reala (datorata unor forte atunci curba dinamicii ar trebui interpretata prin implicarea tuturor cauzelor posibile care determina variatia demografica: multiplicarea indivizilor, reproducerea sexuata sau asexuata, rata cresterii, mortalitatea, imigrarea, emigrarea etc). In aceste conditii a realiza o dinamica reala care sa explice dinamica abundentei, este necesara modelarea dinamicii (se alege un "compartiment" reprezentand biomasa unei regiuni delimitate a spatiului si se analizeaza fluxul de intrare - natalitate + imigrare, respectiv fluxul de iesire - mortalitate + emigrare; in acest fel se realizeaza variatia biomasei in timp; in acest fel vorbim de analiza dinamicii populatiei in sistem ecologic deschis si nu unul izolat).

3.2. Ciclul biologic (ciclul de viata). Longevitatea si curba de supravietuire

a. Ciclul de viata (ciclul biologic; tabelul de viata - life table). Este o reprezentare a structurii de varsta a populatiei, la nivel de individ, a succesiunii stadiilor si generatiilor, a evolutiei parametrilor calitativi si cantitativi, dependenti de crestere, dezvoltare si supravietuire.

In conditii naturale, practic este imposibila obtinerea unui model de "ciclu biologic populational" care sa caracterizeze o populatie. Chiar si in conditii de laborator, unde se pot prelucra datele la nivel populational, nu este vorba de o populatie ecologica ci de una elementara care pe deasupra poate fi "modelata" prin artefacte de selectie artificiala. Dar datele au valoare informationala.

La plante, ciclul biologic este alcatuit din faze specifice; samanta, plantula, individ tanar, planta (arbore) matur.

La animale exista stadii in functie de categoria sistematica:

- la unicelulare celula este un individ care trece prin faze de dezvoltare;

- la pluricelulare nevertebrate exista succesiune de stadii si faze (ou, juvenil, tineret, stadiu matur - adult); la insecte exista cele doua tipuri principale de metamorfoza: heterometabola (juvenilii se aseamana cu adultii) si holometabola (exista stadiile de ou, larva, pupa si adult); la vertebrate exista stadiile de ou, pui, tineret, adulti.

Tabelul 6-1

Ciclul de viata la Mamestra brassicae . Durata stadiilor si antibioza, in conditiile cresterii in laborator, pe diete artificiale a speciei mamestra brassicae (dupa Stan si colab., 1993)

Tabelul 6-1 continuare

- notare conventionala a diferitelor variante de dieta artificiala; ² - coeficient de variatie; ³ - durata stadiilor in zile ( eroarea standard; aceeasi litera indica diferente nesemnificative intre variante (D'sNMRT; P = 0,05); 4 - numarul adultilor care au iesit din pupe; ⁵ - numarul mediu de oua depuse/femela + numarul mediu de oua ramase in ovare, dupa moartea femelei; ⁶ - % de oua fertile din totalul de oua / femela; ⁷ - numarul de larve tinere iesite din ouale fecundate

In studiile care se fac la nivel populational, in conditii de laborator, se estimeaza valori medii pentru un numar mare de indivizi sau generatii succesive. Datele acestea servesc pentru obtinerea de informatii asupra populatiilor din natura. De asemenea, adulti capturati din camp, sunt studiati in custi speciale in conditii naturale, pe durata mai multor generatii, in conditii de variatie a factorilor ecologici. Si in acest caz datele obtinute nu ofera certitudinea exacta a ciclului biologic al unei populatii ecologice.

In conditii de laborator un tabel al ciclului de viata cuprinde particularitatile calitative si cantitative ale populatiei ca raspuns la factori de mediu. Reactia adversa de raspuns a organismelor la factorii ecologici sau de alta natura, poarta numele de antibioza (Tabelul 6).

b. Longevitatea (durata de viata). Se estimeaza ca valoare medie pentru toti indivizii din experiment. In conditii experimentale de laborator se lucreaza cu repetitii pentru asigurarea unui optim de informatie in calculele statistice. De obicei aceste date se confrunta cu cele din natura care, evident, sunt deosebit de dificil de apreciat. Durata de viata este in functie de o serie de factori ecologici, temperatura fiind unul fizic cu semnificatia ecologica cea mai mare (Fig. 5-6).

c. Curba de supravietuire. In sine supravietuirea semnifica numarul de indivizi ai unei populatii care sunt inca in viata la un moment dat. Evident, supravietuirea este asociata cu mortalitatea (cresterea mortalitatii determina diminuarea numarului de supravietuitori).

Indivizii care mor intr-o populatie descriu o curba cu trend descrescator (curba mortalitatii). Aceasta este corelata cu varsta si dependenta de specie sau alti factori de mediu (Fig. 5-7, a). Indivizii ramasi vii la fiecare moment in populatie definesc supravietuirea.

Curba supravietuirii are un trend opus curbei mortalitatii (Fig. 5-7, b).

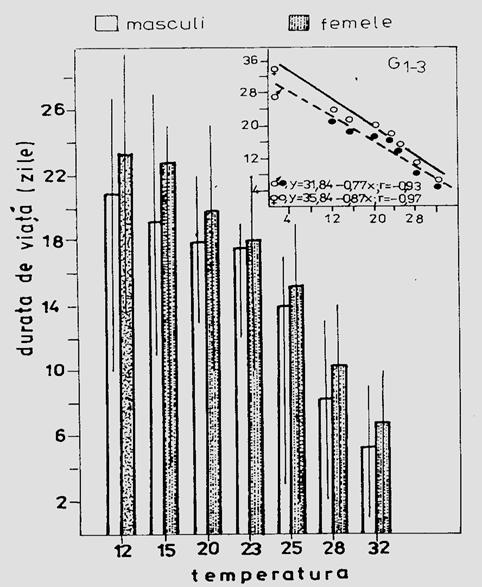
Fig. 5-6. Influenta temperaturii asupra duratei de viata a adultilor speciei Xestia c-nigrum. Estimare la nivel populational. Media a 3 generatii crescute in conditii controlate de laborator (dupa Stan, 1990).

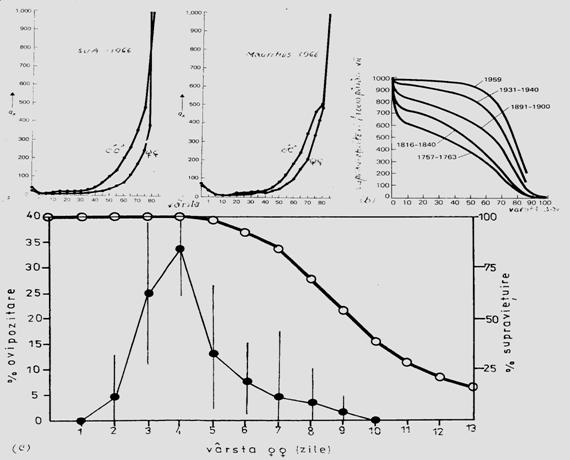
Fig. 5-7. (a). Un model de curba a mortalitasii (ex. mortalitatea populatiei din America, 1966, in functie de varsta (q_x = mortalitatea). (b) Model de curbe de supravietuire a caror trend ilustreaza rata de supravietuire a populatiei din Suedia, la diferite intervale de timp. (c). O alta reprezentare grafica ce ilustreaza supravietuirea indivizilor unei specii la nivelul unui experiment biologic sau ecologic in conditii experimentale de laborator (% supravietuire a femelelor de Mamestra brassicae care au ovipozitat, in functie de varsta acestora) (date din Smith, 1974; Stan, 1990).

Datele din cercetarile ecologice evidentiaza existenta a 3 tipuri esentiale de curbe de supravietuire (Fig.5-8)

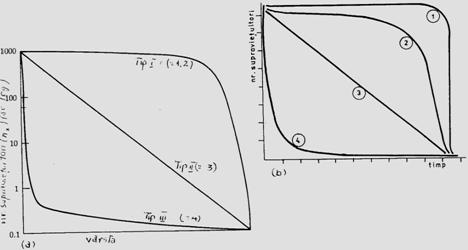
Fig. 5-8. (a). Modelul ipotetic al celor 3 forme de curbe de supravietuire in lumea vie (tipul I include: omul, mamifere, animale vertebrate mari; tipul II include: pasari, nevertebrate etc; tipul III include: insecte, organisme mici, juvenili, nevertebrate bentice, moluste, pesti etc). (b). Un model cu 4 tipuri (tipul I din graficul anterior a devenit tipul I; tipul 1 de aici este o varianta a tipului II, dar considerata de unii cercetatori ca reprezentativa, la specii de insecte cu viata scurta - de ex. efemeridele - la care se realizeaza mortalitatea in masa) (dupa Brewer, 1988; Stiling, 1996).

3.3. Generatia. Modelul de emergenta. Clasele de varsta. Rata sexelor

Alaturi de natalitate, mortalitate, longvitate, supravietuire, statica populatiei este caracterizata si de alti parametrii importanti, in functie de care se poate analiza, compara si clasifica. Acestia sunt: generatia, emergenta, clasele de varsta, rata sexelor.

a. Generatia. Generatia reprezinta o grupare de indivizi, urmasi apartinand unei femele sau unui cuplu, la randul lor apartinand unei populatii (specii), cu un ciclu biologic reprezentat de stadii morfologice si derulat pe intervalul nastere - moarte.

Evidentierea si evaluarea cantitativa a unei generatii este in functie de specie si este un parametru caracteristic animalelor. In conditii naturale este dificil de apreciat, dar se poate studia in conditii de laborator. Mai importante sunt urmatoarele tipuri:

- la specii de vertebrate generatia parcurge intervalul nastere sau eclozare din ou, trece prin stadiile de juvenil (pui) si adult;

- la specii de nevertebrate fenomenul este mai complicat. De exemplu, la insecte ciclul biologic al unui individ este marcat de existenta a doua tipuri de metamorfoza: heterometabola (juvenilii se asemana cu adultii) si holometabola (exista 4 stadii: ou, larva, pupa, adult). Mai exista si o serie de alte situatii intermediare;

- la alte specii exista si substadii (juvenilli I, juvenili II, subadulti etc).

Indiferent de varianta, dar dependent de specie, generatia se intinde pe o anumita durata de timp. La unele specii durata unei generatii este de 1 an, la altele de 2 sau mai multi ani, in timp ce la specii mai mici (frecvent la nevertebrate) sunt doua sau mai multe generatii pe an (ex. Mamestra brassicae - 2 generatii; Cameraria ohridella - 5, 6 generatii).

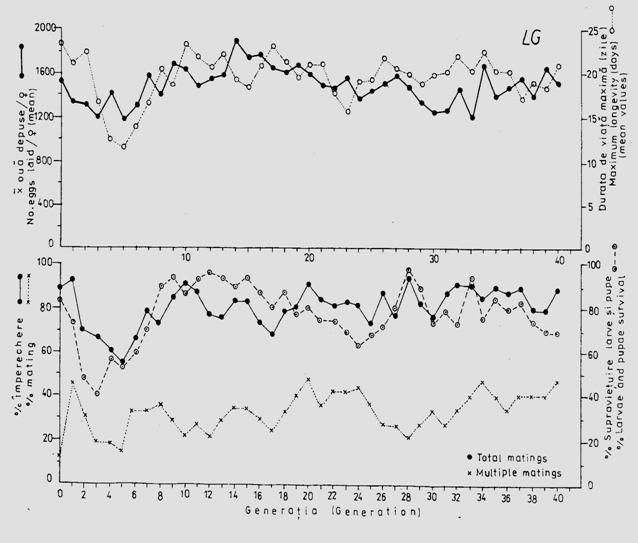
Fig. 5-9. Durata de viata la nivel de populatie, supravietuirea si potentialul reproductiv (imperechere, fecunditate) a unei linii de crestere (LG), la specia Mamestra brassicae, in conditiile cresterii speciei Mamestra brassicae in laborator pe diete artificiale, timp de 40 generatii succesive (dupa Stan si colab., 1998).

In laborator, in studii autecologice la specii de insecte, ca urmare a fenomenului de aclimatizare, in conditii speciale de manevrare a factorilor de mediu si prin procese de selectie artificiala, prin inlaturarea diapauzei, la Mamestra brassicae (2 generatii/an in natura) s-au obtinut 7-8 generatii/an (Stan si Chis, 1998).

Daca marimea populatiei unei insecte dintr-o anumita zona, este estimata la diferite intervale (ex. prin esantionare) se poate trasa o curba de variatie care sa vizualizeze modificarile numarului in timp. Marcam astfel dinamica (prezentata anterior) printr-o curba a populatiei. Pe aceste curbe se pot delimita: numarul de generatii, maximul dezvoltarii, numarul total al indivizilor, influenta diversilor factori asupra marimii populatiei, etc.

Daca se compara curbele dezvoltarii sezoniere pentru diferite specii de insecte, s-a constatat ca exista putine modele de baza ale schimbarilor temporale pe durata scurta. Aceste modele sunt dependente de biologia speciilor implicate.

In conditii controlate de laborator exista un ritm caracteristic al evolutiei populatiilor, rezultat al aclimatizarii si influentei selectiei artificiale. In timp, se inregistreaza o "stabilitate" a dezvoltarii, cu influente directe asupra potentialului reproductiv (Fig. 5-9) dar datele referitoare la durata generatiilor nu concorda cu cele din natura.

Specii cu o generatie/an. Unele specii au o singura generatie/an. Cresterea numerica a populatiilor acestora poate fi rezultatul numai al ovipozitari, insa modelul specific al cresterii numerice depinde de durata perioadei de ovipozitare raportata la durata ciclului de viata (Fig. 5-10, a).

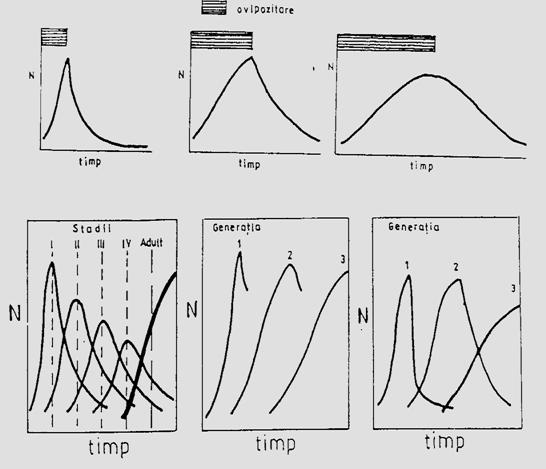
Fig. 5-10. (a). Influenta ovipozitarii asupra modelului de crestere a populatiei unei specii cu o singura generatie pe an, in functie de durata ovipozitarii. (b). Un model schematic al evolutiei dinamicii si marimii unei populatii in functie de numarul de generatii (dupa date din literatura; din Stan, 1994)

Se poate usor deduce ca o perioada scurta de ovipozitare determina preponderenta unui anumit stadiu de dezvoltare, intr-un anumit moment al dezvoltarii. Apoi, in fiecare stadiu de dezvoltare, modelul cresterii in timp tinde sa fie similar (in forma) cu cel al curbei pentru evolutia intergului organism. Crescand perioada de ovipozitare, timpul necesar intregului organism in a completa stadiile sale de dezvoltare creste, iar suprapunerea intre stadii se accentueaza (Fig. 5-10, b, A).

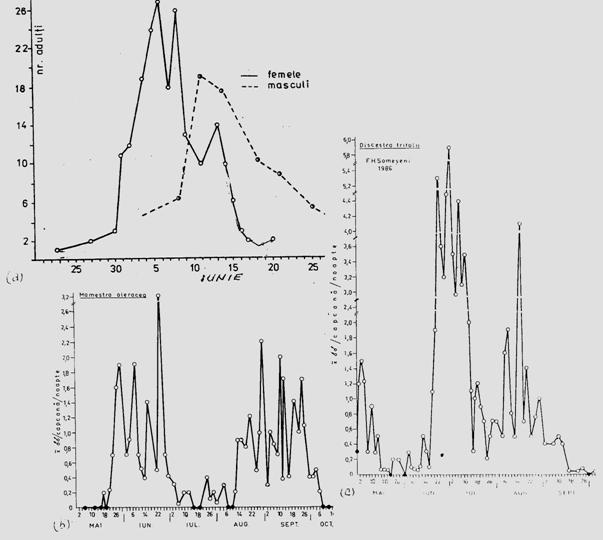
Fig. 5-11. Evidentierea numarului de generatii/an la insecte, prin vizualizarea variatiei abundentei cu ajutorul curbei de zbor (exemplu pentru speciile: Ostrinia nubilalis - cu 1 generatie (a), Lacanobia oleracea - cu 2 generatii (b), Discestra trifolii - cu 3 generatii (c) (dupa Stan, 1990; Crisan si Stan, 1996).

Specii cu 2-3 generatii/an. Generatiile succesive prezinta si ele diferite modele ale schimbarii numerice. O diapauza hibernala poate astfel determina o crestere rapida a ovipozitarii in G1, cu atingerea rapida a unui maxim, dupa care si scaderea este la fel de rapida iar curba prezinta un varf asimetric. Si pentru ca variatia normala in timp tinde sa completeze dezvoltarea in timpul primei generatii, perioada de ovipoziare din G2 va fi mai lunga. Deci, evolutia normala a timpului individual de dezvoltare, determina o lungire a perioadei de ovipozitare in generatii succesive (Fig. 5-10, b, B). Partea descendenta a curbei (declinul de dupa atingerea maximului) este asociata cu modelul specific al mortalitatii la nivelul populatiei. Fenomenul este evident la speciile cu perioada de ovipozitare scurta, dar cand o perioada de ovipozitare este lunga, raportat la timpul total necesar pentru completarea dezvoltarii, indivizii apartinand la diferite stadii de dezvoltare, sunt prezenti simultan in populatie, fenomenul de mortalitate fiind mai putin distinct (Fig. 5-10, b, C).

In cercetari ecologice la specii de insecte, numarul de generatii/an poate fi ilustrat in conditiile unui monitoring continuu, pe baza datelor de captura, ilustrand variatia abundentei cu ajutorul curbei de zbor (Fig. 5-11).

Specii de insecte cu mai mult de 3 generatii/an In conditii deosebit de favorabile pot exista mai mult de 3 generatii pe an. In aceasta situatie fenomenul ilustrat in Fig. 4-10, b, B este si mai accentuat. In aceasta situatie, indivizii apartinand mai multor generatii se pot reproduce in acelasi timp iar generatiile succesive nu se mai disting. Un asemenea caz este intalnit la specia Cameraria ohridella (Lepidoptera), care are 5-6 generatii/an

Modelele de ovipozitare (natalitatea), pe de o parte, si mortalitatea, pe de alta parte, in cadrul unei generatii, se pot amesteca cu cele ale altor generatii si ambele pot determina o 'rata medie'. O completa suprapunere a generatiilor va fi caracterizata de absenta unor modificari pe durata scurta de timp, la nivelul populatiilor.

b. Modelul de emergenta. Emergenta este fenomenul de iesire a adultului din invelisul pupal, la speciile de insecte, cu metamorfoza holometabola (uneori este confundata terminologic cu eclozarea care in realitate este iesirea larvei din ou). O semnificatie deosebita au aceste date din punct de vedere practic, in actiunile de control, management si combatere a insectelor daunatoare. Si in acest caz, pentru lamurirea multor aspecte, este necesara o comparare a datelor din camp cu cele obtinute in laborator. Se cunosc (novak 1974) 9 tipuri reprezentative ale modelului de emergenta. In conditiile cresterii speciei in laborator, acest model se poate modifica, mai mult sau mai putin. In functie de specie, exista mai multe tipuri de emergenta (Fig. 5-12).

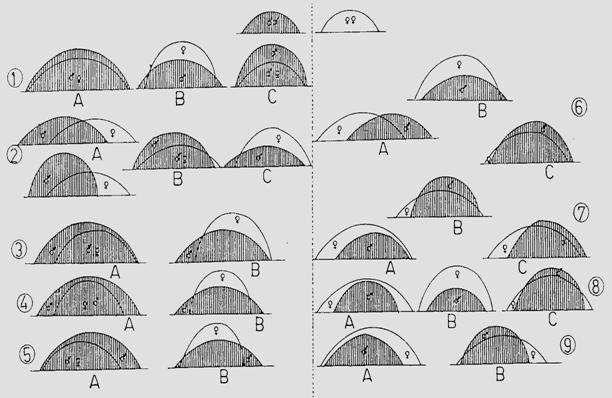
Fig. 5-12. Tipuri de emergenta la lepidoptere (Nicolescu si Stan, 1997; adaptat si completat dupa Novak, 1974).

Modelul de emergenta apare ca un caracter specific dar factorii ecologici sau factori tehnici dependentie de metodologia de cercetare, pot influenta acest model. Astfel. Specia Mamestra brassicae a fost incadrata (novak, 1974) in modelul VIII, ca specie protogina (Fig. 4-12).

Alte cercetari (sivcev, 1983; stan si colab., 1987), au sustinut aceste date, dar modelul tipic pentru populatiile din tara noastra este tipul IX, adica fenomenul protoginiei nu este intotdeauna marcant (stan si colab., 1994), inceputul zborului se poate suprapune la cele doua sexe, sau chiar sa emearga masculul cu 1-2 zile inainte. Lucrurile se complica putin si datorita nivelului redus al populatiilor in camp cat si generatia pentru care se studiaza. Mai mult, au fost diferente privind inceputul emergentei intre ecosisteme diferite (la capcanele din padure, masculii au initiat zborul inaintea zborului femelelor din camp de la capcana luminoasa).

Emergenta are semnificatie importanta in privinta corelatiilor dintre diferiti parametrii populationali si in contextul utilizarii capcanelor feromonale in controlul speciei, astfel ca protoginia (mai intai emerg femelele) devine concurenta pentru feromonul sexual sintetic.

In conditiile cresterii in laborator, modelul de emergenta se modifica intr-o oarecare masura (Tabelul 7), dar va domina tot tipul de emergenta IX. Corelarea datelor din camp si laborator, permit o apreciere cat mai corecta, calitativ-cantitativa, asupra populatiilor din camp.

Compararea datelor pentru diferite situatii cuprinse in tabelul de mai sus, evidentiaza urmatoarele aspecte:

- exista similaritate intre valorile RS pentru datele din camp la populatiile din Serbia si Transilvania; pentru datele din Boemia, valoarea RS indica dominanta neta a masculilor (sunt implicate aspecte legate de comportament (stan si colab.,1987; stan si colab

- datele personale arata, pentru emergenta, un ME care oscileaza in jurul lui 1, in schimb, pentru adultii capturati in capcana luminoasa se observa dominanta femelelor (datele sprijina ipoteza noastra privind comportamentul caracteristic de reproducere al acestei specii);

Tabelul 7

Evolutia ratei sexelor (RS) si a modelului de emergenta (ME) la Mamestra brassicae, in diferite generatii, crescute in conditii de laborator; (studii cu valori estimate la nivel populational: A -inceputul stadiului de adult, B - mijloc, C - sfarsit stadiului, D - intreg stadiul de adult)

^* - custi cu pupe in camp (larve recoltate din camp); ^** - date din laborator

- modelul de emergenta (ME) in camp este dominat de tipul IX-X care evidentiaza protoginia speciei, dar in unii ani, inceputul zborului nu este marcat distinct (asociat cu nivelul constant scazut al populatiilor si cu generatia);

- in conditii de laborator RS la pupe a fost similar cu RS la adultii emersi, iar ME a fost variabil (asociat printre altele si cu fenomenul de selectie artificiala a larvelor in procesul de crestere), dar cel mai frecvent s-a intilnit tot tipul IX.

c. Structura pe varste (piramida varstelor, clasele de varsta) Cercetarile cologice trebuie sa tina cont in mod obligatoriu de faptul ca efectivul unei populatii este alcatuit din indivizi care biologic sunt inegali intre ei, in primul rand prin varsta. In functie de scopul cercetarilor este necesar sa fie cunoscuta ponderea fiecarei varste in populatie pentru ca aceasta sa fie corect evaluata.

In raport cu reproducerea se disting 3 varste ecologice: prereproductiva (perioada de dezvoltare si maturizare), a reproducerii si postreproductiva. Cele 3 varste ecologice corespund la 3 clase de varsta: juvenili, adulti si batrani. La unele specii, juvenilii sunt incadrati in dua grupe: juvenili I, juvenili II (Fig. 5-13, a). Pentru specii de insecte holometabole unde exista cele 4 stadii (ou, larva, pupa, adult), stadiul de larva este caracterizat de 5-7 varste (Fig. 5-13, b).

Modul de distributie al varstei la nivelul populatiei reflevta vitalitatea si capacitatea sa de crestere numerica. Daca se reprezinta grafic ponderea fiecarei clase de varsta in populatie, aceasta caracterizeaza structura de varsta a populatiei. In functie de ponderea fiecarei clase in cadrul reprezentarii se poate aprecia starea si tendinta evolutiova a populatiei la un moment dat. Ponderea juvenililor intr-o populatie la un moment dat caracterizeaza o tendinta de crestere numerica. Dimpotriva, o pondere mai mare a adultilor batrani caracterizeaza un declin numeric. Cand ponderea celor 3 clase este aproximativ egala, populatia este stationara.

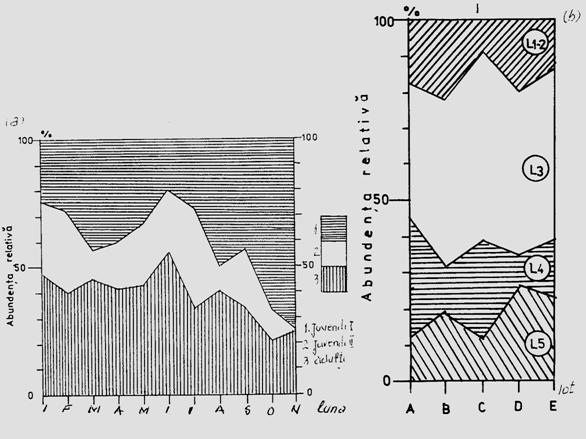
Fig. 5-13. Reprezentarea structurii populatiei in functie de varsta. (a). abundenta relativa a populatiilor de colembole din solul unei paduri de foioase, pe durata unui an. (b). abundenta relativa, la nivel de virsta larvara, pentru o populatie de Mamestra brassicae, in 5 tipuri de loturi experimentale cultivate cu specii de crucifere (dupa Stan, 1994).

Frecvent se intalneste si terminologia de piramida a varstelor care sta la baza intocmirii graficelor care ilustreaza supravietuirea .

Studiul curbelor de supravietuire prezinta un grad mare de interes pentru ecologisti. Sew poate surprinde si preciza varsta optima pentru o anumita activitate comportamentala dar si perioada ineficienta sau mai vulnerabila. In felul acesta se poate prevedea evolutia ulterioara a populatiei si valorile numerice pe care le poate atinge in descendenta.

Orice populatie, de-a lungul unei generatii este marcata si de diversitate interioara. Sub aspect genetic populatia poate fi caraterizata de polimorfism genetic. Sub aspect ecologic este caracterizata de existenta micropopulatiilor. Acest fenomen este deosebit de important de cunoscut in studiul populatiilor in natura, deoarece este posibil ca o micropopulatie sa fie considerata o populatie distincta, mai ales daca ea este delimitata spatial (ex. intr-un camp de cultura exista cel putin 2 micropopulatii: una in mijlocul culturii si alta la marginea culturii). In exemplul sugerat mai sus, cunoasterea modelului comportamental al speciei este de asemenea foarte important deoarece este posibil ca micropopulatia sa fie o agregare temporara asociata cu un anume model comportamental.

Intr-o generatie a oricarei populatii (specii), indivizii se deosebesc prin varsta. Aceasta este structura de varsta a populatiei si se refera la proportia de indivizi de varste diferite. Cei de aceeasi varsta constituie o clasa de varsta. Numarul claselor de varsta redau structura de varsta a populatiei care reprezentata grafic poate fi redata printr-un model geometric - piramida claselor de varsta (Fig. 5-14).

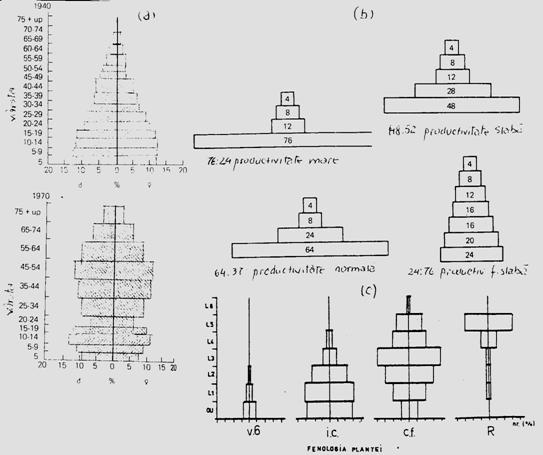
Fig. 5-14. Ilustrarea unor modele de piramide a claselor de varsta. (1). Structura de varsta a populatiei dintr-o zona miniera, in anul 1940 (a) si in anul 1970 (b) (dupa Smith, 1974). (2). Modele teoretice de piramide a claselor de varsta: o populatie in care predomina indivizii tineri (a), o populatie echilibrata (normala) (b), o populatie slab productiva (c) si o populatie cu un numar foarte mic de indivizi tineri (foarte slab productiva) (d). (dupa Alexander, 1958). (3). Structura pe varste a populatiei de Mamestra brassicae (larva) in relatie directa cu fenologia plantei de cultura (varza)(v.6 = verticil de 6 frunze; i.c. = inceput de formare a capatanii; c.f = capatana formata; R - la recoltare) (dupa Stan, 1994)

Varsta poate fi exprimata ca unitate de timp (ore, zile, luni, ani) sau ca secvente functionale (prereproductiv, reproductiv, postreproductiv). Pentru multe specii de animale varsta individului este importanta pentru specificarea rolului sau in populatie si in acest fel pot fi evaluati o serie de parametri ce pot defini rata reproductiva, tipurile de relatii comportamentale si caracteristicile functionale. O populatie in crestere sau in declin prezinta si variatii la nivelul structurii de varsta. Daca de ex. rata de crestere este 0 iar populatia nu se schimba in marime, distributia stabila a varstei poarta denumirea de distributie stationara a varstei. Intro populatie care creste si una care este stabila structura de varsta este caracteristica (Fig. 5-15).

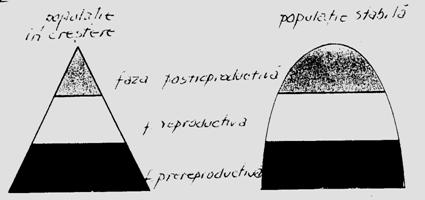
Fig. 5-1 Reprezentarea schematica a structurii de varsta la o populatie care creste si una stabila (dupa Brewer, 1988).

Structura de varsta la plante. Anterior am aratat ca varsta unui individ indica rolul sau in populatie. Dar acest lucru este valabil si in cazul plantelor. Ca si in cazul animalelor si la plante ciclul de viata poate fi urmarit de la samanta pana la moartea plantei, ilustrand acest aspect prin modalitati studiate la animale. La alte specii de plante (cat si animale poikiloterme) acestu lucru este mai dificil de urmarit si ilustrat. Unele seminte pot avea varsta de 25-30 ani si au putere germinativa. Dupa germinare se dezvolta normal. In acest caz daca punem varsta 0 in momentul germinarii, ar trebui sa marcam momentul mortii cand se formeaza samanta sau cand incepe germinatia ?.

La alte specii de plante structura de varsta nu prezinta interes sau prezinta totusi dar mai putin decat in cazul animalelor. In aceste situatii, pentru calcule sau reprezentari grafice, este mai importanta marimea stadiului decat varsta.

Rata sexelor (sex-ratio Este o alta caracteristica importanta in evolutia popultiilor. Rata sexelor este raportul dintre masculi si femele la nivelul unei populatii. Cercetarile ecologice prezinta acest raport cu oscilatii in jurul valorii 1, in functie de specie.

Se pot constata in literatura de specialitate, variatii ale valoriilor, pentru aceeasi specie, in timp si spatiu, in functie de variatia unor factori interni si externi in natura, iar in laborator, dependent si de metodologia de conducere a experimentelor. Paralel cu modificarea valorii pentru rata sexelor, se modifica si indicele sexual. Variabilitatea in captura, pentru o perioada mai lunga de timp, intr-o aceeasi zona, este asociata cu biologia speciei, comportamentul, actiunea factorilor de mediu si relatiile interspecifice, fiind oglindita prin valorile coeficientului de variatie (Tabelul 8). Chiar si prin aceeasi metoda de captura difera reactia de raspuns la calitatea stimulului atractant.

Caracterizarea ecologica a populatiilor unei specii are importanta nu numai din punct de vedere teoretic pentru conoasterea particularitatilor speciei la nivel de populatii geoagrafice sau ecologice, dar si din punct de vedere practic, pentru managementul speciilor daunatoare.

Pe de alta parte, in conditiile cresterii speciei in laborator, se poate moidifica rata sexelor, fata de situatia din camp. In conditiile in care cresterea este condusa pentru o generatie completa (fara artefacte de selectie a materialului biologic), datele obtinute furnizeaza o informatie corecta asupra ratei sexelor.

Tabelul 8

Date sintetice, reprezentand valorile ratei sexelor (RS=nr.♂♂/nr.♀♀), indicelui sexual (IS=nr. ♀♀/ (nr. ♂♂+ nr. ♀♀) si coeficientului de variabilitate (Cv=s/x), la cateva specii de lepidoptere noctuide, dupa diferiti autori, pe baza cercetarilor cu capcane luminoase in camp.

^* cercetari facute in perioada 1967-1971;

^** cercetari in zona Cluj Romania; 1983-1990; estimari medii);

^***cercetari facute in perioada 1967-1979.

3.4. Spatiul populatiei. Principiul lui Allee. Intercompensatia. Teritorialitatea. Dispersia, migrarea, deplasarile locale

Spatiul populatiei. Organismele vii, plante si animale, la fel ca oamenii, frecvent manifesta un comportament caracteristic de agregare, mutual benefic, la fel cum, frecvent, indivizii se disperseaza, pentru "avantaje" individuale. Ambele strategii pot avea valoare de supravietuire (valoare adaptativa), dependent de specie si de circumstantele de moment. Unele specii alterneaza cele doua strategii, in functie de sezon (se agrega iarna, se disperseaza vara). Multe specii de plante si animale (ex. cele sesile sau fixate permanent) formeaza colonii dense, in timp ce alte specii de plante (ex. specii de desert) dispun de modalitati chimice (ex. repelenti, deterenti, toxine) pentru a evita supraaglomerarea, competitia sau concurenta. Pentru animalele mobile, lucrurile sunt mai simple, ele dispunand de capacitatea mobilitatii in cadrul unui model comportamental care defineste teritorialitatea (ex. cazul pasarilor cantatoare) (Odum, 1993).

Teritorialitatea. Reprezinta ocuparea unei suprafete de catre indivizii unei populatii sau de o populatie intreaga, rezultat a unei ierarhizari biologice si a unui model comportamental. Cele mai caracteristice sunt comportamentul social (albine, furnici, bondari, viespi etc) si comportamentul de agregare (insecte - ex. Scolitidae, lilieci). Ar mai exista si un comportament de dominanta, rezultat al ierarhizarii unor functii in colectivitatea unei populatii. Exista insa o serie de puncte de vedere care au concluzionat ca despre teritorialitate se poate vorbi doar in cazul comportamentului social (Fratwell si Lucas, 1969).

Comportamentul teritorial este mai pronuntat la vertebrate si mai rar la nevertebrate, unde se mai manifesta un comprtament parental de ingrijire a pontei sau a urmasilor (ex. la specii de artropode - crustacee sau insecte). La pasari, dupa cum am precizat mai sus, este un model comportamental asociat cu reproducerea, locuirea cuibului sau neinterferenta cu alti indivizi conspecifici. Exista 3 puncte de vedere:

a. teritorialitatea functioneaza ca un factor dependent de densitate (in conditii de supraaglomerare, deci de densitate mare, unii masculi se deplaseaza in alte habitate, aici populatia avand densitate mica sunt selectate habitatele optime, iar populatia se reface usor) ( Kluijver si Tinbergen, 1953);

b. teritorialitatea este considerata ca o suprafata care se poate comprima pana la o anumita dimensiune. Marimea teritoriului descreste cu cat densitatea creste; astfel teritoriul este "comprimat" si nu mai poate intra nimeni in el; se declanseaza comportamentul agresiv, iar indivizii mai putini agresivi parasesc teritoriul. Si la pasari teritorialitatea functioneaza ca un factor dependent de densitate si determina manifestarea comportamentului teritorial (Brown, 1969);

c. teritorialitatea actioneaza numai in afara spatiului individului in habitat iar densitatea este determinata independent de comportament (la o anumita densitate, indivizii se separa cat de mult este posibil si nu se stabilesc ranguri sau trepte de ierarhie intre ei) (Lack, 1964).

Intercompensatia. Este un fenomen caracteristic populatiilor, avand ca principiu interactiunea dintre natura factorilor si marimea populatiei (Errington, 1967). O serie de calamitati pot afecta sau chiar distruge populatiile locale. In general insa este vorba despre o reducere a numarului, fenomen care se manifesta doar temporar. Indivizii supravietuitori, avand la dispozitie un habitat favorabil pot reface populatia deoarece fiind putini competitia pentru hrana este foarte redusa si astfel se pot inmulti.

Supraaglomerare, agregarea excesiva, nu este favorabila populatiei deoarece amplifica lupta pentru existenta, iar luptele dintre indivizi vor defavoriza specie. Pe de alta parte, rezultatul acestor conflicte este aparitia de boli sau chiar epidemii ce pot avea uneori efecte catastrofale asupra populatiei sau chiar a speciei.

Subaglomerarea este in avantajul populatiei daca facem referire la boli sau epidemii. Dar, ecologic, subaglomerarea este si ea dezavantajoasa pentru specie. Un numar prea mic de indivzi nu vor putea valorifica rentabil resursele mediului, iar atunci cand o alta parte va fi eliminata, nu se mai poate reface populatia.

Din cele afirmate rezulta ca ambele strategii sunt defavorabile populatiei, supravietuirii indivizilor.

Principiul lui Allee (Allee, 1958). Daca si subaglomerarea este dezavantajoasa, la fel ca si supraaglomerarea, autorul sugereaza ca trebuie sa existe o densitate medie optima in care populatia sa ocupe o stare intermediara intre cele doua forme, totusi mai mare decat una minimala (un individ sau o pereche) fenomen denumit principiul lui Allee sau efectul Allee. Principiul poate fi inteles in conexiune cu rata cresterii populatiei .

Ca principiu, amintim aici cateva aspecte pentru a ilustra principiul lui Allee. Daca populatia creste dupa o curba strict logistica va exista o linie dreapta care marcheaza rata cresterii / individ, linie care are un trend oblic-jos, dependent de cresterea densitatii (Fig. 5-16, a).

Principiul lui Allee actioneaza tocmai la nivelul spre minim al densitatii populatiei, ca o curba (linia intrerupta) care va modifica trendul initial. In felul acesta se evidentiaza existenta unor valori limita (densitate minima si densitate maxima); intre aceste valori populatia se mentine iar dincolo de aceste valori ea este eliminata. Intre cele doua extreme exista un optim ce va asigura un maxim de indivizi (supravietuitori) care vor reface populatia la un nivel favorabil, in generatia urmatoare. Stugren (1975) ilustreaza acest aspect cu doua exemple date de Elton (1927) (pe o insula din Oc. Atlantic s-au introdus cateva pisici pentru a starpi sobolanii de aici; fiind prea putine, sub limita inferioara a supravietuirii, sobolanii au fost cei care au omorat pisicile. Un alt exemplu: tot pe o insula s-au introdus pisici pentru a starpi iepurele de vizuina; pisicile au inlaturat toti iepurii dar apoi au pierit si ele deoarece nu mai aveau o alta baza trofica; de data aceasta numarul pisicilor a fost prea mare, deasupra limitei superioare de supravietuire)

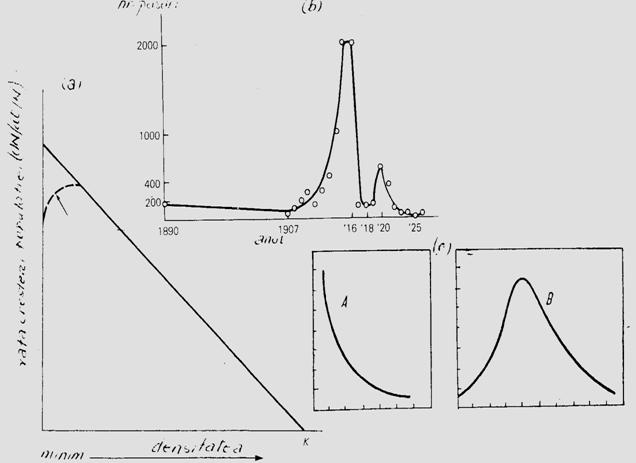
Fig. 5-16. (a). Ilustrare grafica sugestiva a relatiei dintre densitatea populatiei si rata cresterii populatiei (numarul de supravietuitori), in conditiile existentei unei cresteri dupa o curba logistica, si locul de manifestare a efectului Allee (dupa Brewer, 1988). (b). Principiul lui Allee ilustrat separat: 1 - curba logistica teoretica; 2 - curba normala cu minim, maxim si interval optim (dupa Stugren, 1975); 3 - exemplul dat de Allee si colab. (1949) cu specia Tympanuchus cupido (din Brewer, 1988).

Conform efectului Allee relatia dintre densitate si rata cresterii (procentajul de supravietuitori) nu se exprima dupa o curba conrtinuu descrescatoare ci dupa una de tip clopot (Fig. 5-16, b, 1, 2) ilustrata cu un exemplu al unei specii de pasare de prerie (Tympanuchus cupido) care marcheaza evolutia densitatii pe intervalul 1890-1925 (ultimul an marcand extinctia speciei) (Fig. 5-16, b, 3).

Exmplele date, dar mai ales realitatea ecologica arata ca o populatie nu poate creste la nesfarsit. Ea poate atinge un punct de echilibru dar permanent va fluctua in jurul acestuia. Acest punct de echilibru este o constanta pe termen lung in care densitatea medie a populatiei se apropie de "pretentiile" environmentului. Este de fapt un "punct culminant" de la care populatia tinde sa se intoarca la "dezordine". Punctul acesta de echilibru poate fi definit ca o densitate in care rata de crestere este 0 (r = 0), dar este mai degraba un indice statistic decat unul biologic. Exemplele unor studii ecologice arata ca populatiile fluctueaza intre valorile minime si maxime si ca aceste limite asigura stabilitatea populatiei. Cunoasterea naturii proceselor care regleaza numarul de plante si animale intr-o unitate environmentala sunt de fapt aspectele cele mai interesante din domeniul studiului ecologiei populatiilor.

Densitatea populatiei este determinata de variatia numarului de indivizi (organisme) subinfluenta unor factori externi sau interni. Exista doua categorii: factori independenti de densitate si factori dependenti de densitate.

Factori independenti de densitate.Acesti factori nu pot regla marimea populatiei deoarece reglarea implica un feedback homeostatic asociat cu densitatea. Factorii independenti de densitate pot insa actiona asupra cresterii sau descresterii populatiei. Se manifesta atunci cand nu actioneaza factori de dependenti de densitate sau se asociaza cu alte influente care induc schimbari in populatie. Au fost studiati mai mult la insecte. Cei mai importanti factori din aceasta categorie sunt: tipul de planta gazda si virsta, competitia cu alte specii, efectul generatiei anterioare asupra calitatii plantei gazda, numarul si tipul pradatorilor si parazitilor, temperatura etc (Sluss, 1967).

Factori dependenti de densitate. Aici reglarea marimii populatiei se realizeaza prin mecanisme homeostatice pe baza de feedback. Daca populatia creste prea mult, procese dpendente de densitate tind sa o scada. Si invers. Uneori rata de crestere a populatiei este invers corelata cu densitatea (cand densitatea creste, creste mortalitatea si scade natalitatea, rata de crestere devine negativa (r <0) si populatia intra in declin; cand densitatea descreste, se reduce mortalitatea, creste natalitatea si r > 0; cand r = 0 populatia nu se modifica sub raportul densitatii).

Cei mai importanti factori dependenti de densitate sunt: spatiul vital, hrana, comportamentul, calitatea genetica, migrarea, stresul.

Dispersia, migrarea, deplasarile locale. Sunt mecanisme comportamentale care actioneaza direct asupra efectivului si densitatii populatiei.

Dispersia (imprastierea, raspandirea) este in sine un mecanism care influenteaza densitatea populatiilor. In literatura engleza se mai folesesc doi termeni: [insect dispersal] (imprastierea, raspandirea insectelor) si [insect dispersion] (un model de distributie al indivizilor unei populatii in spatiul de existenta). Noi ii consideram insa sinonimi.

Dintre toate grupele de animale, insectele prezinta interesul cel mai mare pentru cercetatori, atat prin numarul net semnificativ mai mare al speciilor, cat si prin rol si importanta in ecosisteme. O serie de metode si tehnici pe care la vom aborda in continuare sunt caracteristice grupului dar tot atat de bine ele pot fi adaptate si pentru alte grupe de animale, tinand cont evident de modelul comportamental specific. Din aceste motive exemplificarile din acest capitol vor fi date din domeniul insectelor.

Probematica raspandirii si aprecierii marimii populatiilor de insecte in natura sunt preocupari de baza ale entomologilor, pe linia cercetarilor ecologice si comportamentale din ultima vreme, avand semnificatie atat din punct de vedere fundamental cat si aplicativ, mai ales in cadrul programelor de monitoring si combatere, la nivelul insectelor importante din punct de vedere economic. Tratate separat din punct de vedere didactic, o serie de notiuni ca: dinamica populatiilor, variabilitatea populationala, deplasarea si miscarea in camp (distributia, imprastierea, agregarea), teritorialitatea, colonizarea, stabilitatea, supravietuirea, rata natalitatii si mortalitatii, densitatea si reglarea nivelului populatiilor, supravietuirea, migrarea (emigrare, imigrare) sunt practic inseparabile pentru o interpretare unitara si complexa a populatiilor de animale..

La nivelul populatiilor de insecte (si nu numai), obtinerea de rezultate importante cu referire la aspectele demografice, genetice sau legate de protectie si conservare, sunt efectiv limitate de disponibilitatea informatiilor privind modelele de miscare care joaca un rol esential in determinarea ratei de extinctie locala si de estimare a marimii efective a populatiei (aut. cit. in Porter si Dooley, 1993). Indivizii se depaseaza din multe motive (hrana, reproducere, evitarea dusmanilor, conditii mai prielnice de viata), toate aceste deplasari influentand supravietuirea si rata de reproducere.

Pe linia intelegerii unor aspecte ecologice, cum sunt reglarea populatiilor, persistenta si evolutia (ca baza genetica a populatiilor), este esential de a cunoaste: tipul de indivizi care se deplaseaza si se disperseaza si compozitia cat mai precisa a populatiei respective (Lawrence, 1988). Pe de alta parte, pentru studiul miscarii in camp, daca se foloseste de exemplu metoda lansarii si recapurarii, se considera ca nu este suficient a efectua o operatiune de lansare si apoi a urmari activitatea in timp, deoarece orice model de distributie poate fi rezultattul insumarii a unui numar variabil de modele de miscare si care asigura distributii spatiale diverse, in circumstante diverse (Jones, 1977).

In caz de supraaglomerare, asociat cu cresterea comportamentului agresiv se produce dispersia indivizilor populatiei. Ierarhizarea sociala si teritorialitatea, intervin pe de alta parte si determina o parte a indivizilor sa se deplaseze in alte habitate ale arealului. Aici insa este posibil sa existe specii cohabitante sau competitive. Dispersia nu este ansa un fenomen asociat numai cu supraaglomerarea. Ea poate avea loc si la o densitate mica a populatiei (vezi in cap. 3 - dispersia organismelor sub influenta feromonilor epideictici) dar evident ca este mai pronuntata la densitati mari. Daca teritoriul este parasit si indivizii nu se mai intorc, are loc o emigrare (ea este asociata cu venirea in populatie a altor indivizi din exterior = imigrare). Emigrantii dintr-o suprafata de areal sunt imigranti in alta !.

Modelele de miscare pot fi diferite: miscare in interiorul unei suprafete de raspandire, langa baza de dezvoltare (imprastiere, folosita la noi si cu sensul de dispersie) sau miscari ample, mai degraba cu valoare adaptativa decat accidentale (migratii).

In determinarea structurii reale si durata de mentinere in timp a populatiei, una dintre problemele cele mai dificile pentru ecologi este masurarea ratei imigratie/emigratie (Dempster si colab., 1986). Sa mai amintim doar cu caracter informativ ca problematica migrarii insectelor este departe de a fi elucidata, atat ca mecanism in sine dar si ca modalitate directa de influentare a marimii populatiei (din care indivizii pleaca sau in care ajung) si aceasta pentru ca migratia nu este doar un simplu fenomen care ajuta insecta sa evite, temporar, unele conditii de viata neprielnice, ci este un mecanism fixat prin selectie naturala in conditii ecologice particulare (Novak & Spitzer, 1972; Lingren si colab., 1979).

Este interesant ca unii autori vorbesc de un interval larg de dispersie (aici cu sensul de distanta de raspandire). Cercetari facute (prin metoda de marcare-recaptura) in cadrul speciei Callosomia promethea (Lepidoptera: Saturniidae) au evidentiat pentru masculi distante de 14 km si 36,5 km, in 3 zile (Toliver si Jeffords, 1981) dar la Trichoplusia ni distanta maxima a fost de 196 km, pe un interval de 7 ore si o viteza medie de 4,9 km/ora (Kishaba si colab., 1967). Masculii de Spodoptera litura zboara in medie distante de 4-6 km pe noapte, distanta maxima fiind de 10-19 km pe noapte, femelele virgine dovedindu-se a avea un potential de zbor mai redus decat al masculior (Wakamura si colab., 1990). La insecte, mai ales la cele bune zburatoare, s-a constatat ca problematica se complica astunci cand sunt implicate fenomenele de dispersie si migrare in aer. Prin metode speciale de captura, inaltimea de zbor la unele noctuide a variat intre 61-1524 m si se pare ca aceasta nu este o constanta specifica.

Unele studii moderne cu capcane cu feromoni sexuali au putut evidentia faptul ca se poate stabili o relatie intre numarul de capturi si nivelul populatiei, ilustrata printr-o interpretare matematica a datelor (du Merle, 1985). Datorita comportamentului, lucrurile se complica intervenind relatiile complexe si competitia dintre feromonul sintetic si cel natural. Abateri pot sa apara si in conditiile folosire incorecte a altor modalitati de captura. Indifernt care ar fi metoda de captura se afirma totusi ca este dificil de a corela numarul de adulti capturati in capcane, cu numarul adultilor din camp, cu numarul de larve din generatia urmatoare sau cu daunele posibile (Minks, 1976).

In studiile ecologice ale populatiilor de animale, trei concepte domina azi orientarea cercetarilor: dependenta de densitate, reglarea marimii populatiilor si variabilitatea marimii populatiei.

Daca populatia de pe un anumit teritoriu este stabila (a atins sau este aproape de capacitatea portanta = capacitate de suportare = capacitate de sustinere (carrying capacity; vezi detalii in cap. 4.3.6.), miscarile de dispersie au o slaba influenta asupra densit[tii populatiei (eventual doar o usoara modelare a structurii de varsta). Dar miscarile de emigrare, induse de suprapopulare (aglomerare) si hrana putina reduc densitatea populatiei, influenteaza negativ structura de varsta si rata reproductiva a populatiei ramase in teritoriul respectiv. Orice imigrare duce la cresterea densitatii prin rata de crestere (implicit prin rata natalitatii). "Jocul" emigrare - imigrare este implicat in managementul mediului.

Vorbind despre dispersie, se iau in considerare doua modalitati: deplasari in intertiorul habitatului (nemigratoare) si deplasari intre habitate (dispersie prin migratie). Miscarile din interiorul habitatului au o evidenta valoare adaptativa, asigurand indivizilor necesarul in hrana, imperechere, suportul pentru ovipozitare, adapost. Am aratat la inceput ca si deplasarile de migratie au valoare adaptativa. Frecvent se vorbeste despre diferite tipuri de migrare: locala, sezoniera, anuala. Astfel, exista o strategie a migratiei, asociata cu dinamica populationala si cu densitatea acesteia (Solbreck, 1986). Pe de alta parte, aceasta este asociata cu diapauza. Mediatorii chimici si in special feromonii sexuali au permis obtinerea unor date semnificative in studiul migratiei si dispersiei, mai ales la poipulatii de lepidoptere (Witzgall si Priesner, 1985). Se vorbeste tot mai mult despre un comportament de dispersie, asociat cu receptivitatea sau nereceptivitatea indivizilor la actiunea stimulilor chimici (Carde si Elkinton, 1984). Fata de mediatorii chimici, comportamentul de raspuns difera in functie de sex, drept care nu se poate face intotdeauna o corecta estimare a densitatii numai pe aceasta cale.

Desi exista numeroase cercetari referitoare la deplasare, domina cele efectuate la insecte, acestea constituind si categoria sistematica unde studiile ecologice sunt cele mai dificile (Johnson, 1969; Taylor, 1986; Lawrence, 1988). Astfel, la insecte, de cele mai multe ori nu se cunoaste precis populatia de origine, de la care pornesc indivizii. La toate acestea se mai adauga si alte dificultati asociate cu marcarea cat si abilitatea cercetatorului in a masura cat mai precis distantele. Exista apoi diferente semnificative intre datele obtinute pe diferite grupe de insecte, din acest punct de vedere cele mai multe studii fiind facute la lepidoptere.

Exista mai multe modalitati pentru studiul comportamentului de dispersie, dar cea mai eficienta este metoda de capturare-marcare-lansare-recapturare sau pe scurt metoda de lansare-recaptura. Metoda este foarte buna atat pentru cercetari privind determinarea nivelului populatiilor dar si pentru studiul comportamentului de dispersie. S-a constatat ca unele insecte foarte bune zburatoare (ex. specii de fluturi) se deplaseaza la distante de peste 120 km (Lingren, 1979). Pentru asemenea studii se preteaza si populatiile provenite din cresteri in laborator. Se estimeaza urmatorii parametrii.

a. Rata de dispersie si detectarea heterogenitatii Se determina indepartarea (R) fata de punctul de lansare, intr-o anumita zi:

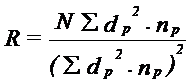
(N = nr. total de indivizi capturati in toate capcanele; d_p = distanta la care se recaptureaza fata de punctul p de lansare; n_p = nr. total de adulti prinsi in capcane, in punctul de recaptura, pentru aceleeasi distante fata de punctul p. La o curba normala, R = 3. Valori mai mari sau mai mici decat 3 indica heterogenitatea dispersiei (R>3 - curba intinsa; R<3 - curba abrupta).

b. Rata de dispersie ca distanta Se bazeaza pe determinarea vitezei de dispersie prin compararea variantelor (s²) pentru diferite zile de experimentare:

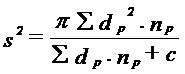
(n_p = media nr. indivizi gasiti in capcanele puse la o anumita distanta fata de punct; c = numarul de indivizi gasiti in centrul capcanei; π = 3,14).

Relatiile de mai sus s-au elaborat pe baza unor studii la Drosophila. Alte cercetari (la lacuste) au dovedit ca rata de dispersie a variat cu timpul de lansare, astfel ca pentru fiecare zi dupa lansare s-a calculat media radacinii patrate a distantei parcurse (D):

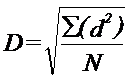
(d = distanta punctului de recapturare, fata de punctul de lansare; N = nr. total de indivizi capturati)

c. Metoda ecuatiei de regresie a relatiei dintre densitatea populatiei (y) si distanta fata de punctul de lansare (x). Iata cateva ecuatii pentru diferite studii:

y = a + b log x

y = a + b log x + c/x

log y = log a + bx

log y = log a + b log x

y = a + c/x

d. Elaborarea unei metode de cartare a punctelor de lansare si recapturare Se poate face cu ajutorul unei grile, in plan orizontal si vertical, prin estimarea mediei (x) si variantei (s²), in fiecare zi pentru fiecare grila. Daca mediile difera semnificativ, inseamna ca au existat dispersii marcante pentru o anume directie. Daca mediile sunt similare dar difera variantele,miscarile au fost nerandomizate, existand chiar metode pentru a descrie tipul de distributie spatiala (detalii in Southwood, 1966).

e. Evaluarea numarului de indivizi marcati care au parasit o anumita suprafata sau zona Numarul indivizilor care emigreaza sau imigreaza din populatie poate fi estimat prin marcare-recaptura. Daca nu exista natalitate si mortalitate, atunci pierderile si rata de diluare pot fi echivalente cu rata de migrare. Indicele L i n c o l n simplu poate fi folosit pentru a calcula proportia populatiei care a migrat, daca totalul populatiei este cunoscut (si nu exista natalitate si mortalitate).

f. Estimarea ratei populatiei care se deplaseaza intre doua zone (rata de emigrare) Se porneste de la presupunerea ca in doua populatii de insecte ratele de supravietuire sunt egale. Se fac 3 observatii: ziua 1 (t₁), ziua 2 (t₂) si ziua 3 (t₃) cu ajutorul metodei lui B a i l e y de tripla recaptura. In ziua 1, se marcheaza si se lanseaza, in ambele suprafete unde sunt cele doua populatii, un numar de indivizi (a₁). In ziua 2, se ia o proba (n₂) si se numara indivizii marcati si lansati (a₂). In ziua 3, se iau probe din ambele suprafete si se inregistreaza numarul tuturor indivizilor marcati. Datele se introduc apoi intr-o serie de relatii succesive.

3. Determinarea si masurarea teritoriului de locuit al indivizilor si populatiei

Amintesc acest aspect, dar el se preteaza foarte bine la animale vertebrate. La insecte s-au facut cercetari la furnici, lacuste, unele coleoptere. Metoda este importanta pentru analiza competitiei si influenta densitatii. La insecte, teritoriul de locuit nu trebuie privit ca o simpla suprafata geografica, iar in conditii in care studiul poate fi facut riguros, pot fi detectate si modificarile datorate competitiei intra- si interspecifice, modificarea resurselor si modificarea comportamentului. Ca metoda, se pot folosi foarte bine o serie de tipuri de capcane (feromonale, Barber, luminoase, colorate, cu apa, etc), observatiile directe pe traseu sau o aparatura mai sofisticata adaptata la comportamentul speciei (radare, metoda GPS etc).

a. Metoda suprafetei minime Punctele de recaptura se pot marca pe o harta la o scara convenabila intinderii teritoriului si se pot face masuratori. Metoda are avantajul ca nu se face nici o referire asupra conformatiei teritoriului, acesta fiind considerat ca liniar

Suprafata se calculeaza prin unirea punctelor extreme (Fig. 5-17, a).

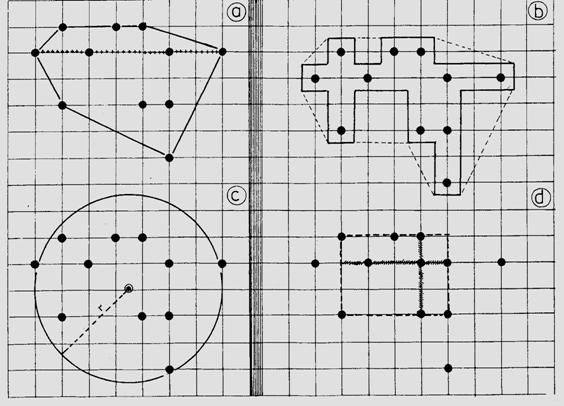
Fig. 5-17. Modalitati simple de determinare si masurare a teritoriului de locuit al unui individ sau a unei populatii, prin: metoda suprafetei minime (a), metoda fasiei de hotar (b), aprecierea lungimii teritoriului (+++++ A), metoda centrului de activitate (c), metoda suprafetei geometrice (d) (date din Southwood, 1966).

b. Metoda fasiei de hotar Se apropie de cea anterioara dar, in plus, se ia arbitrar o banda care se intinde si pe jumatatea domeniului capcanei vecine (Fig. 5-17, b). Metoda are doua variante marcate pe figura cu------ si +++++++ (ultima dand cele mai bune rezulate).

c. Lungimea domeniului Este distanta dintre cele mai indepartate capturi (marcare cu ++++++ in Fig. 5-17, a). Se mai poate ajusta, ca si la punctul anterior, prin includerea si a jumatate din distanta capcanei urmatoare.

d. Metoda centrului de activitate S-a pus in aplicare pentru a elimina unele dificultati legate de stabilirea fasiei si influenta capcanelor invecinate. Centrul de activitate este centrul geometric al tuturor punctelor de captura sau de observatii (Fig. 5-17, c). Se calculeaza astfel: se aplica punctele de captura pe o grila; fiecare punct are doua valori (una pe verticala si una pe orizontala); se insumeaza toate valorile de pe verticalagrilei si se impart la numarul de observatii obtinand o valoare medie; se procedeaza la fel si pe orizontala; cele doua valori medii vor fixa un punct care este centrul de activitate.

e. Metoda suprafetei geometrice. Se bazeaza pe punerea in evidenta, prin unirea pe grila a punctelor de captura sau observare situate la extremitatea a diua drepte perpendiculare dar in asa fel incat prin unirea a cat mai multe puncte de pe o latura, sa se formeze o figura geometrica clasica, a carei suprafata poate fi calculata matematic (Fig. 5-19, d).

f. Indicele domeniului de activitate Este o metoda simplificata a centrului de activitate dar se ia in considerare domeniul ca fiind circular iar distantele diferitelor puncte de recaptura reprezinta razele acestor cercuri (raze de recaptura). Unii autori iau in considerare un diametru standard ca diametru al cercului a carui raza este egala cu abaterea standard a valorii razelor de recaptura. Indicele domeniului de activitate (indice al centrului geometric al activitatii, este calculat dupa relatia:

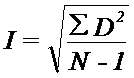
(N = numarul de observatii; D = diametrul de recaptura adica distanta fiecarui punct de recaptura sau observatie pana la centru si dublata).

3.6. Efectivul populatiei

Efectivul populatiei Se intelegea ca vor exista diferente mari in ceea ce priveste acest gen de studii la plante si separat la animale. Plantele fiind fixate implica si o precizie mai mare a datelor. Din acest punct de vedere ne vom referi mai mult la ecologia animalelor.

Dupa ce o specie tinta a fost evidentiata intr-un anume loc, orice studiu ecologic implica o prima intrebare de genul: cat este de mare este populatia acestei specii ?. Sau, care esdte efectivul sau ?.

Efectivul = numarul de indivizi (abundenta sau biomasa) la un moment dat de timp Efectivul este o marime relativa si empirica, iar aceasta relativitate a efectivului exprimat prin cifre decurge tocmai din metoda estimarii, cu ajutorul careia apreciem numarul de indivizi. De fapt prin metoda estimnarii se face un recensamant al indivizilor populatiei. Masura de precizie a valorii efectivului este in functier de marimea populatiei. Foarte rar exista populatii la care efectivul se aprecieaza prin numaratoare directa.

De cele mai multe ori ecologul apreciaza efectivul cu ajutorul probelor (esantioanelor). Metoda implica stabilirea unui plan initial dupa care din populatia totala se estrage un numar de prbe care contin un anumit numar de indivizi. In esenta procedeul consta in impartirea ariei ecosistemului in patrate. Marimea acestora este in functie de suprafata ecosistemului si de caracteristicile biologice si comportamentale ale speciei. Intr-un anumit numar de patrate (alese si aceste randomizat, pe baza numerelor intamplatoare), in momente precizate ale ciclului biologic se vor lua probe. Probele consta din inregistrarea numarului total de indivizi de pe acel patrat. Efectivul dintr-o asemenea unitate reprezinta o proba de populatie. Printr-un calcul simplu, se va estima efectivul populatiei:

Efectivul populatiei = [( suma frecventelor indivizilor in patrate / nr. patratelor cercetate ) x nr. total de patrate ]

Se poate deduce ca dupa aceasta metoda, pentru a aprecia un efectiv cat mai corect ar trebui sa presupunem ca populaia este prezenta in intregul ecosistem, iar media aritmetica a patratelor cercetate ar fi aproximativ-egala cu media aritmetica a patratelor necercetate. Dar se intampla foarte rar sa fie asa si de aici rezulta si erorile de estimare. Evitarea sau mai corect spus, diminuarea erorilor este posibila prin:

cunoasterea biologiei si comportamentului speciei, alegerea unei metode specifice de estimare, cunoasterea ecosistemului si a habitatelor existente. Exista insa si metode matematice de corectare a erorilor.

Biomasa. In esenta, aceasta reprezinta expresia cantitatii de organisme existente pe o unitate de suprafata sau volum. Biomasa poate fi evaluata in mai multe moduri:

a. prin cantarire directa (umeda sau uscata). Pentru uscare materialul biologic este expus la temperaturi ridicate pentru perioade variabile de timp, in functie de volum si calitate. Se mai practica si congelarea rapida;

b. exprimata prin cantitatea de energie inclusa i materia vie;

c. prin folosirea unor valori cantitative determinate initial cu ajutorul bombi calorimetrice;

d. pentru organisme mici si foarte mici, prin masurarea biovolumului la microscop si o incadrare a individuluiintr-o forma geometrica ce poate fi evaluata (se poate folosi si metoda fotografica

e. pe baza unor indici de estimare;

f. prin volumetrie;

g. prin expresii matematice traditionale (ex ecuatia de regresie a relatiei lungime - greutate) (Sample si colab., 1993).

Efectivul este deci o marime raportata la timp si la intregul spatiu ocupat de populatie.

Densitatea este numarul de indivizi (sau biomasa) raportata la o unitate de suprafata.

Fiind o marime variabila, densitatea are o valoare relativa. Din acest caz in practica ecologica densitatea este corectata cu abundenta

relativa (numarul de fluturi iregistrati/1 ora; numarul de cantece ale unei specii de pasari, inregistrate/5 min. etc).

Cand se estimeaza densitatea, pentru o anumita specie vom avea o densitate minima, o densitate maxima, o densitate medie. Se intalneste si termenul de densitate optima (= numarul de indivizi dintr-o unitate spatiala care asigura cea mai mare eficienta a populatiei in utilizarea resurselor mediului si o buna supravietuire ca rezultat al luptei pentru existenta). Densitatea optima poate sa nu coincida nici cu cea minima, nici cea medie, nici cea maxima.

Studiul populatiilor este marcat de 6 particularitati caracteristice: distributia spatiala a indivizilor, densitatea, rata intrinseca a cresterii naturale, ciclul de viata si piramida varstelor, rata sexelor, polimorfismul genetic. Aici ne vom referi doar la aspectul estimarii densitatii si marimii populatiilor, celelalte directii fiind abordate anterior.

Pentru estimarea densitatii exista multe modalitati dar 4 categorii sunt semnificative: masurari directe asupra populatiei, inregistrarea numarului pe traseu (metoda transectului), masurarea prin esantionaj (analiza capturilor), captura-marcare-lansare-recaptura, prin metode indirecte.

3.7. Modelul de distributie (dispersie) a populatiilor

Am facut anterior precizarea ca literatura ecologica engleza utilizeaza termenul de distributie pentru modul de repartitie a populatiilor de animale in ecosisteme. Literatura franceza (date in Frontier si Pichod-Vial, 1998) foloseste terminologia de distributie pentru a se referi la variabile aleatoare si frecventa lor (distributia caracterelor demografice ale indivizilor, distributia caracterelor demografice ale populatiilor etc), iar pentru modelul de distributie a populatiilor se foloseste terminologia de repartitie (o repartitie la scara mare: prin cartografierea unor suprafete mari ca in cazul studiilor de fitoplancton; o repartitie la scara mica = repartitia populatiilor si indivizilor in ecosistem = modelul de distributie a populatiilor din literatura engleza (pattern of population distribution) (Smith, 1974). In cele ce urmeaza cursul va adopta punctul englez de vedere dar si aici apar unele neconcordante. Unele lucrari fac referire la modele de dispersie (Collier si colab., 1974), dar se face precizarea ca sensul lui dispersion este diferit de cel de dispersal (miscarea organismelor in afara populatiei). Alte studii folosesc termenul de spacing (interval, distanta) vorbind despre pozitia membrilor unei populatii fata de vecini dar se uzeaza si de terminologia de distribution (Brewer, 1988).

Distributia se refera la modul de repartitie a caracterelor sau a organismelor (indivizi, specii) intr-un habitat (sol, apa, aer) sau la nivelul la care se fac prelevarile de probe. Despre modul cum o populatie (sau o parte a indivizilor ei) este distribuita si repartizata in spatiu (in ecosisteme) are influente considerabile asupra densitatii, a cunoasterii modelelor comportamentale, in vederea caracterizarii dinamicii si structurii populatiilor, iar in paralele, pentru alegerea celei mai corecte metode de sampling.

Exista 3 moduri de distributie a populatiilor (indivizilor) in spatiu: - la intamplare (Poisson, hazard, randomizat); - uniform (binomial pozitiva); - agregate (binomial negativa, aglomerat, contagios) (Fig. 5-18).

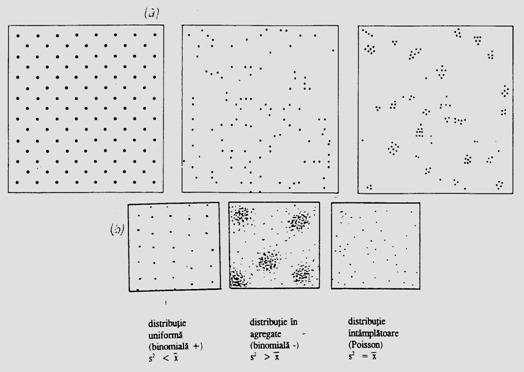
Fig. 5-18. Modelul de distributie a populatiilor (indivizilor) in spatiu. 1 - uniform (1a - uniform ideal; 1b - uniform relativ); 2 - intamplator (randomizat, Poisson); 3 -in agregate (dupa Smith, 1974; Stan, 1993).

a. - In distributia uniforma indivizii ocupa suprafete aproximativ egale (ex. arborii de aceeasi varsta intr-o padure). La animale, in schimb, este foarte rar intalnit un asemenea model si eventual numai acolo unde exista o competitie intensa intre indivizi, manifestandu-se o tendinta de dispersie (indepartare). O distributie uniforma este posibila in situatiile de competitie intraspecifica. De asemenea, daca sunt conditii relativ omogene ale factorilor de mediu, pe un teritoriu relativ omogen, se poate realiza o distributie relativ uniforma. Distributie uniforma ar putea fi la plante in cazul dispunerii coroanei sau a radacinilor sau la arborii din padure (ori plante de desert) in preferinta lor pentru umiditate (Beals, 1968).

b. - In distributia intamplatoare (Poisson, hazard, randomizata), repartitia este la intamplare (randomizata) si apare de asemenea rar (in conditii omogene de viata, populatia este subordonata unui singur factor (biotic sau abiotic), care si el la randul lui este distribuit tot intamplator. La acest model, se poate presupune ca intre indivizi exista doar 'indiferenta' (nici dispersie, nici agregare). Unele nevertebrate din padure, in mod special paianjeni, sunt caracterizate de un asemenea model de distributie (Kuenzler, 1958), molusca Mulinia lateralis din America de Nord, sau elanul (Bergerud si Manuel, 1969) caracterizat de o distributie intamplatoare a agregatelor de elani (grupuri aproximativ egale ca marime). Mai mult, unele studii sustin punctul de vedere dupa care o distributie randomizata este nereala in natura si ca ea va tinde spre una uniforma (Collier si colab., 1974), ca fiind o forma de trecere spre distributia in agregate.

c. - Pentru distributia in agregate (aglomerata, contagioasa) este caracteristica formarea grupurilor. Aceste grupuri pot fi mai mult sau mai putin numeroase, cu distributie intamplatoare. Apar in populatiile unde exista o competitie intensa, deci este determinata de comportamentul indivizilor sau de factorii ecologici. La randul ei, distributia agregatelor poate fi uniforma sau intamplatoare. Distributia in agregate este un raspuns al plantelor si animalelor la diferentele de habitat, la schimbarile de mediu si factori (zilnic sau sezonier), la modelul de reproducere si comportamentul social sau de agregare. Agregarea poate fi si accidentala la animale, dependent de sursa de hrana, umiditate, umbra, la un moment dat. La multe specii este o reflectare a comportamentului (gradul de toleranta sociala sau gregara) (asociat cu comortamentul de curtare, cu constructia cuibului, cu migrarea, cu definirea castelor si ierarhiilor). Distributia in agregate este caracteristica si omului (exista agregari urbane dar si zone opuse cu o mare dispersie; toate influenteaza potentialul reproductiv si rata cresterii).

Cercetarile ecologice in domeniul cunoasterii modelului de distributie sunt relativ complicate si implica o foarte buna cunoastere a biologiei si comportamentului speciilor. Exista multe puncte de vedere chiar din partea specialistilor. Unii sustin ca distributia uniforma este foarte rara in natura si ca atunci cand exista, este vorba de o distributie uniforma a agregatelor. Altii considera distributia randomizata ca nereala. Chiar si distributia in agregate depinde de densitatea populatiei si de marimea spatiului si poate depinde chiar de sansa.

Pentru o analiza corecta a modelului este necesara cunoasterea unor aspecte legate de specii, cum ar fi:

☼ - un comportament social determina speciile sa fie atrase unele spre altele deci sa induca un model in agregate;

☼ - organismele tind sa raspunda si la heterogenitatea mediului astfel ca unele se stabilesc in anumite medii, in timp ce altele sunt evitate;

☼ - stabilirea intr-un anume mediu poate fi intamplatoare dar heterogenitatea mediului poate induce o anumita rata a mortalitatii;

☼ - pentru specii cu capacitate locomotoare redusa, urmasii se dezvolta din oua dispuse in grupe, iar la plante, semintele sunt raspandite in general pe o suprafata relativ redusa; deci o dispunere in agregate impusa de un model comportamental; la plante agregarea este asociata cu natura semintelor si anexele care ajuta la propagare (semintele grele, mari, ale unor plante vor cadea in imediata apropiere a arborelui-mama in timp ce semintele usoare, cu aripioare, umbrelute sau alte dispozitive, vor fi transportate la distante mari; altele cu dispozitive speciale vor fi raspandite de catre animale; plantele agatatoare sau cu inmultire vegetativa determina de asemenea agregate;

☼ - vantul sau curentii de apa pot deplasa anumite organisme, pasiv, dar nerandomizat si astfel ele se pot aglomera in anumite medii care devin favorabile;

☼ - pe langa modelul comportamental, distributia trebuie analizata in relatie cu densitatea si cu factorii ecologici care influenteaza natalitatea si mortalitatea (daca de exemlu, rata mortalitatii este cunoscuta si o consideram dpendenta de densitate, atunci nu este corect sa consideram o distributie randomizata ca fiind echivalenta cu o populatie de aceeasi marime dar in care indivizii sunt puternic agregati);

☼ - mai exista un aspect: multe organisme sunt sesile sau cu o capacitate redusa de miscare. Toate animalele sesile si chiar si toate plantele, au o perioada scurta din viata lor cand se pot deplasa s-au sunt deplasate pasiv, pe distante scurte; cand facel studiul modelului de distributie, noi neglijam aproape in totalitate aceasta faza din viata lor si ne referim doar la un model, dupa ce specia s-a stabilit in mediul respectiv;

☼ - speciile de animale cu stadii puternic deosebite intre ele, in ciclul biologic (ex. insectele) au modele de distributie diferite. In stadiul de ou distributia este initial una uniforma (datorita feromonilor de ovipozitare) desi initial se credea ca este intamplatoare; la unele specii ponta este dispusa in ooplaci mai mari iar dispersia se realizeaza ulterior, pe parcurs ce larvele cresc. Modell de distributie al adultilor poate fi total diferit de cel al larvelor (larvele sunt dependente de baza trofica, in timp ce adultii, dataorita capacitatii de zbor, pot avea un alt model de distributie (vezi detalii in Stan, 1993).

☼ - modelul de distributie apare asociat cu nevoia de supravietuire. Astfel organizarea (distributia) in grupuri ofera sanse mai mari de supravietuire decit in cazul speciilor solitare (ex. haitele, cardurile, bancurile de pesti). Unele specii se agrega noaptea sau in sezonul friguros pentru a rezista conditiilor nefavorabile;

☼ - agregarea este asociat cu asigurarea unui optim de densitate. Sunt specii la care optimul de agregare este la densitatile cele mai mici posibile; la alte specii acest optim este undeva intermediar, intre o densitate mai mica si una mai mare (Smith, 1974).

Un alt aspect interesant este prezentat de catre Pielou (1969). Sunt puse in discutie 3 situatii:

☻ - organisme care traiesc numai in anumite unitati discrete de mediu, recunoscute intr-o anumita zona sau suprafata; astfel, anumite probe pentru anumite specii nu se pot lua decat din spatii stricte si bine delimitate (sub roci, crapaturi etc); larvele unor specii de insecte monofage se afla numai pe fructele sau frunzele unei specii gazda ce constituie baza trofica a speciei; aceste unitati diecrete pot fi considerate chiar unitati de sampling (probe);

☻ - la polul opus celui prezentat anterior sunt specii care sunt imprastiate peste tot, iar densitatea lor variaza din loc in loc intr-o aceeasi maniera; este cazul populatiilor de colembole (Insecta: Apterygota) din litiera padurilor, ceea ce face dificila alegerea suprafetelor de proba care sa ilustreze modelul real (in aceasta situatie metoda trebuie aleasa in asa fel incat sa se aleaga de ex. probe mai mari pe suprafete mari); acesta este si cazul studilor de distributie la populatiile de plante care se incadreaza tot aici;

☻ - o a treia situatie se refera la formele (grupari de organisme) extrem de mari (bancuri de animale, suprafete marine acoperite de alge sau diatomee care sunt greu de studiat si incadrat, iar pe de alta parte, sunt frecvent evitate.

4. Dinamica populatiilor

4.1.Dinamica populatiei in sisteme inchise si deschise. Cazuri speciale in dinamica populatiilor (natalitatea si mortalitatea excesiva, stress-ul si sindromul adaptativ)

Succesiunea starilor numerice ale populatiilor definesc dinamica acestora. Astfel, sub aspect formal dinamica este o succesiune de stari aleatorii. Am aratat anterior ca doar intr-un sistem inchis, marimea populatiei depinde de natalitate si respectiv de mortalitate. In realitate, pentru a analiza dinamica, populatia trebuie privita ca un sistem deschis unde intervin si imigratia, respectiv, emigratia, dar si alti parametrii. Monitorizarea continua permite inregistrarea modificarilor de densitate (ca numar de indivizi sau ca biomasa). Trecerea de la o stare la alta depinde mereu de starea anterioara sau chiar de unele evenimente care pot sa apara intamplator, dar au unfluenta asupra dinamicii populatiei respective. Este evident ca fiecare stare prezenta are la baza o succesiune de stari trecute si realizate. Astfel, efectivul populatiei la un moment dat este rezultatul logic al unor evenimente (natalitate, mortalitate, emigrare, imigrare), chiar daca in prezentarea curbei dinamicii, cercetatorul nu le specifica.

Pe de alta parte, dinamica nu este predeterminata mereu de tarea initiaa ci poate di dependenta de o serie de factori ecologici care influenteaza sincron, cresterea si supravietuirea populatiei la un moment dat al existentei sale. Asemenea procese se numesc stohastice (aleatoare, intamplatoare) [gr. stokhastikos = presupus, conjunctural, posibil].

Vom urmari in continuare modele de crestere a populatiilor. Nici curba exponentiala (geometrica) nici cea logistica (sigmoida) nu pot lamuri complet domeniul cineticii populatiilor in mediul lor natural. Lipsa datelor concrete ca urmare a prelevarilor de probe, precum si nefinalitatea gasirii unor relatii matematico-statistice adecvate fac dificila gasirea unor solutii cu statut de concluzii.

Dinamica populatiei animale nu poate fi inteleasa numai prin explicarea unor concepte fizice. In biologie; evolutia nu poate fi dedusa doar din starea initiala. Cunoasterea acestei stari cat si a altor paramterii, nu este suficient pentru a prognoza o evolutie ulterioara.

Interpretarea matematica a datelor arata ca in ceea ce priveste dinamica unei populatii, variatiile pe parcurs oscileaza in jurul unei valori medii, deci dinamica ar tinde spre o stare stationara. Populatia ecologica functioneaza ca un proces stationar in sensul ca pe parcurs, la un anume punct din curba dinamicii valoarea densitatii nu depinde de densitatea initiala de la care s-a plecat ci de raportul dintre natalitate si mortalitate, dintre imigratie si emigratie sau factori directi si indirecti de care depind aceste procese. Se vorbeste astfel de un proces stohastic, de tip markovian, cu stari succesive ca urmare a unei reactii in lant (proces tip Feller) (Stugren, 1975).

In lumea vie, asemena situatii de stari izolate, de abordare a unei populatii ca sistem inchis, nu este posibila. Populatia este un sistem deschis, care comunica cu alte populatii prin "schimb de indivizi" (imigratii, emigratii). In acest caz, cresterea populatiei este rezultatul natalitatii + imigrarea, iar scaderea nivelului populatiei depinde de mortalitate + emigrarea. Deci populatia la un anumit moment t+n nu este consecinta starii din momentul t₀. Dinamica unei populatii in sistemele deschise este redata de functia lui Bartlett (Bartlett, 1955).

Dinamica populatiilor este asadar un proces variabil, cu modificari in functie de an sau sezon dar, la majoritatea speciilor se constata a fi un fenomen normal si caracteristic viului, al interrelatiei permanente dintre acesta si factorii ecologici, interni si externi.

Exista insa la nivelul viului, situatii in care unele specii inregistreaza fluctuatii (ale abundentei sau biomasei) care ating din cand in cand valori maxime supranormale, dupa care se poate observa o scadere care poate fi cu mult sub starea normala obisnuita. Aceste situatii sunt considerate similare proceselor cvasi-stationare din fizica si matematica. Fenomenul sugereaza ca in timp se inregistreaza oscilatii care evidentiaza diferente mari intre doua momente de timp (ex. unele mamifere si pasari nordice, ciclurile rozatoarelor, oscilatiile speciilor pradatoare, ciclurile bancurilor de pesti etc).

Dinamica populatiilor este asadar un fenomen ciclic si cvasi-stationar caracterizat de existenta unui interval fix intre doua asemenea momente succesive de supermaxim numeric (se repeta la acelasi interval de timp (Elton, 1942; Lack, 1954):

- ciclul de 10 ani la specia Lepus americanus (iepurele nord-american), inclusiv specia de pradator specific - Lynx canadensis (rasul american), din Nordul Americii si Canada;

- ciclul de 4 ani la specii din genul Microtus (soareci), inclusiv speciile pradatoare asociate din padurile de foioase din taigaua euro-asiatica;

- ciclul de 4 ani la specii din genurile Lemmus si Dicrostonyx (lemmingi), inclusiv speciile de pradatori, caracteristice tundrei din Europa, Asia si America de Nord.

Natalitati si mortalitati excesive. Sunt doua fenomene care la anumite intervale de timp pot afecta semnificativ abundenta populatiilor, aspect care poate fi evidentiat in studiul dinamicii. Practic exista o varietate de cauze care pot influenta cele doua procese. Cele mai credibile sunt cele legate de cantitatea de hrana si daunatori specifici. Alte studii considerau ca variatia ciclica a radiatiei solare, in ritmul anilor cu pete solare (manifestari ale exploziilor si furtunilor solare), este cauza acestor procese biologice. Fapt ulterior infirmat, sau cel putin, pentru anumite specii, el nu a fost dovedit. Indirect toate tipurile de radiatii electromagnetice care ajung pe pamant induc anumite modificari, dar nu influenteaza in asemenea masura fiziologia organismelor. Este adevarat ca plantele isi regleaza ciclurile de dezvoltare in raport cu ciclurile factorilor meteorologici. De exemplu, in zonele nordice, cand este hrana suficienta in verile calde, care alterneaza periodic cu verile reci, productia de fructe a plantelor este maxima. Fiind hrana multa si numarul rozatoarelor este de asemenea mare sau chiar excesiv (Kalela, 1961).

In cazul mortalitatii sunt mai multi factori posibili: foamete, factori de mediu excesivi, epidemii, pradatori. La populatii de rozatoare de exemplu, se pare ca nici unul dintre acestia nu are o importanta atat de mare precum relatiile dintre indivizi, de lupta pentru suprematie, dominatie sau existenta (Chitty, 1952). Agresivitatea dintre indivizi din perioadele de suprapopulare excesiva pot duce la o diminuare numerica excesiva. La Microtus sp. mortalitatea este mai mare primavara comparativ cu iarna cand populatia este mai mult expusa si frigului si daunatorilor.

Pierderi mici de indivizi sunt frecvente in orice populatie si sunt datorate variatiilor la nivelul factorilor climatici, factori interni (varsta, hrana), factori populationali (relatii intra- si interspecifice), boli. Mortalitatea ale carei cauze au fost sugerate de catre Chitty (1952) nu a fost insa verificata la toate speciile de rozatoare. Pentru alte specii a fost semnalata "boala de soc", un fenomen atipic, in care mortalitatea aparea cauzata nu de afectini evidente ci de un asa-zis fenomen de epuizare subita fara sa fie detactate infectii la nivelul organismului sau alte modificari semnificative le nivelul proceselor fiziologice. Unii specialisti au denumit acest fenomen sindrom adaptiv sau adaptabilitatea organismului (Selye, 1956), fiind in realitate vorba de o reactie adecvata a organismelor in urma unor actiuni puternice interne si externe (gen stress) la care organismul se apara in general, pe cale fiziologica-biochimica sau pe cale ecologico-functionala (Fig. 5-19), de-a lungul unui proces constituit din 3 faze importante: faza de alarma, faza de rezistenta si faza de epuizare.

Fig. 5-19. Mecanismul biochimic (a) si cel ecologico-fiziologic (b) al sindromului adaptativ (dupa Stugren, 1975).

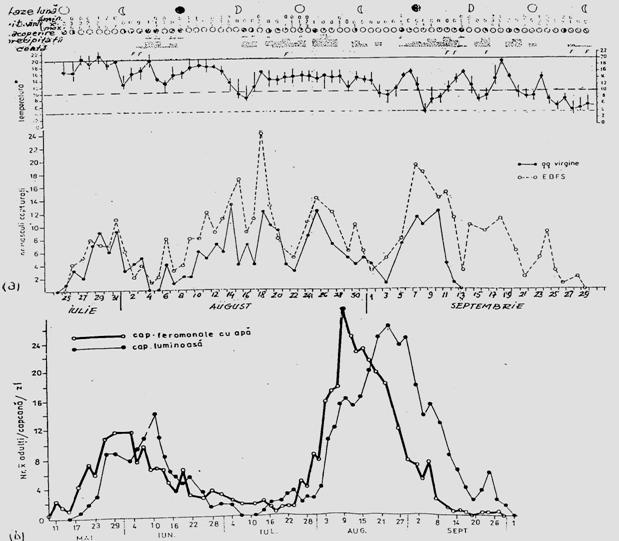
Fig. 5-20, a, b. Dinamica abundentei la populatiile de Xestia c-nigrum (a, b) si Mamestra brassicae (c, d), evidentiata in diferite perioade de timp, pe baza datelor de captura cu ajutorul capcanelor feromonale si luminoase. (a) - dinamica sp. Xestia c-nigrum analizata corelat cu evolutia factorilor climatici (Cluj; 1985) pe baza datelor de captura cu capcane feromonale cu femele virgine si cu extract brut de feromon sexual; (b) - dinamica abundentei pentru populatiile de Xestia c-nigrum pe baza datelor de captura cu capcane feromonale adezive si capcane feromonale cu apa (Cluj-Someseni, 1989); (dupa Stan, 1990; Stan si colab., 1986, 1990, 1992).

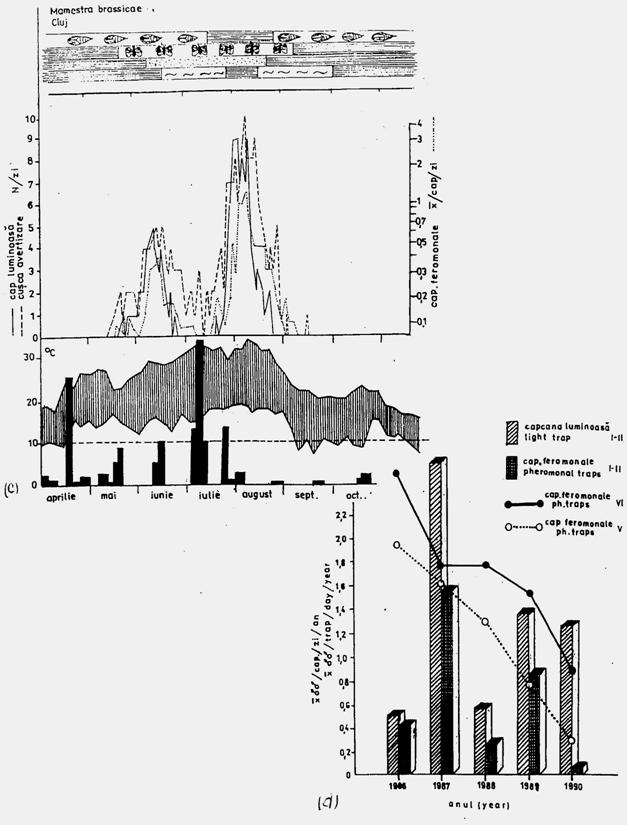
Fig. 5-20, c, d. Dinamica abundentei la populatiile de Xestia c-nigrum (a, b) si Mamestra brassicae (c, d), evidentiata in diferite perioade de timp, pe baza datelor de captura cu ajutorul capcanelor feromonale si luminoase. (c) - bioclimograma speciei Mamestra brassicae in zona Cluj (1988); (d) - evolutia nivelului populatiilor ecologice de Mamestra brassicae din zona Cluj (1986-1990), in doua tipuri de ecosisteme (natural si agroecosistem), pe baza datelor de captura zilnica (dupa Stan, 1990; Stan si colab., 1986, 1990, 1992).

In populatiile de rozatoare declansarea stress-ului este rezultatul unui comportament agresiv excesiv, fixat genetic si posibil influentat de factorii externi. Suprapopularea determina intensificarea nervozitatii si luptelor pe viata si pe moarte. Stress-ul determina mortalitatea pe urmatoarele cai:

- incapacitatea de aparare pe cale biochimica in faza de epuizare;

- aparitia unor boli incurabile (hipertensiune, scleroza, diabet etc);

- scaderea rezistentei in fata infectiilor;

- diminuarea capacitatii de a mobiliza mecanismele de termoreglare in momente in care factorii climatici devin extrem de nefavorabili

4.2. Modificarea numarului si biomasei in populatii. Curba de zbor

Simplist, dinamica populatiei (populatiilor) este vizualizata cu ajutorul unor curbe reale prin care este prezentata dinamica numarului (abundentei) sau biomasei. Folosite in studiile ecologice la pasari si insecte, poarta denumirea de curbe de zbor (Fig. 5-20).

4.3. Parametrii dinamicii populatiilor. Rata natalitatii si rata mortalitatii

Populatia fiind constituita din totalitatea indivizilor unei specii are caracteristici si particularitati dependente de acestia. In timp si spatiu indivizii se nasc si mor, iar intre cele doua extreme, cresc, se dezvolta si se reproduc. Indiferent de aceasta, daca mediul este favorabil populatia va exista.

Indivizii pot intra intr-o populatie prin imigrare sau datorita fenomenului de nastere si parasesc populatia prin mortalitate si emigrare (Fig. 5-21). Daca populatia nu se schimba prin emigrari si imigrari atunci dinamica sa este caracterizata de urmatorii parametrii: rata natalitatii, rata mortalitatii, rata cresterii numerice si ecuatia de crestere.

Orice rata este un raport intre o crestere sau scadere si marimea intreaga fata de care se face raportarea, intr-o unitate de timp.

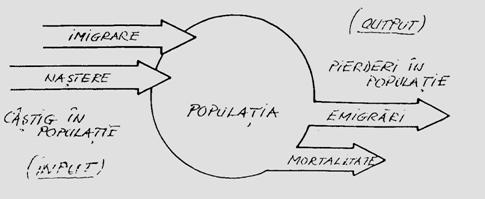
Fig. 5-21. Reprezentarea scmematica a factorilor care modeleaza marimea unei populatii (dupa Brewer, 1988).

Daca excludem imigrarea si emigrarea (lucru usor de realizat in laborator), atunci marimea populatiei este dependenta de natalitate si mortalitate. Numarul de indivizi care apar intr-o populatie, ca rezultat al reproducerii (nastere, germinare, diviziune, inmugurire rtc), raportat la o anumita durata de timp constituie rata natalitatii (m_x). Numarul de indivizi care dispar din populatie, prin moarte, intr-o anumita unitate de timp constituie rata mortalitatii (q_x).

In cazul mortalitatii vorbim de rata bruta a mortalitatii care reprezinta numarul indivizilor morti intr-o durata de timp la nivelul unei populatii. La fel ca si in cazul natalitatii in cercetari ecologice se face referire la un indice mai corect - rata mortalitatii specifica varstei (q_x) (= numarul de organisme de varsta x morti intr-o unitate de timp raportat la numarul de indivizi de varsta x care au trait la startul perioadei de timp). Reprezentarea lui q_x se poate face pornind de la o curba = curba de supravietuire (Fig. 5-22, a). Numarul de indivizi de aceeasi varsta (cohort), la orice varsta x, se noteaza cu l_x. Daca se ia ΔN = numarul de organisme moarte intr-o unitate mica de timp = Δt, rata mortalitatii specifica varstei poate fi interpretata grafic ca raportul dintre ΔN si Δt. Acest raport este denumit d_x (d_x = ΔN / Δt). Dar cum intervalul Δt este foarte mic raportul apropie inclinatia curbei l_x la x. Raportand pe d_x la l_x rezulta rata mortalitatii / individ de varsta x.. Acesta fiind chiar coeficientul q_x:

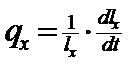
Aceata relatie reprezinta rata mortalitatii instantanee varstei specifice.

Atunci cand se fac estimari ale marimii populatiei nu este suficient de apreciat numai supravietuitorii ci este necesara adaugarea aditionala a indivizilor tineri care se nasc. Daca natalitatea se refera concret la indivizii tineri care apar pe o unitate de populatie, intr-o unitate de timp, se vorbeste despre rata bruta a natalitatii. La nivelul unei populatii complete cand se tine cont si de mortalitate, natalitatea este exprimata ca o rata specifica unei varste (rata natalitatii specifica varstei; m_x ; m_x = media numarului de femele produse de o femela apartinand unei clase de varsta x, pe unitatea de timp). Calcularea lui m_x este similar cu cea a lui q_x, dar pe baza relatiei dintre varsta (abscisa) si media cumulata a numarului de urmasi produsi de o femela de la varsta 0 la varsta x (ordonata) (Fig. 5-22, b). Daca Δx este egala cu o unitate de timp, atunci Δy/Δx = m_x. Daca intervalul de timp si deci Δx devin din ce in ce mai mici Δy de asemenea va descreste, iar raportul Δy/Δx se va apropia de inclinatia liniei la x, iar inclinatia liniei este un simplu raport dy / dx ceea ce reprezinta chiar coeficientul ratei natalitatii (m_x). Deci:

☺ - Variatii in modul de estimare la rata natalitatii (aici notata cu Q_n)

Este raportul dintre numarul de indivizi nascuti (n) intr-o unitate de timp si efectivul populatiei (N₀):

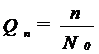
La insecte intervin unele aspecte aparte. Astfel, pe un interval scurt, Q_n va fi exprimata de raportul Y_t/N₀:

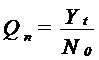
Y_t = Nr. total urmasi produsi in timpul t

N₀ = N_ou + N_L + N_P + N♀♀_IS + N♀♀_MS + N♀♀_Pr + N♂♂

(N_ou - nr. oua depuse; N_L - nr. larve; N_P - nr. pupe; N♀♀_IS - nr. femele imature sexual; N♀♀_MS - nr. femele mature sexual; N♀♀_Pr - nr. femele post-reproducere; N♂♂ - nr. masculi).

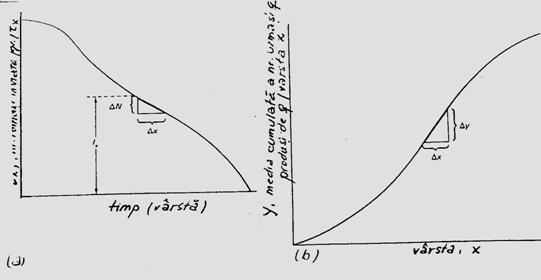
Fig. 5-22. (a). Ilustrarea modului de estimare a coeficientului ratei mortalitatii cu ajutorul curbei de supravietuire. (b). Modalitate de estimarea a ceficientului ratei natalitatii (detalii in text) (dupa Collier si colab., 1974).

Din relatia de mai sus se poate deduce ca influentele care afecteaza rata natalitatii (Q_n), pe un interval scurt de timp, depind de ponta depusa la nivelul populatiei.

Pentru informare, sintetizand factorii care influenteaza rata natalitatii, acestia sunt:

- fecunditatea femelelor (factor de importanta primara in dinamica populatiilor);

- fertilitatea femelelor;

- rata sexelor (determina proportia femelelor in populatie, deci si fecunditatea si fertilitatea; rata sexelor este modificabila in timp prin diferenta intre durata de viata a celor doua sexe);

- prezenta femelelor nereproducatoare (acestea determina implicit o scadere a duratei de viata, deci o modificare in timp a ratei natalitatii).

☺ - Variatii in modul de estimare la rata mortalitatii (aici notata cu Q_m)

Este raportul dintre numarul de indivizi morti (m) intr-o unitate de timp si efectivul populatiei (N₀):

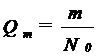
La insecte, ca si in cazul ratei natalitatii, s mortalitata afecteaza toate stadiile (ou, larva, pupa, adult) iar particularitatile specifice si factorii de mediu ce actioneaza la nivelul fiecarui stadiu au valoare deosebita pentru aprecierea ratei mortalitatii. De aceea si Q_m poate fi exprimata printr-o relatie de tipul:

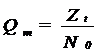
(Z_t = nr. total de urmasi morti in timpul t; N₀ = ac. explicatie ca in relatia)

Intr-o populatie, mortalitatea poate fi cauzata de: varsta, vitalitatea scazuta, accidentele (ex. proasta functionare a mecanismelor de maparlire,deformari la aripile adultilor, etc), conditiile fizico-chimice, boli naturale, pradatori, paraziti, agenti patogeni, hrana, uscaciunea, canibalismul, diminuarea capacitatii de refugiu in fata factorilor nefavorabili.

In cercetarile efectuate asupra populatiilor animale sunt importante datele furnizate de studiul ciclului biologic sau tabelul de viata (life table) care reprezinta si o ilustrare a structurii de varsta a populatiei la un moment dat. Este in realitate un "tabel al natalitatii si mortalitatii" deoarece cuprinde date statistice referitoare la mortalitatea si supravietuirea in populatie. Altfel spus este o transpunere tabelara a parametrilor statistici ai populatiei (Smith, 1974; Collier si colab.,1974; Brewer, 1988; Stiling, 1996) considerand mortalitatea ca probabilitate de viata sau ca rata a mortalitatii (Davis, 1960).

Iata de exemplu cativa coeficientii si indicii necesari studiului cresterii populatiei unei specii, inclusi in cadrul unui tabel caracteristic (Tabelul 9). Acesta este "varianta statistica" a tabelului clasic de ilustrare a ciclului de viata (Tabelul 9-bis).

Tabelul 9

Coeficienti implicati in studiul ciclului biologic al unei specii (date din Brewer, 1988).

* - varsta poate fi reprezentata si pe clase de varsta

Un asemenea tabel poate fi mai detaliat incluzind si alti parametrii (Tabelul 10). Iata acesti parametri (dupa date din Stiling, 1996):

x = intervalul de varsta (ani);

n_x = numarul de supravietuitori la inceputul intervalului de varsta x;

x' = varsta ca de deviatie din durata medie de viata;

dx = numarul de organisme muribunde intre inceputul intervalului de varsta x si inceputul intervalului de varsta x + 1;

l_x = proportia de organisme supravietuitoare la inceputul intervalului de varsta x;

q_x = rata mortalitatii intre inceputul intervalului de varsta x si inceputul intervalului de varsta x + 1;

e_x = media estimata pentru organismele vii la inceputul varstei x.

Tabelul 9 bis

Ilustrarea ciclului biologic la o specie de insecta cu metamorfoza holometabola, pe baza unor studii autecologice de crestere in conditii de laborator, pe dieta artificiala (d-152-V), in functie de temperatura (dupa Stan si colab., 1998)

Tabelul 9-bis continuare

- (^oC 0,5 ^oC); ² Cv = coeficient de variatie; ³ - durata stadiilor in zile ( eroarea standard; aceeasi litera indica diferente nesemnificative intre variante (D'sNMRT; P = 0,05); 4 - numarul adultilor care au iesit din pupe; ⁵ - numarul mediu de oua depuse/femela + numarul mediu de oua ramase in ovare, dupa moartea femelei; ⁶ - % de oua fertile din totalul de oua / femela; ⁷ - numarul de larve tinere iesite din ouale fecundate; NS = date nesemnificative

d_x poate fi calculat din cei 2 termeni adiacenti din coloana n_x (n_x si n_x+1):

n_x+1 = n_x - d_x (spre exemplificare conform datelor din Tab 8: n1 - n0 - d0 = 1000 - 199 = 801);

cum q_x poate fi calculat din noile valori d_x si n_x, atunci q_x = d_x / n_x

(ex. cf. Tab. 8: [q₂ = d₂ / n₂ = 13 / 789 = 0,0165];

l_x poate fi calculat din n_x si n₀; l_x = nx / n₀ (ex. cf. Tab. 5 [l₃ = n₃ / n₀ = 776 / 1000 = 0,776];

Pentru a facilita calcularea lui e_x, tabelul mai are 2 parametrii: T_x si L_x. Prima operatiune in favoarea estimarii lui e_x, porneste de la obtinerea numarului de animale vii in fiecare interval de clasa de varsta, pe baza valorilor lui n din clasele de varsta x si x + 1 (ex. cf. Tab. 8: [L₃ = (n₃ + n₄) / 2 = (776 + 764) / 2 = 770]

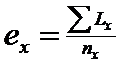
(ex. cf. Tab. 8: [e₁₀ = (174 + 51 + 4,5 + 1,5) / 252 = 0,92]

Tabelul 10

Ciclul de viata la specia Ovis dalli bazat pe cunoasterea varstei la care au murit 608 exemplare (din cele 1000 luate in studiu). Durata medie de viata a fost de 7,09 ani (semnificatia parametrilor este data an text) (date dupa Murie, 1944; din Stiling, 1996).

4.4. Cresterea populatiei. Modele de crestere: cresterea exponentiala, cresterea logistica, von Bertallanfy, Gompertz

4.4.1. Cresterea populatiei. Rata intrinseca si rata finita a cresterii

Definim o populatie ca un grup de organisme care apartin unei aceleeasi specii si ocuun anume spatiu la un moment dat. Atunci cand este necesar a compara diferite populatii, este nevoie de evaluarea si estimarea unor atribute si parametrii care caracterizeaza o anume populatie. Cei mai importanti sunt:

☼ - densitatea = marimea populatie raportata la o unitate de spatiu;

☼ - natalitatea sau rata natalitatii = rata la care sunt adusi in populatie noi indivizi, prin reproducere;

☼ - mortalitatea sau rata mortalitatii = nivelul de indivizi care sunt pierduti din populatie ca urmare a mortalitatii;

☼ - dispersia (dispersal) = rata in care indivizii imigreaza intr-o populatie sau emigreaza din populatie;

☼ - distributia (dispersion) = modul in care indivizii sunt distribuiti in spatiu. Exista 3 moduri clasice:

(a) - distributia randomizata (intamplatoare) = probabilitatea ca un individ sa fie intr-un anume loc este egala cu probabilitatea de a ocupa un alt loc;

(b) - distributia uniforma = in care indivizii sunt distribuiti in mod mai regulat decat in distributia randomizata; de ex. porumbul in cultura de porumb;

(c) - distributia grupata (in agregate) = modelul cel mai comun existent in natura, in care indivizii sunt distribuiti in mod neregulat;

☼ - repartitia claselor de varsta = proportia indivizilor de diferite virste in populatie

In conditiile in care cercetatorul dispune de suficiente date referitoare la ciclul biologic si cunoaste varsta specifica a reproducerii, pot fi determinate o serie de caracteristici ale cresterii populatiilor. Cresterea sau declinul populatiei depinde de distributia ratei natalitatii si mortalitatii in relatie cu varsta, plus o distributie aditionala care reprezinta frecventa relativa a indivizilor din populatie, tot in relatie cu varsta (distributia varstei).

Cel mai folosit index al cresterii populatiilor este rata instantanee de schimb a marimii populatiilor/individ (k):

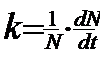
Paramterii relatiei se deduc din Fig. 5-23. Marimea populatiei in functie de timp este marcata de o curba de crestere iar inclinatia acestei curbe reprezinta rata cresterii populatiei. ΔN = rata neta a cresterii intr-un interval mic de timp = Δt

Fig. 5-23. Reprezentare grafica a relatiei dintre marimea populatiei si timp, pe baza curbei de crestere a populatiei. Rata instantanee a marimii populatiei se deduce din reprezentarea grafica. ΔN = rata neta a cresterii; Δt = intervalul mic de timp (dupa Brewer, 1988).

☻- rata intrinseca de crestere sau rata infinita (infinitesimala de crestere (r), este diferenta dintre rata natalitatii si rata mortalitatii. Deci, corect este sa se scrie:

r = q_n - q_m sau dupa notarea internationala: r = m_x - q_x

si nu: r = n - m care este coeficientul cresterii numerice. Cu acest gen de rata se poate lucra cu rezultate bune, in studiul populatiilor de mamifere, pasari sau la om.

In conditiile in care l_x, (= proportia de organisme supravietuitoare la inceputul intervalului de varsta x), m_x (= rata natalitatii) si distributia varstelor sunt stationare, rata de crestere a populatiei/individ este o constanta, iar populatia creste exponential.

Aceasta rata constanta a cresterii populatiei este simbolizata prin r. Sa mai amintim aici ca r defineste rata intrinseca de crestere in ecuatia diferentiala pentru cresterea populatiilor, intr-un mediu nelimitat si este dedusa din relatia:

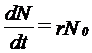
sau forma integrata

(N₀ = marimea populatiei initiale)

(e = baza logaritmului natural; e = 2,718)

(Ex. 10 exemplare de Lemna sp. - lintita, se dezvolta pe o durata de 4 zile; cunostem ca r = 0,20/zi;

N₄ = 10 x e ^{(0,2 x 4)} = 10 x 2,2 = 22

(dupa 4 zile populatia de Lemna va fi de 22 sau 23 indivizi)

Pentru calcule relatia de mai sus se poate scrie:

ln N_t = ln N₀ + rt

iar

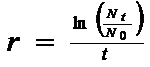
(presupunem ca populatia unei specii a crescut ca numar de la 40 indivizi la 426, pe durata a 3 ani. Daca consideram ca cresterea populatiei in aceasta perioada a fost exponentiala, atunci:

Rata intrinseca de crestere este rata de crestere per unitate in conditii fizice specifice, in spatiu nelimitat unde nu este nevoie sa se ia in considerare efectul cresterii densitatii. Multi autori s-au referit la acest concept sub denumirea de potential biotic (prin combinarea ratelor fecunditatii, sexelor si supravietuirii), indice de mediu (ca o masura relativa a stabilitatii mediilor, dar fara a prezenta rata de crestere in diferite conditii de mediu) sau indice combinat (insumand numarul de oua depuse, rata de supravietuire a stadiilor imature, rata de dezvoltare si rata sexelor)(aut.cit in birch

Studiul lui r s-a facut prin metoda de determinare directa, la specii de insecte cu o singura perioada de ovipozitare si care depun toate ouale repede (birch

Orice studiu despre rata de crestere a populatiilor este incomplet fara referire la distributia varstelor in populatie (si legat de aceasta, a capacitatii femelelor de a produce urmasi). O populatie are in realitate un anumit program al varstei atat pentru fecunditate cat si pentru mortalitate. Daca ar exista o populatie cu un program constant al varstei pentru fecunditate si pentru mortalitate, populatia va creste la o rata dN/dt = rN (deci parametrul r se refera la o populatie cu o distributie stabila a varstei). Ideea aceasta a fost vitala in statistica. In oricare alt fel de populatie, rata cresterii variaza in timp pana se obtine o distributie stabila a varstei. Referitor la aceasta, se poate pune intrebarea: care este rata de crestere pentru N₀ adulti proaspat emersi, intr-un spatiu nelimitat?. Aceasta rata va varia in timp pana cand populatia va avea o distributie stabila a varstelor. Pe de alta parte, maximul ratei care se poate mentine pe o perioada nedefinita de timp este data de rata de crestere intr-o populatie cu o distributie stabila a varstelor. Aceasta rata este deci o capacitate intrinseca de crestere a organismului.

Toate acestea au determinat pe unii specialisti ecologi in studiul populatiilor de insecte sa respinga forma exponentiala a ecuatiei de crestere, abordand rata de crestere ca un fenomen discontinuu. Totusi, rata de crestere ramane expresia cea mai buna pentru studiul cresterii populatiilor in spatiu nelimitat, dar ea singura nu este totusi satisfacatoare. Astfel, o etapa urmatoare a fost calcularea ratei de crestere tinand cont de varsta specifica a fecunditatii si rata de supravietuire, observata in conditii distincte (rata fecunditatii se considera proportia in care sunt depuse ouale: sunt inca discutii daca fecunditatea reprezinta numarul de oua depuse de o femela sau reprezinta numarul de oua depuse + numarul de oua din ovare, inregistrate la moarte). Considerand fecunditatea ca numar de oua depuse, apar alte aspecte: unele sunt nefertile, altele nu eclozeaza (in acest caz, acestea vor fi incluse in rata mortalitatii stadiului de ou). De fapt, unii ecologi si folosesc expresia de rata fertilitatii pentru rata natalitatii. Apoi, fecunditatea si rata de supravietuire variaza cu densitatea, deci valoarea lui r se poate calcula si la diferite densitati. Semnificatia particulara a lui r este in situatia unei fecunditati si rate de supravietuire, maxime, atunci si densitatea este optima si exista un maxim posibil al ratei de crestere, in cadrul unor conditii fizice definite. Aceasta zona poate fi considerata ca o zona optima (acceptiunea lui optim este uneori arbitrara; optim nu implica intotdeauna si un avantaj in crestere, la un maxim posibil al ratei). Rata maxima intrinseca de crestere are importanta din doua puncte de vedere:

- necesara 'ca termen', in ecuatiile matematice ale populatiilor (Lotka, Gausse, Voltera);

-importanta practica (pentru studiul temperaturii, umiditatii, densitatii, competitiei interspecifice, care modeleaza zona optima)

☻- rata finita de crestere (λ), este necesara in studiul populatiilor de insecte, ea reprezentand numarul de timpi necesari pentru multiplicarea populatiei pe o anumita unitate de timp. Deci, intr-o populatie care creste exponential, daca exista N_t indivizi la timpul t , in urmatoarea unitate de timp, rata de crestere va fi:

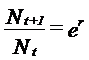
sau

Deci, rata finita (limitata ) de crestere este antilogaritmul natural al ratei intrinseci de crestere (r) sau reciproca, rata intrinseca de crestere este logaritmul natural al lui λ.

4.4.2. Cresterea exponentiala

Daca in timpul 0 se porneste de la un individ care se tot multiplica din timp in timp (1, 2, 4, 8, 16, 32, 64, 128.), multiplicarea este de tip exponential. Daca intr-o populatie exista acest tip de crestere, in care populatia creste mereu, este vorba de o crestere exponentiala (vezi Fig. 5-24).

Acest tip de crestere depinde de potentialul biotic al speciei, de marimea populatiei (cand potentialul este redus si rata de crestere este redusa). Cresterea exponentiala este rara (cazul bacteriilor sau a altor microorganisme).

In acest tip de crestere, la momentul t+1, marimea populatiei este data de relatia:

N_t+1 = R₀N_t

(N_t = marimea populatiei de femele in generatia t; N_t+1 = marimea populatiei de femele in generatia t+1; R₀ = rata reproductiva neta).

Se poate constata ca multe depind de valoarea lui R₀ (daca R₀ < 1, populatia merge spre extinctie; cand R₀ = 1 - populatia ramane constanta = populatie in echilibru; cand R₀ > 1 - populatia creste) (Fig. 5-24).

Un model de crestere de tip exponential caracterizeaza de exemplu bacteriile si protozoarele. Dar aceasta nu poate decurge la infinit, existand si o rata mare a mortalitatii. Daca nu ar fi asa, celulele de bacterii se pot divide tot la 20 minute, astfel ca in x ore ar atinge un numar de 2^3x celule. Admitand ca volumul unei bacterii este de 1μ³ in 43 ore s-ar atinge volumul Terrei !.

Examinarea taxei mortalitatii in faza exponentiala de crestere se poate face prin liniarizarea ecuatiei cresterii exponentiale:

prin logaritmare:

ln N = ln N₀ + r t

log₁₀ N = log₁₀ N₀ + 0,4343 r t

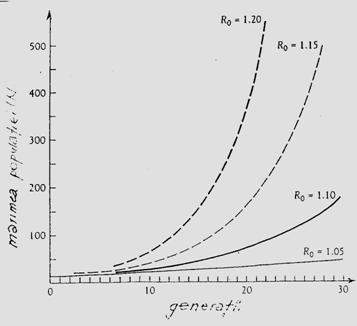
Fig. 5-24. Exemple de crestere exponentiala (geometrica) a populatiei. Generatii distincte, rata reproductiva constanta. N₀ = 10 (dupa Stiling, 1996).

Logaritmarea ordonatei permite liniarizarea iar forma curbei exponentiale astfel obtinuta este ilustrata in Fig. 5-2

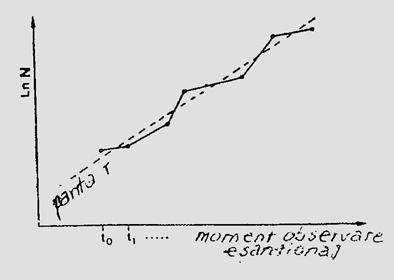
Fig. 5-2 Determinarea directa a ratei de crestere r (panta unei drepte) dupa liniarizarea functiei exponentiale de crestere (dupa Frontier si Pichod-Vial, 1998).

4.4.3. Cresterea logistica (a lui Verhulst)

Cand curba de crestere la multe populatii este lenta - in relatia marimea populatiei si timp - , curba care se obtine are forma literei "S" si reprezinta cresterea sigmoida (logistica ) (Fig. 5-27, b).

Interpretarea simplista este urmatoarea: in prima faza cresterea este activa, de tip exponential; apoi se atenueaza si are loc dupa un model liniar; partea terminala arata o stabilizare, cresterea este de tip logaritmic si arata ca oricat ar creste timpul, populatia nu mai creste sau creste foarte putin.

In ecuatia logistica rata de crestere a populatiei este data de relatia:

Se observa ca relatia este aceeasi ca si cea din cazul cresterii exponentiale cu exceptia termenului:

(= rezistenta mediului)

(K = capacitatea de sustinere = de suportare a mediului)

Cand N este mic [(K-N) / K] este 1; cand rezistenta mediului este mica valoarea numerica a relatiei [(K-N) / K] = 1; cand rezistenta mediului este mare, valoarea numerica a relatiei [(K-N) / K] se apropie de 0. In aceasta situtie, potentialul biotic este aproape complet realizat si cresterea populatiei este rapida. Sa presupunem ca N = 1; K = 50. Atunci cand N = 5:

La limita superioara a curbei unde aceasta are o portiune dreapta, se gaseste capacitatea portanta = capacitate de suportare a mediului = capacitate de sustinere a mediului (carrying capacity) (K), care poate fi interpretata in 4 moduri diferite si reprezinta:

- limita impusa de abilitatea mediului de a suporta populatia la un nivel de supravietuire redus; nu exista suficienta hrana pentru o crestere optima a corpului, vigoarea si sanatatea populatiei; orice schimbare, cat de mica, de la aceasta stare poate duce la catastrofe (Dasmann, 1964);

- densitatea optima la care populatia are hrana si alte conditii adecvate; indivizii se apropie de maxim in greutatea corpului, vigoare si sanatate; populatia ramane insa putin timp la acest nivel deoarece apar daunatori iar populatia este controlata de teritorialitate sau de natalitate;

- un prag de securitate; daca densitatea unei populatii este deasupra unui anumit nivel exista o instabilitate in populatie (o parte din indivizi pot pleca din populatie iar altii pot fi afectati de pradatori); in acest caz, densitatea de securitate este corespunzatoare unei densitati tolerante, or unei densitati optime (Errington, 1946);

- densitate toleranta; este o densitate de saturatie (numarul sau biomasa de organisme pe care le poate suporta un anumit habitat) (Odum, 1993).

Aplicarea acestui concept, la diferite nivele de organizare ierarhica in ecologie (populatie, biocenoza, ecosistem) este totusi foarte dificila. Se pune des intrebarea care poate fi limita superioara a lui K in conditiile cresterii unei populatii care poate fi sustinuta de un mediu de viata dat ?. Specialistii iau in considerare existenta a doua nivele: (a) un maxim sau o densistate de subzistenta sau un maxim al numarului de indivizi care poate sa-si prelungasca existenta in habitat; (b) un nivel optim sau "sigur" la o densitate mai mica si la care exista o mai mare siguranta pentru indivizi, in ceea ce priveste hrana, rezistenta la pradatori sau fluctuatia periodica a resurselor (Odum, 1993). Daca urmarim curba cresterii logistice, unde este marcat K ca reprezentand nivelul maxim, un nivel optim poate fi apreciat ca localizat intre acest maxim si un punct de inflexiune unde rata cresterii populatiei este cea mai mare iar densitatea este cam jumatate sau 2/3 ca marime.

Ca exemplu oate fi citat cazul speciilor de Cervidae (Cervus sp., Capreolus sp. etc) Astfel, populatia atinge limita K, in absenta pradatorilor, printr-o inmultire rapida; rezultatul acestei cresteri este un pasunat excesiv iar vegetatia nu mai poate oferi un suport de existenta ca in cazul populatiei incipiente sau anterioare. Experimental s-a trecut apoi la o mutare de exemplare sau printr-un fenomen experimental de predatorism pana la o rata care sa mentina populatia la un nivel optim. Pe baza unor studii de durata s-a evidentiat ca valoarea pentru K maxim este de 90 indivizi/mila², iar K optim de 50 indivizi/mila² (Mc Cullough, 1979).

Aceste principii sau concepte sunt valabile atat pentru populatiile de animale cat si pentru cele de plante. Astfel, in cazul unor specii de plante (ex. Pinus sp.) un numar de 100 exemplare au crescut relativ bine impreuna pe un lot experimental. Cu timpul insa, cresterea s-a incetinit si a crescut mortalitatea. Reducerea densitatii la a modificat radical situatia; a crescut calitatea si fiecare individ a prezentat o valoare economica mare.

In impactul lor cu mediul insa, reactia indivizilor se poate inscrie pe un spectru larg. Fenomenul este cu atat mai vizibil si interesant referitor la populatia umana. In azul acesteia, pe langa resursele ca de suport de viata mai intervine un al doilea parametru - intensitatea de folosinta. In acest caz, capacitatea de suportare a mediului (K), in cazul populatiei umane, a fost definita ca volumul si intensitatea de folosinta a resurselor (Catton, 1987) (autorul sugereaza chiar legarea conceptului K de Legea minimului lui Liebig, pentru estimarea limitelor superioare).

Atentie. Este important de retinut ca in ceea ce priveste capacitatea de suportare a mediului (K), aceasta nu este o constanta (precum este K din ecuatia de crestere), iar pentru populatia umana ea nu este infinita.

In cazul ecosistemelor naturale, la nivel global, capacitatea de suportare a mediului (K) ar putea fi aproape de o constanta, atat timp cat nivelul si calitatea energiei solare (input) ramane constanta.

Cele 2 relatii importante ale cresterii populatiilor sunt:

a. pentru cresterea exponentiala: (1)

b. pentru cresterea logistica (ecuata lui Verhulst): (2)

Formele diferentiale ale acestor ecuatii pot fi prezentate in urmatoarea forma:

(1): rata de crestere = rata reproductiva r ∙ numar N

(2): rata de crestere = rata reproductiva r ∙ numar N ∙ factorul propriu de limitare (rezistenta mediului)- [(K-N)/K]

Cele doua constante importante sunt: K - nivelul capacitatii superioare de suportare a mediului si r - rata intrinseca de crestere a populatiei intr-un mediu nelimitat.

r-K selection. In medii de viata in care nu exista o aglomerare de indivizi ai vreunei specii (ex. cazul colonizarii unui agroecosistem dupa ce o anume cultura a fost abandonata, popularea incipienta a unor noi medii de viata etc), presiunea selectiei naturale va favoriza intotdeauna speciile cu un potential mare al ratei reproductive, deci cu un numar mare de urmasi. Opus, in medii aglomerate (ex. o padure matura si stabila) selectia naturala va favoriza speciile cu rata redusa de crestere, dar adaptate bine la aceste conditii si capabile sa utilizeze cu eficienta maxima resursele disponibile. Ceeea ce am prezentat succint aici este cunoscutul principiu al selectiei r-K (r-K selection), situatii in care speciile manifesta o strategie r ("generalisti") sau o strategie K ("specialisti") (Odum, 1993; Rejmanek si Spitzer, 1980; Spitzer si Rejmanek, 1982)

4.4.4. Relatia dintre cresterea populatiei si densitate

Un prim caz este acela in care, cu cat densitatea creste, rata cresterii descreste. Este tipul de relatie invers dependenta de densitate (Fig. 5-26, c).

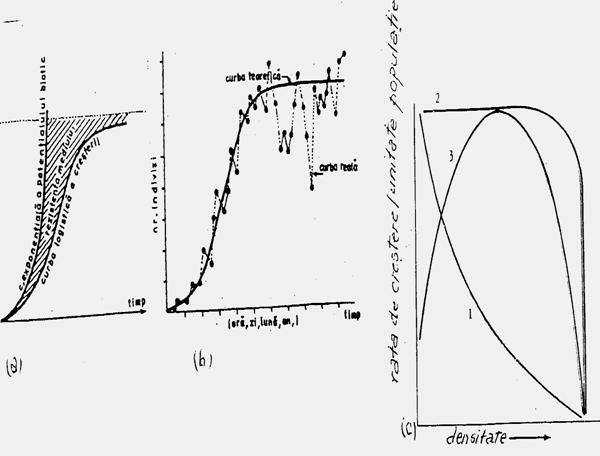
Fig. 5-26. (a). Reprezentarea schematica a modelului curbei logistice de crestere si a curbei exponentiale a potentialului biotic. (b). Curba logistica, teoretica si reala (dupa Stan, 1994 (1995). (c). Trei modele ale cresterii populatiei in relatie cu densitatea (curba 1 = tipul de relatie invers dependenta de densitate; curba 2 = tipul independent de densitate; curba 3 - tipul Allee (dupa Odum, 1993).

O alta situatie este aceea cand rata cresterii ramane la nivel ridicat pana ce densitatea va creste de asemenea la un nivel mare si apar alti factori externi limitativi. Cand exista o serie de factori externi a caror actiune este relativ slaba (ex. pradatori, lipsa de hrana sau hrana putina, factori fizici ai mediului etc), aceste specii pot suferii oscilatii pronuntate ale densitatii si cresterii, cu efecte imprevizibile sau negative asupra factorului uman. Este cazul speciilor care in literatura de specialitate sunt considerate "daunatoare". Unele pot fi daunatori permanenti datorita unui nivel constant mare al populatiilor. Sunt daunatori tipici, mai ales in cazul acelor specii unde planta gazda este o planta cultivata. Alte specii au densitati relativ constant-reduse dar sunt tot daunatoare (ex. lepidopterul Mamestra brassicae). Un alt caz este acela al unor specii cu nivel constant mare al populatiilor dar nu produc daune decat cu totul intamplator, dar cand densitatea creste exploziv pot fi daunatori ocazionali. Este cazul multor specii extrem polifage (ex. Xestia c-nigrum) Acesta este tipul independent de densitate (Fig. 5-26, c; curba 2).

In cazul speciilor de animale sociale sau plante coloniale, rata cresterii atinge nivelul cel mai mare la o densitate intermediara. Atat densitatea mica cat si cea mare determina o scadere a ratei de crestere. Este asa numita forma de crestere a lui Allee (Allee, 1951) (Fig. 5-26, c; curba 3).

Mai este cunoscut cazul speciilor caracterizate de explozii populationale (dupa terminologia "boom and bust"). Adica, are loc o crestere exploziva, cu atingerea unei densitati mari, dupa care se constata o revenire la normal printr-o scadere a nivelului populatiilor, la fel de pronuntata (ex. ciclul de 4 ani al lemingilor, unele specii de insecte - gandacii de scoarta, lacustele etc).

Curba logistica ilustrata (Fig. 5-26, b) este o curba teoretica. Curba dupa care are loc relatia dintre numarul de indivizi si timp are in realitate un trend ferestruit. Aceasta este curba reala. Intervalul (spatiul) dintre curba exponentiala a potentialului biotic si curba logistica reprezinta rezistenta mediului (Fig. 5-26).

Am aratat ca o alta forma a relatiei cresterii logistice poate fi scrisa sub forma ecuatiei lui Verhulst:

de unde:

Prin liniarizarea acestei forme obtinem:

Aceasta este ecuatia unei drepte pentru r si care trece prin origine (Fig. 5-27).

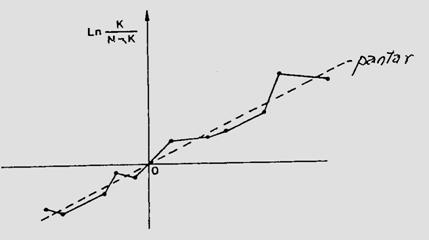
Fig. 5-27. Liniarizarea curbei logistice si determinarea directa a ratei de crestere r (dupa Frontier si Pichod-Vial, 1998).

Cresterea populatiei umane. Populatia umana a cunoscut si modele extreme de crestere. Un model de crestere negativa a fost inregistrat prin sec. XIV, cand ciuma bubonica ("moartea neagra") a redus populatia Europei cu 25% (Freedman si Berelson, 1974). In anumite secole, populatia umana a crescut incet, comparativ cu altele. Perioadele de crestere accentuata si rapida au fost legate de procurarea resurselor de energie:

- prima crestere pronuntata a fost dependenta de dezvoltarea agriculturii (ceea ce a determinat si o crestere a capacitatii de suportare a mediului, fiind realizata acum circa 8000 de ani);

- a doua a fost asociata de revolutia industriala (acum circa 200 ani; ceea ce a determinat o colonizare sustinuta si accentuata a continentelor, descresterea mortalitatii si cresterea numarului de membrii prin cresterea ratei natalitatii si prelungirea duratei de viata ca rezultat al progreselor din medicina si sanatate) (procentajul de crestere al populatiei umane a fost de 80%, numai in ultimele 2 secole; azi atinge 5-6 miliarde locuitori/Terra; demografi cu experienta sustin ca in aceste conditii ale unei cresteri logistice, in urmatorul secol, populatia va fi de 9-14 miliarde locuitori !).

O modalitate sugerata de specialisti pentru a descrie cresterea populatiei umane este termenul de dublarea timpului (= numarul de ani necesari pentru dublarea densitatii). Cresterea anuala este exprimata in numarul de persoane adagate la o suta existenta (sau exprimata procentual) (ex. o crestere de 2 procente annual inseamna 2 persoane la 100, respectiv 200 la 1000 deja existente). Pentru estimarea aproximativa a dublarii timpului t, pentru o rata de crestere r de 2% (exprimata in fractie zecimala), exista urmatoarea relatie:

Un procent de 2% nu pare a fi prea mult, dar la aceasta rata inseamna ca populatia orasului Cluj, creste de 2 ori pe durata de viata a unei persoane (la ora actuala, pe Terra, rata de crestere este de 1,8%; in unele tari subdezvoltate este de 3% ceea ce inseamna ca timpul de dublare va fi peste 23 de ani !; in tarile dezvoltate si supradezvoltate, rata este <1% iar dublarea timpului va fi peste 70 ani sau mai mult; la polul opus sunt unele tari unde rata este in jur de 0% !). La nivel mondial, rata de crestere este cuprinsa intre una joasa (o medie in jur de 0,8%) si una mare (media de 2,5%) (Brown si Jacobson, 1986).

Legat de cresterea populatiei umane sunt o serie de pareri contraversate. Unii sociologi, economisti si ecologi sustin fenomenul de tranzitie demografica (pornind de la ideea ca populatia umana va incetini ritmul de crestere ca popor fiind in viitor mai putin dependenta de copii lor; va creste tendinta de a avea putini copii si a folosi resursele pentru cresterea calitatii vietii - adica a trecere spre un stil de viata de forma K). Din acest punct de vedere, cresterea populatiei este o problema de economie (McNamara, 1982). Se para insa ca lucrurile sunt mult mai complicate, fiind importante nu numai aspectele economice dar si cele de dezvoltare calitativa, de constiinta si educatie, de controlul natalitatii etc (Brown si Johnson, 1986).

4.4. Cresterea Von Bertalanffy (ecuatia von Bertalanffy; ecuatia Ivlev)

Este o ecutie folosita in cazul cresterii individuale si in particular in cazul cresterii in lungime. In acest caz, din curba logistica se ia in considerare doar portiunea dreapta (exponentiala negativa). Aceasta este de forma:

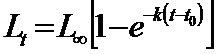
(L_t = lungimea la timpul t; L_∞ = talia limita posibila; k (>0) = coeficient instantaneu de crestere; t₀ = data nasterii fictive unde talia ar fi 0 (ceea ce practic nu este posibil; astfel curba initiala nu ar fi de tip logistic cu trecere prin origine ci deplasat fata de aceasta - Fig. 5-28, a).

Ecuatia de mai sus arata ca diferenta intre talia atinsa si talia limita, tinde spre 0 exponential si se poate scrie:

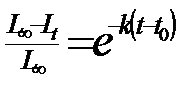
Este o cuba realista folosita frecvent in ecologie dar care neglijeaza aspectul cresterii juvenile astfel ca partea incipienta a curbei poate fi neglijata.

Se observa ca aceasta ecuatie descrie o curba care imita curba exponentiala de crestere. Din ultima relatie, prin derivare in functie de timp se deduce diferentiala de forma:

de unde,

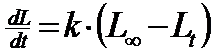
Ca si in cazul celor doua tipuri de crestere prezentate anterior, si in acest caz, prin liniarizare (cu logaritmarea ordonatei) din forma doua a ecuatiei lui Von Bertalanffy se deduce:

care este ecuatia unei drepte cu panta de inclinatie k (Fig. 5-28, b).

Fig. 5-28. Ilustrarea curbei de crestere Von Bertalanffy, in forma sa exponentiala (a) si dupa liniarizare (b) (dupa Frontier si Pichod-Vial, 1998).

4.4.6. Cresterea Gompertz (ecuatia Gompertz)

Reprezinta o curba de forma celei logistice doar ca este disimetrica. In partea sa initiala prezina o crestere de tip exponential pozitiv, de durata insa foarte scurta comparativ cu restul. Punctul de inflexiune este atins la un nivel inferior care reprezinta jumatatea nivelului limita maxima (Fig. 5-29, a).

Concluzie. Am prezentat succint 4 modele pentru studiul cresterii populatiei cat si pentru studiul cresterii indivizilor din populatie. Toate au puncte comune. Astfel, cresterea exponentiala pozitiva descrie debutul unui proces de crestere (inainte de a aparea anumite limitari). Cresterea logistica se refera la realitatea intregului proces de crestere, pe toata durata de timp. Modelul Von Bertalanffy descrie sfarsitul unui proces de crestere, atunci cand talia se apropie de valoarea limita ( este "opus" celui exponential). Modelul logistic al lui Gompertz descrie ansamblul cresterii (similar functiei logistice), dar introduce o disimetri prin cele doua componente: prima parte a procesului de crestere este mai scurta decat cea de a doua.

Trendul curbelor celor 4 modele este ilustrat in Fig. 5-29, e)

Cand, cum si ce tip de model se alege ?. Mai intai este necesar ca cercetatorul sa dispuna de observatii (cel putin preliminare) asupra indivizilor si populatiei respective. Cand se trece la lucru in camp (prelevare de probe) este necesar a sti in ce stadiu se afla populatia (la inceput, la mijloc sau la sfarsitul procesului de crestere). Daca nu se dispune de aceste date se face un studiu preliminar prin care se analizeaza variatia vitezei de crestere in functie de talia organimului

Fig. 5-29. (a) - Tip de curba de crestere dupa modelul ecuatiei lui Gompertz. (b) - Modelul curbei Von Bertalanffy dupa aplicarea logaritmarii. (c) - Curba normala de crestere Gompertz. (d) - Determinarea grafica a parametrilor A si B a modelului Gompertz, prin linearizare dupa metoda Baranowitz. (e) - ilustrarea schematica a trendului celor 4 tipuri de cutbe de crestere analizate dupa Frontier si Pichod-Vial, 1998).

4. Tendinta de evolutie a populatiei in timp

Prin metodologie matematica se poate analiza complex populatia unei specii, evolutia abundentei, pe baza unui plan de esantionare sistematic, in cadrul unui monitoring sistematic si de durata. Datele obtinute pot evidentia nu numai starea actuala a populatiilor, dar prin compararea rezultatelor din prezent cu cele din anii trecuti se poate obtine o curba al carei trend arata tendinta pe care o are populatia si se poate deci prognoza evolutia ei in viitor (Fig. 5-30). Modelul obtinut este ilustrat de o dreapta de regresie, pe baza analizei datelor cu ajutorul ecuatiei regresiei liniare simple. Aceasta este tendinta centrala si ea este deci un caz particular al regresiei simple (vezi exercitiul din continuare). Se refera deci la fenomene care se desfasoara in timp.

Se iau in considerare cele doua variabile (x = variabila independenta = timpul (anul); y = variabila dependenta = marimea populatiei locale). Prin aceasta modalitate se pot studia diferite aspecte cum sunt: - dinamica populatiei de insete dintr-un biotop

- dinamica, capturarii ♂ unei specii intr-o capcana (capcana luminoasa, feromonala, alimentara, Barber etc);

- dinamica biomasei noctuidelor in zona . pe baza datelor de la capcana luminoasa.

- evolutia marimii numerice a populatiilor speciei X in zona.. pe durata a 10 ani.

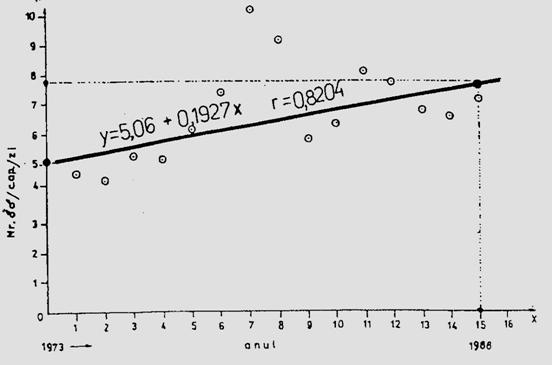
Fig. 5-30. Tendinta de evolutie a populatiei in timp. Model sugerat cu ajutorul ecuatiei si dreptei de regresie dupa datele din text (dupa Stan, 1993).

4.6. Factori cu actiune asupra dinamicii populatiilor

Toate populatiile sunt afectate de schimbarile din mediu. Uneori cauzele sunt de alta natura. Din acest punct de vedere, orice populatie si mediul sau sunt considerate un sistem complex de interactiuni. Trebuie insa aratat ca exista multe puncte de vedere divergente an ceea ce priveste punctele de vedere ale ecologistilor referitor la ponderea semnificatiei a fiecarei componente a acestui sistem. Schimbari drastice si imprevizibile ale mediului pot determina o mortalitate masiva. Pe de alta parte, boli sau daunatori pot decima populatiile. In alte situatii starile de stress datorate unei suprapopulari pot induce un comportament agresiv care duce la mortalitate masiva. La polul opus sunt conditiile favorabile (factori climatici, hrana, potentialul reproductiv etc) care determina cresterea nivelului populatiei.

Cresterea numerica a unei populatii nu este infinita. Ea atinge niste valori maxime, dupa care revine la un nivel minim, de fiecare data osciland in jurul unei valori medii. Date practice sugereaza astfel ca exista o serie de factori care determina aceste oscilatii si mecanisme care regleaza variatiile acestea numerice intre anumite limite specifice. Ca urmare a acestor actiuni se restabilesc efectivele populatiilor induse in urma perturbarilor. Diversitatea fenomenului ecologic face dificil un studiu izolat sau o concluzie trasa in afara intregului. Aspectele calitative sunt imbinate cu cele cantitative

Influenta factorilor externi sau interni nu se rezuma numai la actiuni directe asupra nivelului populatiei influentand natalitatea sau mortalitate si si sub alte aspecte (frecventa indivizilor inainte si dupa reproducere, rata sexelor, starea de sanatate etc). Factorii care influenteaza dinamica populatiilor sunt asfel diversi. Unii autori ii impart in doua categorii mari: factori dependenti de densitatea populatiei si factori independenti de densitatea populatiei (Lack, 1954; Stugren, 1975).

Daca am lua in considerare o categorie de specii animale unde abundenta si respectiv dinamica sunt influentate de factori dependenti de densitate, s-ar impune studii laborioase pentru a dovedi aceasta.

Este adevarat ca populatiile multor specii sunt afectate de o serie de factori care sunt direct dependenti de densitatea populatiei respective. Este cazul populatiilor supraaglomerate unde si mortalitatea este mare, fie datorita aparitiei epidemiilor, fie datorita modelului comportamental agresiv sau dominant. Cu cat densitatea este mai mare cu atit mortalitatea in acest caz va fi mai mare. Astfel, actiunea acestor factori nu este in functie de timp ci de marimea populatiei, regland nivelul acesteia la o densitate relativ medie optima dupa o crstere anterioara excesiva. In aceasta categorie se inscriu exemplu de decimarea unor populatii depasari in urma unor epidemii (cazul de acum al pestei aviare, al gripei aviare). Cercetari efectuate la specii de rozatoare au evidentiat ca la aceste populatii o parte dintre animale sunt in permanenta infestate cu agenti patogeni. Aparitia si raspandirea epidemiei nu este legata strict de densitate ci apare ca un fenomen ciclic, natural in orice biocenoza care constituie focar de infectie. Periodicitatea epidemiilor depinde de o serie de factori, cum sunt: oscilatiile periodice al nivelului populatiilor, fluctuatiile nivelului populatiei de microorganisme patogene, nivelul populatiilor agentului patogen la gazdele intermediare asociat cu evolutia densitatii acestora, nivelul de sensibilitate a speciei gazda la agentul patogen.

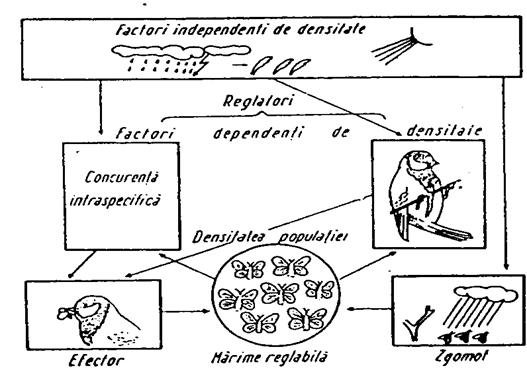
Fig. 5-31. Mecanismul cibernetic pe principiul feedback al reglarii dinamicii populatiilor (dupa Wilbert, 1962; modif. Stugren, 1975).

Realitatea este insa alta. In natura factorii actioneaza simultan. In cazul agentilor patogeni este importanta capacitatea populatiei speciei gazda de a reactiona la actiunea oricarui factor. Nici o populatie a unui agent patogen nu a decimat in totalitate o populatie. Chiar daca exista o specie de prada caracterizata de abundenta mare, nu duce neaparat la decimarea gazdei. In natura acest lucru nu se intampla (in cap. urmator, in cadrul relatiei prada - pradator vom vedea ca modelul de evolutie este cu totul altul, curbele de dezvoltare avand un trend similar, dar decalat in timp). Bazat pe aceste considerente sunt autori care neaga corectitudinea clasificarii factorilor care regleaza dinamica populatiilor, in cele doua categorii (Andrewartha si Birch, 1954; Viktorov, 1960).

Daca am face referire la factori care sunt independenti de densitate, aici ar intra toti cei a caror actiune este corelata cu durata de timp cat actioneaza (Stugren, 1975). Deci acesti factori determina efectul respectiv, indiferent daca densitatea populatiei este mare sau mica. In aceasta categorie intra practic toti ceilalti factori ecologici, analizati la nivelul de organizare individual.

Sistemul cibernetic al reglarii dinamicii populatiilor. Toti factorii implicati in reglarea nivelului populatiilor isi manifesta actiunea intr-un sistem complex, integrat. Principiul feedback este caracteristic in mecanismul acesta al reglarii densitatii (Fig. 5-31).