| CATEGORII DOCUMENTE | ||
|
||
| Demografie | Ecologie mediu | Geologie | Hidrologie | Meteorologie |
ASPECTE FUNDAMENTALE IN DINAMICA STRUCTURILOR
Relatia Actiune - Sistem - Raspuns
Actiuni dinamice
In Statica constructiilor se determina raspunsul structurii la actiuni cu valori precizate. Rezulta diagrame de eforturi de tip M, T si N. In Dinamica constructiilor, actiunile sunt functii de timp si diagramele de eforturi sectionale rezulta de forma M(t), T(t) si N(t).
Deplasarile
structurilor vor fi de asemenea functii de timp 
si vor fi insotite de forte de inertie 
(m
reprezinta masa). Daca fortele de inertie sunt neglijabile in raport cu
celelalte forte atunci de poate considera ca actiunile nu mai sunt dinamice ci
actiuni statice variabile in timp.
Clasificarea actiunilor dinamice:
Dupa natura lor:
o Actiuni naturale, independente activitatilor umane, provin in general din miscarile seismice, presiunile vantului in rafale, etc.
o Actiuni artificiale, proprii activitatilor umane, provin din procesele tehnologice industriale, din trafic (rutier, feroviar), din explozii, etc.
Dupa modul de transmitere:
o Actiuni directe, se aplica direct asupra elementelor portante ale sistemului structural.
o Actiuni indirecte, sunt acele actiuni care se transmit structurilor prin diverse medii de propagare (explozii subterane, actiuni seismice).
Dupa reprezentarea matematica:
o Actiuni deterministe, se caracterizeaza printr-o variatie complet definita in timp.
o Actiuni aleatoare, (intamplatoare, cauzale sau ramdom) sunt acele actiuni a caror variatie nu este pe deplin definita in timp si care poate fi caracterizate numai pe baze statistice.
Dupa durata:
o Actiuni permanente, se exercita un timp indelungat asupra sistemului structural.
o Actiuni tranzitorii, sunt actiuni de durata scurta, impulsive (socuri produse de echipamente si agragate industriale, vant in rafale, actiuni seismice bruste, explozii).
Sistem dinamic
In Statica constructiilor sistemul dinamic are o singura caracteristica si anume: caracteristica de deformabilitate (d = flexibilitate sau r = rigiditate). Mai general, sistemul este caracterizat de matricea de flexibilitate [d] sau de matricea de rigiditate [r].
In Dinamica structurilor sistemul are 3 caracteristici:
Raspunsul dinamic
In general raspunsul dinamic se exprima prin marimi cinematice fundamentale, adica prin: acceleratii, viteze si deplasari instantanee, pe baza carora se calculeaza orice alta marime rezultanta. Aceste marimi pot fi: eforturile sectionale M, T si N, deformatiile specifice, energia de deformatie, energia cinetica, etc.
Modelarea sistemului dinamic
Descrierea analitica a comportarii unui sistem dinamic se exprima pe baza unui model matematic. Modelul matematic devine identic cu modelul dinamic atunci cand toate carcateristicile de definire ale sistemului dinamic sunt complet precizate din punct de vedere fizic.
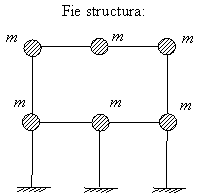
Modelare inertiala. Coordonate dinamice
Pozitia unui sistem dinamic, in orice moment al miscarii va fi determinata printr-o infinitate de parametri independenti sau coordonate dinamice, numite si grade de libertate dinamice (GLD). In vederea simplificarii operatiilor numerice, orice structura poate fi transformata intr-un sistem dinamic cu mase discrete, prin modelarea corespunzatoare a celui cu masa distribuita.
Coordonatele dinamice independente care pot defini complet pozitia instantanee a unui sistem dinamic discret, in orice moment al miscarii, se numesc grade de libertate dinamice (GLD). Deplasarile pe directia coordonatelor dinamice reprezinta necunoscutele fundamentale in dinamica structurilor. Rezulta deci ca numarul necunoscutelor dinamice este egal cu numarul minim de legaturi simple (blocaje) necesare pentru a fixa sistemul dinamic in pozitie de repaus. Un exemplu elementar de discretizare a unei structuri plane este prezentat in figura anterioara. Prin fragmentarea acesteia se obtine concentrarea maselor, structura avand doar rol de suport elastic.
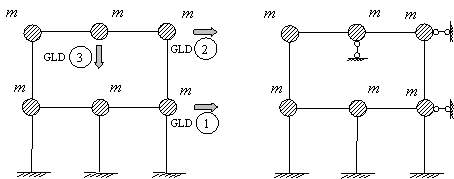
In vederea simplificarii operatiilor de analiza numerica, matricea maselor poate fi diagonalizata prin unele procedee specifice. Diagonalizarea matricei maselor corespunde unui decuplaj inertial cand toti coeficientii secundari devin zero, adica mjk=0, iar mjj=mj (j=1..n).
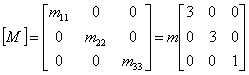
Modelare disipativa. amortizare interna
Disiparea energiei induse in sistemele dinamice, de surse perturbatoare exterioare, depinde in general de mai multi factori dintre care pot fi considerati definitorii urmatorii: capacitatea de amortizare interna a materialului, tipul sistemului structural, conxiunile dintre elementele de rezistenta componenete si conexiunile cu mediul de fixare.
In analiza dinamica a sistemelor liniare, disiparea de energie este subtituita de fortele rezistente, care se opun miscarii. Forma de amortizare considerata in acest curs este cea de tip vascos, model ce genereaza forte proportionale cu viteza instantanee a sistemului. In domeniul liniar de comportare se va considera un coeficient de proportionalitate c a carui valoare nu se modifica pe durata miscarii libere sau fortate a sistemului dinamic.
In rezolvarile
practice este mai sugestiv sa se foloseasca notiunea de fractiune din
amortizarea critica, notata cu ν,
care se exprima prin raportul adimensional dintre coeficientul efectiv de
amortizare vascoasa c si coeficientul
de amortizare critica ccr,
adica 
.
Coeficientul de amortizare critica reprezinta o cantitate limitata de
amortizare vascoasa care elimina complet vibratia sistemului, conducand la o
vibratie aperiodica. Pentru structurile reale, capacitatea naturala de
amortizare vascoasa este destul de redusa, conducand la valori ale fractiunii
din amortizarea critica cuprinse in intervalul 
.
In cazul sistemelor dinamice cu n GLD, expresia matricei de amortizare vascoasa, exprimate in coordonate dinamice are forma:
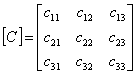
unde coeficientii
de tipul 
reprezinta forta de amortizare generalizata
care se manifesta pe directia coordonatei j,
datorita unei viteze generalizate unitare imprimata pe directia coordonatei k.
In baza teoremei de
reciprocitate Maxwell-Betti, rezulta ca 
si deci matricea de amortizare vascoasa este
simetrica, adica: 
.
Coeficientii
secundari de tipul pun in evidenta existenta unui cuplaj
disipativ. Problema decuplarii disipative, implicit a diagonalizarii matricei
de amortizare, se pune in aceeasi maniera ca in cazul decuplarii inertiale.
In conformitate cu modelul propus de Rayleigh, forma generala a matricei de amortizare vascoasa, exprimata prin caracteristicile inertiale si elastice ale sistemului cu n GLD, are forma:
unde 
si 
sunt constante de proportionalitate, 
reprezinta matricea de inertie, iar 
reprezinta matricea de rigiditate a sistemului
exprimata in coordonate dinamice.
Modelare elstica. flexibilitate - rigiditate
Modelarea elastica a sistemelor dinamice se refera la evaluarea proprietatilor de flexibilitate si de rigiditate in raport cu coordonatele dinamice. Aceste proprietati fundamentale atat in statica constructiilor cat si in dinamica structurilor caracterizeaza deformabilitatea sistemelor.
In Dinamica structurilor coeficientii de rigiditate si de flexibilitate se definesc in raport cu coordonatele dinamice (GLD) ale sistemului.
Coeficientii de flexibilitate se definesc, in general, ca fiind efecte generalizate produse de cauze generalizate egale cu unitatea. Atat efectele cat si cauzele se manifesta pe directiile GLD. Pentru sistemul dinamic prezentat anterior matricea de flexibilitate dinamica va avea forma:
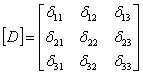
unde 
reprezinta deplasarea generalizata pe directia
coordonatei j, cand pe directia
coordonatei k actioneaza o forta
generalizata egala cu unitatea. Intrucat 
rezulata ca matricea 
este o matrice simetrica si se poate scrie
relatia: 
.
Coeficientii de rigiditate, prin definitie reprezinta cauze generalizate care produc efecte generalizate egale cu unitatea pe directia coordonatelor dinamice ale sistemului (GLD). Forma generala a matricei de rigiditate pentru un sistemul dinamic prezentat este:
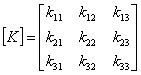
unde 
reprezinta forta generalizata aplicata pe
directia coordonatei j astfel incat sa produca pe directia coordonatei
generalizate k o deplasare generalizata egala cu unitatea, iar pe directia
celorlalte coordonate deplasari nule. Matricea de rigiditate este simetrica si
se poate scrie relatia: 
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |
Vizualizari: 2505
Importanta: 
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved
