DINAMICA SISTEMELOR CU 1 GLD. VIBRATII FORTATE NEAMORTIZATE PRODUSE DE ACTIUNILE ARMONICE

Dinamica sistemelor cu 1 GLD. Vibratii fortate neamortizate produse de actiunile armonice

In ecuatia de echilibru dinamic instantaneu care va caracteriza miscarea sistemului, intervin urmatoarele forte: (i) forta de inertie, ; (ii) forta elastica, si (iii) forta perturbatoare . In continuare se va considera armonica avand forma .

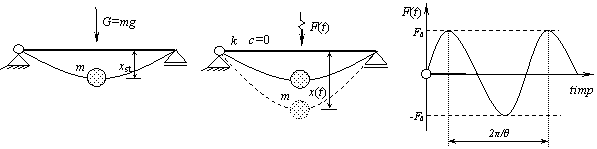
Ecuatia de miscare a sistemului dinamic rezulta de forma:

Solutia acestei ecuatii diferentiale de ordinul II cu coeficienti constanti este de forma unde:

reprezinta solutia ecuatiei omogene, care corespunde vibratiilor libere fara amortizare si care are forma ;

• reprezinta solutia particulara, care corespunde perturbatiei armonice si reprezinta raspunsul sistemului la excitatia si care este de forma .

Constantele M si N se determina din conditia ca aceasta solutie sa satisfaca ecuatia miscarii:

Prin identificarea coeficientilor functiilor trigonometrice rezulta:

si

Solutia particulara devine: , iar solutia generala va avea forma:

Ecuatia vitezei se obtine prin derivarea expresiei anterioare:

Constantele de integrare se determina din conditiile initiale: si . Introducand aceste conditii in ultimele doua relatii vom obtine:

si

Daca forta perturbatoare incepe sa actioneze asupra sistemului dinamic cand acesta se afla in repaus, adica daca la si , rezulta ca:

Factorul dimensional al expresiei anterioare va fi transformat cu scopul de a pune in evidenta semnificatia sa.

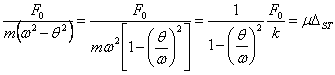
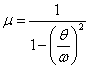
reprezinta factorul de amplificare dinamica, iar reprezinta deplasarea statica pe directia GLD produsa de actiunea statica a fortei (aplicata sistemului pe directia de actiune a fortei perturbatoare).

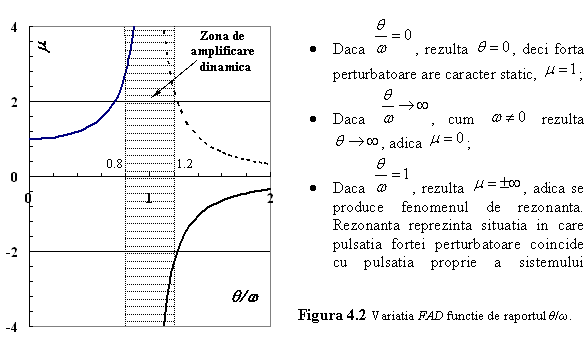
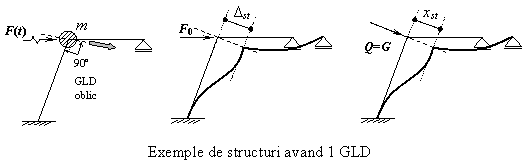
Cu aceste notatii expresia generala a raspunsului fortat exprimat in deplasari dinamice rezulta:

iar raspunsul stationar (permanent):

Expresia caracterizeaza un factor de amplificare dinamic variabil in timp.