CURBE PE SUPRAFETA ELIPSOIDULUI DE REFERINTA

CURBE PE SUPRAFETA ELIPSOIDULUI DE REFERINTA

1. Sectiuni normale principale

Planul normal este planul ce contine normala la suprafata elipsoidului intr-un punct ( in cazul nostru S). Sectiunea normala este intersectia dintre planul normal si suprafata elipsoidului. Pentru un punct dat putem avea o infinitate de sectiuni normale. Dintre acestea, interes in geodezie il prezinta numai doua si anume: sectiunile cu raza maxima de curbura, respectiv cu raza minima de curbura care se mai numesc si sectiuni normale principale. Sectiunea cu raza minima de curbura, notata cu M, se numeste sectiunea normala principala a elipsei meridiene sau meridiana. Ea reprezinta intersectia suprafetei elipsoidului de rotatie cu planul format de arcul de meridian al punctului si axa polilor geografici. Sectiunea cu raza maxima de curbura, notata cu N, este sectiunea normala principala a primului vertical N si se numeste marea normala si este perpendicular pe prima.

Sectiunea elipsei meridiene

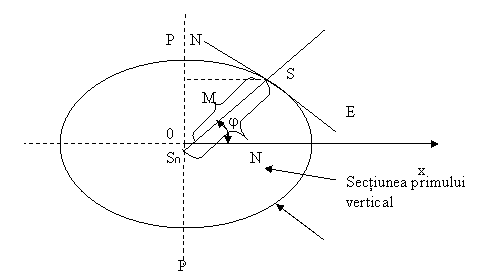
fig. nr. 1

In afara de cele doua sectiuni normale, in cadrul figuri de mai sus, pentru punctul nostru S mai este figurata si o sectiune inclinata oarecare si anume sectiunea cercului de paralel cu r = x. Intre aceasta si sectiunile normale principale (normala la suprafata elipsoidului) unghiul de inclinare este egal cu latitudinea si este perpendiculara in punctul S pe planul tangent aici la suprafata elipsoidului. Conform teoremei lui Meusnier, raza unei sectiuni inclinate oarecare care intr-un punct dat are aceeasi tangenta cu o sectiune normala este egala cu marimea proiectiei sectiuni normale (in cazul nostru sectiunea normala este sectiunea primului vertical).

1.1. Raza de curbura M a sectiunii meridiene

Consideram punctele S si S' infinit apropiate situate la aceeasi longitudine pe elipsa meridiana de raza M. Lungimea arcului de meridian dintre acestea este arcul de meridian . Pentru calculul acesteia putem scrie ca:

M =

dar, pentru suprafete infinit mici, elementul de arc, notat cu ds se poate calcula astfel:

ds² = dx² + dz²

fig. nr. 2

M² =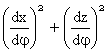

x = 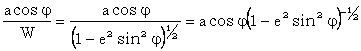; unde W =

= -

=

z =

= a

=

M² =

M =

Marimea razei de curbura depinde de latitudine si anume ea creste de la ecuator spre poli deoarece::

la ecuator avem =0⁰ ; sin = 0 M = a(1-e²)

la poli avem = 90⁰ ; sin = 1

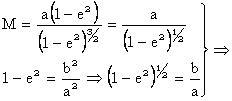M= unde c este raza de curbura polara.

Ne propunem in continuare sa exprimam pe M si in functie de parametrul auxiliar V:

M=; dar W² = V²(1-e²)

M=

In concluzie, formulele pentru calculul razei de curbura a elipsei meridiene sunt:

	M=

1. Raza de curbura N a sectiunii normale a primului vertical

In figura de mai jos se pozitioneaza punctul S pe conturul elipsei meridiene (sectiunea normala principala), se figureaza cercul de paralel al acestuia (sectiunea inclinata) si raza sectiunii normale principale a primului vertical, notata cu N ce reprezinta lungimea arcului SS₀. Conform teoremei lui Meusnier se poate calcula marimea razei sectiunii inclinate (care in cazul nostru este raza cercului de paralel al punctului S) in functie de proiectia razei sectiunii normale (sectiunea normala a primului vertical N): r = Ncosφ

fig. nr. 3

r = x =

N =

r = x = SS₀cos NcosN=

Din studiul formulei r = se observa ca r₀ la ecuator (pentru φ = 0º) este egal cu a (raza cercului ecuatorial sau semiaxa mare a elipsoidului, iar la poli (pentru φ = 90º) este nul.

Ne propunem sa comparam valorile celor doua raze de curbura ale sectiunilor principale si pentru aceasta studiem raportul

dar V =

Acest rezultat reprezinta motivul pentru care sectiunea normala a primului vertical se mai numeste si marea normala.

Daca ne propunem sa studiem valorile minime ti maxime ale valorilor acestei raze, obtinem:

la ecuator pentru = 0⁰, N₀ = a = r

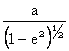a poli pentru =90⁰, === c= M.

Raza de curbura a primului vertical descreste de la ecuator la poli unde este egal cu raza de curbura a elipsei meridiene. Valorile acestor raze depind de parametrii elipsoidului si de valoarea latitudini . Pentru facilitarea calculelor in geodezie si proiectii cartografice s-au intocmit tabele ale elipsoizilor in care atat razele de curbura ale celor doua sectiuni normale principale, M si N, cat si alte elemente se gasesc calculate functie de valoarea latitudinii. Pentru elipsoidul Krasowski s-au intocmit tabelele Tarczy-Hornoch-Hristov.

O reprezentare grafica a celor stabilite anterior este urmatoarea:

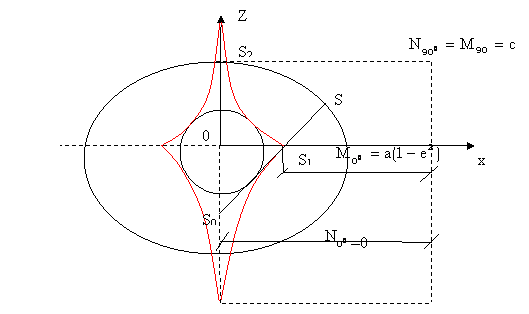
fig. nr. 4

Pentru a reprezenta grafic marimile razelor de curbura ce trec prin punctul S se construieste desfasurata sau evoluta elipsei. Oricare dintre punctele elipsei meridiene au razele de curbura M tangente in interior la evoluta elipsei pe care se determina astfel centrele de curbura. Curba este tangenta in interior la cercul de raza R = a - b. Ecuatia evolutei este urmatoarea:

La elipsele cu turtire mica evoluta este foarte subtire, iar la limita (in cazul cercului) evoluta devine centrul acestuia.

Calculul lungimii arcului de meridian (sm)

Pentru deducerea formulei de calcul a lungimii acestei curbe, alegem pe conturul elipsei meridiane doua puncte infinit apropiate avand aceeasi longitudine, λ, dar cu latitudini diferite: S₁(j l), S₂(j l) unde j > j . Distanta finita dintre acestea o notam cu S_1- In situatia in care, consideram ca punctele sunt infinit apropiate, putem calcula (conform figurii de mai jos) lungimea unui astfel de arc de meridian pornind de la expresia razei de curbura a sectiunii normale principale a elipsei meridiane:

fig. nr. 5

unde s₁-₂ = a(1-e²)

Aceasta este o integrala eliptica de speta I si nu admite solutii imediate, fapt pentru care se va dezvolta in serie expresia din a doua paranteza.

Deoarece |e²sin²j| < 1, seria este convergenta si se calculeaza pana la puterea a opta, pentru a obtine precizia necesara de calcul a lungimii arcului de meridian, tinand cont de formulele puterilor sinusilor, dintre care reamintim:

,

Efectuand calculele, si grupand in mod favorabil, sub forma unor coeficienti, valorile numerice exprimate si in functie de prima excentricitate numerica, notata cu e, obtinem:

In cadrul acestei formule, coeficientii au fost notati cu A', B', C', D' si E' avand expresiile:

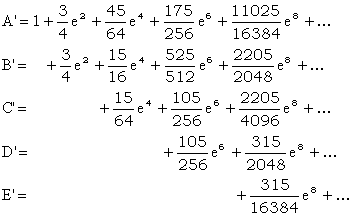
Pentru elipsoidul Krasovski, coeficientii numerici preiau urmatoarele valori:

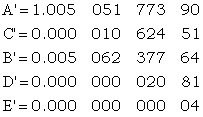
In limita aproximatiilor acceptate, in urma integrarii vom obtine expresia:

In cadrul acestei expresii, se selecteaza coeficientii constanti in functie de latitudine si exprimabili in metri, pentru care se adopta urmatoarele notatii:

pe care ii inlocuim, obtinand forma prescurtata a expresiei de calcul a lungimii finite a arcului de meridian:

Se observa ca, expresia primului termen se masura in radiani si din acest motiv a fost convertita in grade sexagesimale prin intermediul coeficientului ρ◦.

Pentru exemplificarea ordinului de marimi ale acestor constante pentru latitudinea j exprimata in grade sexagesimale in cazul elipsoidului Krasovski vom avea urmatoarele valori medii:

P = 111 134,861 083 803 m

Q =    16 036,480 269 m

R = 16,828 060 67 m

S =    0,021975 m

T =    0,000031 m

Observatii:

1. Lungimea arcului de meridian este functie de parametrii elipsoidului de referinta si de latitudinile j si j ale punctelor ce-l marginesc (situate la capetele arcului de meridian ds_m). Presupunand cunoscute latitudinile precum si lungimea arcului de meridian rezulta o posibilitate de determinare, prin intermediul formulei de mai sus, a parametrilor elipsoidului de referinta (a si e²). Daca dispunem de mai mult de 2 de astfel de masuratori, determinarea parametrilor se poate face in mod riguros, rezolvand sistemul prin metoda celor mai mici patrate, utilizata, cu precadere, in cadrul calculelor de geodezie elipsoidala.

Pentru unele calcule aproximative cu ajutorul relatiilor de mai sus s-au dedus valorile arcelor de meridian astfel:

¾        pentru valori sexagesimale:

¾        pentru valori centesimale:

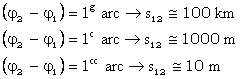
si, in consecinta, pentru 0'',0001 s_1-2 3 mm.

3. In realitate, lungimea arcului de meridian de 1 sexagesimal este in functie de latitudinea j a acestuia, inregistrandu-se o crestere de la ecuator la pol, la fel ca si pentru raza de curbura M a elipsei meridiane:

arc 1 j (Ecuator.) s_1-2 110.576,3 m

arc 1 j (Poli) s_1-2 111.695,8 m

4. Pentru lungimi de arce de meridian < 45 km se utilizeaza o formula de calcul simplificata, in functie de latitudinea medie notata cu j_m j j ) / 2 si diferentei de latitudini Dj j j ambele exprimate in grade sexagesimale.

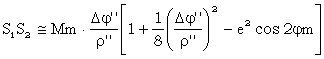
5. Foarte importanta de retinut este formula de calcul a unui element de arc de meridian:

d_sm = Mdj

6. Se observa ca lungimea unui arc de meridian este functie de cele doua latitudini si de parametrii elipsoidului de referinta:

3. Lungimea arcului de paralel s_p. Metoda de determinare a elipsoidului de referinta

Fie doua puncte S₁(j l ) si S₂(j l ) situate pe paralelul de raza r, la distanta finita, notata cu s_p.

fig. nr. 5

In domeniul infinit mic, lungimea arcului de paralel se poate calcula cu relatia: Din cadrul desenului de mai sus se observa ca, din punct de vedere geometric, mai este exprimabil in functie de raza de curbura a sectiunii normale principale a primului vertical. Prin egalarea acestor doua rezultate obtinem:

Deoarece raza cercului de paralel, r este constanta pentru o latitudine data, relatia este integrabila imediat iar lungimea finita a unui arc de paralel are urmatoarea formula:

iar daca pentru elementele constante din formula adoptam notatia putem scrie:

si se observa ca:

iar in cadrul formulei cunoastem:

Observam ca lungimea unui arc de paralel este functie atat de latitudine si longitudini cat si de parametrii elipsoidului de referinta: sp = f(a, e², j l l ), iar .

Formulele de calcul pentru lungimile unui arc de meridian si de paralel ne dau posibilitatea principala de determinare a parametrilor elipsoidului de referinta prin metode geometrice, adica masurand lungimile de arce de meridian si de paralele dintre doua puncte geodezice masurate prin metode astronomo-geodezice, si determinate prin masuratori gravimetrice.

D j l

x h

(j l D

x h

fig. nr. 6

In cadrul figurii de mai sus, cu x h s-au notat valorile acceleratiei gravitationale corespunzatoare celor doua directii normale principale iar cu a, e² s-au notat parametrii elipsoidului de referinta.

4. Elementul liniar al unei curbe( ds) situata pe suprafata elipsoidului de rotatie

I. Presupunem o suprafata oarecare, notata cu S pe care ne alegem un sistem de coordonate curbilinii oarecare pe care, pentru sugestivitate, le notam cu l = const., j = const.

In originea sistemului ducem tangentele la liniile de coordonate curbilinii. Axele x,y dat in origini cu sensul + indreptat spre interiorul suprafetei, perpendiculara pe cele doua axe; alegem axa z a carui directii se suprapune peste normala N la suprafata elipsoidului.

Pentru simplificarea demonstratiei alegem pentru origine coordonatele x₀ = y₀ = z₀ = 0. Prin origine facem sa treaca curba (C) pe care la o distanta infinit mica de origine alegem punctul P. Aceasta se configureaza astfel: elementul liniar ds, in sistemul de coordonate ales, suprafata este definita parametric prin ecuatiile:

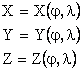
Daca ne propunem sa exprimam elementele de arc ds in raport cu cresterile de coordonate , pentru distante infinit mici, putem aproxima, conform figurii de mai jos:

x

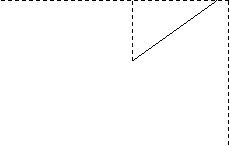
ds dx

dy

fig. nr. 7

y

Pentru acest sistem de coordonate cartezian ortogonal bidimensional, in cazul suprafetelor infinit mici, se poate scrie formula (1) si apoi se particularizeaza pentru un sistem de coordonate tridimensional cu formula (2):

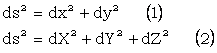
din cadrul careia se exprima derivatele functiilor:

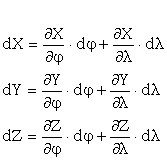
iar reprezinta expresia primei forme patratice fundamentala a lui Gauss in geometria diferentiala in cadrul careia cu E, F, G am notat niste parametri auxiliari ce depind pe de o parte de natura suprafetei, iar pe de alta parte de pozitia punctului pentru care calculam expresiile:

Particularizari:

1. Pentru situatia in care elementul liniar ds merge de-a lungul unui meridian:

Pentru situatia in care elementul liniar ds merge de-a lungul unui paralel:

II. Pe suprafata elipsoidului de referinta, liniile curbilinii sunt paralele cu latitudinea j = const. si meridianele cu longitudinea l = const., ce se intersecteaza, pentru suprafete infinit mici sub unghiuri drepte:

si

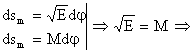
5. Calculul unghiului dintre liniile de coordonate curbilinii (w). Calculul elementului de arie (ds)

I. Pe o suprafata curba oarecare, notata cu S adoptam un sistem de coordonate curbilinii l = const., j = const. Iar la acestea ducem tangentele in origine, notate cu tl respectiv, tj intre care se formeaza unghiul w, in cazul cel mai general diferit de 90⁰. Ne propunem sa calculam unghiul w in functie de parametrii E, F, G. Pentru aceasta definim tangentele tl, tj in functie de cosinusii directori a b g adica cosinusii unghiurilor pe care tangentele il fac cu axele unui sisteme de coordonate ortogonal tridimensional X, Y, Z avand aceeasi origine.

Particularizand pentru planul de proiectie cartografica si pentru suprafete infinit mici, conform figurii, cosinusii directori vor avea urmatoarele expresii:

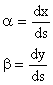
fig. nr. 8

Corespunzator suprafetei S vom avea:

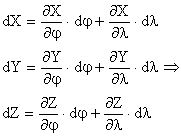
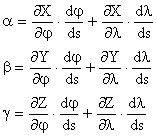
Particularizand pentru tangenta tl a_l b_l d_l

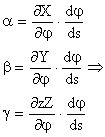
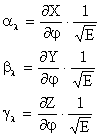
Particularizand pentru tangenta tj a_j b_j d_j

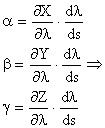
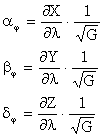
Putem determina si alte formule:

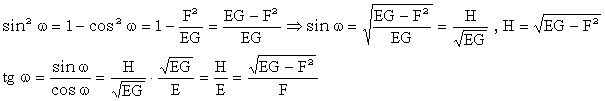
II. Pe suprafata elipsoidului

Pentru calculul elementului de arie:

Pe o suprafata curba oarecare, conform figurii, trebuie calculata aria unui paralelogram: ds = b i

Pentru suprafata elipsoidului

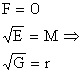
Pentru suprafata unei sfere cu raza R = const.

M = N = R

6. Azimutul geodezic al unei curbe situata pe suprafata elipsoidului de referinta

I. Pentru o suprafata curba oarecare, notata cu S, conform desenului de mai jos, adoptam un sistem de coordonate curbilinii, l = const., j = const. iar la acesta ducem tangentele in origine, notate cu tl a_l b_l d_l) respectiv, tj a_j b_j d_j

fig. nr. 9

Azimutul geodezic, notat cu A, este unghiul masurat, in sens direct sau al acelor de ceasornic, de la tangenta la linia de coordonata l = const. pana la tangenta la curba, notata cu t(a b g) asimilabila, directiei de viza situat de, a lungul acesteia. Pentru obtinerea formulelor de calcul a valorilor functiilor trigonometrice ale azimutului pornim de la relatia stabilita la subiectul anterior:

pe care o particularizam: ,

in cadrul careia deja cunoastem expresiile cosinusilor directori:

Suprafata S este definita de relatiile X = X(j l), Y = Y(j l), Z = Z(j l

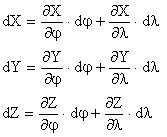
Particularizand pentru tangenta tl a_l b_l d_l

deoarece elementul de arc ds este un element de arc de meridian si in plus cunoastem expresia derivatei

Ne rezulta astfel expresiile particularizate ale cosinusilor directori ai tangentei:

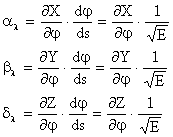
Inlocuind in formula lui cos A, efectuand calculele si grupand favorabil vom obtine:

O alta formula de interes se obtine astfel:

unde cunoastem expresia la patrat a elementului liniar:

si vom obtine:

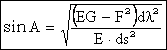
cu ajutorul ultimelor doua rezultate se poate scrie ca:

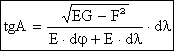
II. Pe suprafata elipsoidului de referinta s-a demonstrat ca:

deoarece, pentru distante infinit mici se considera ca liniile sistemului de coordonate curbiliniu sunt perpendiculare intre ele si in plus:

unde:

fig. nr. 10

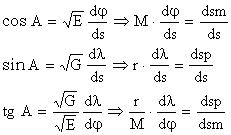
7. Curbura curbelor ce trec printr-un punct situat pe suprafata elipsoidului de referinta

I. Curbura unei sectiuni normale oarecare (curbura unei curbe strambe C)

Presupunem o suprafata curba oarecare F pe care alegem punctul S₁ de coordonate X, Y, Z prin care trec o infinitate de curbe dintre care alegem curba (C) care este o curba stramba necontinuta in nici un plan si cu raza de curbura variabila. Tot aici alegem originea unui sistem de coordonate numit triedru fundamental sau mobil Euler ale carui directii principale sunt:

¾    t ce reprezinta tangenta principala la curba din punctul S₁;

¾    n ce reprezinta normala principala la curba ce este amplasata in planul osculator (planul osculator este planul ce contine doua tangente infinit apropiate);

¾    b reprezinta binormala la curba care este perpendiculara pe planul osculator (bn).

In plus tot prin acest punct trece normala la suprafata F de cosinusi directori N (X', Y', Z'). Ea este unica si este perpendiculara pe planul tangent la suprafata (Nt). Dupa cum stim, planul normal este un plan ce contine normala N la suprafata elipsoidului intr-un punct dat

Triedrul mobil genereaza 3 plane:

¾    planul osculator format de vectorii (n,t);

¾    planul normal format de vectorii (b,n);

¾    planul rectifiant format de vectorii (b,t).

S-a demonstrat faptul ca, printr-o infinitate de curbe putem duce cate o tangenta la fiecare dintre acestea astfel incat, toate tangentele sa fie continute intr-un singur plan, numit planul tangent. In cazul nostru, in planul tangent s-au inclus t, tλ si tφ ultimele doua fiind tangente la liniile de coordonate curbilinii λ = const., respectiv φ = const.

Pe curba stramba, la o distanta infinit mica de originea triedrului, notata cu ds, se alege un punct S₂ (X+dX, y+dY, Z+dZ).

fig. nr. 11

Ne propunem sa determinam expresia de calcul a curburii pe care o notam cu 1/r a acestei curbe strambe a carei raza de curbura variabila o notam cu r. Pentru aceasta exprimam cosinusul unghiului dintre vectorii n si t:

Cosinusi directori ai acestor directii admit derivate partiale pana la ordinul doi inclusiv, cunoscute sub denumirea de formulele lui Frênet pe care le vom prelua in continuare

a. (ordinul I) care definesc cosinusi directori ai tangentei t la curba;

b. (ordinul I) care definesc cosinusii directori ai normalei n la curba.

Pentru calculul curburii diferentiem total relatia de mai sus pe care o putem scrie generic ca fiind:

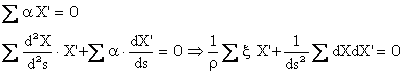
in cadrul careia relatia anterioara exprima unghiul ψ dintre normala t in punctul S₁ si normala principala la curba n in cazul unei suprafete oarecare.

in cadrul careia se cunosc expresiile:

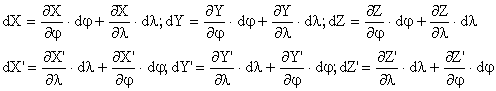
precum si

Efectuand calculele si grupand favorabil termenii ce contin derivatele partiale in cazul sumei ådXdX' vom obtine expresia:

expresie ce reprezinta cea de-a doua forma patratica fundamentala a lui Gauss in geometria diferentiala, iar coeficientii sunt niste parametrii ce depind, pe de-o parte de natura suprafetei iar pe de alta parte de pozitia punctului S

Intre coeficientii celor doua forme patratice fundamentale exista relatii de interdeterminare numite relatii Gauss-Codazzi

Aceste doua forme fundamentale definesc in mod complet, din punct de vedere matematic, suprafata S.

II.     In cazul elipsoidului de referinta

Deoarece liniile de coordonate curbilinii sunt ortogonale avem:

In continuare ne propunem sa determinam formulele de calcul pentru coeficientii D'', D.

Pornind de la ecuatiile parametrice ale elipsoidului de rotatie:

in cadrul carora:

fig. nr. 12

Cosinusii directori ai coordonatelor X', Y', Z' se calculeaza prin proiectarea versorului de normala n si lungimea egala cu unitatea pe cele trei axe de coordonate ale sistemului X, Y, Z.

Conform desenului de mai jos, putem scrie ca:

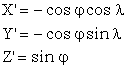
iar derivatele partiale ale functiilor in raport cu longitudinea sunt:

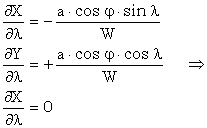
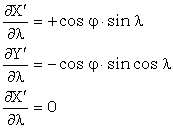
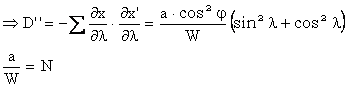
In cazul elipsoidului de referinta, fara demonstratie, rezulta ca: astfel incat, expresiile parametrilor celei de-a doua forma patratica fundamentala vor fi:

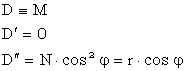
Cu ajutorul relatiei curburii unei curbe strambe am stabilit modul de calcul a curburii oricarei curbe strambe situata pe suprafata oarecare F.

In cazul elipsoidului de referinta ne-am propus sa calculam, de fapt, curbura unei sectiuni normale.

In acest caz particular normala principala la curba n se identifica cu normala N la suprafata elipsoidului (n º N) situatie in care, unghiul y = 0⁰ si cosj

Daca notam raza de curbura a sectiunii normale cu R_n, curbura sectiunii normale va fi:

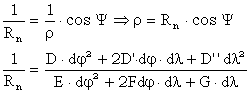
Relatia se numeste formula lui Meusnier.

O alta curbura de interes este curbura unei sectiuni geodezice ce semnifica totodata tangenta la curba, avand notatia in cadrul careia R_g reprezinta raza curburii geodezice.

Am stabilit ca r este, in cazul general, raza de curbura a unei curbe strambe oarecare pe care am particularizat-o pentru elipsoid. Ea reprezinta insa o curba provenita dintr-o sectiune inclinata oarecare care, conform teoremei lui Meusnier are aceeasi tangenta la suprafata elipsoidului in punctul dat cu sectiunea normala principala a primului vertical de raza de curbura N.

Prin similitudine, in formula putem considera ca unghiul dintre cele doua sectiuni este chiar latitudinea j a punctului dat.

8 Expresia razei de curbura a unei sectiuni normale in functie de azimutul geodezic.

Raza de curbura a unei sectiuni normale se noteaza cu R_n iar daca o exprimam in functie de azimutul geodezic, se noteaza cu R_A. Curbura acestora are expresia cunoscuta:

si mai s-au stabilit, in cazul elipsoidului de rotatie, relatiile de compatibilitate Gauss - Codazzi intre parametrii celor doua forme patratice fundamentale:

astfel incat putem scrie:

in cadrul careia numitorul reprezinta expresia elementului liniar la patrat (ds²)

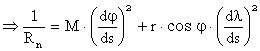unde ds_m reprezinta un element de arc de meridian: ds_m = M dφ iar ds_p reprezinta un element de arc de paralel: ds_p = r dλ, astfel incat obtinem :

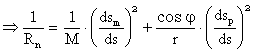fig. nr. 13

Tinand cont si de alte expresii cunoscute:

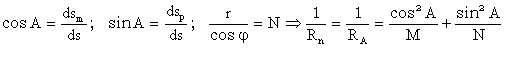
Aceasta se numeste formula lui Euler ce reprezinta valoarea curburii unei sectiuni normale exprimata in functie de azimutul geodezic.

Pozitiile sectiunilor normale principale care trec printr-un punct P de pe suprafata elipsoidului se pot deduce din relatia de mai sus prin utilizarea conditiilor de minim si de maxim:

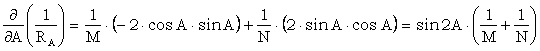
Cu aceasta relatie determinam valorile minime si maxime ale azimutului geodezic si ale razelor de curbura ale sectiunilor normale principale. Astfel:

¾    pentru A = 0^o avem sectiunea de raza minima, M, a elipsei meridiene;

¾    pentru A = 90^o avem sectiunea de raza maxima, N, a primului vertical.

Se constata ca:

9. Raza medie de curbura, R_m sau raza sferei medii Gauss

Dupa cum se stie, expresia curburii unei sectiuni normale exprimata in functie de azimutul geodezic este:

In cadrul acestui subiect ne propunem sa urmarim modul de deducere a unei formule de calcul pentru valoarea unei raze medii de curbura, notata cu R_m, a tuturor sectiunilor normale ce trec prin punctul P, de latitudine φ, situat pe suprafata elipsoidului de rotatie, determinata de matematicianul F. K. Gauss. Dupa cum stim, aceasta poate fi minima, pentru sectiunea normala principala a elipsei meridiene, M, sau maxima, pentru sectiunea normala principala a primului vertical, N. Aceasta raza este utila pentru simplificarea calculelor geodezice si cartografice dar se utilizeaza la nivel teritorial limitat, niciodata insa pentru intreaga suprafata terestra.

Daca privim spre punctul P, de-a lungul normalei lui la suprafata elipsoidului de rotatie vom observa ca prin el trec, pe langa cele doua sectiuni normale principale a caror imagine este de drepte perpendiculare, o infinitate de curbe ce reprezinta sectiuni normale diferite intre ele prin curbura, functie de valoarea azimutului geodezic, A, conform figurii de mai jos:

fig. nr. 14

Particularizand formula lui Euler pentru raza unei sectiuni normale exprimata in functie de azimutul geodezic, vom obtine:

Pornind de la aceasta relatie putem defini raza medie Gauss ca fiind:

sau, mai convenabil pentru calcule:

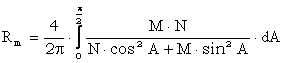, relatie care se imparte, fortat, atat la numarator cat si la numitor cu la N cos²A:

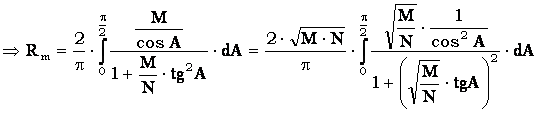
Pentru obtinerea ultimei expresii s-a scos de asemenea fortat, din integrala constanta . Daca adoptam urmatoarea notatie:

unde, pentru

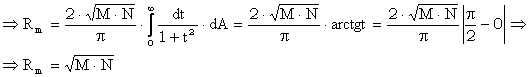
Aceasta reprezinta expresia de calcul a razei medii de curbura Gauss atunci cand numarul sectiunilor normale tinde catre infinit. Din studiul formulei se observa ca aceasta depinde de razele de curbura ale sectiunilor normale principale conjugate (minima a sectiunii meridiene, notata cu M) si maxima (a sectiunii primului vertical, notata cu N).

Expresiile razelor de curbura se cunosc si prin intermediul lor ne propunem sa obtinem si alta formula de calcul pentru raza medie Gauss:

Utilizand aceste relatii rezulta ca:

Aceasta ultima relatie poate fi utilizata pentru studiul valorilor minime si maxime ale razei medii, in functie de latitudinea punctului P:

Astfel, la ecuator, pentru

iar la pol, pentru

In plus fata de formula de calcul a razei medii, in geodezia elipsoidala se mai utilizeaza formula de calcul a curburii totala, notata K: si curbura medie, notata cu H: ce depind, de asemenea de latitudinea φ a punctului P si care se preiau fara demonstratie.

10. Sectiunea normala directa si sectiunea normala inversa. Pozitia lor reciproca

Fie punctele S₁ (φ₁, λ₁) si S₂ (φ₂, λ₂) cu situate pe suprafata elipsoidului de rotatie, proiectate pe axa polilor in punctele prin intermediul normalelor N₁, si N₂ conform figurii nr. 15:

figura nr. 15

Consideram punctele S₁ si S₂ ca apartinand unei retele geodezice si care au fost stationate in vederea efectuarii de observatii azimutale reciproce. Planele formate de normalelor N₁ si N₂ si punctele S₁ si S₂ vor reprezenta planul vizelor si vor intersecta suprafata elipsoidului dupa doua curbe, notate cu a si b ce se numesc sectiuni normale principale reciproce. Astfel planul ce contine normala N₁ si punctul S₂ va intersecta suprafata dupa curba a ce se numeste sectiunea normala directa a punctului S₁ in raport cu punctul S₂ iar planul ce contine normala N₂ si punctul S₁ va intersecta suprafata dupa curba b ce se numeste sectiunea normala directa a punctului S₂ in raport cu punctul S₁.In continuare ne propunem sa demonstram atat raportul valori dintre doua segmente () si sa stabilim formula de calcul a segmentului ce ne vor folosi in cadrul unor rezolvari ulterioare.

Din studiul figurii se observa ca:

Datorita valorii mici se aproximeaza: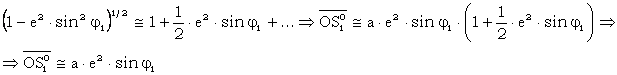

In mod analog rezulta ca:

In continuare:

Deoarece cele doua puncte sunt foarte apropiate, se aproximeaza:

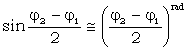
si se noteaza

Observatii:

1. In cazul in care cele doua puncte se afla pe acelasi meridian (λ₁ = λ₂) sau pe acelasi paralel (φ₁ = φ₂) cele doua sectiuni reciproce coincid.

Referitor la notiunile de sectiuni normale se constata ca acestea reprezinta niste curbe rezultate din intersectia planului normal (planul de viza) format de normala punctului stationat (care dupa calarea aparatului o consideram suprapusa peste axa principala VV a acestuia) si punctul vizat, notat cu a si invers.

In consecinta se poate spune ca, observatiile de directii azimutale efectuate intr-un triunghi geodezic S₁ S₂ S₃ vor avea drept corespondente la transpunerea lor pe suprafata elipsoidului 6 curbe (3 sectiuni directe si 3 sectiuni inverse) care nu vor realiza o figura geometrica continua si inchisa, conform figurii nr. 16 De aici rezulta necesitatea prelucrarii prealabile a observatiilor inainte de a fi efectuate calculele. Prin aceste prelucrari se trece de la dualitatea sectiunilor directa si inversa dintre doua puncte la o linie imaginara (curba) numita linie geodezica.

fig. nr. 16

11. Linia geodezica: definitie, ecuatia in termeni finiti pentru linia geodezica a lui Clairaut

Linia geodezica este o curba pe o suprafata astfel construita incat, in toate punctele sale, planul osculator, format din vectorii n si t sa contina normala N la suprafata elipsoidului deci n N. In consecinta, in oricare din punctele sale, curbura geodezica va fi nula deoarece unghiul dintre cele doua normale este si el nul:

Pe suprafata elipsoidului numai meridianele si cercul ecuatorial sunt linii geodezice iar pe suprafata sferei toate cercurile mari, deoarece in planul lor este continuta normala N (si deci paralelele nu sunt linii geodezice).

Trecerea de la sectiunile normale la linia geodezica se face prin aplicarea unor corectii.

fig. nr. 17

Pentru figura nr. 17 ce reprezinta sectiunile si linia geodezica a celor doua puncte geodezice stationate, ecartul dintre sectiuni, notat cu q precum si marimile unghiulare Δ si Δ/3 se dau formulele de calcul:

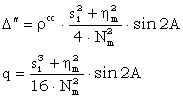
Pentru distante geodezice mici adica km

Dupa cum stim expresia curburii unei curbe oarecare este: iar pe suprafata elipsoidului de referinta Ψ = 0 deci cos Ψ = 0 situatie in care valoarea curburii va fi minima, tinzand catre o linie dreapta.

La limita, in domeniul infinit mic, elementul de linie geodezica este continut in planul tangent fapt pentru care, linia geodezica mai este definita ca: cel mai scurt drum dintre doua puncte pe o suprafata.

Fie punctele S₁ si S¢ situate pe acelasi cerc de paralel. Tangentele duse in aceste puncte la planele lor meridiane se vor intersecta pe prelungirea axei polilor in punctul T formand intre ele unghiul dA ce se mai numeste si unghi de convergenta meridiana.

Presupunem ca S₁ este punctul de statie, iar punctul S₂ este punctul vizat. Directia de la S₁la S₂ este linia geodezica si dupa cum stim, in domeniul infinit mic, la limita, segmentul de linie geodezica S₁S₂ tinde sa vina in planul tangent.

Di studiul figurii nr. 2.pentru triunghiul TO₁S, dar in acelasi timp putem exprima segmentul S₁S₁ = rd, dar conform figurii mai este egal cu .

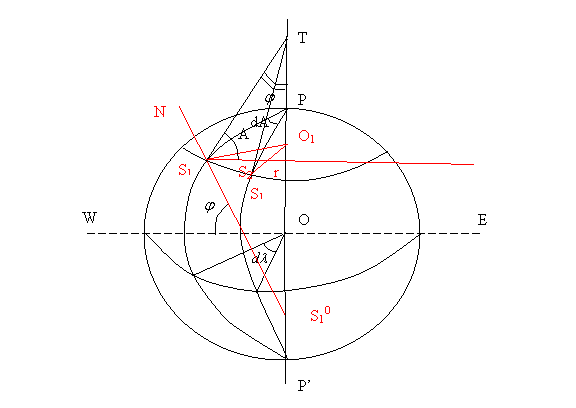
figura nr. 18.a

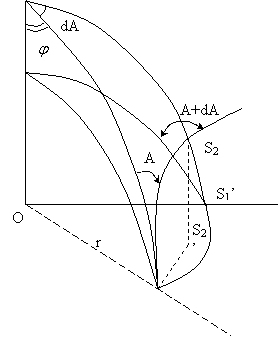
figura nr. 18.b

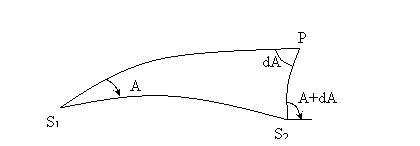
figura nr. 218.c

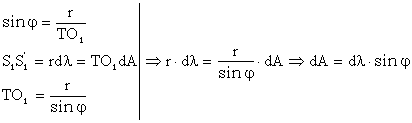
Aceasta se numeste formula lui Clairaut pentru calculul convergentei meridianelor.

In continuare, consideram cunoscute urmatoarele formule:

; r = x

dr = -M , M=

=

Integram aceasta relatie si obtinem:

Aceasta se numeste ecuatia in temeni finiti a lui Clairaut pentru linia geodezica

1 Ecuatiile parametrice ale liniei geodezice (ecuatiile PUISEAUX-WEINGARTEN-GAUSS)

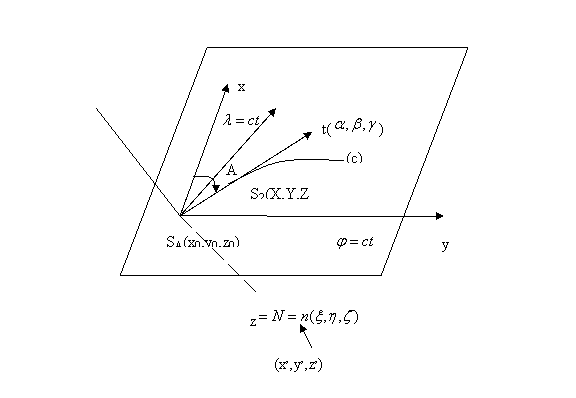
fig. nr. 19

Fie punctele S₁ (X₀, Y₀, Z₀) si S₂ (X, Y, Z) situate pe curba (c) pe o suprafata curba F la o distanta infinit mica. Curba o identificam cu linia geodezica. Suprafata noastra F este definita implicit de relatia F(X, Y, Z) = 0, iar linia geodezica este definita de ecuatiile parametrice: X = X(s), Y = Y(s), Z = Z(s), deoarece prin deplasarea pe curba punctul s isi schimba parametrii in functie de lungimea, s, a liniei geodezice.

Functiei F i se aplica o dezvoltare in serie McLaurin:

f(x) = f(0) + x() + x²()+ x³ (

X = X(s) = X₀ + s + + +

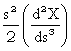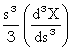Y = Y(s) = Y₀ + s + + +

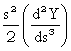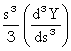Z = Z(s) = Z₀ + s + + +

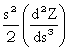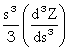Vom determina ecuatiile parametrice ale liniei geodezice punand niste conditii suplimentare adica presupunand ca s60Km este o distanta geodezica mica si ca X₀ = Y₀ = Z₀ = 0. Apelam la formulele lui Frnet de ordinul I, II, III:

unde dupa cum stim reprezinta curbura liniei geodezice a carei expresie, in functie de azimut, o cunoastem iar ρ reprezinta raza de curbura a curbei cu expresia: unde este egal cu unghiul dintre doua tangente infinit apropiate.

reprezinta torsiunea curbei si poate fi exprimata:sinA cosA

iar raza de torsiune a curbei este: unde ^, este egal cu unghiul dintre 2 plane osulatoare infinit apropiate.

Tinand cont de faptul ca t este perpendicular pe Z si ca in apropierea originii, intre tangenta t si axa oX se formeaza azimutul geodezic A, se calculeaza expresiile derivatelor de ordinul I, II, III si in apropierea originii sistemului:

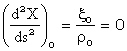
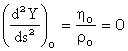
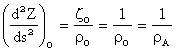
Curbura liniei geodezice functie de azimut este:

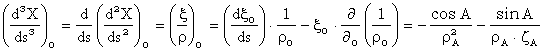
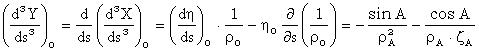
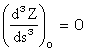
Cunoscand ca:

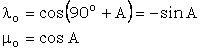
O acceptam ca fiind nula deoarece in cazul elipsoidului coordonata Z reprezinta practic altitudinea punctelor, iar in geodezie aceasta se determina, separat fata de planimetrie, numai prin nivelment trigonometric geodezic metoda care nu se poate aplica cu precizie la distante mai mari de 6 Km. In continuare, aceste expresii se prelucreaza tinand cont de:

, astfel incat se obtin:

X = s cosA +

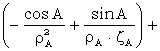
Y = s sinA+

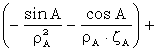
Z=+

De unde:

X = s cosA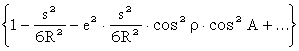

Y = s sinA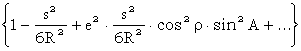

Z =

Acestea se numesc ecuatiile parametrice ale liniei geodezice sau ecuatiile PUISEAUX-WEINGARTEN-GAUSS.

Consecinte:

In geodezie nu se lucreaza intr-un sistem tridimensional X, Z, Z, uniform ci se rezolva separat problema planimetrica (X, Y) fata de cea altimetrica prin utilizare de tehnologii de lucru complet diferite. Planimetria se rezolva prin triangulatie, trilateratie, poligonatie pentru s60Km. Altimetria se rezolva prin nivelment trigonometric geodezic cu rezultate bune pentru s pana in 1 sau 2 Km.

In functie de lungimile s ale liniei geodezice influenta termenilor din paranteza este diferentiata astfel pentru lungimea liniei geodezice s6km consideram ca lucram in domeniul planimetric, termenii din paranteza au valori neglijabile. Cand avem al doilea termen incepe sa aiba semnificatie matematica si consideram ca lucram in domeniul sferic local, adica suprafata elipsoidului de referinta se poate inlocui cu suprafata sferei de raza medie Gauss. Cand s60 km consideram ca lucram in domeniul elipsoidic situatie in care se observa influenta tuturor termenilor din parantezele de mai jos.

X = s cosA{ 1-

Y = s sinA{ 1-

Pentru domeniul geodezic cand s < 60 km = distante mici, cand = distante geodezice medii iar cand distante geodezice mari.