| CATEGORII DOCUMENTE |
| Demografie | Ecologie mediu | Geologie | Hidrologie | Meteorologie |
SUPRAFETE DE REFERINTA. SISTEME DE COORDONATE
1. Suprafete de referinta
Masuratorile geodezice se realizeaza pe suprafata fizica a Pamantului care este o suprafata complexa si deloc neteda. Pentru obtinerea unor coordonate unitare ale punctelor retelei geodezice de sprijin, aceste masuratori trebuie referite la o suprafata unica, care, pe de-o parte, sa aproximeze (prin uniformizare) cat mai bine suprafata terestra si careia, pe de alta parte, sa i se cunoasca dimensiunile. In urma unor cercetari aprofundate s-a stabilit initial ca aceasta ar fi suprafata unui sferoid de rotatie. Ulterior s-a convenit ca, suprafata, avand ca imagine fizica, intr-o aproximare destul buna, suprafata medie si linistita a marilor si oceanelor (adica atunci cand aceasta se afla in echilibru) prelungita pe sub continente, satisface aceste cerinte. Aceasta este o suprafata de nivel inchisa, fara nici o muchie dar ondulata. Corpul geometric foarte complicat format de o astfel de suprafata se numeste geoid.
Suprafata geoidului terestru este determinabila prin masuratori locale de astronomie geodezica, geodezie fizica (gravimetrie) si topografie (nivelment de stat de ordin superior) dar nu este determinabila din punct de vedere matematic, motiv pentru care este utilizata numai ca suprafata de referinta altimetrica.
Corpul care aproximeaza cel mai bine geoidul si in acelasi timp se supune unor legi matematice cunoscute este elipsoidul de rotatie cu turtire mica la poli ce se mai numeste si elipsoid terestru de rotatie. Aceasta notiune a fost introdusa in anul 1600 de catre fizicianul englez Isaac Newton sub denumirea de elipsoid de revolutie terestru.
a. elipsoidul
Elipsoidul de rotatie este un corp matematic generat prin rotirea unei elipse in jurul axei sale mici ce se suprapune peste axa polilor geografici. In cadrul figurii 1.1 este prezentata o sectiune meridiana a elipsoidului iar din studiul acesteia se observa urmatoarele:
¾ perpendicular
pe axa polilor geografici, notata cu PNPS, impartind-o in
doua segmente egale ca lungime: ![]() (ce se numesc semiaxele mici ale elipsoidului)
se afla directia cardinala WE cuprinsa in planul ecuatorial elipsoidal care, la
randul ei este impartita in doua segmente egale ca lungime:
(ce se numesc semiaxele mici ale elipsoidului)
se afla directia cardinala WE cuprinsa in planul ecuatorial elipsoidal care, la
randul ei este impartita in doua segmente egale ca lungime: ![]() (ce se numesc semiaxele mari ale
elipsoidului);
(ce se numesc semiaxele mari ale
elipsoidului);
¾ aceste doua directii se intersecteaza in punctul O ce reprezinta centrul matematic al elipsoidului.
Semiaxa mare, notata cu a si semiaxa mica, notata cu b reprezinta parametri elipsoidali. Descrierea completa a unui elipsoid de rotatie se poate face, prin intermediul a doi parametrii, dintre care, in mod obligatoriu, unul trebuie sa fie liniar. Acesti parametri se numesc parametrii principali.
De regula sunt utilizate semiaxa mare notata cu a, cunoscuta si sub denumirea de raza ecuatoriala si turtirea geometrica, notata cu α pentru care, in literatura de specialitate se mai intalneste notatia f:
![]()
![]()
Dupa cum se observa, turtirea elipsoidului terestru are o valoare destul de mica.
figura nr. 1.1
Parametrii secundari ai elipsoidului de referinta sunt:
![]() reprezinta semiaxa mica sau raza
polara; (2)
reprezinta semiaxa mica sau raza
polara; (2)
![]() ce se numeste prima excentricitate numerica; (3)
ce se numeste prima excentricitate numerica; (3)
![]() ce se numeste a doua excentricitate
numerica; (4)
ce se numeste a doua excentricitate
numerica; (4)
4. ![]() ce se numeste excentricitatea lineara; (5)
ce se numeste excentricitatea lineara; (5)
5. ![]() ce se numeste raza de curbura polara. (6)
ce se numeste raza de curbura polara. (6)
Intre parametrii principali si secundari ai elipsoidului de referinta se pot stabili, prin calcule simple, diverse relatii matematice. Astfel, din prelucrarea relatiei (1) rezulta:
![]()
![]() (7)
(7)
![]() (8)
(8)
Din prelucrarea relatiei (2) rezulta:
![]() (9)
(9)
![]() (10)
(10)
Aceasta aproximatie se numeste aproximatie de ordinul I si este permisa, tinandu-se cont de valoarea mica a turtirii.
![]() (11)
(11)
Din prelucrarea relatiei (3) rezulta:
![]()
![]() (12)
(12)
Prin egalarea relatiilor (10 ) si (11) rezulta:
![]()
![]() (13)
(13)
In mod analog, se obtin relatiile:
![]()
Din punct de vedere practic insa, se lucreaza cu elipsoidul de referinta care este determinat din punct de vedere a marimii parametrilor si definit ca fiind acel elipsoid utilizat, la un moment dat, de catre un stat sau un grup de state pentru rezolvarea problemelor geodezice, in speta pentru intocmirea hartilor topografice de baza.
De-a lungul timpului, functie de stadiul dezvoltarii stiintelor masuratorilor terestre (in ceea ce priveste posibilitatile de determinare a coordonatelor punctelor geodezice) sau a dezvoltarii tehnologice au existat mai multe metode de determinare a parametrilor elipsoidului de referinta:
¾ metode geometrice: bazate pe masuratori de distante efectuate in cadrul unor lanturi de triangulatie (statale sau internationale) dispuse de-a lungul meridianelor si paralelelor.
¾ metode fizice ce se bazeaza pe masuratori gravimetrice;
¾ metode satelitare.
b. sfera
Spre deosebire de elipsoid, sfera este un corp de rotatie mai abordabil din punct de vedere matematic deoarece are raza constanta. Sfera este corpul matematic de rotatie generat prin rotirea unui cerc de raza medie in jurul diametrului sau ce se suprapune a fi suprapus peste axa polilor geografici PNPS, si trece prin centrul de masa al Pamantului. In cadrul sferei de rotatie se neglijeaza turtirea la poli deoarece, cu precadere, aceasta suprafata se utilizeaza in cartografie in cazul reprezentarilor la scari medii si mici (pentru intocmirea hartilor geografice). Aceasta suprafata matematica de referinta se adopta si in geodezie in doua situatii:
¾ atunci cand utilizarea sferei nu influenteaza precizia de determinare a elementelor necesare;
¾ atunci cand calculele geodezice ar fi extrem de laborioase utilizand ca suprafata de referinta matematica elipsoidul.
In acest caz trebuie calculata valoarea unei raze media sferei si functie de scara, tematica, scopul pentru care se intocmeste harta, etc. exista mai multe posibilitati de calcul a acesteia:
ca medie aritmetica:
Rm
= ![]() (15)
(15)
ca medie ponderata:
![]() (16)
(16)
in cazul proiectiilor echivalente se pune conditia ca ariile de pe suprafata terestra sa se reprezinte nedeformate din punct de vedere valoric in planul de proiectia cartografica si pentru aceasta se pune conditia de echivalenta intre suprafata elipsoidului si cea a sferei astfel incat, formula de calcul a razei medii este urmatoarea:
Rm = a( 1- ![]() e2) (17)
e2) (17)
In geodezie insa, in situatiile mai sus amintite, se obisnuieste sa se calculeze raza medie cu urmatoarea formula:
Rm = ![]() =
= ![]() (18)
(18)
determinata de catre matematicianul Karl Frederik Gauss in cadrul careia notatiile au urmatoarea semnificatie:
¾ M reprezinta raza de curbura a sectiunii normale principale meridiane;
¾ N reprezinta raza de curbura a sectiunii normale principale a primului vertical;
¾ c reprezinta raza de curbura polara;
¾ V
reprezinta o notatie auxiliara: ![]()
Prin intermediul
acestei formule valoarea razei medii este calculabila in functie de latitudinea
geografico - geodezica, notata cu![]() , care poate
fi cea corespunzatoare centrului teritoriului de reprezentat, centrului de
greutate al unui triunghi geodezic sau mijlocului unei directii de azimut
oarecare. Din acest considerent, o astfel de sfera de raza medie nu
poate inlocui in totalitate suprafata elipsoidului de referinta ci numai
portiunea din suprafata acestuia situata la latitudinea pentru care s-a
calculat.
, care poate
fi cea corespunzatoare centrului teritoriului de reprezentat, centrului de
greutate al unui triunghi geodezic sau mijlocului unei directii de azimut
oarecare. Din acest considerent, o astfel de sfera de raza medie nu
poate inlocui in totalitate suprafata elipsoidului de referinta ci numai
portiunea din suprafata acestuia situata la latitudinea pentru care s-a
calculat.
2. Sisteme de coordonate
In cadrul geodeziei exista mai multe criterii de clasificare a sistemelor de coordonate dintre care, se pot enumera urmatoarele:
in functie de pozitia originii sistemului de coordonate:
¾ sistem de coordonate geocentric cu originea in centrul matematic al corpului de rotatie;
¾ sistem de coordonate cvasigeocentric cu originea in centrul de masa al Pamantului;
¾ topocentric, cu originea in punctul de statie.
dupa forma:
¾ sisteme de coordonate carteziene;
¾ sisteme de coordonate elipsoidale;
¾ sisteme de coordonate naturale, in cadrul carora se inscriu: sistemele de coordonate geografico - geodezice, sistemele de coordonate astronomice si sistemele de coordonate astronomo - geodezice.
daca ne referim la pozitia unui corp in miscare, de exemplu cea a unui satelit artificial putem avea:
¾ sistem de coordonate satelitcentric;
¾ sistem de coordonate geocentric sideral;
¾ sistem de coordonate orbital.
Dintre acestea vor fi prezentate cele mai utilizate atat in domeniul geodeziei cat si al cartografiei matematice.
A. Sisteme de coordonate ale elipsoidului
a. Sistemul de coordonate tridimensionale carteziene (X, Y, Z)
Este un sistem de coordonate ortogonale, tridimensional, unitar, atat din punct de vedere al unitatii de masura (metrica), cat si din punct de vedere al suprafetei de referinta unica, pentru cele trei coordonate. Din punct de vedere al originii sistemul de coordonate este geocentric.
Axa Z se suprapune peste axa polilor cu sensul pozitiv spre polul Nord, fiind perpendiculara pe planul ecuatorial in centrul matematic al elipsoidului. Axele X si Y sunt continute in planul ecuatorial, perpendiculare una pe cealalta, axa X reprezentand intersectia dintre planul ecuatorial si planul meridianului Greenwich (meridianul origine pentru masurarea longitudinilor) cu sensul pozitiv indreptat spre acesta iar axa Y avand sensul pozitiv spre directia cardinala Est, conform figurii nr. 1.2.
In cadrul acestui sistem, valoarea coordonatelor unui punct de pe suprafata elipsoidului, de exemplu ale punctului S (XS, YS, ZS) se determina prin proiectarea acestuia pe cele trei axe de coordonate carteziene. Pentru determinarea coordonatei ZS se proiecteaza punctul pe axa Z printr-o linie paralela cu planul ecuatorial sau continuta in planul cercului de paralel corespunzator. Pentru determinarea coordonatelor plane XS si YS se proiecteaza, intr-o prima etapa punctul in S' continut in planul ecuatorial. Prin acesta se duc apoi paralele la axele de coordonate. In final, coordonatele vor fi valoric egale cu lungimile segmentelor rezultate:

figura nr. 1.2
Acest sistem de coordonate este utilizat in geodezia tridimensionala (geodezia geometrica spatiala) care reprezinta o ramura relativ recent constituita a geodeziei si care are ca principal scop definirea, intr-un sistem unitar in spatiul tridimensional, a coordonatelor punctelor retelelor geodezice de sprijin.
b. Sistemul de coordonate geografico - geodezice (φ, λ, ΗE)
Latitudinea si longitudinea geografico-geodezice sunt
coordonate unghiulare si se masoara in grade sexagesimale. Latitudinea ![]() a unui punct S situat pe suprafata fizica este
unghiul pe care il face normala N la suprafata elipsoidului in punctul
corespunzator punctului nostru S cu planul ecuatorial. Normala este
perpendiculara pe tangenta dusa la suprafata elipsoidului in punctul respectiv.
Toate punctele avand aceasi latitudine se situeaza pe un cerc de paralel de
raza constanta cu atat mai mica cu cat ne apropiem de poli. Cercul de paralel
de raza maxima este cercul ecuatorial cu latitudinea de O0.
Latitudinile pot fi nordice si sudice, preluand valori intre 00 si
900
a unui punct S situat pe suprafata fizica este
unghiul pe care il face normala N la suprafata elipsoidului in punctul
corespunzator punctului nostru S cu planul ecuatorial. Normala este
perpendiculara pe tangenta dusa la suprafata elipsoidului in punctul respectiv.
Toate punctele avand aceasi latitudine se situeaza pe un cerc de paralel de
raza constanta cu atat mai mica cu cat ne apropiem de poli. Cercul de paralel
de raza maxima este cercul ecuatorial cu latitudinea de O0.
Latitudinile pot fi nordice si sudice, preluand valori intre 00 si
900
Longitudinea este unghiul diedru format de planul meridianului Greenwich cu planul meridianului locului ce trece prin punctul respectiv. Totalitatea punctelor cu aceeasi longitudine definesc un meridian ce reprezinta un arc cu raza de curba variabila in functie de valoarea latitudinii. Longitudinile pot fi estice (pozitive) sau vestice (negative) conform cu pozitia meridianului locului fata de meridianul origine Greenwich si preiau valori intre 00 si 1800.
figura nr.1.3
Altitudinea sau cota elipsoidala HE are doua componente: altitudinea ortometrica, notata cu HORT, ce reprezinta inaltimea punctului masurata prin nivelment fata de suprafata geoidului si ondulatia geoidului, notata cu N, care este diferenta dintre suprafata geoidului si cea a elipsoidului.
HE = HORT + N
Normala N la suprafata elipsoidului proiecteaza punctul respectiv pe axa polilor, in general altundeva decat in centrul de masa al elipsoidului. Ea ajunge in centrul de masa atunci cand se suprapune peste axa polilor sau este continuta in planul ecuatorial.
figura nr.1.4
Intre coordonatele acestor doua sisteme elipsoidale exista urmatoarele relatii ce vor fi deduse ulterior, in cadrul prezentului curs.

c. Sistemul de coordonate geografice (φ, λ)
Se aseamana cu cel anterior dar are ca suprafata matematica de referinta sfera. Este utilizat pentru realizarea hartilor in general in domeniul geografiei dar si in domeniul stiintelor masuratorilor terestre, in doua situatii:
¾ atunci cand calculele geodezice sau cartografice sunt prea dificile utilizand elipsoidul;
¾ atunci cand precizia de determinare a unor valori nu este afectata de utilizarea sferei.
Latitudinea este unghiul format de verticala locului, numita si normala la suprafata geoidului, in acel punct cu planul ecuatorial sferic, iar verticala locului trece intotdeauna prin centrul sferei. Longitudinea se defineste la fel ca si in cazul sistemului de coordonate geografico - geodezice, anterior prezentat.
figura nr.1.5
c. Sistemul de coordonate geocentrice sferice (φ', λa, R)
In cazul in care utilizam observatiile efectuate de catre satelitii artificiali in diferite probleme de astronomie, geodezie, gravimetrie sau in telecomunicatii, meteorologie, navigatie, etc. este necesar sa cunoastem atat pozitia statiilor de observare cat si cea a satelitului. Acestea pot fi definite in mai multe sisteme de coordonate, unul din ele fiind sistemul geocentric sferic.
figura nr. 1.6
In cadrul figurii, R reprezinta raza vectoare adica distanta de la centrul de masa al Pamantului la satelit, φ' este latitudinea geocentrica, λa este longitudinea astronomica. Initial se determina coordonatele astronomice, φa, λa iar apoi latitudinea geocentrica se determina cu urmatoarele formule:
![]()
in cadrul carora S si C sunt marimi ce se datoreaza fenomenului de paralaxa calculabile in functie de φa. Legatura dintre aceste coordonate sferice si coordonatele geocentrice tridimensionale elipsoidale este data de urmatorul grup de formule:
X = Rcos![]() cos
cos![]() = (N+H)cos
= (N+H)cos![]() cos
cos![]()
Y = Rcos![]() sin
sin![]() = (N+H)cos
= (N+H)cos![]() sin
sin![]()
Z = Rsin![]() = (N(1-e2)+H)sin
= (N(1-e2)+H)sin![]()
in cadrul carora N este raza de curbura a sectiunii normale principale a primului vertical.
Daca, in schimb, se cunosc coordonatele carteziene tridimensionale ale statiei, notate tot cu X, Y, Z, se pot determina coordonatele geografico - geodezice ale acesteia cu urmatorul grup de formule:

Un punct situat pe suprafata fizica a Pamantului este in permanenta supus la actiunile unor forte: forta de atractie terestra sau a altor corpuri ceresti precum si forta centrifuga, datorata rotatiei Pamantului in jurul axei sale. Forta rezultanta se numeste gravitate sau greutate, directia sa suprapunandu-se directiei firului cu plumb, cunoscuta sub numele de verticala locului, V. Aceasta este perpendiculara pe planul tangent in proiectia punctului la suprafata de nivel. Dupa calarea perfecta a instrumentului de lucru ea coincide cu axa principala a acestuia, notata cu VV.
Aceasta prima directie fundamentala din natura, la care se refera masuratorile geodezice, trebuie luata in considerare la adoptarea si utilizarea diferitelor sisteme de referinta. Asa dupa cum s-a vazul, in cadrul sistemului de coordonate geografico-geodezice (φ, λ, HE) altitudinea elipsoidala, notata cu HE are doua componente:
HE = H + N
H este altitudinea unui punct P de pe suprafata terestra, determinata prin masuratori de nivelment, fata de o suprafata de referinta materiala (geoidul);
N este ondulatia geoidului, ce se determina prin calcul fata de o suprafata de referinta imaginara (elipsoidul).
Conform figurii nr.1.7.a, altitudinea elipsoidala se masoara de-a lungul normalei, N, la suprafata elipsoidului pe cand cele doua componente ale sale se masoara de, a lungul veticalei locului, V, intre aceste doua directii formandu-se unghiul de deviatie a verticale, u.
In continuare, se vor prezenta numai acele sisteme de altitudini a caror componenta principala se poate determina prin masuratori de nivelment geometric. Toate acestea au ca punct de plecare un punct de cota "0" absolut, situat la nivelul mediu al marii adica, pe suprafata echipotentiala a geoidului avand W (O) = ct.
Considerand un punct, A, situat pe suprafata fizica a Pamantului. Prin care trece suprafata echipotentiala avand W(A) = ct. se poate scrie expresia diferentei de potential dintre cele doua puncte:
dW = W(O) - W(A) = - g . dh
In
cadrul acestei relatii potentialul gravitational se noteaza cu w reprezentand o
suma a potentialelor gravitatii si fortei centrifuge. Suprafata de nivel este o
suprafata sferica care din punct de vedere matematic insa nu satisface
cerintele din punct de vedere ale preciziei masuratorilor geodezice, astfel
incat intr-o a doua aproximatie forma pamantului se identifica un sferoid de
nivel cunoscut sub numele de sferoidul Bruns, marele dezavantaj este ca
formulele matematice cel definesc sunt extrem de complexe. O solutie de
compromis este alegerea unei suprafete care pe de o parte sa aproximeze in bune
conditii forma pamantului, iar pe de o parte sa poata fi reprezentat din punct
de vedere matematic printr-o formula matematica si tot odata sa i se poata
determina valoarea potentialului si al gravitatiei. Aceasta este considerata ca
fiind forma normala a pamantului corespunzator careia avem potentialul normal U
si gravitatea normala notata cu ![]() . Diferenta
dintre potentialul normal si cel real al pamantului notat cu w se numeste
potential perturbator. Aceasta descompunere a potentialului faciliteaza
determinarea din geodezia fizica, deoarece considerand cunoscuta masa
pamantului potentialul normal se poate considera ca avand o valoare unica
astfel incat prin masuratori urmeaza sa se determine cu niste valori mici
corespunzatoare potentialului perturbator.
. Diferenta
dintre potentialul normal si cel real al pamantului notat cu w se numeste
potential perturbator. Aceasta descompunere a potentialului faciliteaza
determinarea din geodezia fizica, deoarece considerand cunoscuta masa
pamantului potentialul normal se poate considera ca avand o valoare unica
astfel incat prin masuratori urmeaza sa se determine cu niste valori mici
corespunzatoare potentialului perturbator.
In
geodezie importanta este suprafata de nivel absolut sau de nivel 0 a geoidului
cu potentialul notat cu w![]() .
.
Ecuatia
suprafetei de nivel w =
w![]() = ct.
= ct.
|
fig. 1.7.a |
fig. 1.7.b |
O suprafata de nivel poate fi definita ca fiind suprafata in a caror puncte verticala locului sau normala la geoid este perpendiculara, dar in acelasi timp poate fi definita ca locul geometric al punctelor in care aceeasi directie principala este tangenta la liniile de forta a campului grafic terestru care dupa cum se observa din figura nr. sunt indreptate cu concavitatea spre poli si nu trec prin centrul de masa al pamantului.
fig. 1.8
a. Sisteme de coordonate altimetrice
Se pot defini o multime de sisteme de coordonate altimetrice dintre care vom studia numai pe acelea a caror parte principala se poate determina prin masuratori de nivel.
Dupa cum stim toate acestea au ca origine un
punct de cota 0 situat la nivelul marilor si oceanelor adica pe geoidul de
potential (w![]() )=ct.
)=ct.
Consideram pe suprafata fizica un punct A w(A)=ct.
Diferenta de potential dintre cele doua puncte
dw = w(A) -
w(0) = ![]()
![]()
![]()

in cazul acestei relatii cu g se noteaza gravitatea reprezentand de fapt gradientul vertical negativ al potentialului gravitati masurat in sensul cresterii altitudinii
![]()
In geodezie diferenta de potential dintre doua puncte se numeste numar geopotential si se noteaza cu C avand deci expresia dw
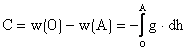
Este de interes sa exprimam cota unui punct A sub forma unei relatii ce poate fi privita ca o definitie fizica a altitudinii, preferabil o definitie geometrica
![]()
In
cadrul careia ![]() reprezinta gravitatea medie masurata de-a
lungul verticalei locului ce trece prin A. Geometric putem defini altitudinea
prin urmatoarea formula
reprezinta gravitatea medie masurata de-a
lungul verticalei locului ce trece prin A. Geometric putem defini altitudinea
prin urmatoarea formula
H
=![]()
unde F - o marime fizica dinamica in functie de care putem defini o multime de sisteme de altitudini.
1. Alitudinea dinamica
Daca inlocuim in formula generala gravitatea,
F cu ![]() ce reprezinta gravitatea normala, masurata la
o altitudine oarecare obtinem formula fizica ce exprima altitudinea dinamica:
ce reprezinta gravitatea normala, masurata la
o altitudine oarecare obtinem formula fizica ce exprima altitudinea dinamica:
![]()
Acest tip de altitudine are marele avantaj ca nu depindede drumul parcurs de nivelment.
Masurarea
sa principala o reprezinta altitudinea determinata prin nivelment geometric de
precizie la care se adauga as numita corectie dinamica notata cu ![]() astfel incat expresia diferentelor de nivel
dinamica dintre doua puncte
astfel incat expresia diferentelor de nivel
dinamica dintre doua puncte
![]()
![]()
![]()
![]()
Primul termen reprezinta diferenta de nivel obtinuta prin nivelment geometric, iar a doua parte este chiar expresia corectiei dinamice.
![]()
Diferenta de altitudine dinamica este:
![]()
Relatia poate fi utilizata pentru calculul diferentei numerelor geopotentiale:
![]()
deoarece toate marimile din partea dreapta a egalitatii sunt determinabile.
2. Altitudinea ortometrica
Pentru
F=![]() se obtine
altitudinea ortometrica:
se obtine
altitudinea ortometrica:
![]()
unde
asa cum am mai spus ![]() reprezinta gravitatea medie masurata de-a
dreptul verticalei locului V din punctul A si se poate defini printr-o relatie
de genul:
reprezinta gravitatea medie masurata de-a
dreptul verticalei locului V din punctul A si se poate defini printr-o relatie
de genul:

unde prin g(z) s-a dat gravitatea in punctul curent M si este pe verticala punctului A, la altitudinea ortometrica z.
A
![]()
fig. 1.9
Reiese ca altitudinea ortometrica are o interpretare parametrica clara, ea reprezentand constanta dintre geoid si punctul A de o suprafata fizica a Pamantului, masurata de-a lungul verticalei din A.
Aceasta relatie este utilizata mai mult pentru determinarea altitudinilor ortometrice decat ca relatie de calcul deoarece in general numerele geopotentiale nu sunt cunoscute precis. Pentru calculul practic se refera metoda corectarii rezultatelor nivelmentului geometric cu asa numita corectie ortometrica:

altitudinile dinamice ale celor doua puncte sunt:
![]() ;
; ![]()

I V![]()
![]() V
V![]()
![]()
H![]() H
H![]()
 geoid
geoid
A![]() B
B![]()
fig. 1.10
unde
H![]() si H
si H![]() sunt
altitudinile determinate prin nivelment geometric
sunt
altitudinile determinate prin nivelment geometric
![]()
expresia corectiei ortometrice este:
![]() -
-
iar pentru calculul acesteia se inlocuiesc termenii:
![]()
![]() =
valoarea medie a gravitatii de-a lungul porteei i
=
valoarea medie a gravitatii de-a lungul porteei i
![]() relatiile
medii ale gravitatii de-a lungul liniilor de forta
relatiile
medii ale gravitatii de-a lungul liniilor de forta ![]() si
si ![]()
![]() valoarea
gravitatii normale la o anumita latitudine
valoarea
gravitatii normale la o anumita latitudine
Altitudinea normala
Se
obtine inlocuind F =![]()
![]()
unde
![]() gravitatea
normala medie de-a lungul normalei la elipsoid in punctul A
gravitatea
normala medie de-a lungul normalei la elipsoid in punctul A
A(w![]() =ct)
=ct)

![]()
![]()
![]()
![]() A
A![]()
suprafata hipsometrica
 H
H![]()
A![]()
elipsoid
![]()
fig. 1.12
El
este proiectat pe suprafata elipsoidului prin normala in A![]() ea este
normala la elipsoid de potential normal
ea este
normala la elipsoid de potential normal ![]() se alege punctul A
se alege punctul A![]() al carui
potential normal U(A
al carui
potential normal U(A![]() ) sa fie
egal cu potentialul real w(A). Distanta A
) sa fie
egal cu potentialul real w(A). Distanta A![]() A
A![]() masurata
de-a lungul normalei defineste altitudinea normala a punctului A:
masurata
de-a lungul normalei defineste altitudinea normala a punctului A:![]() .
.
Daca
pentru fiecare punct M![]() de pe
suprafata fizica a Pamantului se defineste punctul corespunzator M
de pe
suprafata fizica a Pamantului se defineste punctul corespunzator M![]() ,
totalitatea acestora se vor afla pe o suprafata de nivel, denumita suprafata
hipsometrica sau telluroid. Distanta AA
,
totalitatea acestora se vor afla pe o suprafata de nivel, denumita suprafata
hipsometrica sau telluroid. Distanta AA![]() dintre suprafata fizica si suprafata trigonometrica se numeste
anomalie a inaltimi si se noteaza cu
dintre suprafata fizica si suprafata trigonometrica se numeste
anomalie a inaltimi si se noteaza cu ![]() .
.
Determinarea practica a altitudinii normale nu este posibila deoarece suprafata de referinta-elipsoidul nu este o suprafata materiala. Pentru rezolvarea problemei M.S. Molodenski (1945) a introdus o suprafata ajutatoare numita cvasigeoid.
Fiecarui
punct Mi a suprafetei pamantului ii corespunde o altitudine normala ![]() si o anomalie a inaltimi
si o anomalie a inaltimi ![]() . Daca pe
normalele HiHi0 se i-au segmentele
. Daca pe
normalele HiHi0 se i-au segmentele ![]() se obtine suprafata cvasigeoidului:
se obtine suprafata cvasigeoidului:


fig. 1.13
Din definitia cvasigeoiului rezulta doua proprietati foarte importante ale acestuia:
cvasigeoidul nu este o suprafata echipotentiala deoarece nici suprafata hipsometrica (prin intermediul careia este determinat) nu este o suprafata echipotentiala;
pe suprafata marilor si a oceanelor cvasigeoidul coincide cu geoidul.
In acest caz, numerele cvasipotentiale ale punctelor Mi vor fi 0 si ca consecinta si altitudinile normale vor fi 0.
De
aici rezulta ca altitudinile punctelor situate pe suprafata marilor masurate de
la elipsoid vor fi egale cu anomalia inaltimi deci xxxxx ![]() poate fi definita ca distanta dintre suprafata
de vizare a potentialului real W (M) si cea a potentialului normal U(M) pentru
un punct.
poate fi definita ca distanta dintre suprafata
de vizare a potentialului real W (M) si cea a potentialului normal U(M) pentru
un punct.
![]()
W(M)
= W(0)- ; U(M) = U(0)-
; U(M) = U(0)-
Unde 0 este punctul initial al nivelmentului situat la nivelul marii. Introducerea cvasigeoidului da posibilitatea obtinerii altitudinii normale ca suma a doua componente:
HN
= Hmas + ![]()
Hmas = altitudinea masurata prin nivelment geometric
![]() = corelatia normala
= corelatia normala
Relatia de definire a altitudinii normale
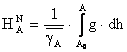
A = puncte pe suprafata fizica
A0 = puncte pe elipsoid
![]() = valoarea medie a gravitatiei de-a lungul
normalei intre A si A0 suprafetele de nivel folosite in geodezia
fizica:
= valoarea medie a gravitatiei de-a lungul
normalei intre A si A0 suprafetele de nivel folosite in geodezia
fizica:


fig. 1.14
4. Ecuatii parametrice ale elipsoidului de referinta
Ecuatia generala a unui elipsoid de referinta, exprimata sub forma implicita este:
![]()
In afara de aceasta ne intereseaza sa determinam si alte relatii care sa
faca legatura dintre coordonatele carteziene tridimensionale X, Y, Z si
coordonatele geografico-geodezice ![]() , de exemplu ale unui punct S, exprimabile fata
de parametrii elipsoidului (motiv pentru care se mai numesc ecuatii parametrice).
Conform figurii de mai jos, legatura dintre acestea este urmatoarea:
, de exemplu ale unui punct S, exprimabile fata
de parametrii elipsoidului (motiv pentru care se mai numesc ecuatii parametrice).
Conform figurii de mai jos, legatura dintre acestea este urmatoarea:
X = x(![]() );
);
Y = y(![]() );
);
Z = z(![]() )
)


fig. 1.15
Pentru obtinerea acestora trebuie insa sa determinam ecuatiile parametrice ale elipsei meridiene. In figura de mai jos sectiunea meridiana a punctului S contine un sistem cartezian bidimensional de coordonate x, z ambele exprimabile in functie de latitudinea geografica-geodezica: x = x(φ), z = z(φ)
Din studiul celor doua figuri se observa imediat legatura dintre cele doua sisteme de coordonate:
X = x cos![]()
Y = y sin![]()
Z = z.


fig. 1.16
In acest sistem de coordonate
ecuatia elipsei meridiane scrisa sub forma implicita va fi: f(x,z) = ![]() +
+![]()
In cadrul acesteia inlocuim pe b2 = a2(1- e2) si inmultind termenii relatiei cu a2 obtinem:
f(x,z) = x2 +
![]() - a2 =0
- a2 =0
Diferentiind total aceasta functie obtinem:

dar ![]() si
si ![]()
![]()
si prin urmare: 
Din studiul figurii, acest raport reprezinta din punct de vedere geometric panta tangentei la curba.
![]() = tg (90o
+
= tg (90o
+ ![]() ) = -ctg
) = -ctg![]() = -
= - ![]()
![]() = -
= -![]() =
=![]() z =
z = ![]()
Inlocuind in functia noastra initiala vom obtine:

Procedand in mod analog, obtinem:
![]()
Inlocuind in functia noastra initiala vom obtine:
 +
+ ![]() = a2
= a2
![]()
 = a2
= a2 ![]()
 = a2
= a2 ![]()
 = a2
= a2![]()
z2(1-e2sin2![]() = a2e2(1-e2)2sin2
= a2e2(1-e2)2sin2![]()
![]()
z = 
Tinand cont de aceste rezultate vom obtine ecuatiile parametrice ale elipsoidului de rotatie:
X = ![]()
Y = ![]()
Z = 
In geodezie si proiectii cartografice datorita complexitatii calculelor o serie de coeficienti variabili cu latitudinea si exprimabili in functie de parametrii elipsoidului de referinta denumiti si coeficienti auxiliari, au primit niste notatii si sunt calculati in functie de latitudine si intabelati in asa numitele tabele ale elipsoidului.
Coeficientii sunt:
W = ![]() ; V =
; V = ![]() =
= ![]()
![]() e'2cos2
e'2cos2![]() ; t
= tg
; t
= tg![]() =
= ![]()
Daca ne propunem sa stabilim niste relatii intre coeficientii auxiliari W, V procedam astfel:
W = 1 - e2sin2![]() dar e2 =
dar e2 = ![]()
![]()
![]()
![]()
![]()
![]() =
=
=![]() =
=![]()
![]()
![]()
![]()
Ne propunem sa exprimam ecuatiile parametrice si in functie de parametrul
auxiliar V. Pentru aceasta preluam raportul ![]() si-l exprimam la patrat
si-l exprimam la patrat

![]()
![]()
![]()
![]()
In concluzie, ecuatiilor parametrice ale elipsoidului de rotatie, exprimate in functie de cei doi parametri auxiliari sunt urmatoarele:
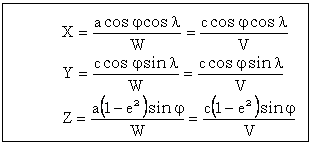
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 6536
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved