ELEMENTELE SFEREI SI ELIPSOIDULUI TERESTRU

ELEMENTELE SFEREI SI ELIPSOIDULUI TERESTRU

In fig.5 si fig.6 sunt reprezentate in perspectiva modelele sferic, respectiv elipsoidal ale Pamantului. Pentru ambele modele matematice se definesc urmatoarele elemente comune ale acestora :

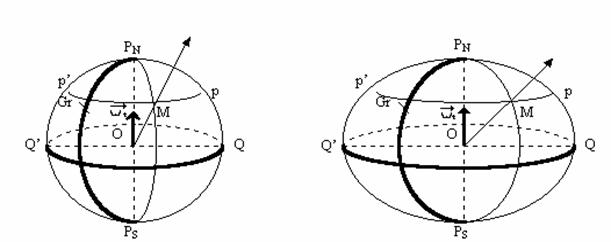
[ Fig.5 ] Sfera terestra Fig.6 ] Elipsoidul terestru

O , centrul sferei (elipsoidului) ;

M , punct oarecare pe suprafata sferei (elipsoidului) ;

axa P_NP_{S ,} axa de rotatie a Pamantului, numita si axa polilor; vectorul este vectorul viteza unghiulara de rotatie a Pamantului in jurul axei polilor;

P_N , P_S , polul nord terestru, respectiv polul sud terestru, puncte in care axa polilor inteapa sfera (elipsoidul) ;

cercurile mari, sunt cercuri pe suprafata sferei terestre, ale caror plane contin centrul sferei; cercurile mici, sunt cercuri ale caror plane nu contin centrul sferei. Cercurile mari au raza egala cu raza sferei terestre, in timp ce cercurile mici au razele mai mici decat raza sferei terestre;

planele axiale, plane care contin axa polilor ;

planul ecuatorului, plan perpendicular pe axa polilor care contine centrul sferei (elipsoidului). Acesta imparte sfera terestra in doua emisfere : emisfera nordica este emisfera care contine polul nord geografic iar emisfera sudica este emisfera care contine polul sud geografic;

ecuatorul terestru, este cercul mare pe suprafata sferei (elipsoidului), rezultat din intersectia planului ecuatorului cu sfera, respectiv cu elipsoidul (se noteaza cu QQ');

meridianele sunt semicercuri mari de la un pol la celalalt. Meridianele rezulta din intersectia planelor axiale cu sfera, respectiv cu elipsoidul; pe sfera, meridianele sunt semicercuri, iar pe elipsoid sunt jumatati de elipse. S-a ales ca meridian origine, meridianul care trece prin centrul optic al instrumentului meridian al observatorului astronomic Greenwich (the Old Greenwich Astronomical Observatory). Acest meridian se numeste meridianul Greenwich, primul meridian sau meridianul zero; el imparte sfera terestra in doua emisfere: emisfera estica si emisfera vestica. In navigatie se opereaza des cu notiunea de antimeridian al unui meridian. Spre exemplu, daca se face referire la meridianul de 030E, atunci antimeridianul acestuia este meridianul de 150W. In mod identic, atunci cand se face referire la meridianul Greenwich, atunci se va intelege ca antimeridianul lui este meridianul de 180 (acesta se mai numeste si meridianul de schimbare a datei);

paralelele sunt cercuri mici ce rezulta din intersectia sferei (elipsoidului) cu plane paralele cu planul ecuatorului.

Ca urmare, prin orice punct de pe suprafata sferei (elipsoidului) trec un meridian si un paralel. Se definesc deci, pe sfera terestra, o infinitate de meridiane si, respectiv, de paralele;

Verticala unui punct oarecare M este dreapta determinata de centrul O al sferei (elipsoidului) si punctul M (se aproximeaza faptul ca centrul sferei/elipsoidului coincide cu centrul de masa al Pamantului, numit si geocentru). Segmentul OM se numeste raza sferei terestre (R) pe sfera, respectiv raza vectoare geocentrica (r) pe elipsoid. Pe sectiunea meridiana a sferei terestre trasata prin punctul M (fig.7) se poate evidentia cu usurinta faptul ca verticala punctului M este perpendiculara la tangenta (TT') dusa la cercul meridian, si deci coincide cu normala. In fig.8, in care s-a reprezentat sectiunea meridiana a elipsoidului dusa prin punctul ales M, se poate observa ca raza vectoare geocentrica (OM = r) nu este perpendiculara pe tangenta TT' la elipsa meridiana. Pe elipsoid, normala (N) a unui punct nu coincide cu verticala sa (V).

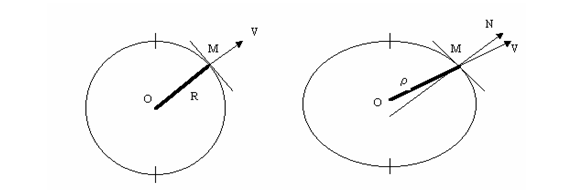
Fig.7 Sectiunea meridiana [Fig.8] Sectiunea meridiana

a sferei terestre a elipsoidului