FORMA PAMANTULUI.

Asa cum se poate lesne constata, forma reala a Pamantului este absolut neregulata, imposibil de modelat matematic in mod fidel. Ca urmare a acestui fapt, atentia oamenilor de stiinta, in special a geodezilor, s-a concentrat asupra problemei aproximarii formei reale a Pamantului cu un corp geometric, care sa fie regulat si care sa nu se indeparteze foarte mult de figura reala, neregulata, a Pamantului.

Exista in principiu doua posibilitati de aproximare a formei (figurii) Pamantului: aproximarea fizica si aproximarea matematica.

Corpul care aproximeaza fizic Pamantul se numeste GEOID. Acesta este corpul care are suprafata data de suprafata linistita a marilor si oceanelor Pamantului, prelungita pe sub continente. In consecinta, geoidul nu ia in considerare formele nesemnificative de relief.

O alta maniera de definire a geoidului face apel la notiuni de teoria potentialului. Astfel, se defineste potentialul unei forte, ca fiind functia ale carei derivate partiale pe axele de coordonate sunt chiar proiectiile fortei pe axe. Multimea punctelor din spatiul R₃ care au acelasi potential, definesc o suprafata echipotentiala. Daca forta in cauza este forta gravitatii (se mai numeste si greutate, si este suma dintre forta efectiva de atractie a Pamantului si forta centrifuga), atunci potentialul sau se numeste potentialul gravitatii.

In acest context, geoidul se defineste ca fiind corpul avand suprafata echipotentiala de nivel zero (nivelul mediu al marilor si oceanelor). Aceasta definitie a fost introdusa de Listing in anul 1873, si a fost propusa, ulterior, de Gauss, ca figura a Pamantului.

Verticala unui punct este directia firului cu plumb, si este dreapta definita de acel punct si centrul de masa al Pamantului. Altfel, verticala unui punct este definita ca fiind directia gradientului functiei potential. In consecinta, verticala oricarui punct de la suprafata Pamantului este perpendiculara pe geoid (ca o consecinta a definitiei notiunii de gradient)-fig.4.

Urmare a distributiei nesferice (neomogene) a densitatii Pamantului, suprafata geoidului nu este regulata; in consecinta, utilizarea geoidului ca suprafata de referinta, la care sa se reduca toate masuratorile geodezice ori de navigatie, este restrictiva.

Din acest considerent, a fost necesara o a doua aproximatie a formei Pamantului. Aceasta este legata de numele lui Newton, care in anul 1687 fundamenteaza teoria asupra atractiei universale, pe baza careia postuleaza doua concluzii extrem de importante :

1) Forma de echilibru a Pamantului este reprezentata de un elipsoid de rotatie cu turtire mica la poli. Valoarea data de Newton turtirii a fost de 1/230) ;

2) Gravitatia (greutatea) creste de la ecuator catre poli.

Newton a demonstrat aceste afirmatii pe baza masuratorilor precise ale timpului cu ajutorul pendulului (acesta ramane in urma daca este plasat la ecuator, urmare a gravitatii scazute). Ulterior, expeditiile efectuate in Lapland si Peru (1736-1744) pentru masurarea arcelor de meridian, au confirmat ipotezele lui Newton.

Doua sute de ani mai tarziu, odata cu lansarea satelitilor artificiali ai Pamantului, s-au putut verifica din nou aceste ipoteze. Mai mult, lansarea satelitului Vanguard 1 la 17 martie 1958, a facut posibila determinarea faptului ca Pamantul are forma 'de para', polul sud fiind mai apropiat de centrul Pamantului decat polul nord cu cca. 20 km. De asemenea, s-a determinat faptul ca Pamantul contine o deformare (un bulb) la sud de ecuator (Smith J.,R.,1988).

In concluzie, in a doua aproximatie, Pamantul se asimileaza unui elipsoid de revolutie, obtinut prin rotatia elipsei meridiane in jurul axei mici (2b), numita si axa polara (fig.3). Dreapta N care trece prin punctul oarecare M si este perpendiculara pe suprafata elipsoidului, se numeste normala la elipsoid.

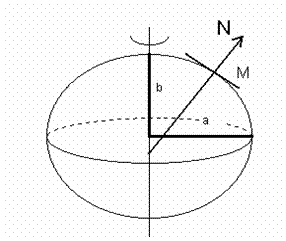
[Fig.3 ] Elipsoidul de revolutie

Parametrii elipsoidului de revolutie sunt:

semiaxa mare (ecuatoriala) a ;

semiaxa mica (polara) b ;

prima turtire f = 1-b/a .

Se definesc urmatorii parametri secundari ai elipsoidului :

prima excentricitate e = (1 - b2/a2)1/2 ;

raza de curbura polara c = a/b2.

Pe baza unor determinari astronomo-geodezice si satelitare precise, s-au determinat urmatoarele modele elipsoidale (figuri matematice) ale Pamantului, numite elipsoizi de referinta:

OBSERVATIE : WGS = World Geodetic System ;

UAI = Uniunea Astronomica Internationala.   

In fig.4 este reprezentata suprafata reala a Pamantului, pe care s-au ales doua puncte arbitrare M si M . Sunt reprezentate de asemenea suprafata geoidului (cu verticala locului V) si suprafata elipsoidului de revolutie (cu normala N).

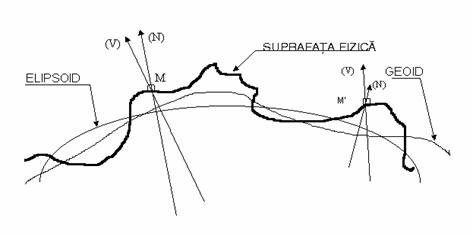
[Fig.4 ] Suprafata fizica, geoid, elipsoid

Pentru a rezolva expeditiv anumite probleme practice ale navigatiei, s-a adoptat (intr-o a treia aproximatie) ca model matematic al Pamantului, sfera. Desi mai putin precis decat modelul elipsoidal, modelul sferic al Pamantului satisface majoritatea necesitatilor navigatiei. Asimilarea elipsoidului terestru cu sfera terestra se face pe considerentul ca diferentele intre cele doua suprafete sunt, la nivelul de precizie impus de unele probleme ale navigatiei, acceptabile. De exemplu, indicarea distantelor parcurse de nava (cu aparatura de bord) este afectata de o eroare de 1%; in acelasi timp, eroarea introdusa de aproximarea suprafetei sferice a Pamantului nu depaseste procentul de 1% in determinarea acelorasi distante. Ca urmare, acest nivel de precizie se considera a fi satisfacator.

Sfera terestra se defineste ca fiind sfera cu volumul egal cu cel al elipsoidului de referinta, ales ca model matematic al Pamantului. Pornind de la aceasta egalitate, se poate determina raza sferei terestre (avand ca model elipsoidul Hayford, numit si elipsoid international):

4pR³/3 = 4pa²b/3    T R = (a²b)^1/3 = 6371.1 km (4)