Circuite electrice În curent alternativ sinusoidal

CIRCUITE ELECTRICE ÎN CURENT ALTERNATIV SINUSOIDAL

1 Marimi alternative sinusoidale. Generalitati

Se numeste marime sinusoidala sau armonica o marime alternativa, (de exemplu, curentul electric), reprezentata în figura 1, care poate fi scrisa sub forma:

i(t) = I_m sin(w t j

unde: I_m este valoarea maxima (de vârf) sau amplitudinea, w este pulsatia, iar j este faza initiala a marimii sinusoidale. Argumentul sinusului, adica marimea liniar variabila în timp  (w t j), se numeste faza marimii sinusoidale. Convenim sa numim valoare instantanee, valoarea i pe care o are marimea variabila la un moment oarecare t. Cel mai scurt interval de timp dupa care marimea periodica îsi reia valoarea în aceeasi ordine se numeste perioada, notata cu (T), având ca unitate de masura secunda.

Numarul de perioade cuprinse în unitatea de timp se numeste frecventa (f), iar produsul 2 p f = w se numeste pulsatia sau viteza de rotatie a marimii periodice, si se masoara în rad/s sau s^-1. Exista deci relatiile:

f = ; w = 2 p f = ; w T = 2 p

Frecventa se masoara în hertz (Hz).

În sistemul de unitati SI, faza si faza initiala, care sunt unghiuri, se masoara în radiani. Produsul w t = a reprezinta un unghi geometric, adica este o marime spatiala.

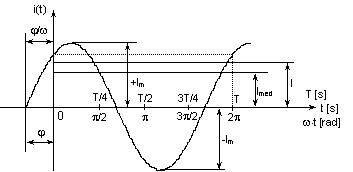
Fig. 1

Din figura anterioara, se poate observa ca funtia sinus are perioada 2 p, fapt ce face ca modificarea fazei initiale cu un multiplu pozitiv sau negativ de 2 p, sa nu modifice valoarea functiei.

Valoarea de vârf sau amplitudinea unei marimi sinusoidale, este cea mai mare valoare instantanee (ca modul) pe care o poate avea acea marime în decursul unei perioade. Aceasta valoare se noteaza, de exemplu în cazul unui curent i(t), cu simbolul I_m.

Diferenta dintre fazele initiale ale doua marimi sinusoidale se numeste defazaj. Pentru doua marimi sinusoidale de forma: i₁ = I₁ sin(w t+j₁) si i₂ = I₂ sin(w t+j₂), defazajul este:

j₁₂ j₁ j₂

Acest defazaj poate fi pozitiv sau negativ. Daca j₁ j₂ > 0, i₁ este defazat înaintea lui i₂ , ca si în figura 2,a, iar daca j₁ j₂ < 0, i₁ este defazat în urma lui i₂, ca în figura 2,b.

În cazul defazajului dintre doua marimi sinusoidale se pot ivi urmatoarele cazuri particulare:

j₁₂ j₁ j₂ = 0 marimile sunt în faza – când ambele marimi trec deodata prin zero si prin maxime, ambele marimi sunt în acelasi moment maxime pozitiv sau negativ,ele fiind sinfazice.

Sunt prezentate mai jos graficele de variatie în timp pentru o tensiune si un curent care sunt în faza.

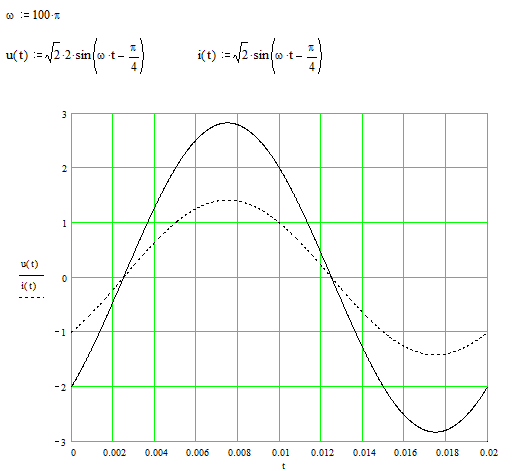
j₁₂ j₁ j₂ marimile sunt în cuadratura – când una dintre marimi trece prin maxim, cealalta trece prin zero.

j₁₂ j₁ j₂ p - marimile sunt în opozitie de faza sau în antifaza – când cele doua marimi trec deodata prin zero si prin maxime, dar acestea sunt opuse. În graficele de mai jos tensiunea u(t) este în cuadratura cu fiecare din curentii i1(t) si i2(t), în schimb cei doi curenti sunt în antifaza.

2 Valori caracteristice ale marimilor alternative sinusoidale

Valoarea medie

Valoarea medie a unei marimi variabile este data de relatia:

Fie un curent alternativ sinusoidal:

Asa cum se stie, valoarea medie a unei marimi sinusoidale, luând ca domeniu de integrare o perioada, este nula. În electrotehnica, se utilizeaza totusi, pentru caracterizarea marimilor sinusoidale, o valoare medie calculata numai pentru alternanta pozitiva, adica pentru o jumatate de perioada, exprimata cu ajutorul valorii de vârf astfel:

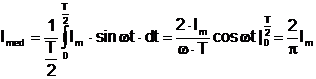= 0,636 I_m

Prin analogie se obtine valoarea medie pentru tensiune : U_med = = 0,637 U_m

Importanta valoriilor medii ale curentului si tensiunii consta în faptul ca acestea intervin la redresarea marimilor alternative sinusoidale. Aceste valori se masoara cu ajutorul aparatelor electrice de tip magnetoelectric prevazute cu redresor.

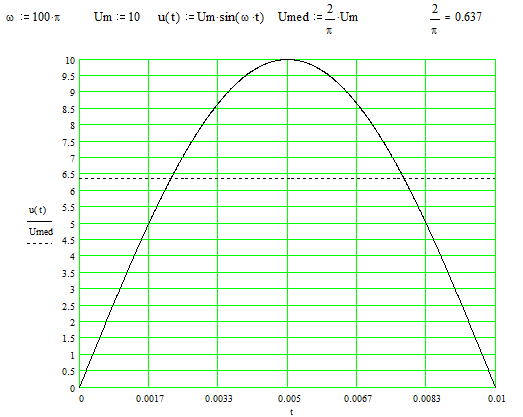
Semnificatia geometrica a valorii medii este aceea ca aria dreptunghiului marginit de valoarea medie si abscisa este egala cu aria suprafetei marginita de semialternanta pozitiva a sinusoidei si abscisa. În figura de mai sus s-a reprezentat semialternanta pozitiva a unei tensiuni sinusoidale de frecventa f = 50 Hz, T = 0.02 sec, amplitudine U_m = 10 V împreuna cu valoarea medie U_med. Faza initiala a tensiunii s-a considerat nula.

Valoarea efectiva (eficace) a unei marimi alternative sinusoidale.

Valoarea efectiva a curentului sinusoidal este egala cu acea valoare constanta I a unui curent continuu, care trecând printr-un rezistor cu rezistenta R dezvolta în timp de o perioada T aceeasi energie calorica Q ca si curentul sinusoidal i = I_m sinw t ce trece prin acelasi rezistor, în acelasi interval de timp :

Q = R I² T = 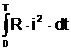 . > I = 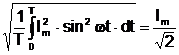= 0,707 I_m

Pentru integrare s-a folosit transformarea trigonometrica:

sin²α = (1- cos 2 α ) / 2

Prin analogie se obtine valoarea efectiva U, a unei tesiuni sinusoidale: U = = 0,707 U_m.

Valoarea efectiva a marimilor alternative sinusoidale are semnificatii importante în practica. Valoarea efectiva este indicata de aparatele electrice de masurat, pentru curentul alternativ (cu exceptia celor cu redresor).

În electrotehnica, se opereaza cu valorile efective ale marimilor sinusoidale, astfel ca se prefera pentru o marime alternativa sinusoidala scrierea sub forma:

i = I sin(w t+j

Aceasta relatie se numeste forma normala în sinus a unei marimi sinusoidale.

O marime sinusoidala este deci complet determinata daca i se cunosc valoarea efectiva I, pulsatia w, adica frecventa f, si faza initiala j

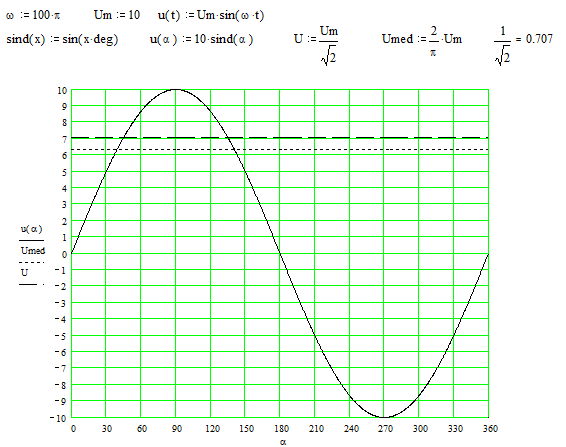
În figura de mai sus s-a reprezentat varaitia tensiunii sinusoidale u(t) împreuna cu valoarea medie si cea efectiva. În abscisa s-a reprezentat marimea ωt exprimata în grade.