Tehnici de modelare utilizate În planificarea si validarea miscarii nominale a robotilor

TEHNICI DE MODELARE UTILIZATE ÎN PLANIFICAREA SI VALIDAREA MISCARII NOMINALE A ROBOTILOR

1.1 MODELUL GEOMETRIC DIRECT

Cea mai mare parte a cinematicii robotilor se ocupa cu stabilirea diferitelor sisteme de coordonate ce permit determinarea pozitiilor si a orientarii corpurilor rigide si cu determinarea transformarilor care au loc între aceste sisteme. Geometria spatiului tridimensional si miscarea rigida, joaca un rol central  în toate aspectele legate de sistemele robot. În acest capitol vor fi studiate operatiile de rotatie si de translatie si se va introduce notiunea de transformare omogena, care combina cele doua operatii într-o singura matrice si care conduce la stabilirea ecuatiilor cinematice directe ale unui robot manipulator.

Scopul acestui capitol este de a prezenta o metodologie ce permite determinarea pozitiei (coordonatelor carteziene) si a orientarii efectorului fata de baza, în functie de valorile variabilelor generalizate atasate articulatiilor.

1.1.1 Matricea de transformare de orientare (matricea de rotatie)

Figura 1.1.1

Daca consideram doua sisteme de coodonate X₀Y₀Z₀ si X₁Y₁Z₁, cu aceeasi origine O si un punct P din spatiu, putem scrie coordonatele punctului P fata de cele doua sisteme de coordonate sub forma (figura 1.1.1)

(1.1.1) , unde

i, j, k sunt versorii unitari asociati respectiv axelor de coordonate X, Y, Z.

Înmultind ecuatia (1.1.1) pe rând cu i₁, j₁, si k₁ obtinem un sistem de ecuatii care matricial se scrie sub forma :

(1.1.2) , unde

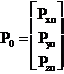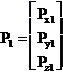  reprezinta coordonatele punctului P fata de sistemul “0” reprezinta coordonatele punctului P fata de sistemul “1”, ,iar matricea 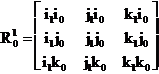(1.1.3) 

reprezinta matricea de transformare de coordonate de “orientare” (sau matricea de rotatie) a sistemului “1” fata de sistemul “0”. Semnificatia coloanelor matricei de rotatie (1.1.3) este urmatoarea : coloana 1 reprezinta proiectiile versorului i₁ în sistemul de coordonate “0” (i₁i₀, i₁j₀, i₁k₀), coloana 2 reprezinta proiectiile versorului j₁ în sistemul de coordonate “0” (j₁i₀, j₁j₀, j₁k₀), iar coloana 3 reprezinta proiectiile versorului k₁ în sistemul de coordonate “0” (k₁i₀, k₁j₀, k₁k₀) (înmultirea dintre versori fiind evident înmultire vectoriala).

În plus matricea de rotatie (1.1.3) are si urmatoarea proprietate :

(1.1.4)

adica inversa, matricea de trecere de la sistemul “0” la sistemul “1”, se

obtine prin transpunere. Acest lucru devine transparent tinând cont de semnificatia coloanelor matricii inverse , în care de exemplu coloana 1 reprezinta proiectiile versorului i₀ în spatiul de coordonate “1” (i₀i₁, i₀j₁, i₀k₁) si care este identica cu linia 1 a matricii .

Regula de compunere a matricilor de rotatie

Daca în plus fata de sistemul de baza “0” si de sistemul “1” considerat (numit si sistem curent), sisteme legate prin matricea de rotatie , consideram  un al treilea sistem “2”, având originea comuna cu celelalte doua, dar care s-a obtinut printr-o rotatie cu fata de sistemul curent, atunci postmultiplicând cu obtinem , adica matricea de rotatie a sistemului “2” fata de sistemul de baza “0”.

Daca cea de-a doua rotatie este realizata fata de sistemul de baza, atunci premultiplicând cu obtinem , adica matricea de rotatie a sistemului “2” fata de sistemul de baza “0”. În cazul sistemelor cu roboti, în general rotatia se face fata de sistemul curent, deci matricea rezultanta se obtine prin postmultiplicare.

Daca consideram un numar de sisteme de coordonate având aceeasi origine O, matricea de transformare de coordonare de orientare de la sistemul “k” la sistemul “q” (q<k) în mod general se scrie :

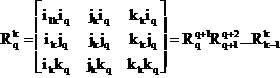.(1.1.5)

1.1.2 Unghiurile lui Euler

O matrice de rotatie poate fi exprimata si ca produsul  unor rotatii succesive în jurul axelor principale, luate într-o ordine specificata. Aceste rotatii definesc unghiurile yaw (rostogolire), pitch (tangaj) si roll (rostogolire), numite în literatura “unghiurile lui Euler”.

Matricea de rotatie în jurul axei Z este (1.1.6),

Figura 1.1.2

unde s-a introdus notatia pentru , respectiv pentru .

Figura 1.1.3

Matricea de rotatie în jurul axei Y este (1.1.7)

Figura 1.1.4

Matricea de rotatie în jurul axei X este :

(1.1.8)

Matricea de transformare la sfirsitul celor trei rotatii este :

(1.1.9)

Ordinea în care se fac cele trei rotatii (1.1.6), (1.1.7) si (1.1.8), este determinanta pentru rezultatul final. De exemplu o rotatie cu y în jurul lui Z₀, urmata de o rotatie cu r în jurul lui Y₁ nu este egala cu o rotatie cu r în jurul lui Y₀, urmata de o rotatie cu y în jurul lui Z₁ :

.

1.1.3 Matricea de transformare de coordonate de configurare (matricea de transformare omogena)

Daca sistemele de coordonate nu au aceeasi origine (cum va fi de altfel cazul în sistemele cu roboti) se introduce o matrice care sa cuprinda informatii atât despre orientarea punctului P cât si despre deplasarea lui fata de originea O.

Figura 1.1.5

X0

Folosind rationamentul anterior (relatia (1.1.2)), putem scrie si conform figurii , deci , unde reprezinta distanta de la O₁ pâna la O₀, exprimata fata de sistemul “0”. Aceasta ultima relatie se poate scrie sub forma matriciala:

sau (1.1.10)

unde (1.1.11) reprezinta

matricea de tranformare de coordonate “de configurare” din sistemul “1” în sistemul “0”numita si matricea de transformare omogena.

Generalizând, putem scrie ca pentru q<k matricea de tranformare de coordonate “de configurare” din sistemul “k” în sistemul “q” este :

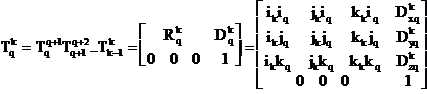(1.1.12)

Spre deosebire de cazul anterior, matricea inversa, care da orientarea si pozitia sistemului “q” fata de sistemul “k” are acum o forma mai complexa

(1.1.13)

Folosind relatia (1.1.13) se poate deduce o relatie de legatura între distanta dintre cele doua sisteme, exprimata în sistemele “k” si respectiv “q” si anume :

(1.1.14)

1.1.4 Sistemul de coordonate Denavit-Hartenberg (D-H)

Din punct de vedere al analizei cinematice a unui sistem robot, ne putem gândi ca acesta este format dintr-un set de bratele rigide, conectate între ele prin diferite articulatii. Aceste articulatii pot fi foarte simple, cum sunt articulatiile de rotatie si articulatiile de translatie sau pot fi ceva mai complexe. Diferenta este ca în cazul simplu, articulatiile au doar un singur grad de libertate a miscarii, unghiul de rotatie pentru articulatiile de rotatie si valoarea deplasarii liniare în cazul articulatiilor prismatice. În continuare se vor studia numai aceste tipuri simple de articulatii. Scopul analizei cinematicii directe este de a determina cumularea efectelor întregului set de variabile, asociate articulatiilor. Desi, este posibil sa se deduca modelul geometric direct al unui robot folosind sisteme de coordonate arbitrar asociate articulatiilor unui robot, este util sa se sistematizeze alegerea acestor sisteme de coordonate. O conventie de alegere a acestor sisteme foarte des întâlnita în aplicatiile cu roboti este conventia Denavit-Hartenberg.

În cadrul acestei formulari, trecerea de la un sistem de coordonate la altul se face printr-o succesiune de patru transformari distincte: o rotatie si o translatie în jurul axei X, urmata de o rotatie si o translatie în jurul axei Z, sau a doua varianta în care succesiunea este inversa o rotatie si o translatie în jurul axei Z, urmata de o rotatie si o translatie în jurul axei X. Astfel, în functie de ordinea axelor în jurul carora se realizeaza cele doua miscari posibile, X urmata de Z sau Z urmata de X, putem spune ca exista doua metode de stabilire a matricilor omogene de transformare, care difera prin modul de alocare a sistemelor de coordonate atasate articulatiilor si a parametrilor asociati.

1.1.5 Prima metoda de alocare a sistemelor de coordonate conform formalismului D-H

Prima metoda de alocare a sistemelor de coordonate este prezentata în figura 1.1.6

Figura 1.1.6

În aceasta conventie matricea de transformare omogena de la sistemul “i” la sistemul “i-1” notata cu reprezinta rezultatul celor patru transformari si anume :

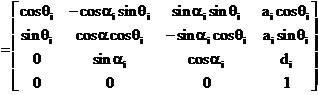(1.1.15)

unde cei patru parametri q_i,, a_i,, d_i,, a_i, reprezinta parametri Denavit-Hartenberg asociati  bratului “i”.

Aceasta abordare presupune îndeplinirea a doua conditii ce asigura unicitatea matricii de transformare omogena de la sistemul “i” la

sistemul “i-1” :

(DH1) axa x_i sa fie perpendiculara pe axa z_i-1

(DH2) axa x_i sa intersecteze axa z_i-1

Respectându-se aceste conditii exista un set unic de parametrii a, d, q a astfel încât :

(1.1.16)

Pentru a arata ca matricea Tⁱ_i-1 poate fi scrisa în mod unic sub aceasta forma (1.1.15), se pleaca de la scrierea generala :

(1.1.17)

Cele doua ipoteze (DH1) si (DH2) sunt reprezentate în figura 1.1.7

Figura 1.1.7

Conform ipotezei (DH1) vectorul r₁ (prima coloana a matricei R, care reprezinta proiectia lui i₁ în sistemul “0”) este ortogonal cu vectorul k₀=[0 0 1]^T, de unde rezulta ca r₃₁=0. În continuare trebuie sa aratam ca exista doua unghiuri unice q si a (între 0 si 2p) astfel încât :

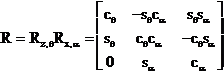(1.1.18)

Deoarece coloanele lui R sunt ortonormate, iar r₃₁=0 rezulta ca :

r₁₁²+r₂₁²=1, r₃₂²+r₃₃²=1(1.1.19)

Relatiile (19) conduc la valori unice pentru q si a astfel încât :

(r₁₁,r₂₁)=(c_q,s_q) si (r₃₃,r₃₂)=(c_a,s_a (1.1.20)

Odata gasite valorile lui q si a, este usor de verificat ca elementele ramase din matricea R corespund formei (18), folosind faptul ca matricea R este o matrice de rotatie.

Ipoteza (DH2) înseamna ca vectorul d=d₀¹ (vectorul de coordonate al originii sistemului “1” exprimat în coordonatele sistemului “0”) este o combinatie liniara între k₀ si Ri₁.

Deoarece r₃₁=0 putem exprima în mod unic :

d₀¹=dk₀+aRi₁=dk₀+ar₁= (1.1.21)

Substituind R conform (1.1.18) si d conform (1.1.21) în relatia (1.1.17), obtinem matricea de transformare omogena conforn (1.1.16).

Ceea ce s-a discutat anterior reprezinta semnificatiile logice si conditiile necesare aplicarii formalismului Denavit-Hartenberg si a alegerii parametrilor. În plus se pot desprinde si semnificatii fizice ale parametrilor si anume:

- a reprezinta distanta dintre axele z₀ si z₁, masurata de-a lungul lui x₁,

- unghiul a este masurat într-un plan perpendicular pe x₁ între axele z₀ si z₁,

- parametrul d reprezinta distanta între O₀ si intersectia lui x₁ cu axa z₀ masurata de-a lungul lui z₀

- unghiul q reprezinta unghiul dintre x₀ si x₁ masurat într-un plan perpendicular pe axa z₀.

Se poate arata ca pentru un sistem manipulator se pot alege întotdeauna sistemele de coordonate 0, 1,..n în asa fel încât sa se respecte cele doua ipoteze (DH1) si (DH2), în conditiile în care se accepta posibilitatea ca sistemul “i” sa nu apartina în unele situatii articulatiei “i”.

La început se indentifica toate axele z₀, z₁, z_n.unde z_i este axa de rotatie pentru articulatia i, daca aceasta este de revolutie si axa z_i este axa de translatie daca articulatia i este prismatica.

Se alege originea O₀, care poate fi aleasa oriunde de-a lungul lui z₀. În continuare se aleg axele x₀ si y₀, arbitrar, cu conditia ca împreuna cu z₀ sa formeze un sistem de coordonate cartezian.

Presupunem ca s-au stabilit sistemele 0, 1, i-1. În alegerea sistemului “i” pot aparea urmatoarele cazuri (a) axele z_i-1, z_i nu sunt coplanare si (b) axele z_i-1, z_i sunt coplanare. Daca axele z_i-1, z_i nu sunt coplanare, atunci exista un unic segment perpendicular pe amândoua si de lungime minima. Acest segment îl va defini pe x_i si punctul de intersectie cu z_i va defini originea O_i. Atunci prin constructie ambele conditii (DH1) si (DH2) sunt îndeplinite si vectorul de la O_i-1 la O_i este o combinatie liniara între z_i-1 si x_i. Specificarea sistemului O_i este completata prin alegerea lui y_i în asa fel încât sa se obtina un sistem cartezian.

Daca axele z_i-1, z_i sunt coplanare, atunci ele fie sunt paralele, fie se intersecteaza. Daca sunt paralele, atunci exista o infinitate de normale comune celor doua axe si conditia (DH1) nu specifica în mod unic alegerea lui x_i. În acest caz alegem originea O_i în articulatia “i” în asa fel încât x_i este cea normala la z_i-1 care trece prin O_i. Alegerea lui O_i este arbitrara în acest caz, se poate alege x_i ca fiind si normala care trece prin O_i-1, caz în care diatanta d_i este egala cu 0. Cum axele z_i-1, z_i sunt paralele, unghiul a_i este 0. Dupa ce a fost ales x_i, y_i se alege cu singura conditie sa completeze sistemul.

Daca axele z_i-1, z_i se intersecteaza, axa x_i este aleasa perpendiculara pe planul format de z_i-1, z_i. Directia pozitiva este arbitrara. Cea mai des întâlnita alegere a punctului O_i este la intersectia celor doua axe, dar se poate alege orice punct convenabil de-a lungul lui z_i. În acest caz parametrul a_i este egal cu 0.

Pentru a se completa constructia este necesar sa se aleaga sistemul de coordonate n. Originea O_n este de obicei aleasa simetric fata de “degetele” efectorului. Vectorii unitari ai axelor x_n, y_n, z_n se noteaza cu n, s, a (figura nr 1.1.8). Terminologia vine de la faptul ca directia a este directia de apropiere (approach) a efectorului fata de obiect, directia s este directia de-a lungul careia se misca (sliding) degetele efectorului în sensul de deschidere si închidere a griparului, iar directia n (normal) este directia normala pe planul format de s si a.

Figura nr 1.1.8

Regulile folosite sunt urmatoarele:

Se stabilesc articulatiile si axele de miscare z₀, z₁, .z_n-1.

Se stabileste sistemul de coordonate de baza. Se alege originea O₀ oriunde de-a lungul axei z₀. Axele x₀ si y₀ se aleg arbitrar în asa fel încât sa formeze un sistem de coordonate cartezian.

Pentru i=1,n-1 se parcurg iterativ urmatorii pasi:

Se stabileste originea O_i în punctul în care normala comuna la z_i-1 si z_i intersecteaza axa z_i. Daca z_i-1 si z_i se intersecteaza se stabileste O_i în punctul de intersectie. Daca z_i-1 si z_i sunt paralele se stabileste O_i în articulatia “i”.

Se stabileste axa x_i de-a lungul perpendicularei comune la axele z_i si z_i-1 care trece prin punctul O_i, sau în directia normala la planul (z_i-1,z_i), daca z_i-1 si z_i se intersecteaza.

Se stabileste axa y_i astfel încât sa completeze sistemul cartezian de coordonate O_ix_iy_iy_i.

Se stabileste sistemul de coordonate asociat efectorului O_nx_ny_ny_n. Daca articulatia n este de rotatie se alege k_n=a de-a lungul directiei z_n-1. Se stabileste originea O_n convenabil de-a lungul lui z_n, de preferinta în centrul efectorului sau la capatul acestuia. Se alege j_n=s în directia de închidere a efectorului si se alege în=n în directia sxa. Daca forma efectorului nu este simpla se aleg x_n si y_n convenabil în asa fel încât sa se completeze sistemul de coordonate cartezian.

Parametrii Denavit-Hartenberg (parametri ce caracterizeaza complet descrierea pozitiei si a orientarii în spatiu a bratului de robot) sunt dati de urmatorul set de valori:

unghiul q_i de rotatie în jurul axei z_i-1 pentru a suprapune vectorul  x_i-1 peste vectorul x_i (paralela la x_i dusa din O_i-1).

distanta d_i masurata de-a lungul axei  z_i-1 ,de la originea o_i-1 pâna la punctul de intersectie dintre axele x_i si z_i-1.

unghiul α_i de rotatie în jurul axei x_i-1 pentru a suprapune vectorul  z_i-1 (paralela la z_i-1 dusa din O_i) peste vectorul z_i.

distanta a_i masurata de-a lungul axei x_i, de la punctul de intersectie dintre axele x_i si z_i-1 pâna la originea O_i.

Prin aceasta metoda sistemul de coordonate O_ix_iy_iz_i este obtinut din sistemul de coordonate O_i-1x_i-1y_i-1z_i-1 prin urmatoarele miscari:

o translatie cu d_i de-a lungul lui z_i-1, urmata de o rotatie cu q_i în jurul lui z_i-1;

o translatie cu a_i de-a lungul lui x_i, urmata de o rotatie cu α_i în jurul lui x_i;

Matricea care da pozitia efectorului fata de baza se obtine acumulând matricile de transformare omogena ale sistemelor de coordonate intermediare dupa cum urmeaza :

(1.1.22)

În general multimea matricilor de transformare omogena nu este comutativa. Numai în cazul în care avem o deplasare de-a lungul unei axe si o rotatie în jurul aceleasi axe, ordinea de înmultire a matricilor nu conteaza:

.

1.1.6 A doua metoda de alocare a sistemelor de coordonate conform D-H

A doua metoda de alocare a sistemelor de coordonate si de stabilire a parametrilor Denavit-Hartenberg este prezentata în figura 1.1.9:

Figura 1.1.9

Regulile folosite sunt urmatoarele:

Sistemul de coordonate cu originea O_i-1 se va plasa în articulatia 'i-1'. Primul sistem de coordonate Ox₀y₀z₀ se stabileste în baza sistemului de miscare si nu reflecta prima tendinta de miscare. Sistemul de coordonate în jurul caruia se realizeaza prima miscare, de translatie sau de rotatie, este O₁x₁y₁z_{1 .}

Axa z_i-1 este axa de miscare, adica se alege astfel încât miscarea articulatiei “i” sa fie de rotatie în jurul axei z_i-1, sau de translatie de-a lungul axei z_i-1. Cu aceasta regula se stabilesc toate axele  z_i-1 din articulatiile robotului.

Axa x_i-1 se stabileste de-a lungul perpendicularei comune între axele z_i-1 si z_{i .}

Axa y_i-1 se alege astfel încât sa completeze sistemul cartezian de coordonate O_ix_i-1y_i-1z_i-1.

Parametrii Denavit-Hartenberg sunt dati de urmatorul set de valori:

unghiul α_i de rotatie în jurul axei x_i-1 pentru a suprapune vectorul z_i-1 peste vectorul z_i (paralela la z_i dusa din O_i-1).

distanta b_i masurata de-a lungul axei x_i-1 ,de la originea O_i-1 pâna la punctul de intersectie dintre axele  x_i-1 si z_i.

unghiul q_i de rotatie în jurul axei z_i pentru a suprapune vectorul x_i-1 (paralela la x_i-1 dusa din O_i) peste vectorul x_i .

distanta d_i masurata de-a lungul axei z_i, de la originea O_i pâna la punctul de intersectie dintre axele x_i-1 si z_i.

Matricea de transformare omogena este :

(1.1.23)

Pasii algoritmului sunt urmatorii: mai întai se stabileste un sistem de coordonate de baza “0”, care este fix si ales arbitrar. Apoi se aleg axele z_i în jurul carora sau de-a lungul carora se realizaza miscarea celor n bratele ale robotului. Pentru articulatiile de rotatie, axele z_i se aleg astfel încât rotatia sa se faca în sensul pozitiv al axelor conform regulii burghiului drept, iar pentru articulatiile de translatie, axele z_i se aleg astfel încât deplasarea sa aiba loc în sensul pozitiv al axelor. Dupa ce toate axele z_i au fost stabilite, se stabilesc axele x_i astfel încât x_i (z_i,z_i+1). Daca z_i si z_i+1 se intersecteaza sau sunt paralele, alegerea lui x_i este arbitrara. Axele y_i se aleg în mod unic corespunzator regulii burghiului drept. Deoarece nu sunt folosite în determinarea parametrilor Denavit-Hartenberg pot sa nu fie figurate.

Observatie. Alegerea parametrilor Denavit-Hartenberg asa cum a fost mentionata mai sus asigura urmatoarele:

parametrii a_i si b_i sunt constanti si dependenti doar de configuratia geometrica a robotului

parametrul q_i este variabil daca articulatia “i” este o articulatie de rotatie

parametrul d_i este variabil daca articulatia “i” este o articulatie de translatie

1.2 MODELUL GEOMETRIC INVERS

În capitolul precedent a fost prezentat modelul cinematic direct, prin care se determina configuratia (pozitie si orientare) a efectorului fata de baza, functie de valorile cunoscute asociate articulatiilor. În acest capitol va fi prezentata problema mult mai dificila a modelului cinematic invers, prin care se determina setul particular al variabilelor generalizate, asociate articulatiilor, care produc o configuratie cinematica cunoscuta si dorita a efectorului.

1.2.1 Studiu de caz: robotul planar

Vom exemplifica aceasta metoda numai pentru robotul planar.

Figura 1.2.1

Daca impunem ca originea efectorului (adica punctul O_t) sa se gaseasca la coordonatele notate generic (p_x, p_y, p_z=0 în cazul robotului planar) exprimate fata de sistemul de baza si sa fie orientat cu unghiul a ca în figura 1.2.1, atunci putem scrie o prima egalitate

(1.2.1)

Cinamatica inversa aplicata acestui tip de robot presupune aflarea parametrilor q y si h pentru o matrice cunoscuta T^t₀ , adica pentru un a cunoscut si o pozitie (p_x, p_y) cunoscuta. Din egalitatea (1) rezulta o prima relatie :

cos(q y)=cos(a) adica q y a (1.2.2)

Solutia problemei cinematice inverse consta în urmatoarea procedura repetitiva: se înmulteste succesiv relatia cu inversele matricilor omogene de transformare, pentru ca succesiv variabilele generalizate sa migreze din partea stânga a valorilor necunoscute în partea dreapta a valorilor cunoscute.

În continuare se va explicita aceasta procedura pentru robotul planar :

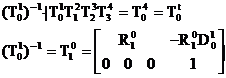
unde T⁰₁ este singura matrice dependenta de q

Scopul înmultirii este de a muta dependenta lui q din partea stânga a ecuatiei, în partea dreapta, unde se gasesc valorile cunoscute. În continuare vom considera doar ultima coloana, lucru care este notat cu un indice inferior atasat matricii, adica notatia Tⁱ_i-1j reprezinta coloana j din matricea Tⁱ_i-1.

adica .

Deci putem scrie

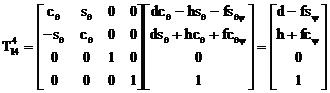
Analog putem scrie

De unde rezulta o noua relatie :

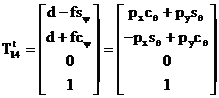(1.2.3)

În continuare premultiplicam cu 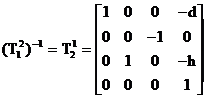si obtinem urmatoarele relatii :

, adica .

Explicit înseamna :

si

.

Egalând cei doi vectori obtinem relatia urmatoare :

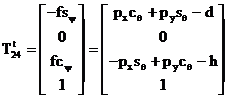(1.2.4)

Procedura se continua cu 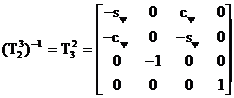si . Adica

Egalând cei doi vectori obtinem relatia

(1.2.5)

Din relatiile (1.2.1) si (1.2.2) obtinem

Din relatia (1.2.3) obtinem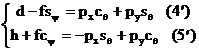

Ecuatiile obtinute din relatia (1.2.4) sunt  echivalente cu cele obtinute din relatia (1.2.1).

Din relatia (1.2.5) avem : .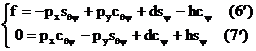

Ecuatiile si sunt de forma .

Însumând cele doua ecuatii dupa ce au fost ridicate la patrat, obtinem :

de unde deducem expresia lui h si anume :

.

Tot din sistemul anterior rezulta si valoarea unghiului q si anume :

, unde

Atan2 este o extensie a functiei trigonometrice arctangenta care tine cont de semnele numitorului si numaratorului si în acest fel furnizeaza o solutie unica.

1.2.2 Probleme propuse

1. Dându-se o pozitie dorita a efectorului, câte solutii exista pentru cinematica inversa asociata robotului planar din figura 1.2.2 ? Daca în plus si orientarea efectorului este specificata, câte solutii exista? Folositi si abordarea geometrica pentru a rezolva problema.

Figura 1.2.2

2. Aceleasi întrebari ca la problema 1, aplicate urmatorului tip de robot din figura nr 1.2.3.

3. Manipulatorul Standford are o configuratie de efector de tip sferic (figura nr 1.2.4). Dându-se o pozitie dorita d si o orientare R a efectorului

(a)  Sa se calculeze pozitia dorita pentru centrul încheieturii p_c.

(b) Sa se rezolve pozitiile cinematice inverse, adica valorile asociate primelor trei articulatii care vor plasa centrul articulatiei în punctul p_c. Exista o solutie unica? Câte solutii se pot gasi?

(c) Calculati matricea de rotatie R⁰₃. Rezolvati cinematica inversa asociata acestui manipulator gasind un set de unghiuri Euler corespunzatoare matricii de rotatie R⁰₃.

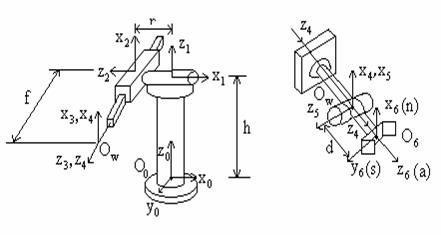
Figura 1.2.4

4. Repetati cerintele din problema 3 pentru robotul de tip Puma care de asemenea are efectorul de tip sferic. Câte solutii se pot gasi?

1.3 MODELAREA CINEMATICA A  MISCARII

1.3.1 Cazul planar

Vom nota cu X vectorul care da configuratia completa a efectorului, de dimensiune 3 (plan) si 6 (spatiu) si cu f vectorul parametrilor generalizati asociati articulatiilor bratelelor, de dimensiune n (egala cu numarul de brate

ale robotului).

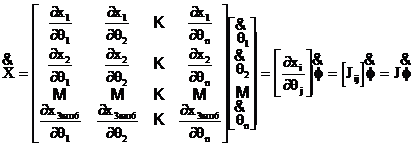              (1.3.1)

unde matricea de dimensiune 3xn sau 6xn este numita matrice Jacobian.

Daca J este matrice patratica si nesingulara J 0, , atunci putem scrie si relatia inversa :

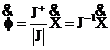(1.3.2)

Pentru robotul planar aceste ecuatii cinematice se scriu

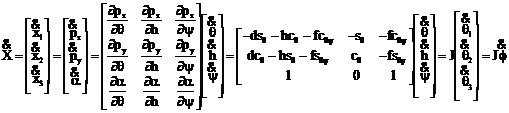(1.3.3)

Determinantul matricii Jacobian este J =-h. Relatia inversa se scrie

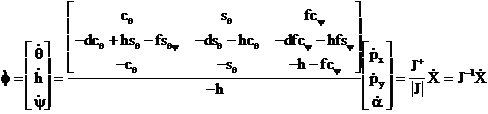(1.3.4)

În cazul robotului planar, vitezele bratelelor pot fi determinate cunoscând vitezele “carteziene”, daca h 0. Pentru ca q(t) sa fie cunoscut la orice moment trebuie scrise mai întâi ecuatiile cinematice directe.

Ce se întâmpla când J =0? Valorile variabilelor generalizate pentru care J =0 se numesc set singular de valori (generalizate) asociate bratelelor robotului. Anumite elemente ale vectorului în apropierea setului singular vor avea valori foarte mari, de exemplu în jurul acestui set va avea valori foarte mari, tinzând catre . În acest caz limita, manipulatorul se spune ca este într-o configuratie degenerata, deoarece libertatea de miscare este restrânsa.

Directiile carteziene particulare de miscare, în care miscarea este imposibila din aceasta configuratie degenerata, se numesc directii carteziene de constrângere. Cum putem afla aceste directii? Plecând de la relatia

(1.3.5)

si tinând cont de constrângerea :

(1.3.6)

obtinem : (1.3.7)

Ecuatia (1.3.7) în mod natural exprima setul de viteze carteziene , relative la sistemul de baza “0”, de-a lungul carora miscarea este posibila plecând de la aceasta configuratie degenerata.

Altfel spus, orice set pentru care reprezinta un vector de viteze de-a lungul caruia miscarea nu este posibila, sau o directie carteziana de constrângere. Deoarece pentru orice vector nenul , atunci reprezinta o astfel de directie carteziana de constrângere.

În cazul robotului planar

(1.3.8)

care înlocuit în relatia (7) ne da :

(1.3.9)

Ecuatia (1.3.9) reprezinta setul vitezelor carteziene de-a lungul carora miscarea este posibila când h=0.

Daca în plus fata de h=0 avem si conditiile q=0 si y=90 din ecuatia (1.3.9) rezulta

(1.3.10)

adica orice miscare în care efectorul are o componenta nenula în directia x (a bazei) este fizic imposibila în aceasta configuratie degenerata. În acest caz directiile carteziene de constrângere în planul sunt toate directiile de miscare cu exceptia celor paralele cu axa y. Semnificatia relatiei (10) este aratata în figura 1.3.1.

Figura 1.3.1

Daca q=30 si y=90 , în plus fata de h=0, ecuatia (1.3.9) este echivalenta cu relatia

(1.3.11)

sau .

Miscarea în planul este posibila numai daca

(1.3.12

Semnificatiile relatiilor (1.3.11) si (1.3.12) este ilustrata în figura 1.3.2.

Figura 1.3.2

Daca q=30 si y=45 (sau orice alta valoare diferita de 90 ) în plus fata de h=0 ecuatia (1.3.9) este echivalenta cu relatia :

(1.3.13)

Miscarea în planul este posibila pentru orice viteze alese arbitrar cu conditia sa se respecte relatia (13).

Lucrurile pot continua pâna la aflarea valorilor pentru acceleratii

(1.3.14)

si daca J este patrata si nesingulara, se poate scrie si relatia inversa

(1.3.15)

Figura 1.3.3

1.3.2 Cazul tridimensional

În cazul tridimensional X va avea 6 termeni, 3 pozitii si 3 orientari.

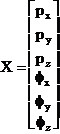(1.3.16)

Desi orientarea poate fi definita prin trei unghiuri distincte (ca yaw, pitch si roll) în general este imposibil sa se specifice orientarea prin trei rotatii independente în jurul axeler x, y, z cu unghiurile respectiv f_x f_y f_z si care sa nu depinda de ordinea în care sunt realizate. Dar variatii infinitezimale ale orientarii sunt comutative. De aceea este posibil sa se specifice variatiile în timp ale unghiurilor  f_x f_y f_z, adica vitezele unghiulare w_x w_y w_z prin trei ecuatii independente si care nu depind de ordinea miscarilor. Aceste valori nu se obtin ca în cazul planar prin derivare directa. În acest caz procedura de aflare a Jacobianului, este cea prezentata în continuare.

Se pleaca de la relatia bine cunoscuta din mecanica :

(1.3.17)

si se considera în continuare ca P este originea sistemului “q+1”. Înlocuind în (1.3.17) obtinem :

(1.3.18)

Relatia (1.3.18) se poate simplifica pentru ca 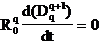, deoarece reprezinta distanta fixa dintre O_q si O_q+1 (trebuie facuta observatia importanta ca acest formalism este valabil numai pentru articulatii de rotatie, de exemplu pentru robotul PUMA). Avem deci :

(1.3.19)

Relatie (19) se va particulariza pentru diferite valori ale lui q.

(1.3.20)

deoarece este un vector fix.

(1.3.21)

Aceasta procedura poate fi repetata pentru q=3,4,t-1 si se obtine în final

(1.3.22), unde reprezinta pozitia relativa a efectorului fata de baza.

Datorita faptului ca sistemele de coordonate au fost stabilite conform conventiei Denavit-Hartenberg, este datorat rotatiei cu în jurul axei z_q. Deci putem scrie

(1.3.23)

unde k_r este un vector unitar în jurul axei z_r (pentru articulatiile de rotatie considerate). Cu aceasta observatie relatia (1.3.22) devine :

(1.3.24)

sau altfel grupate

(1.3.25)

Daca q<t, atunci este valabila urmatoarea relatie

(1.3.26)

Relatia (1.3.26) înmultita cu da :

(1.3.27)

În continuare înlocuim în relatia (1.3.25) expresia gasita în relatia (1.3.27) si obtinem :

(1.3.28)

În continuare se foloseste relatia (1.3.29) unde componentele lui k_q în sistemul “0” sunt date de a treia coloana a matricii de rotatie .

Din relatia (1.3.29) si din relatia (1.3.28) rezulta :

(1.3.30)

În continuare ne vom ocupa separat de termenul general

(1.3.31)

care este o scriere diferita a înmultirii celor doi vectori, unde reprezinta liniar a vectorului .

Daca scriem doar versorii asociati vectorilor, relatie (1.3.31) devine

(1.3.32)

În relatia (1.3.28) înlocuim acum ultima relatie obtinuta (1.3.32) si obtinem

(1.3.33)

Relatia (1.3.33) este relatia care permite aflarea primelor trei rânduri din matricea Jacobianului J.

În continuare stiim ca vectorul 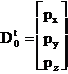deci

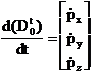(1.3.34)

Vectorul acceleratiilor unghiulare :

(1.3.35)

Relatia finala de calcul a Jacobianului pentru cazul robotilor cu articulatii de rotatie, care se deplaseaza într-un spatiu tridimensional este data de îmbinarea ecuatiilor (1.3.33), (1.3.34) si (1.3.35)

(1.3.36)

unde :

(1.3.37)

Matricea Jacobian este data de relatia (1.3.37). Ultima coloana apare doar în cazul în care s-a asociat un reper “t” efectorului si acesta este fix, adica nu exista o rotatie fata de sistemul anterior. Primele trei rânduri ale lui J se fi numesc Jacobianul de pozitie si se noteaza cu J_P, iar celelalte trei se numesc Jacobianul de orientare. Trebuie facuta o ultima observatie si anume accea ca J_P se poate obtine si direct prin derivare ecuatiilor care exprima pozitia efectorului functie de variabilele bratelelor, ecuatii obtinute în urma modelului geometric direct.

1.3.3 Câteva consecinte ale manipulatoarelor cu efector sferic

Tehnica de aflare a miscarii cinematice poate fi simplificata pentru o clasa aparte de roboti, care au 6 grade de libertate si efectorul de tip sferic (cum este cazul robotului PUMA).

Pentru orice robot cu 6 bratele si efectorul de tip sferic ecuatiile de configurare cinematica pot fi separate în partea de pozitionare si partea de orientare. Cele trei unghiuri finale ale bratelelor pot fi calculate separat în functie de o solutii de pozitionare si de orientare dorite penntru punctul O_w (care este punctul de intersectie a axelor de rotatie ale efectorului).

Vom calcula vitezele de translatie ale efectorului (O_w) în functie de primele trei unghiuri ale robotului.

Figura 1.3.4

Figura 1.3.4 se refera la robotul PUMA, dar este general valabila pentru orice manipulator sferic. Conform figurii nr 4 avem

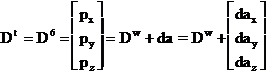(1.3.38)

Derivând relatia (1.3.38) obtinem

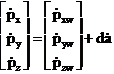(1.3.39)

cu vectorul componentelor vitezei de translatie a, d fiind distanta fixa de la O_w la O_t.

Ecuatiile cinematice se scriu acum

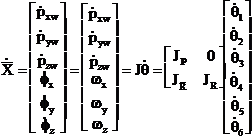(1.3.40)

adica 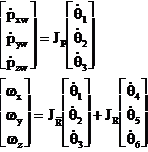 (1.3.41)

Pentru aceasta clasa particulara de manipulator primele trei bratele sunt de rotatie, deci putem scrie

Din relatia (1.3.40) rezulta ca (1.3.42)

Daca bratul q este prismatic (de translatie) în relatia (1.3.42) putem pune .

Tot din relatia (1.3.40) rezulta ca (1.3.43)

care va fi o functie de cele 6 deplasari. Deoarece 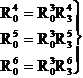relatia (1.3.43) se scrie :

(1.3.44) , unde (1.3.45)

Deci Jacobianul se poate calcula conform formulei , unde valorile particulare ale componentelor sale sunt date de relatiile (1.3.41), (1.3.42), (1.3.44) si (1.3.45)

Determinantul lui J poate fi scris sub forma :

.

Singularitatile Jacobianului, setul valorile singulare ale variabilelor generalizate sunt date de :

(1.3.46)

si pot fi separate în doua seturi distincte.

Setul de valorilor generalizate singulare pentru “pozitie”

(1.3.47)

si setul de valorilor generalizate singulare pentru orientare

(1.3.48)

Deoarece J_P depinde doar de primele trei valori generalizate, setul valorilor singulare de pozitionare va depinde doar de q₁ q₂ q₃, iar setul valorilor singulare de orientare va depinde doar de  q₄ q₅ q₆

În concluzie, conditia suplimentara de manipulator sferic, ne permite sa separam complet singularitatile de pozitionare si de orientare, care pot fi determinate si evaluate independent.

Inversa matricii Jacobian este

(1.3.49)

unde daca avem simultan conditiile .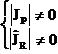

În acest caz determinarea valorilor generalizate în functie de valorile carteziene se poate face de asemenea separat.

Pentru pozitionare avem :

(1.3.50)

si pentru orientare

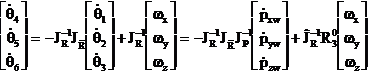(1.3.51)

Relatiile cinematice directe pentru acceleratiile de “pozitionare” sunt

(1.3.52)

Relatiile cinematice inverse pentru acceleratiile de “pozitionare” sunt

(1.3.53)

Relatiile cinematice directe pentru acceleratiile de “orientare” sunt

(1.3.54)

Relatiile cinematice directe pentru acceleratiile de “orientare” sunt

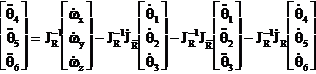(1.3.55)

1.3.4 Studiu de caz: robotul PUMA

Vom începe prin calculul Jacobianului de pozitionare J_P,, care se poate gasi prin derivarea ecuatiilor obtinute în urma modelului geometric direct.

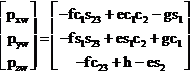(1.3.56)

Diferentierea directa a relatiei (1.3.56) conduce la urmatoarea relatie

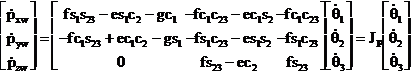(1.3.57)

Se calculeaza determinantul lui J_P pentru a gasi pozitiile degenerate, asociate cu interiorul spatiului de lucru. Calculam mai întai ca (1.3.58) astfel încât setul singular al pozitiilor este determinat de doua situatii:

sau deoarece q₃ nu poate atinge (1.3.59)

si

(1.3.60)

Primul caz (relatia (1.3.59)) corespunde unei pozitii degenerate când bratele sunt complet extinse. Cel de-al doilea caz (relatia (1.3.60)) corespunde situatiei ilustrate în figura nr 5, unde s-a realizat proiectia bratelelor 2 si 3 pe planul în cazul în care avem egalitatea. În figura 1.3.5 termenul si termenul reprezinta proiectia punctului O₃ pe axa x₁.

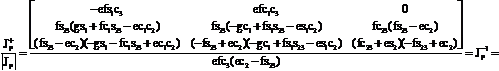
(1.3.61)

Figura 1.3.5

În continuare vom face calculele pentru partea de orientare.

Prima observatie este ca pentru robotul PUMA 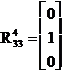si deci

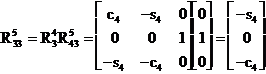si .

Folosind acesti vectori obtinem

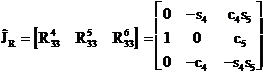(1.3.62)

cu . De aici se poate trage concluzia ca singura orientare degenerata, care corespunde unei singularitati a Jacobianului, este data de setul singular de valori singulare pentru orientare, adica de relatia sinq₅=0 sau q₅=0 , deoarece q₅ nu poate atinge 180 . Aceasta conditie corespunde cazului când z₄ si z₆ se aliniaza. De asemenea când efectorul este într-o asemenea orientare degenerata, ambele unghiuri q₄ si q₆ produc aceeasi miscare de rotatie, astfel un grad de libertate pentru rotatie s-a pierdut.

În continuare observam ca

(1.3.63)

si de asemenea

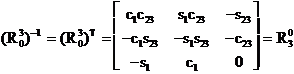(1.3.64)

Pâna acum am calculat relatia (1.3.61) si folosind relatiile (1.3.63) si (1.3.64) obtinem

(1.3.65)

astfel încât singurul termen care mai trebuie calculat este :

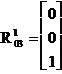, , si deci

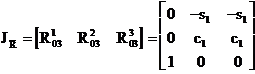(1.3.66)

Determinarea lui J si respectiv J^-1 pentru robotul PUMA este acum completa, folosind relatiile (1.3.61), (1.3.65) si (1.3.66).

Pentru a determina directiile carteziene de constrângere avem si , de unde avem , adica .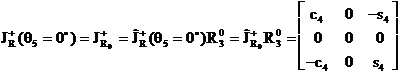

Conditiile de constrângere a miscarii care sunt date de 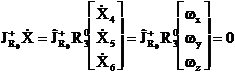, ne conduce la urmatoarea relatie (1.3.67)

De aceea când si realtia (1.3.67) conduce la

c₂₃=s₁=s₄=0 adica (1.3.68) .Relatia (1.3.68) înseamna ca miscarea unghiulara a originii efectorului (adica a sistemului 6 de coordonate) în jurul axei de baza z, adica axei z₀ este imposibila.

1.3.5 Probleme propuse

1. Consideram robotul planar având trei articulatii de rotatie (figura 1.3.6) si lungimea bratelelor respectiv d, h, si bratul trei de lungime 0 (a efectorului).

(a) Determinati grafic ecuatiile cinematice directe asociate cu acest manipulator, adica valorile p_x, p_y si a ca functii de q₁ q₂ q₃

(b) Diferentiati cele trei ecuatii obtinute la punctul (a) în scopul obtinerii Jacobianului J (3x3).

(c) Determinati J si J^-1.

(d) Identificati toate configuratiile degenerate asociate cu acest tip de manipulator.

Figura 1.3.6

2. Determinati explicit matricea (3x3) Jacobian de orientare pentru robotul Microbot, notata cu si identificati setul singular al valorilor generalizate, adica valorile lui q₁ q₂ q₃ pentru care =0. Discutati semnificatia rezultatelor obtinute vis a vis de abilitatea de a obtine orientari dorite, arbitrare ale efectorului.

3. Determinati explicit directiile de constrângere carteziene asociate robotului Puma când q₃=-90 si q₁ q₂=0 . Schitati o vedere de sus a robotului în aceasta pozitie degenerata si verificati grafic rezultatele obtinute.

4. Scrieti expresia întregului Jacobian (6x6) asociat tipului de robot Standford.