| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
OPTIMIZAREA PORTOFOLIILOR CU N ACTIUNI
1. Prezentarea problemei
Similar celor prezentate in capitolul 4, consideram disponibil istoricul randamentelor procentuale pe m perioade de timp pentru fiecare actiune dintr-un grup de n actiuni. Notatiile utilizate in continuare sunt cele prezentate in capitolul 4.
Functiile randament, respectiv risc, sunt reprezentate matriceal prin,
(1)
![]()
(2)
![]() ,
,
unde
![]()
![]()
![]() ,
, ![]()
De
asemenea, in reprezentare matriceala, relatia ![]() devine,
devine,
![]()
unde ![]() este vectorul unitar n-dimensional.
este vectorul unitar n-dimensional.
Prin
utilizarea relatiei (3), variabila ![]() este eliminata
este eliminata ![]() si functiile randament si risc
sunt exprimate in termenii
si functiile randament si risc
sunt exprimate in termenii ![]() . Fie
. Fie ![]() , vector de dimensiune n-1,
, vector de dimensiune n-1, ![]() vector n-dimensional si B matrice de dimensiune
vector n-dimensional si B matrice de dimensiune ![]() , cu primele n-1 linii liniile corespunzatoare matricei
unitate
, cu primele n-1 linii liniile corespunzatoare matricei
unitate ![]() si ultima linie formata cu elementul -1,
si ultima linie formata cu elementul -1,
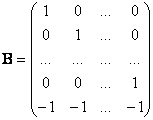
Cu aceste notatii, obtinem,
(4)
![]() .
.
2. Definirea problemelor de oprimizarea portofoliilor cu n actiuni in termenii problemelor de optimizare fara constrangeri
Similar
celor prezentate in capitolul 4, procedura MINRISC0 defineste problema
primara de minimizare a riscului in cazul unui portofoliu definit de
fractiunile de investitii ![]() . Prin utilizarea relatiei (4), rezulta,
(Bartholomeu-Biggs, 2005)
. Prin utilizarea relatiei (4), rezulta,
(Bartholomeu-Biggs, 2005)
MINRISC0:
(5)
Minimizeaza ![]()
Relatia
(5) defineste o problema de optimizare fara constrangeri,
in n-1 variabile. Daca ![]() este o solutie a problemei (5), atunci portofoliul de
risc minim, notat
este o solutie a problemei (5), atunci portofoliul de
risc minim, notat ![]() , este definit prin,
, este definit prin,
(6)![]() si
si ![]() .
.
O
serie de metode care rezolva problema minimizarii unei functii
de mai multe variabile utilizeaza vectorul derivatelor partiale de
ordinul I, numit gradient. Daca V este functie de m variabile, atunci gradientul lui V, notat ![]() sau
sau ![]() , este definit prin,
, este definit prin,
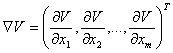 .
.
Gradientul functiei obiectiv din relatia (5) este,
(7)
![]()
Pentru
rezolvarea problemelor de optim, unele metode necesita si calculul
derivatelor partiale de ordinul II, adica a matricei Hessian.
Daca V este functie de m variabile, atunci matricea Hessian,
notata ![]() sau
sau ![]() , este definita prin,
, este definita prin,

Hessianul functiei obiectiv din relatia (5) este,
(8)![]()
Problema RISCMIN1M, definita in capitolul 4, poate fi exprimata in termenii unei probleme de optimizare fara restrictii prin utilizarea relatiei (4), astfel, (Bartholomeu-Biggs, 2005)
(9)
Minimizeaza ![]()
Pentru calculul vectorului gradient si al matricei Hessian pentru functia F definita in (9), consideram reprezentarea,
![]() ,
,
unde
![]()
![]() si
si
![]()
Sunt obtinute relatiile,
![]()
unde
![]() si
si
![]() .
.
Similar, este obtinuta matriea Hessian, prin,
![]()
unde
![]() si
si
![]() este o matrice cu
rangul 1, pentru orice i,j,
este o matrice cu
rangul 1, pentru orice i,j, ![]() ,
,
![]()
Problema RANDAMENTMAX1 este reformulata in termenii RANDAMENTMAX1M (vezi capitolul 4) si, prin utilizarea relatiei (4) rezulta problema de optimizare fara restrictii, (Bartholomeu-Biggs, 2005)
Minimizeaza ![]()
Expresiile care definesc gradientul si Hessianul functiei definite in (7.10) sunt obtinute prin reprezentarea,
![]() ,
,
unde
![]()
![]() si
si
![]() .
.
Rezulta,
![]()
![]()
unde
![]() este matrice de rangul
I; pentru orice i,j,
este matrice de rangul
I; pentru orice i,j, ![]() ,
,
![]() .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1027
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved