ALGORITMII

ALGORITMII

Conceptul de algoritm

Algoritmul este abstract si trebuie diferentiat de reprezentarea sa. In acest context, al distinctiei dintre algoritm si reprezentarea sa, se poate lamuri si diferenta dintre doua concepte inrudite - program si proces.

Programul este reprezentarea unui algoritm (reprezentarea formala a unui algoritm proiectat in vederea unei aplicatii informatice).

Procesul este definit ca fiind activitatea de executie a programului, dar putem defini procesul ca activitatea de executie a unui algoritm. Deci, programele, procesele si algoritmii sunt entitati inrudite, dar distincte.

Un algoritm consta dintr-o multime ordonata de pasi executabili, descrisi fara echivoc, care definesc un proces finit.

Fig. 2.2.1. Definitia algoritmului

Analizand definitia algoritmului, ne vom opri asupra cerintei ca pasii care descriu algoritmul sa fie ordonati, deci trebuie sa aibe o ordine clara in executia pasilor.

Exista si algoritmi paraleli care contin mai multe secvente de pasi, fiecare secventa urmand sa fie executata de alt procesor in cadrul unei masini multiprocesor (deci nu este vorba numai de un fir de executie).

In continuare vom analiza cerinta ca algoritmul sa fie compus din pasi executabili. Fie instructiunile:

Pasul 1: Construiti o lista cu toate numelele intregii pozitive.

Pasul 2: Sortati lista in ordine descrescatoare.

Pasul 3: Extrageti primul numar intreg din lista rezultata.

Aceste instructiuni nu descriu un algoritm, deoarece pasul 1 si 2 sunt imposibil de executat (nu se poate construi o lista cu toti intregii pozitivi si intregii pozitivi nu pot fi asezati in ordine descrescatoare.

Alta cerinta, descrierea fara echivoc a pasilor algoritmului inseamna ca, in timpul executiei programului, informatiile din fiecare stare a procesului trebuie sa fie suficiente pentru a determina unic si complet actiunile in fiecare pas.

Executia algoritmului nu necesita creativitate, ci doar capacitatea de a urma instructiunile. Descrierea algoritmului ca un proces finit inseamna ca executia algoritmului trebuie sa aibe sfarsit.

Trebuie realizata o delimitatare intre procesele care se termina cu un raspuns- rezultat si cele care se executa la infinit, fara a ajunge la vreun rezultat.

Termenul de algoritm este folosit adesea intr-o acceptiune mai putin riguroasa pentru a descrie procese care nu sunt neaparat finite. (Ex. Algoritmul de impartire fara rest a numerelor intregi, impartirea lui 1 la 3).

Reprezentarea algoritmilor

P r i m i t i v e

Reprezentarea unui algoritm nu se poate face in absenta unui limbaj. In cazul oamenilor acest limbaj poate fi limbajul natural uzual sau limbajul imaginilor. Aceste canale naturale de comunicare duc la neintelegeri, termenii folositi pot avea mai multe sensuri.

Informatica abordeaza aceste probleme stabilind o multime bine definita de blocuri elementare care stau la baza reprezentarii algoritmilor. Aceste blocuri elementare poarta numele de primitive.

Definirea precisa a primitivelor elimina ambiguitatea si permite un grad uniform de detaliere.

O multime de reguli care guverneaza modul in care aceste primitive pot fi combinate pentru reprezentarea ideilor mai complexe constituie un limbaj de programare.

Fiecare primitiva consta din doua elemente: sintaxa si semantica. Sintaxa se refera la reprezentarea simbolica a primitivei, in timp ce semantica se refera la conceptul reprezentat (semnificatia primitivei respective).

Pentru a reprezenta algoritmi destinati calculatorului utilizand un ansamblu de primitive, se poate porni de la instructiunile pe care calculatorul stie sa le execute. Detalierea algoritmilor la acest nivel este incomoda, in mod normal se utilizeaza primitive de nivel mai inalt, construite pe baza primitivelor de nivel scazut oferite de limbajul-masina. Rezulta astfel un limbaj de programare formal, in care algoritmi pot fi exprimati intr-o forma conceptual mai inalta decat in limbajul-masina.

P s e u d o c o d u l

Vom prezenta in continuare un sistem de notare mai intuitiv, cunoscut sub numele de pseudocod. O metoda de obtinere a pseudocodului este de a relaxa pur si simplu regulile limbajului formal in care va fi exprimata varianta finala a algoritmului.

Ceea ce ne propunem este sa discutam despre dezvoltarea si prezentarea algoritmilor fara sa ne oprim asupra unui limbaj de programare. Ne propunem sa reprezentam anumite structuri care pot deveni primitive. Printre structurile mai des intalnite remarcam:

Selectarea intre doua activitati in functie de indeplinirea unei conditii.

Fiecare dintre aceste instructiuni poate fi rescrisa astfel incat sa respecte structura:

if (conditie) then (activitate)

else (activitate)

unde am folosit cuvintele-cheie if (daca), then (atunci) elese (astfel) pentru a introduce substructurile din cadrul structurii principale si paranteze pentru delimitarea granitelor dintre aceste substructuri.

Adoptand pentru pseudocod aceasta structura sintactica, am obtinut o metoda uniforma de exprimare a unei structuri semantice des intalnite.

In cazurile in care activitatea alternativa (else) lipseste, vom utiliza sintaxa mai scurta:

if (conditie) then (activitate).

2) O alta structura algoritmica [intalnita] este executarea repetata a unei instructiuni sau a unei secvente de instructiuni atata timp cat o anumita conditie este adevarata. Modelul pseudocodului este:

while (conditie) do (activitate).

O astfel de instructiune inseamna verificarea conditiei, executarea activitatii si revenirea la verificarea conditiei. Cand conditia nu mai este indeplinita, se trece la executarea instructiunii care urmeaza.

Uneori ne referim la anumite valori prin intermediul unor nume sugestive.

Pentru astfel de asocieri se utilizeaza:

assign (nume) the value (expresie)

unde nume este un nume descriptiv, iar expresie indica valoarea care este asociata numelui respectiv.

Lizibilitatea programului poate fi imbunatatita prin identare (adica scriere pozitionata pe conditii logice).

Exemplu

if (articolul este impozabil)

then [if (pret > limita)

then (plateste x)

else (plateste y)]

else (plateste z).

Vom folosi pseudocodul pentru a descrie activitati care sa fie utilizate ca instrumente abstracte in alte aplicatii, aceste unitati de program le vom numi in continuare procedura si vom folosi cuvantul procedure pentru atribuirea fiecarui modul de pseudocod un nume.

procedure nume.

Aceasta instructiune introductiva va fi urmata de instructiunile care descriu actiunea modulului respectiv. In figura 2.2.2 este prezentat pseudocodul unei proceduri numita Salutari, care tipareste de trei ori mesajul "Hello":

procedure Salutari

assign Count the value 3

while Counct 0 do

(tipareste mesajul "Hello" si

assign Count the value Count 1).

Fig. 2.2.2. Procedura Salutari exprimata in pseudocod

Atunci cand este nevoie de efectuarea procedurii altundeva in cadrul secventei pseudocodului, procedura va fi apelata prin nume.

Procedurile trebuie sa fie cat mai generale posibil. Astfel o procedura care sorteaza orice lista de nume, trebuie sa fie scrisa in asa fel incat lista respectiva sa nu fie specifica procedurii, ci sa fie desemnata in reprezentarea acesteia sub un nume generic. Vom adopta conventia de a scrie aceste nume generice intre paranteze pe acelasi rand cu numele procedurii.

(Ex.) procedure Sort (List).

Atunci cand avem nevoie de serviciile procedurii Sort, va fi identificata lista are se substituie listei List. (Ex.):

¾ se aplica procedura Sort asupra listei cu membrii organizatiei;

¾ se aplica procedura Sort asupra listei cu elevii clasei.

Nu trebuie pierdut din vedere faptul ca scopul in care folosim pseudocodul este sa creionam algoritmi, nu sa scriem un program.

3.- Dezvoltarea algoritmilor

Dezvoltarea unui program consta din doua activitati:

¾ dezvoltarea algoritmului;

¾ reprezentarea algoritmului ca program.

Pana acum ne-a preocupat problema reprezentarii algoritmilor, dar stabilirea algoritmului constituie, in general, cea mai incitanta etapa a dezvoltarii software-ului.

Teoria rezolvarii problemelor

Capacitatea de a rezolva diferite probleme ramane mai degraba un talent artistic care trebuie dezvoltat.

Etapele pentru rezolvarea problemelor, definite in linii mari de matematicianul Polya (1945), raman valabile si astazi ca principii de baza:

Faza 1. Intelegerea problemei.

Faza 2. Conceperea unui plan de rezolvare a problemei.

Faza 3. Punerea in practica a planului respectiv.

Faza 4. Evaluarea solutiei din punctul de vedere al corectitudinii si

ca potential instrument pentru rezolvarea altor probleme.

In contextul dezvoltarii programelor, aceste etape devin:

Faza 1. Intelegerea problemei.

Faza 2. Conceperea unei metode de rezolvarea problemei prin

procedura algoritmica.

Faza 3. Formularea algoritmului si reprezentarea lui ca program.

Faza 4. Evaluarea programului din punctul de vedere al corectitudinii

si ca potential instrument pentru rezolvarea altor probleme.

Importanta primului pas

Vom identifica pe scurt cateva metode de rezolvare a problemelor. Toate aceste metode au ceva in comun si anume: important este primul pas.

Acest prim pas se poate realiza prin mai multe metode:

1) Una dintre aceste metode ar fi sa procedam invers, anume: daca se doreste a se gasi o metoda de a obtine o anumita iesire pe baza unei intrari date, se porneste de la valoarea de iesire, incercand sa se ajunga la valoarea de intrare.

2) O alta metoda este aceea de a se cauta o problema inrudita cu cea care trebuie rezolvata mai simplu sau care are deja o solutie. Se va incerca aplicarea solutiei problemei inrudite si asupra problemei initiale. Aceasta metoda este foarte utila in contextul dezvoltarii programelor pentru care dificultatea consta in gasirea algoritmului general care sa permita rezolvarea tuturor cazurilor.

3) Alta metoda este aceea a rafinarii pas cu pas. Aceasta tehnica porneste de la impartirea problemei in mai multe subprobleme. Metoda permite abordarea problemei generale in mai multe etape, in ideea ca fiecare in parte este mai usor de rezolvat decat problema in ansamblul ei. In continuare subproblemele vor fi la randul lor descompuse in mai multe etape, pana cand se ajunge la o serie de subprobleme usor de rezolvat.

Rafinarea pas cu pas este o metodologie descendenta (top-down), care merge de la general catre particular. Exista, de asemenea, si metodologia ascendenta (bottom-up) care porneste de la cazurile particulare catre cazul general.

Solutiile obtinute prin metoda rafinarii pas cu pas au in mod natural o structura modulara, motiv pentru care aceasta metoda este apreciata.

Un algoritm cu o structura modulara poate fi usor adoptat la o reprezentare modulara, ceea ce simplifica mult gestionarea activitatii de dezvoltare a programului propriu-zis. De asemenea, modulele rezultate din aplicarea metodei de rafinare pas cu pas sunt pe deplin compatibile cu ideea de lucru in echipa, modul cel mai raspandit de dezvoltare a unui produs software.

Dezvoltarea multor proiecte software pentru prelucrarea datelor presupune o dezvoltare a unei componente organizatorice. Problema nu presupune descoperirea unui algoritm uluitor, ci organizarea coerenta a sarcinilor care trebuie duse la indeplinire.

In concluzie, dezvoltarea algoritmilor ramane mai degraba un talent care se dezvolta in timp, decat o stiinta foarte exacta cu metodologii bine stabilite.

4.- Structuri iterative

In cadrul structurilor iterative unele instructiuni se repeta ciclic. Vom prezenta in continuare cativa algoritmi "celebri": cautarea secventiala si binara.

Algoritmul de cautare secventiala

Scopul acestui algoritm este determinarea unei valori daca exista sau nu in cadrul unei liste.

Presupunem ca lista a fost sortata pe baza unei reguli oarecare, functie de entitatile componente (o lista de nume respecta ordinea alfabetica, o lista de numere respecta ordinea crescatoare/descrescatoare). Pentru exemplificare, propunem urmatorul algoritm: cautam intr-o lista atata timp cat mai sunt nume si numele-tinta este mai mic decat numele curent.

In pseudocod, acest proces se reprezinta astfel:

se selecteaza primul articol din lista ca articol de test

while (valoare-tinta > articol-test si mai sunt articole de

luat in considerare)

do ( selecteaza urmatorul articol din lista ca

articol de test).

La iesirea din aceasta structura, articolul de test va fi mai mare sau egal cu numele-tinta, fie va fi ultimul nume din lista.

In oricare din aceste cazuri putem determina daca procesul s-a incheiat cu succes prin compararea valorii articolului de test cu valoarea-tinta. Pentru aceasta se adauga la valoarea rutinei in pseudocod (deja scrisa) urmatoarea instructiune:

if (valoare-tinta = valoare articol-test)

then (declara cautarea un succes)

else (declara cautarea un esec).

Am facut ipoteza (presupunerea) ca lista contine cel putin un articol. Totusi vom plasa rutina pe ramura else a instructiunii:

if (lista este goala)

then (declara cautarea un esec)

else ().

In acest mod vom obtine procedura din fig. 2.2.3.

procedure Search (list target value)

if (lista este goala)

then (declara cautarea un esec)

else [(selecteaza primul articol din list ca articol de test)

while(target value = articolul de test si mai sunt articole

de luat in considerare)

do (selecteaza urmatorul articol din list ca articol de

test)

if (target value = articolul de test)

then (declara selectarea un succes)

else (declara cautarea un esec)]

Fig. 2.2.3. Algoritm de cautare secventiala reprezentat in pseudocod

(sequential search algoritm).

Acest algoritm este folosit pentru listele de mici dimensiuni sau cand utilizarea lui este dictata de alte considerente.

Controlul ciclurilor

Utilizarea repetata a unei instructiuni sau a unei secvente de instructiuni este unul din conceptele algoritmice cele mai importante.

O metoda de implementare a acestui concept este structura iterativa denumita ciclu/bucla (loop).

In cadrul buclei o serie de instructiuni, numita corpul buclei, este executat in mod repetat sub supravegherea unui proces de control.

Ex. while (conditie) do (corpul ciclului).

Instructiunea while de mai sus reprezinta o structura ciclica deoarece executia ei conduce la parcurgerea ciclica a secventei: testeaza conditia; executa corpul ciclului; testeaza conditia; executa corpul ciclului, , testeaza conditia, pana cand conditia este indeplinita. Sa analizam mai indeaproape si instructiunea de control.

Controlul unui ciclu (bucle) consta in trei activitati: initializare, testare, modificare, asa cum se prezinta si in fig. 2.2.4.:

initializare = stabileste o stare initiala care poate fi modificata in vederea

atingerii conditiei de incheiere

testare = compara conditia curenta cu conditia de incheiere si, in caz de

egalitate, incheie procesul de repetare

modificare = schimba starea astfel incat aceasta sa avanseze catre conditia de

incheiere

Fig. 2.2.4. Componentele controlului repetitiv

Exista doua structuri de tip bucla foarte raspandite si anume:

while (conditie) do (activitate) care se reprezinta prin schema logica (flowchart) din fig. 2.2.5.

Conditie Fals

de

test

Adevarat

Fig. 2.2.5. Structura ciclului de tip while

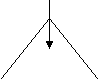
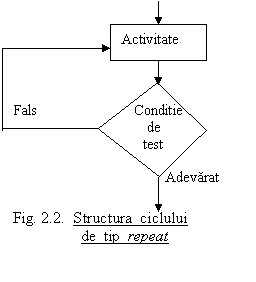
In cazul structurii while testarea conditiei de incheiere se face inaintea executarii corpului ciclului. A doua structura tip bucla, reprezentata in fig. 2.2., solicita sa se execute mai intai corpul ciclului si dupa aceea sa se testeze conditia de incheiere. Pentru reprezentarea schemei din fig. 2.2. in pseudocod se utilizeaza urmatoarea formulare :

repeat (activitate) until (conditie).

Ca exemplu suplimentar de utilizare a structurilor iteractive vom prezenta algoritmul de sortare prin inserare.

Algoritmul de sortare prin inserare sorteaza o lista extragand in mod repetat cate un articol si inserandu-l in pozitia corespunzatoare ordinii dorite.

procedure Sort (lista)

if (lista contine doua sau mai multe articole) then

[(umbreste portiunea din lista de la al doilea pana la ultimul articol;

repeat (elimina umbra din primul articol al portiunii umbrite din

lista si identifica acest articol drept pivot; muta pivotul

intr-o locatie temporara lasand in lista un spatiu gol);

while (exista un nume deasupra spatiului si acest nume este mai

mare decat pivotul)

do (muta numele de deasupra spatiului in spatiul gol,

lasand un spatiu deasupra numelui respectiv;

muta pivotul in spatiul gol din lista)

until (orice umbra din lista a fost eliminata).

Fig. 2.2.7. Sortarea prin inserare

5. Structuri recursive

Structurile recursive reprezinta o alternativa de realizare a proceselor repetitive fara a utiliza cicluri. Pentru a intelege aceasta tehnica vom discuta algoritmul de cautare binara (binary search).

Algoritmul de cautare binara

Vom relua problema cautarii unui articol intr-o lista sortata abordand metoda pe care o folosim cand cautam un cuvant in dictionar.

La cautarea intr-un dictionar incepem prin a deschide dictionarul la o pagina din zona in care credem ca se afla articolul cautat.

S-ar putea sa gasim cuvantul chiar in pagina respectiva, daca nu, trebuie sa continuam cautarea. Numai ca am restrans (deja) zona de cautare, putandu-ne rezuma fie la zona dinaintea pozitiei curente, fie la cea de dupa pozitia curenta.

Fig. 2.2.8 este reprezentarea nucleului cautarii binare in pseudocod a acestui mod de cautare aplicat asupra unei liste generice.  

In aceasta situatie nu avem avantajul de a sti cu aproximatie in ce zona se afla articolul cautat, asa ca instructiunile din figura ne spun sa incepem prin a deschide lista la articolul din "mijloc".

In cazul cand lista are un numar par de elemente, prin articol de mijloc vom intelege primul articol din cea de a doua jumatate a listei.

Daca articolul astfel selectat nu este cel cautat, rutina ofera doua alternative, ambele oferind o cautare efectuata cu ajutorul unei proceduri numita search.

Selecteaza "mijlocul" listei list ca articol de test; executa unul dintre urmatoarele blocuri de instructiuni, in functie de situarea valorii-tinta Target/Value fata de articolul de test.

Target Value = articol de test (declara cautarea incheiata cu succes)

Target Value < articolul de test [(aplica procedura search pentru a vedea daca Target Value este in portiunea din list de deasupra articolului de test) si

if (acea cautare este incununata de succes)

then (declara aceasta cautare incununata de succes)

else (declara aceasta cautare incheiata cu esec)]

Target Value > articolul de test [aplica procedura search pentru a vedea daca Target Value este in portiunea din list de sub articolul de test si

if (acea cautare este incununata de succes)

then (declara aceasta cautare incheiata cu succes)

else (declara aceasta cautare incheiata cu esec)].

Fig. 2.2.8. Nucleul cautarii binare

Se observa ca procedura permite si rezolvarea cazului cautarii intr-o lista goala daca va fi completata, obtinandu-se pentru cautarea binara programul in pseudocod prezentat in fig. 2.2.9.

procedure search (lista, Target Value

if (lista este goala)

then (declara cautarea incheiata cu esec)

else [selecteaza "mijlocul" listei cu articol de test; executa una dintre urmatoarele

blocuri de instructiuni, in functie de situarea valorii-tinta Target Value fata de

articolul de test

Target Value = articolul de test;

(declara cautarea incheiata cu succes)

Target Value < articolul de test

(aplica procedura search pentru a vedea daca Target Value este in portiunea din lista de deasupra articolului de test, si

if (acea cautare este incununata de succes)

then (declara aceasta cautare incheiata cu succes)

else (declara aceasta cautare incheiata cu esec)]

Target Value > articolul de test

[aplica procedura search pentru a vedea daca Target Value este in portiunea din lista de sub articolul de test si

if (acea cautare este incununata de succes)

then (declara aceasta cautare incheiata cu succes)

else (declara aceasta cautare incheiata cu esec)].

Fig. 2.2.9. Algoritmul cautarii binare reprezentata in pseudocod

- Eficienta si corectitudine

Doua dintre subiectele legate de algoritmi sunt importante si vor fi abordate in continuare: eficienta si corectitudinea acestora.

Eficienta algoritmilor

Desi calculatoarele actuale executa milioane de instructiuni pe secunda, eficienta proiectarii algoritmilor ramane o preocupare importanta, deoarece adesea diferenta dintre un algoritm eficient si unul ineficient constituie diferenta intre o solutie practica si una inaplicabila.

Sa analizam o problema practica pentru a intelege mai bine eficienta algoritmilor.

Problema consta in regasirea inregistrarii unui student din multimea inregistrarilor studentilor (cca 30.000 studenti) din cadrul unei universitati.

Pentru inceput vom analiza modul de regasire folosind algoritmul de regasire secventiala.

Acest algoritm parcurge lista de la inceput, comparand fiecare articol cu numarul cautat. Necunoscand valoarea-tinta, nu putem spune cat de departe va merge in lista aceasta cautare. Statistic ne asteptam ca media sa fie pe la jumatatea listei. Prin urmare, in medie algoritmul secvential va investiga cca 15.000 de inregistrari pentru fiecare cautare. Daca regasirea si verificarea unei inregistrari dureaza o milisecunda, o astfel de cautare dureaza cca 15 secunde. O zi de lucru are 28.800 secunde; daca s-ar lucra continuu, algoritmul de cautare secventiala va permite sa se efectueze cca 1.9002.000 de cautari pe zi. Deci regasirea celor 30.000 de studenti va dura cca. 15 zile.

Acum a venit randul sa analizam cautarea binara. Aceasta cautare incepe prin a compara valoarea-tinta cu articolul situat in mijlocul listei. Este posibil sa nu gaseasca articolul cautat, dar se reduce aria cautarii la jumatate din lista initiala. Deci dupa prima interogare, cautarea binara mai are de luat in calcul cel mult 15.000 de inregistrari. Dupa a doua interogare raman cel mult 7.500 si asa mai departe, pana la cea de a 15-a interogare cand se gaseste articolul cautat. Daca o interogare dureaza o milisecunda, atunci regasirea unei anumite inregistrari se va face in maximum 0,015 secunde. Aceasta inseamna ca pentru a gasi inregistrarile corespunzatoare ale celor 30.000 de studenti, este nevoie de cel mult 7,5 minute.

Cele doua rezultate arata clar o imbunatatire substantiala a timpului de cautare folosind algoritmul de cautare binara.

Verificarea produselor software

Verificarea software-ului este o sarcina dintre cele mai impor-tante, iar cautarea unor tehnici eficiente de verificare constituie unul dintre cele mai active domenii de cercetare.

Una din directiile de cercetare este incercarea de a demonstra corectitudinea programelor prin aplicarea tehnicilor logicii formale. Deci, ideea de baza este reducerea verificarii la o procedura de logica formala care sa nu fie afectata de concluziile care pot rezulta din aplicarea unor argumente intuitive.

Pentru demonstrarea corectitudinii unui program vom porni de la presupunerea ca la inceputul executiei acestuia sunt indeplinite un numar de conditii, numite preconditii.

Pasul urmator consta in evaluarea modului in care consecintele acestor preconditii se propaga prin program. Cercetatorii au analizat diverse structuri de programe pentru a vedea cum este afectata executia lor de o anumita afirmatie despre care se stie ca este adevarata inainte de executia structurii respective. Daca, de exemplu, se stie ca afirmatia este adevarata inainte de executia structurii if (conditie)

then (instructiunea 1)

else (instructiunea 2)

atunci imediat inainte de executia instructiunii 1 putem spune ca atat afirmatia respectiva, cat si conditia de test sunt adevarate, in timp ce daca se executa instructiunea 2 stim ca sunt adevarate afirmatia respectiva si negarea conditiei de test.

Sa luam ca exemplu ciclul repeat din fig. 2.2.10.:

A Preconditii

Initializare

Corpul  buclei

B

Invariant

T e s t

C

Invariant si conditia de incheiere

Fig. 2.2.10. Asertiuni asociate cu o structura repeat

Sa presupunem ca in urma preconditiilor din pct. A putem stabili ca o anumita asertiune este adevarata de fiecare data cand in timpul procesului repetitiv este atins punctul B (o astfel de asertiune care apare in cadrul unui ciclu este cunoscuta sub numele de invariant al buclei). La incheierea procesului repetitiv, executia ajunge in punctul C, unde putem spune ca atat invariantul, cat si conditia de iesire sunt adevarate.

Invariantul este in continuare adevarat, deoarece testul de incheiere a ciclului nu modifica nici o valoare de program, iar conditia de incheiere este adevarata, pentru ca astfel ciclul nu s-ar terminat).

Daca aceste asertiuni combinate implica obtinerea rezultatului de iesire dorit, atunci pentru a demonstra ca astfel ciclul nu s-ar fi terminat.

Daca asertiunile de mai sus implica obtinerea rezultatului de iesire dorit, pentru a demonstra ca programul este corect trebuie sa aratam ca cele doua componente ale controlului, initializarea si modificarea, conduc la indeplinirea conditiei de incheiere.

Tehnicile formate de verificare a programelor nu au atins un stadiu care sa faciliteze aplicarea lor asupra sistemelor generale de prelucrare a datelor. In cele mai multe cazuri, programele sunt "verificate" prin aplicarea lor pe seturi de date de test, procedura care nu este foarte sigura. Alegerea datelor de test folosite pentru verificarea programelor ar trebui tratata cu aceeasi atentie ca si obtinerea unui esantion reprezentativ pentru o cercetare statistica.