MODELAREA CONCEPTUALA A DATELOR

Pentru definirea modelului conceptual al datelor se apeleaza la modele intermediare care sunt folosite ca suport al unei metodologii de proiectare. Un model conceptual este un ansamblu de concepte si reguli de combinare a acestor concepte permitand reprezentarea realitatii circumscrise domeniului supus informatizarii

Modelele utilizate se numesc modele semantice si au drept obiectiv ca prin conceptele oferite sa permita reprezentarea lumii reale.

Modelele semantice utilizeaza abstractii reprezentand lumea reala ca pe o colectie de entitati si de legaturi, stabilite intre acestea. Majoritatea modelelor permit definirea de restrictii descriind aspectele statice, dinamice sau chiar temporale ale entitatilor.

II-1 Modelul Entitate-Asociere (EA)

Modelul entitate-asociere (EA) pe care il vom utiliza in continuare pentru definirea modelului conceptual al datelor este si el un model semantic.

Modelul EA urmareste obtinerea unei reprezentari fidele, utilizand concepte specifice, a realitatii (problemei de rezolvat ce urmeaza a fi informatizata).

Aceasta reprezentare a lumii reale se va realiza facandu-se abstractie de orice restrictie fie ea informatica sau organizatorica. Pornind de la semantica obiectelor lumii reale si a legaturilor stabilite intre acestea modelul EA serveste in egala masura ca un mijloc de comunicare intre modelator (informatician) si viitorul utilizator al sistemului (beneficiarul sistemului informatic), care descrie realitatea supusa modelarii in conformitate cu propria lui perceptie.

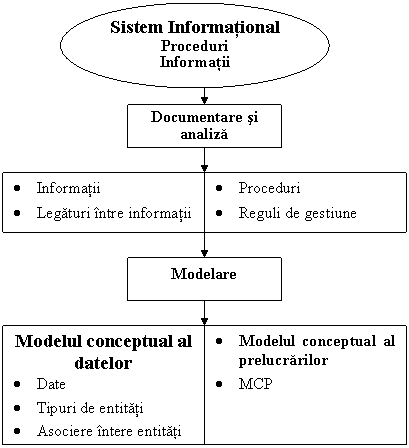
Fig.1)       Procesul de modelare a datelor si prelucrarilor

II-1.1) Concepte de baza ale modelului Entitate Asociere

II-1.1.1) ENTITATEA

Entitatea reprezinta un obiect al realitatii modelate caracterizat printr-o existenta proprie, cu o identitate proprie (care-l face identificabil in raport cu celelalte obiecte de acelasi tip) si o multime de caracteristici care exprima proprietatile acestuia.

Pentru exemplificare va propunem ca domeniu de studiu gestiunea politelor incheiate de o societate de asigurari. Entitatile pe care le putem defini sunt: o polita de asigurare, instrumente de plata, etc.

Entitatea polita de asigurare nr. 25 se defineste prin urmatoarele realizari ale caracteristicilor: 15/03/2002 (data incheierii), Ionescu Costel (numele agentului de asigurare), Popescu Marius (titularul politei de asigurare), 22/03/2002 (data inceperii perioadei asigurate), etc. Entitatea polita de asigurare nr. 25 are propria identitate, distingandu-se clar de celelalte entitati de acelasi tip (celelalte polite incheiate) prin numarul sau si are o existenta de sine statatoare (Figura 2.2).

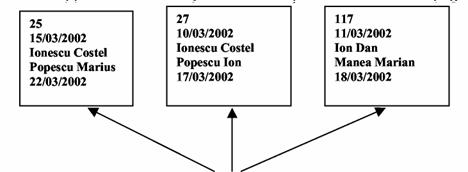
Fig.2)   Entitati apartinand tipului de entitate polita de asigurare

II-1.1.1.a) TIP DE ENTITATE

In activitatea de modelare interesul se focalizeaza pe definirea tipurilor de entitati apartinand problemei de rezolvat si nu pe entitati care reprezinta realizarile tipurilor de entitati. In locul notiunii de tip de entitate, unii autori folosesc conceptul de clasa de entitati. Modelul abstract pe care ni-l ofera modelul EA se bazeaza tocmai pe aceste tipuri generice de entitati si a legaturilor stabilite intre acestea.

Tipul de entitate reprezinta un concept generic desemnand multimea tuturor entitatilor prezentand aceleasi caracteristici constructive.

Fig.3)  

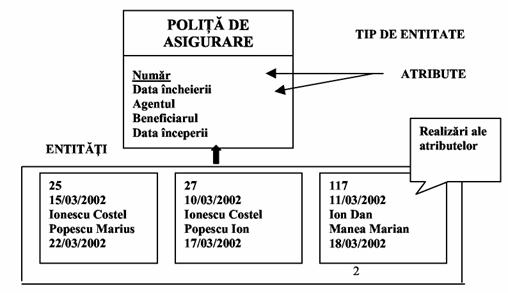
Entitati apartinand aceluiasi tip

Exemple : produs, comanda, angajat, student, contract, polita de asigurare, depozit bancar, ordin de tranzactionare la bursa etc.

Tipul de entitate 'Produs' desemneaza ansamblul produselor aflate in catalogul firmei, produse descrise plecand de la aceleasi caracteristici comune: codul produsului, denumirea, unitatea de masura, data omologarii, procent TVA.

Tipul de entitate 'Student' desemneaza ansamblul studentilor caracterizati prin aceleasi trasaturi comune: numar matricol, nume, data-nasterii, localitatea, facultatea, specializarea etc.

Atentionam asupra faptului ca o entitate poate apartine mai multor tipuri de
entitati diferite. De exemplu, entitatea cititorului Ionescu poate apartine si tipului de entitate profesor si tipului de entitate doctoranzi (desemnand ansamblul persoanelor care urmeaza forma de pregatire doctorala).

Fiecare tip de entitate se defineste prin multimea caracteristicilor comune entitatilor apartinand tipului.

II-1.1.1.b) ATRIBUTUL

ATRIBUTUL defineste o proprietate distincta a unei entitati. Fiecare atribut prezinta un domeniu, adica o multime de valori admise, intr-o entitate se regasesc realizari corespunzatoare caracteristicilor definitorii pentru tipul de entitate. Atributele pot fi clasificate in functie de mai multe criterii:

a)   Dupa complexitate atributele sunt:

elementare (simple) ale caror realizari nu pot fi descompuse (exemplu: unitate monetara, pret unitar, numar matricol al studentului, marca angajatului, etc).

decompozabile (complexe) ale caror realizari sunt decompozabile (ex: data calendaristica - se poate descompune in zi, luna, an; adresa - se poate descompune in strada, numar etc).

b)   Dupa realizarile pe care le pot prezenta atributele pot fi:

v           

obligatorii - trebuie sa prezinte obligatoriu o realizare, ceea ce corespunde sintagmei NOT NULL -
orice realizare.

optionale - sunt atribute care pot sa nu prezinte nici o valoare (realizare) in cadrul unei entitati (de exemplu atributele: telefon, fax, e-mail - nu toate persoanele au telefon, fax, adresa e-mail).

v           

monovaloare: atribute care prezinta o singura valoare in cadrul unei entitati (exemplu: nume
student, nr. matricol, data nasterii, codul numeric personal etc).

multivaloare: atribute care prezinta mai multe realizari in cadrul aceleiasi entitati (de exemplu, in tipul de entitate ANGAJAT, entitatea Popescu Marius poate prezenta pentru atributul STUDII mai multe valori: Facultatea de Mecanica, Facultatea de Finante Asigurari Banci si Burse de Valori).

II-1.1.1.c) Tipuri de obiecte. Obiecte simple, compozite si/ sau complexe.

Problema de modelat este adesea deosebit de complexa in cadrul ei putandu-se identifica obiecte simple, compozite si/ sau complexe.

In modelul EA obiectelor lumii reale le corespund entitati, iar entitatile definite prin aceleasi caracteristici formeaza un tip de entitate.

II-1.1.1.c.1) Obiecte simple

Aceasta inseamna ca obiectelor simple le va corespunde in modelul conceptual al datelor cate un tip de entitate.

Exemplu.       Pentru conturile deschise de o banca se poate defini in cadrul modelului conceptual al datelor tipul de entitate cont bancar (Figura 2.4).

Fig.4)   Tipul de entitate Cont Bancar

Clientilor (persoane fizice) ai unei banci, deoarece sunt definiti prin aceleasi caracteristici (nume client, cod numeric personal, cod de identificare in cadrul bancii, adresa etc), le va corespunde in modelul EA un singur tip de entitate, numarul de realizari ale acestuia (de entitati) fiind egal cu numarul clientilor.

II-1.1.1.c.2) Obiecte compozite

Obiectele compozite se caracterizeaza prin faptul ca ele contin una sau mai multe caracteristici multivaloare (carora in modelul EA le vor corespunde atribute multivaloare). Aceasta va determina ca in modelul conceptual optimizat al datelor acestui obiect compozit sa-i corespunda mai multe tipuri de entitati (atributele multivaloare se vor regasi intr-un tip de entitate distinct).

Exemplu.       Documentelor bonuri de consum le va corespunde tipul de entitate bon de consum definit prin atributele monovaloare: numar bon, data bon, sectia, gestiunea dar si atributele multivaloare: cod material, cantitate eliberata, pret unitar. Aceasta face ca tipul de entitate bon de consum, definit initial prin multimea tuturor atributelor mai sus mentionate, sa conduca in final la definirea a doua tipuri de entitati: Bon de consum (documentul in sine) definit prin atributele: numar bon, data bon, sectia, gestiunea si tipul de entitate Material eliberat definit prin atributele: cod material, cantitate eliberata, pret unitar (Figura 2.5).

Intr-un mod asemanator putem reprezenta in modelul EA facturile, comenzile emise de clienti pentru livrarea produselor etc.

Fig.5)  

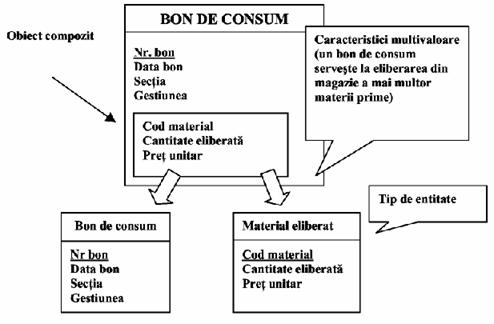
Reprezentarea obiectelor compozite sub forma de tipuri de entitati

II-1.1.1.c.3) Obiecte compuse

Obiectele compuse sunt decompozabile ele regrupand in structura lor obiecte simple intre care exista o anumita legatura. Chiar daca in modelul EA initial pentru un obiect compus s-a definit un singur tip de entitate, ulterior acesta se va descompune in tipuri de entitati de sine statatoare corespunzatoare obiectelor elementare care intra in structura obiectului compus (Figura 2.6).

Exemplu.       Tipul de entitate contract de credit - definit prin atributele: numar contract, data contract, titular, valoare contract, unitate monetara, garantii - corespunde unui obiect compus al realitatii de modelat. Titularul si garantia sunt doua obiecte distincte ale problemei de modelat, fiecaruia trebuind sa-i corespunda in MCD un tip de entitate distinct. Ca urmare, se vor include in MCD tipurile de entitati:

TITULAR definit prin: Cod identificare, nume, cod numeric personal, adresa, data nasterii.

GARANTIE care poate fi reprezentata, de exemplu, de o scrisoare de garantie bancara definita prin atributele: numar document, data emiterii, banca emitenta, termen de valabilitate, suma.

CONTRACT DE CREDIT definit prin: Nr. Contract, Data contract, Valoare contract, Moneda.

Fig.6)  

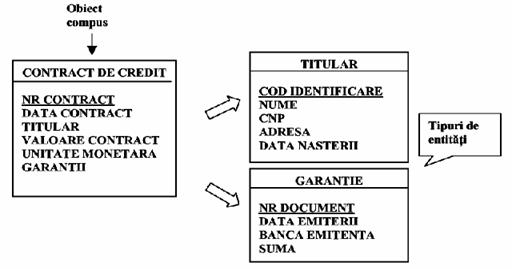
Reprezentarea obiectelor compuse sub forma de tipuri de entitati

II-1.1.1.d) IDENTIFICATOR

Fiecare tip de entitate prezinta un identificator reprezentat de un atribut sau un grup minimal de atribute al carui rol este de a permite identificarea in mod unic, fara echivoc, a entitatilor.

De multe ori identificatorul este reprezentat de un atribut de tip 'numar de ordine' (incrementat cu 1 pentru fiecare noua valoare atribuita) sau de un cod (constructie artificiala avand o anumita semnificatie).

Exemplu.       Pentru:

tipul de entitate STUDENT identificatorul va fi Nr Matricol;

in cazul entitatii BON CONSUM identificatorul va fi atributul Nr. Bon (atribut de tip numar de ordine), etc.

In reprezentarea grafica a tipului de entitate identificatorul este marcat distinct prin subliniere (Figura II.7)

Fig.7)   Tipul de entitate Student

II-1.1.2) ASOCIEREA

Asocierea dintre entitati exprima legatura stabilita dintre acestea si rolul pe care il joaca fiecare entitate participanta la legatura.

Exprimand o legatura dintre entitati ea nu are o existenta de sine statatoare. O asociere poate prezenta unul sau mai multe atribute proprii cu rol de a caracteriza, explicita, legatura stabilita intre entitatile participante la asociere.

Exemplu.       Atributele Data debut si Data sfarsit caracterizeaza asocierea Ocupa si aceasta deoarece ele nu sunt proprietati ale entitatii Camere - aceiasi camera cu nr. 10 poate fi ocupata la date diferite de catre clienti diferiti. Fiecare entitate participanta la asociere joaca un anumit rol. In exemplul prezentat in figura II.8 entitatea Client joaca rolul ocupant (clientul x ocupa in data y camera z) iar entitatea Camera prezinta rolul este ocupata (camera z este ocupata in data y de clientul x).

II-1.1.2.a) TIPUL DE ASOCIERE

Tipul de asociere se defineste ca ansamblul legaturilor, prezentand aceiasi semnificatie, dintre entitatile apartinand la doua sau mai multe tipuri de entitati. Exemplu: tipul de asociere Ocupa din figura 2.8.

Fig.8)  

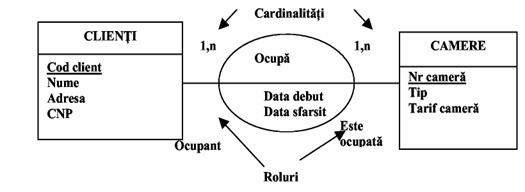
Tipul de asociere Ocupa

II-1.1.2.b) CARDINALITATEA

Cardinalitatea cuplului entitate-asociere reprezinta cuplul de valori intregi (x,y) astfel incat:

x - cardinalitate minimala exprima numarul minim de realizari ale legaturii (asocierii) care pot exista pentru o entitate

y - cardinalitate maximala reprezinta numarul maxim de aparitii ale corespondentei care pot exista pentru o entitate;

v   Cardinalitatea minimala 0 (zero) indica faptul ca pot exista anumite entitati ale unui tip de entitate care sa nu participe la nici o asociere.

Exemplu.       Exista clienti potentiali ai unei firme carora inca nu li s-au incheiat polite de asigurare - cardinalitate minimala 0, dar sunt clienti carora li s-au incheiat mai multe polite - cardinalitate maximala n.

Fig.9)  

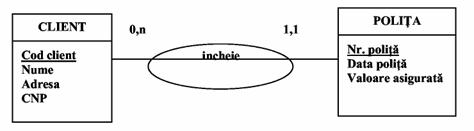
Cardinalitatea minimala 0 si 1

v   Cardinalitatea minimala 1 indica faptul ca toate realizarile tipului de entitate trebuie sa participe la cel putin o realizare a tipului de asociere.

Exemplu.       Orice contribuabil aflat in evidenta administratiei financiare are deschis un rol fiscal si numai unul singur (in acest caz atat ccardinalitatea minimala cat si cea maximala sunt 1).

v  

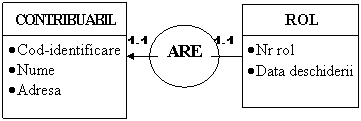
Cardinalitatea maximala 1 indica faptul ca numarul de roluri fiscale deschise unui contribuabil la administratiafinan financiara nu poate fi mai mare de 1

Sageata din figura 2.10 indica caracterul imuabil al asocierii (rolul fiscal nu-si modifica titularul).

Fig.10)   Cardinalitatea maximala 1

v   Cardinalitatea maximala N indica faptul ca unele entitati ale unui tip de entitati pot participa la mai multe de o asociere.

Exemplu.       Un client (Figura 2.11). poate emite 0 sau mai multe documente de plata. Deci cardinalitatea dintre entitatea client si  asocierea emite este

minimala

maximala=N

De asemenea un document poate fi emis numai si numai catre un client si odata emuis nu se mai poate modifica (vezi sageata). In acest caz, atat cardinalitatea minimala cat si aceea maximala sunt 1.

Fig.11)   Cardinalitatea maximala N

Uneori valoarea lui N poate fi specificata clar printr-o constanta.

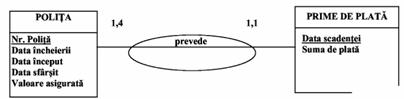
Exemplu.       Pentru o polita de asigurare (incheiata pe un an) sunt calculate maxim 4 prime de asigurare - cate una pe trimestru (figura 2.12).

Fig.12)   Cardinalitatea maximala 4

Valorile uzuale pentru exprimarea cardinalitatii sunt: 0,1; 1,1; 0,n; 1,n.

Intre realizarile a doua tipuri de entitati se pot stabili mai multe asocieri prezentand semantica diferita si prin urmare cardinalitati diferite.

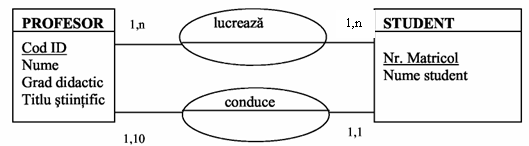
Exemplu.       Un profesor lucreaza la o disciplina cu un grup de studenti, unora dintre acestia (maxim 10) conducandu-le si proiectul de semestru la disciplina respectiva (figura 2.13).

Fig.13)            

Referitor la structura tipurilor de asocieri putem sintetiza astfel:

Asocierea poate avea atribute

Legatura dintre o asociere si o entitate se caracterizeaza prin

Rolul jucat de entitate in asociere;

Cardinalitatea legaturii dintre asociere si entitate;

II-1.1.2.c) Tipuri de asocieri intre entitati

Exista trei tipuri posibile de asocieri intre entitati, functie de numarul de tipuri de entitati participante la asociere. Acestea sunt:

unara (refexiva)

binara

complexa

Asocierea reflexiva (ciclica, unara) se caracterizeaza prin faptul ca exprima legaturile stabilite intre entitati apartinand aceluiasi tip (figura 2.14).

Fig.14) 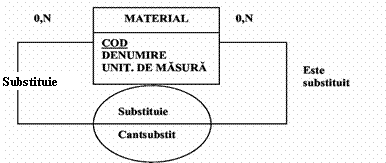      Asocire reflexiva

Exemplu.       O materie prima necesara pentru fabricarea unui produs poate fi substituita (daca nu exista cantitatea necesara in stoc) printr-o alta materie prima (avand aceleasi caracteristici dar spre exemplu o alta concentratie) intr-o anumita cantitate.

Asocierile binare reprezinta legaturi (corespondente) stabilite intre realizarile apartinand la doua tipuri de entitati diferite.

Exemplu.       Asocierea Prevede stabilita intre tipul de entitate POLITA si tipul de entitate PRIMA DE PLATA (figura 2.12) sau asocierile Lucreaza si Conduce din figura 2.13.

Asocierile complexe exprima legaturi stabilite intre realizarile mai multor tipuri de entitati. Spre exemplu, o asociere ternara se poate stabili intre tipurile de entitati: CONTRIBUABIL, TAXA, DOCUMENT DE PLATA .

Fig.15)  

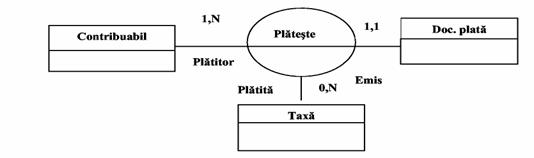
Asociere ternara

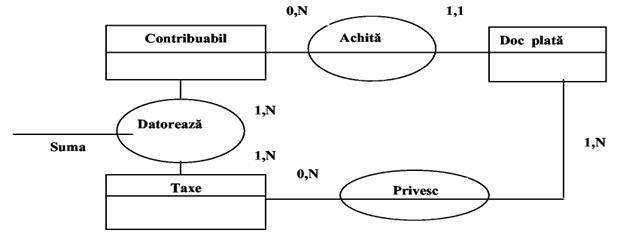
Se recomanda insa reducerea acestor asocieri complexe la asocieri binare. Astfel asocierea ternara prezentata in figura 2.15 se descompune conform figurii 2.16 in asocieri binare.

In continuare prezentarea se va referi doar la asocierile binare.

Fig.16)   Descompunerea unei asocieri ternare in asocieri binare

II-2 Restrictii de integritate

Restrictiile de integritate definesc cerintele pe care datele trebuie sa le respecte pentru a fi corecte si coerente in raport cu realitatea pe care o reflecta

Restrictiile de integritate reprezinta o modalitate de integrare a semanticii datelor in mod indirect in modelul EA pe care astfel il imbogatesc.

Restrictiile de integritate privesc:

valorile pe care le pot lua atributele entitatilor si asocierilor;

valorile identificatorilor entitatilor;

rolurile jucate de entitati in asocierile la care participa;

asocierile stabilite intre entitati

Pentru modelul EA prezentat in Figura II-17 pot fi definite urmatoarele restrictii de integritate privitoare la valorile pe care le pot lua atributele (tipul 1 de integritate):

data documentului (comenzii) sa fie anterioara datei curente sau egala cu aceasta;

cota de TVA poate fi 0%, sau 19%;

produsul cel mai vechi din nomenclatorul de fabricatie a fost omologat in 12.12.99

unitatile de masura sunt KG si BUC.

numarul gestiunii poate lua valori in multimea M=;

tipul depozitului poate fi frigorific/nefrigorific;

Fig.17) 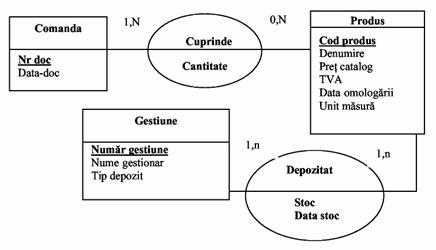  Model EA

Restrictiile de integritate pot fi:

statice - se verifica permanent;

dinamice - privesc evolutia in timp a datelor;

Exemplu.       Restrictiile referitoare la numarul gestiunii, tipul depozitului si unitatile de masura sunt statice. Restrictia privind cota de TVA este dinamica ea putandu-se modifica in timp in conformitate cu prevederile fiscale in vigoare.

II-2.1) Restrictii de domeniu

Domeniul reprezinta multimea de valori pe care le poate lua un atribut. El poate fi definit

printr-o proprietate (o conditie privind un atribut sau un grup de atribute);

prin precizarea unui interval de valori;

prin enumerarea multimii de valori admise;

Restrictiile de domeniu reprezinta conditii (reguli) care privesc ansamblul de valori admise pentru un atribut in cadrul tipului sau domeniului sau.

Restrictiile de domeniu pot fi:

restrictii intraentitate - care se refera la realizarile unui/unor atribute apartinand unei aceleiasi entitati sau asocieri

restrictii interentitati - care se refera la realizarile unui/unor atribute apartinand unor entitati si/sau asocieri diferite

Restrictiile pe domeniu se pot exprima cu privire la:

Continutul unui singur atribut al unei entitati sau asocieri:

Exemplu.      

Unit. Masura=

TVA =

Pret > 10.000 si pret < 10.000.000

Cantitate > 10 (cantitatea este un atribut definit pentru asocierea CUPRINDE din Figura 2.17).

Corelatiile ce trebuie sa se respecte intre valorile mai multor atribute sau asocieri
apartinand aceleiasi entitati sau asocieri:

Exemplu.      

Numar gestiune=1 atunci nume gestionar = 'Ion Toma'

Cod produs=12 atunci Unit Masura='BUC'

Corelatiile care trebuie sa existe intre atributele apartinand mai multor entitati sau asocieri diferite:

Exemplu.      

in gestiunea 1 se stocheaza doar produsele avand codurile in multimea .

Data-stoc > data omologarii

Cod produs=112 atunci numar gestiune=1

Corelatii realizate pe baza unor valori obtinute prin operatii de sintetizare (insumare, calculul mediei, valorii minime /maxime etc.) a unui ansamblu de entitati:

Exemplu.      

Suma cantitatilor comandate pentru un produs nu poate depasi stocul din data respectiva.

Pretul mediu al produselor >200.000

II-2.2) Restrictii structurale

v            Identificarea entitatilor

Fiecare entitate va trebui sa poata fi identificata fara echivoc. Acest lucru impune ca identificatorul entitatii sa ia valori unice si diferite de NULL (NULL inseamna ca nu s-a atribuit nici o valoare valoarea NULL este diferita de zero sau spatiu).

In definirea modelului EA putem intalni cazuri mai speciale legate de identificarea entitatilor:

Nu putem defini un identificator sub forma unui atribut /grup de atribute pentru un anumit tip de entitate (Figura 2.18). 

Exemplu.       Pentru fiecare angajat al firmei se consemneaza lunar prezenta prin precizarea orelor efectiv lucrate, orelor absentate, orelor de concediu si de concediu medical.

Identificarea entitatilor Prezenta se face prin rolul Realizeaza pe care entitatea Angajat il joaca in asocierea Inregistreaza

Identificarea prin rol a entitatilor se poate realiza doar daca asocierea in cauza nu este ciclica (unara) iar cardinalitatea cuplului entitate identificata-asociere este (1,1) si cardinalitatea cuplului entitate identificator - asociere este ( sau (0, 1).

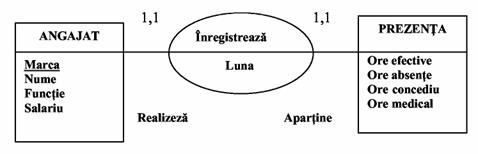
Fig.18)  

Identificarea unei entitati se poate realiza prin unul sau mai multe atribute proprii impreuna cu rolul jucat de alt tip de entitate (figura 2.19) in cadrul asocierii.

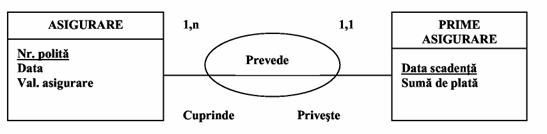
Fig.19)  

O polita de asigurare de viata presupune pe langa specificarea numarului, datei incheierii politei, valorii asigurate si precizarea primelor de plata cu inscrierea datei limita a platii precum si a sumei de plata (consideram ca sumele sunt diferite de la o scadenta la alta). Fiecare polita se identifica prin numar, atribuit in mod unic. Pentru tipul de entitate Prime asigurare, atributul Data scadentei nu poate fi identificator deoarece, la aceeasi data mai multe polite au acelasi termen limita de plata. Identificarea entitatilor Prime asigurare se va realiza prin valorile atributului propriu Data scadentei si rolul Cuprinde jucat de entitatea Asigurare in asocierea Prevede.

II-2.3) 2.2.3. Restrictii de integritate de roluri

In definirea asocierii am subliniat faptul ca aceasta exprima legatura stabilita intre entitati diferite, fiecare dintre acestea jucand un anumit rol.

Restrictia de integritatea de roluri se refera la faptul ca daca o entitate are un anumit rol intr-o asociere, atunci acest rol va implica anumite conditii si asupra altor roluri jucate de respectiva entitate cu alte asocieri.  Plecand de la rolurile jucate de entitati in cadrul asocierilor putem defini o serie de restrictii de integritate si anume de : egalitate, incluziune si excluziune de roluri.

v            Restrictia de incluziune de roluri

Restrictia de incluziune de roluri statueaza faptul ca, daca o entitate E1 care joaca rolul r1 in asocierea A1 va trebui sa joace si rolul r2 in asocierea A2. Rezulta ca rolul r1 include (implica prin incluziune) rolul r2.

Pentru reprezentarea restrictiei de incluziune de roluri se va utiliza urmatoarea reprezentare grafica:

Fig.20)   Incluziune de roluri

Exemplu.       Secventa de MCD elaborat pentru o firma de asigurari. (Figura 2.21).

Clientii incheie polite de asigurare si primesc despagubiri la producerea riscului asigurat daca au la zi plata primelor de asigurare.

Intre rolul despagubita si rolul achitata se manifesta o restrictie de incluziune de rol.

De asemenea este o restrictie de integritate pe rolurile despagubita si incheiata pe care le joaca entitatea polita.

Fig.21)   Incluziune de roluri

v            Restrictia de egalitate de roluri

Egalitatea de roluri presupune ca restrictia de incluziune intre roluri sa fie reciproca.

Grafic restrictia de egalitate de roluri se reprezinta conform figurii rl

Fig.22)   Egalitatea de roluri

Persoanele care au un rol (fisa) deschis la administratia financiara, deci joaca rol de posesor in asocierea Are, inseamna ca au obligatii fiscale, deci joaca rol de contribuabil in asocierea Datoreaza, reciproca fiind valabila: orice persoana care are obligatii fiscale trebuie sa aiba deschis un rol. Dar nu toate persoanele sunt contribuabili, deci exista entitati ale tipului Persoana care nu joaca rolul de Posesor in asocierea Are. Grafic, egalitatea de roluri se reprezinta conform figurii 2.23.

Fig.23)  

Egalitate de roluri

v            Restrictia de excluziune de roluri

Excluziunea de roluri specifica faptul ca un rol r1 jucat de o entitate E1 in asocierea A1 exclude existenta rolului r2 jucat in asocierea A2.

Fig.24)  

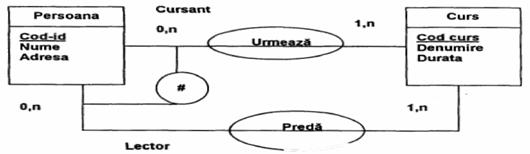
Reprezentarea excluziunii de roluri

Fig.25)   Excluziunea de roluri

Din exemplele prezentate rezulta ca restrictiile de integritate de roluri vizeaza rolurile pe care o entitate le poate juca in cadrul unor asocieri diferite.

Incluziunea de roluri specifica faptul ca un rol r2 jucat de entitatea E1 in asocierea A2 este urmarea rolului r1 jucat de aceeasi entitate in asocierea A1.

Restrictia de egalitate de roluri evidentiaza ca rolul r1 jucat de entitatea E1 in asocierea A1 determina rolul r2 jucat de aceeasi entitate in asocierea A2, iar rolul r2 determina in acelasi timp rolul r1.

Restictia de excluziune de roluri precizeaza ca, daca o entitate E1 joaca rolul r1 in asocierea A1 nu poate juca rolul r2 intr-o alta asociere numita A2.

Dar aceste restrictii legate de participarea entitatilor la asocieri nu pot fi judecate doar la nivel de roluri ci este necesara uneori precizarea unor restrictii de integritate la nivelul tipului de asociere, deci a ansamblului de asocieri prezentand aceeasi semantica.

II-2.4) 2.2.4. Restrictii de integritate de asocieri

Restrictiile analizate in  acest subcapitol vizeaza asocierea insasi impreuna cu entitatile participante. Altfel spus restrictiile se refera la multimea tuturor rolurilor apartinand asocierii.

v            Restrictia de incluziune de asocieri

Restrictia de incluziune exprima faptul ca asocierea A1 stabilita intre doua entitati va determina existenta unei alte asocieri A2 in cadrul modelului EA.

Exemplu.       Un broker primeste ordine de la clientul sau si executa tranzactii.

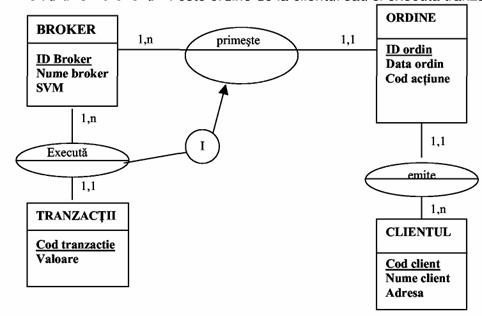
Fig.26)   Incluziunea de asocieri

Tipul de asociere executa este determinat de existenta tipului de asociere primeste (brokerul nu poate efectua tranzactia daca nu a primit ordinul corespunzator).

v            Restrictia de excluziune de asocieri

Restrictia de excluziune de asocieri exprima faptul ca asocierile apartinand tipului de asociere A1 exclud asocierile apartinand tipului A2.

Exemplu.       Studentii din universitatile de stat care achita taxa de scolarizare nu pot fi bursieri ai acestor institutii. Rezulta ca intre Achita (taxe) si incaseaza (bursa) este o excluziune de asocieri.

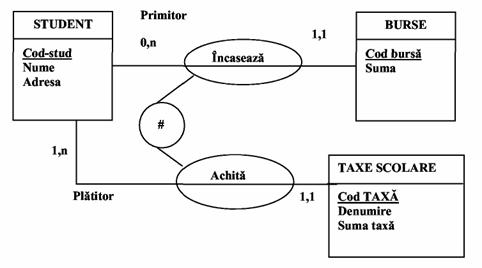
Fig.27)   Excluziune de asocieri

v            Restrictia de egalitate de asocieri

Restrictia de egalitate de asocieri exprima faptul ca asocierile apartinand tipului A1 determina existenta asocierilor apartinand tipului A2 si invers. Exemplu:

Fie tipurile de entitati Carti si Legitimatii intre care se stabilesc tipurile de asocieri Poseda si Imprumuta cu tipul de entitate Student. Intre aceste asocieri se stabileste o restrictie de egalitate de asocieri deoarece orice imprumut de carte implica posesia legitimatiei de acces la biblioteca iar posesia legitimatiei implica posibilitatea imprumutului de carte (Figura 2.28). Toate rolurile Cititor implica toate rolurile Posesor si entitatile participante la asociere.

Fig.28)   Restrictie de egalitate de asocieri

II-3 Dependente functionale

II-3.1) Tipuri de dependente functionale

Conceptul de dependenta functionala (DF) este fundamental in analiza structurii datelor. Studiul dependentelor functionale stabilite intre atribute ne permite obtinerea unei reprezentari formalizate a structurii de date.

Dependentele functionale evidentiaza raporturile de determinare stabilite intre atributele unei entitati.

O dependenta functionala pune in relatie doua atribute: determinantul si determinatul.

Fig.29)   Dependenta functionala

Aceasta DF subliniaza faptul ca unei realizari a atributului Nr. rol ii va corespunde intotdeauna aceeasi realizare a atributului Nume contribuabil, iar aceeasi realizare a atributului Cod fiscal va fi asociata aceluiasi Agent economic.

Rezulta ca determinantul reprezinta atributul/grupul de atribute din stanga DF care prin valoarea sa determina valoarea luata de atributul cu rol de determinat.

Fie tipul de entitate R si A,B,C atributele apartinand lui R, iar X, Y, Z ansamblurile de realizari ale atributelor lui R. Spunem ca in tipul de entitate R se verifica DF: X àY daca in doua realizari ale lui R avand aceleasi valori pentru X exista aceleasi valori pentru Y.

Rezulta deci ca DF este o relatie de determinare stabilita intre atributele apartinand aceluiasi tip de entitate.

Daca valorile atributelor cuprinse in Y sunt cunoscute, atunci ele sunt in functie de valorile atributelor apartinand lui X pentru ca ele sunt determinate in mod unic de acestea din urma.

v            Tipurile de dependente functionale sunt

Dependenta functionala elementara sau compusa (neelementara), adica o DF poate implica atribute sau grupuri de atribute.

Daca: A à(B,C) atunci exista dependentele functionale: AàB si AàC

Exemplu.       DF Nr. Politaà(Data polita, Nume agent) Ne conduce la identificarea dependentelor functionale:

Nr. Polita àData polita

Nr. Polita àNume agent

Totusi trebuie precizat urmatorul aspect: daca exista o DF: (A,B) àC aceasta nu inseamna ca se verifica dependentele functionale: AàB si AàC

Exemplu.       Daca exista DF: (Cod-material, cod-furnizor) àpret-aprovizionare, aceasta inseamna ca pret-aprovizionare nu depinde numai de codul materialului ci si de furnizor, acelasi material putand fi aprovizionat la preturi diferite de la furnizori diferiti.

Dependenta functionala completa.

DF XàY este o dependenta functionala completa daca Y este dependent functional de X fara sa fie dependent functional de nici o alta din componentele lui X (pretul de aprovizionare este determinat atat de furnizor cat si de materialul aprovizionat).

Dependenta functionala partiala

DF XàY se numeste dependenta functionala partiala daca Y este dependent functional atat de X cat si de o parte a lui X.

Exemplu.       Fie tipul de entitate E definit prin atributele: cod operatie, cod reper, timp-prelucrare, categorie-operatie. Intre atributele apartinand lui E exista urmatoarele DF

Cod operatie, cod reper àtimp de prelucrare (DF completa)

Cod operatie, cod reper àcategorie-operatie (DF partiala)

Dependenta functionala triviala

DF XàY se numeste dependenta functionala triviala daca Y X

Dependenta functionala tranzitiva

In procesul de analiza a datelor pot fi identificate DF tranzitive

DF XàA este o dependenta functionala tranzitiva daca

A este un atribut unic neinclus in X astfel incat exista Y X, XàY si YàA si Y nu determina X.

Exemplu.       Sa analizam dependentele functionale care se stabilesc intre atributele: CNP (cod numeric personal), Nume persoana, Localitatea de domiciliu, Cod localitate apartinand tipului de entitate Persoana. CNP fiind ales drept identificator al entitatii inseamna ca exista dependentele functionale:

CNP àNume persoana

CNP àLocalitatea de domiciliu

CNP àCod localitate

Dar mai exista DF

Localitate de domiciliu àCod localitate - ceea ce ne conduce la concluzia ca

DF: CNP àCod localitate este o DF tranzitiva.

Dependenta functionala multivaloare

Dependenta functionala multivaloare se manifesta atunci cand valorii unui atribut/grup de atribute ii corepund mai multe valori ale unui alt atribut. DF multivaloare se reprezinta astfel:

X èèY

O dependenta multivaloare poate sa se manifeste in cazul unei entitati prezentand cel putin trei atribute (A,B,C) astfel incat:

A determina mai multe valori pentru B;

A determina mai multe valori pentru C;

B si C sunt independente unul de celalalt;

Exemplu.       Sa presupunem ca dorim sa retinem informatia referitoare la numarul de inventar al mijloacelor fixe aflate intr-o sectie si marcile (codul de identificare) salariatilor care lucreaza in sectia respectiva intr-un tip de entitate numit SECTII al carui identificator este atributul cod sectie. Se identifica intre aceste atribute dependentele functionale multivaloare:

Cod sectie èè Marca

Cod sectie èè Nr inventar

II-3.2) Proprietatile dependentelor functionale

Proprietatile dependentelor functionale, numite si regulile lui Amstrong sunt:

Reflexivitatea:

Daca Y X atunci se verifica DF: XàY unde X si Y sunt atribute/grupuri de atribute apartinand tipului de entitate R.

Dezvoltarea:

Pentru orice Z R daca se verifica X à Y atunci se verifica si DF: XZ à YZ

Tranzitivitatea:

Daca se verifica DF: XàY si DF: YàZ atunci este adevarata si DF: XàZ

Aditivitatea:

Daca exista DF: XàY si DF: XàZ atunci exista DF: XàYZ.

Pseudotranzitivitatea:

Daca exista DF: XàY si DF: WYàZ atunci se verifica DF: XWàZ.

Descompunerea:

Daca se verifica DF: XàY atunci se verifica si DF: XàZ daca Z Y

Studiul dependentelor functionale se poate realiza utilizand mai multe instrumente, in cele ce urmeaza ne propunem sa prezentam doua dintre acestea: matricea dependentelor functionale si diagrama dependentelor functionale care s-au dovedit complementare.

II-3.3) Matricea dependentelor functionale

Matricea dependentelor functionale poate fi realizata in doua variante:

matricea simplificata

matricea completa

Matricea simplificata reprezinta un tablou in care coloanele cuprind determinantii dependentelor functionale iar fiecare linie un atribut apartinand multimii atributelor supuse modelarii.

Matricea completa reprezinta un tablou asemanator matricii simplificate cu singura deosebire ca numarul de coloane este egal cu numarul liniilor, cu alte cuvinte antet de coloana va fi orice atribut (regasit si ca antet de linie) si nu doar atributele (grupurile de atribute) cu rol de determinant intr-o dependenta functionala.

Exemplu.       Matricea simplificata a dependentelor functionale

Sa elaboram matricea simplificata a dependentelor functionale pentru atributele necesare elaborarii MCD privind consumul normat de materii prime stabilit pentru produsele din nomenclatorul de fabricatie al firmei.

Multimea atributelor corespunzatoare problemei studiate este formata din: cod produs, denumire produs, cod um, pret livrare, cod reper, denumire reper, cantitate reper (in realizarea unui produs finit intra mai multe repere de acelasi fel sau diferite), cod material, denumire material, cantitate normata pe reper, denumire um. Pe baza multimii atributelor enuntate se identifica dependentele functionale stabilite intre acestea care apoi sunt marcate in matricea simplificata a dependentelor functionale.

Fig.30)   Matricea simplificata a DF

Analizand Figura 2.30 constatam ca fiecare coloana din matrice a fost rezervata unui determinant (se poate stabili anterior o lista a DF).

Valoarea 1 marcheaza la intersectia unei coloane cu o linie existenta unei DF intre atributul cu rol de determinant precizat in coloana si atributul determinat inscris la nivelul liniei.

Una din regulile modelului EA specifica unicitatea atributelor adica obligativitatea ca un atribut sa apartina unei singure entitati sau asocieri.

Plasarea unui atribut intr-o entitate sau alta este determinata de DF la care participa in legatura cu identificatorul tipului de entitate. Aceasta inseamna ca la nivelul matricei dependentelor functionale la nivelul fiecarei linii va trebui sa fie inscrisa o singura valoare 1.

In mod distinct, prin subliniere, in cadrul matricei au fost marcate cateva valori 1. Ele exprima proprietatea de reflexivitate a DF si sunt marcate la intersectia coloanei cu linia corespunzatoare acelorasi atribute (in cazul nostru determinantii).

O problema apare in liniile 3 si 8 unde cod um si cod material prezinta mai multi determinanti. Aceasta situatie atentioneaza asupra necesitatii unei analize si impune alegerea corecta a determinantului dependentelor functionale puse in evidenta. Existenta mai multor valori 1 pe o linie poare fi si consecinta unor DF tranzitive care pun in evidenta asocieri ierarhice (numite si restrictii de integritate functionala) intre entitatile ale caror identificatori sunt in dependenta functionala.

Exemplu.       Matricea completa a dependentelor functionale

In cazul matricei complete numarul de coloane corespunde cu numarul liniilor.

Fig.31)   Matricea completa a DF

Din analiza matricei complete a DF constatam:

diagonala de valori 1 rezultata (asa cum am precizat si in cadrul matricei simplificate) este consecinta proprietatii de reflexivitate a DF

existenta dependentelor elementare (prezentand un determinant elementar, format dintr-un atribut);

existenta dependentelor neelementare al caror determinant este format dintr-un grup de atribute. In cazul nostru (Cod produs, cod reper) si (cod reper, cod material).

existenta unor dependente tranzitive (cod produsàcod material) si multivaloare intre atributele cod produs si cod reper, respectiv intre cod reper si cod material care conduc la aparitia mai multor valori
in cadrul liniilor matricei.

Analiza informatiei din matrice (completa sau simplificata) ne va conduce la definirea unor tipuri de entitati optimizate in cadrul carora sa fie eliminate DF complexe.

II-3.4) Diagrama dependentelor functionale

Diagrama dependentelor functionale reprezinta un graf constituit pe baza DF identificate, pornind de la care vom putea defini tipurile de entitati ale modelului EA astfel incat in cadrul acestora sa nu se mai manifeste DF complexe. Notatiile pe care le vom utiliza in cadrul diagramei sunt:

Cvasi dependentele functionale sunt cele pentru care cunoasterea unei valori pentru determinant nu antreneaza sistematic cunoasterea unei valori a determinatului. De exemplu:

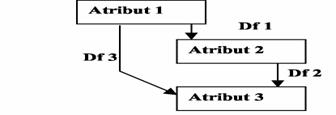
De multe ori aceste cvasi dependente functionale sunt reciproce. Un produs este format din mai multe repere dar un anumit reper participa la realizarea mai multor produse.

Un graf al DF pune in evidenta DF tranzitive:

Fig.32)   Graf al DF tranzitive

Dependenta tranzitiva DF3 va trebui eliminata din diagrama dependentelor functionale.

In cazul problemei pe care o avem de rezolvat cvasi dependente functionale reciproce sunt:

Dar dependenta functionala dintre atributul cod produs si atributul cod material este tranzitiva si va trebui eliminata din diagrama DF.

Pornind de la multimea atributelor ce definesc problema de rezolvat (enumerate in paragraful anterior) putem identifica dependentele functionale pe care le vom grupa in cadrul diagramei in functie de determinantii pe care ii prezinta.

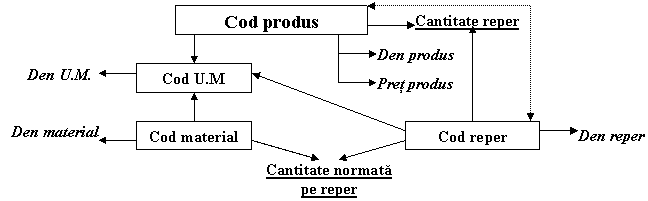
In aceste conditii diagrama DF va arata astfel:

Fig.33)   Diagrama DF

v            Trecerea de la diagrama dependentelor functionale la modelul EA se realizeaza pe baza urmatoarelor reguli:

Pentru fiecare DF in care determinantul este elementar se creeaza un tip de entitate in care determinantul DF joaca rolul de identificator.

In cazul problemei de rezolvat se vor defini patru tipuri de entitati si anume: Produs, Reper, Material si Unitati masura prezentand drept identificatori atributele: Cod produs, Cod reper, Cod material si respectiv Cod UM (Figura 2.34).

Fig.34)   Tipuri de entitati definite.

Toate atributele participand la dependente functionale ce prezinta acelasi determinant se vor grupa in cadrul aceluiasi tip de entitate prezentand drept identificator atributul cu rol de determinant in cadrul dependentelor functionale.

In urma aplicarii acestei reguli obtinem:

Fig.35)   Gruparea atributelor pe tipuri de entitati

Fiecarei dependente functionale intre identificatorii tipurilor de entitati ii va corespunde in modelul EA un tip de asociere. Exista doua feluri de asocieri, astfel

Asociere este ierarhica (restrictie de integritate functionala) atunci cand cardinalitatea maximala pentru cuplul E1A este 1 iar pentru cuplul E2A este N.

Aplicand aceasta regula obtinem:

Fig.36)   Definirea tipurilor de asocieri

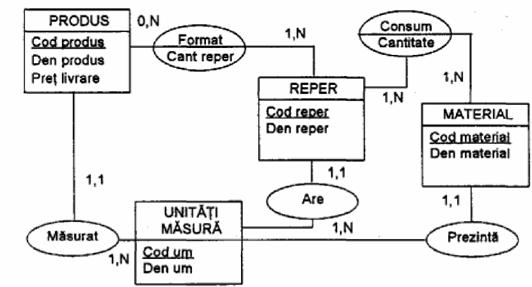
Asocierea este de tip neierarhic (restrictie de integritate multipla), atunci cand DF este neelementara (cu determinantul format dintr-un grup de atribute, care sunt identificatori in cadrul tipurilor de entitati definite). Acest tip de asociere neierarhica va fi definita prin atributul cu rol de determinat (in exemplu: cantitate reper sau cantitate normata pe reper) in DF. Aplicand regula obtinem:

Fig.37)   Model EA

Realizand  matricea simplificata a DF vom constata respectarea cerintelor de validare a modelului EA

Fig.38)   Matricea simplificata a DF

Matricea s-a realizat pe baza DF manifestate in cadrul tipurilor de entitati definite.

Se observa ca prin eliminarea elementelor de tranzitivitate pe fiecare linie a matricei ramane, asa cum este corect, o singura valoare semnificand ca un atribut prezinta un singur determinant.

II-4 Reguli de verificare si normalizare a MCD

II-4.1) Reguli de verificare a MCD

Realizarea MCD impune respectarea urmatoarelor reguli:

Regula de unicitate a numelor se aplica tuturor elementelor care participa la definirea MCD: tipuri de entitati, tipuri de asocieri,  atribute, roluri. Aceasta regula impune eliminarea din model a omonimelor si sinonimelor. Aceasta inseamna ca nu vom putea da, in cadrul aceluiasi MCD, si unui
atribut si unui tip de entitate acelasi nume, de exemplu Student. Vom numi tipul de entitate Student iar
atributul va primi denumirea Nume Student.

Regula unicitatii atributelor (neredundantei) impune ca un atribut sa defineasca un singur tip de entitate sau un singur tip de asociere.

Regula de unicitate a asocierilor, aplicabila in cazul asocierilor neierarhice, specifica faptul ca pentru fiecare realizare a asocierii nu poate sa existe decat o singura realizare a fiecarei entitati
participante la asociere.

Regula proprietatilor si determinantului unei entitati precizeaza ca un atribut care este determinat de mai multi determinanti, acestia fiind identificatori ai unor tipuri de entitati diferite, trebuie sa defineasca tipul de asociere creat intre respectivele tipuri de entitati.

Regula atributelor derivabile recomanda evitarea includerii in MCD a atributelor rezultate din calcule. Prezenta unor astfel de atribute in MCD se justifica numai daca ele sunt purtatoare ale unei informatii cu o anumita relevanta si frecventa de utilizare.

Regula atributelor decompozabile precizeaza ca pot fi mentinute in cadrul MCD atribute complexe in masura in care prelucrarile nu impun descompunerea lor pe componente elementare. Un exemplu este reprezentat de atributul adresa care se poate descompune pe urmatoarele componente: cod
postal, localitate, strada, numar, nr. apartament. Intr-un SI realizat pentru activitatea unei administratii
financiare se impune descompunerea atributului adresa pe componentele sale elementare deoarece
contribuabilii sunt adesea selectati dupa criteriul strazii de domiciliu sau numarului, dar in cazul unui SI
destinat evidentei angajatilor unei firme atributul adresa se va retine ca atare, nefiind necesara
descompunerea sa pe elemente.

Regula minimizarii  identificatorilor specifica necesitatea stabilirii cu atentie a identificatorilor entitatilor retinand in grupul de atribute un numar cat mai mic de elemente (atribute).

Regula valorii NULL. Deoarece exista definite in cadrul tipurilor de entitati atribute care nu prezinta realizari obligatorii la nivelul fiecarei entitati, rezulta ca MCD poate fi rafinat prin definirea unor subtipuri de entitati care sa cuprinda doar atributele specifice acelei submultimi de entitati. Atributele cu rol de identificator vor trebui sa primeasca obligatoriu realizari.

II-4.2) Reguli de normalizare a MCD

Normalizarea este considerata o parte importanta a procesului de proiectare a datelor. Modelul EA este rezultatul unui proces iterativ care a permis identificarea tipurilor de entitati, atributelor definite in cadrul acestora, a identificatorilor si a asocierilor. Normalizarea vizeaza atributele entitatilor pe care le analizeaza cu scopul eliminarii anomaliilor asigurandu-se astfel definirea unor tipuri de entitati 'libere' de dependente functionale tranzitive si multivaloare.

Procesul normalizarii se poate desfasura urmand una din urmatoarele abordari:

Varianta 'top down' caracterizata prin urmarirea respectarii formelor normale la nivelul
entitatilor;

Varianta 'bottom up' caracterizata prin definirea unui tip de entitate unic ingloband toate
atributele modelului EA la nivelul caruia sa se identifice multimea dependentelor functionale
existente intre ele.

Regulile de normalizare a MCD sunt:

Regula nr. 1: Fiecare entitate trebuie sa prezinte un identificator prezentand realizari unice, nenule.

Aceasta regula este consecinta directa a definirii tipului de entitate in cadrul MCD. O regula suplimentara celei enuntate este cea referitoare la caracterul elementar al atributelor.

Regula nr. 2 Toate atributele entitatii, altele decat identificatorul, trebuie sa fie in dependenta functionala completa si directa cu identificatorul entitatii.

Altfel spus, in toate realizarile tipului de entitate, fiecare atribut trebuie sa fie determinat de identificator si trebuie sa ia o singura valoare si numai una (nu se admit valori multiple deci dependente functionale multivaloare). Sintagma de dependenta completa exprima necesitatea ca atributele sa fie determinate de identificator in ansamblul lui, si nu doar de o parte a lui (nu se admit dependente partiale).

Din cele mentionate rezulta faptul ca o entitate care prezinta identificatorul format dintr-un singur atribut respecta automat aceasta regula.

Regula nr. 3: Toate atributele unei asocieri trebuie sa depinda complet de identificatorul asocierii (format din identificatorii entitatilor participante la asociere) iar fiecare atribut trebuie sa depinda de intregul identificator al asocierii si nu de o parte a acestuia.

II-5 Dezvoltari ale modelului EA Generalizarea si specializarea.

II-5.1) Subtipuri si supertipuri de entitati

Un subtip (o subclasa) de entitati reprezinta un grup de entitati apartinand unui tip, reprezentate distinct in cadrul modelului, ele prezentand anumite trasaturi caracteristice ce le detaseaza, individualizeaza, de celelalte entitati.

Definirea subtipurilor de entitati se poate face pe doua cai:

plecand de la valoarea unui atribut (valorile unor atribute);

folosind anumite criterii precizate de utilizator (atribute specifice);

Prin aceasta grupare a entitatilor apartinand unui tip se ajunge la definirea unor supertipuri de entitati dominante in raport cu subtipurile (subclasele) acestora. Subclasele sunt rezultanta unei specializari la nivelul entitatilor, ele conservand insa capacitatea de a mosteni de la supertipul lor elementele comune definitorii.

Exemplu.       Pentru a clarifica importanta definirii in modelul EA a tipurilor si subtipurilor de entitati va propunem urmatorul exemplu:

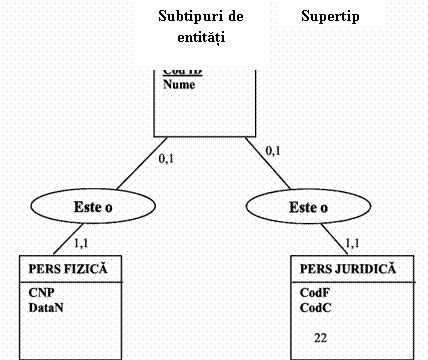
O banca lucreaza atat cu clienti persoane fizice cat si cu clienti persoane juridice. Fiecare client al bancii primeste un numar unic de identificare (cod ID), are un nume. Daca este persoana fizica se retine codul numeric personal (CNP) si data nasterii (DataN), daca este persoana juridica se retine codul fiscal (CodF) si codul din registrul comertului (CodC).

Fig.39)   Subtipuri de entitati

Cele doua subtipuri - pers fizica si pers juridica - mostenesc toate caracteristicile definite pentru supertip (CLIENTI) si anume Cod ID si Nume

II-5.2) Generalizarea

Generalizarea reprezinta un proces de modelare a carui finalitate este reprezentata de definirea unui supertip regrupand toate atributele comune si a mai multor subtipuri regrupand atributele specifice unui subansamblu de realizari ale unui tip generic de entitati.

Conceptul de generalizare provine de la reprezentarea cunostintelor sub forma de retele semantice si se materializeaza printr-un predicat de forma 'este un' (mai este numita si relatie IS-A dupa forma engleza a predicatului).

Exemplu.      

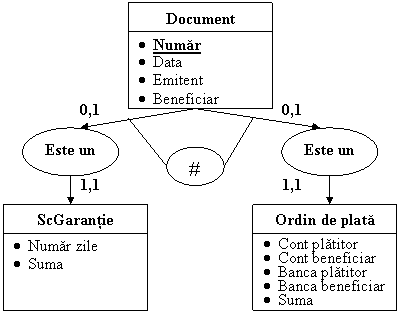
Sa luam un exemplu: orice document se identifica prin numar, data emiterii, emitent, beneficiar dar fiecare tip de document consemneaza un eveniment cu o anumita natura si continut. Astfel o scrisoare de garantie bancara indica perioada de valabilitate pentru care se garanteaza plata pentru o suma precizata. Un ordin de plata va aduce ca informatie specifica: numarul contului platitor, banca platitoare, contul beneficiar, banca acestuia, suma platita. Se pot reprezenta astfel in mod distinct proprietatile comune ale tuturor documentelor (elementelor de identificare) de cele specifice (Figura

Fig.40)   Generalizarea in modelul EA

Generalizarea permite in cadrul modelului EA tocmai definirea acestor caracteristici comune in cadrul unui supertip de entitate urmand ca elementele specifice sa ramana a fi descrise la nivelul subtipurilor de entitati.

Pentru ca orice scrisoare de garantie bancara sau ordin de plata se definesc prin numar, data, emitent, beneficiar rezulta ca subtipurile de entitati ScGarantie si OrdinPlata vor mosteni atributele susmentionate de la supertipul DOCUMENT.

Generalizarea prezinta o serie de proprietati, partial comentate deja:

Mostenirea atributelor semnificand faptul ca orice entitate e1 (ScGarantie/OrdinPlata) avand cu o alta entitate E (DOCUMENT) o relatie de generalizare, de forma E1 este un E, mosteneste atributele lui E;

Atributele supertipului nu apartin subtipului;

Nu exista mostenire colaterala (intre ScGarantie si OrdinPlata)

Figura 2.40. cuprinde si precizarea restrictiei de integritate de excluziune (o scrisoare de garantie nu poate fi un ordin de plata).

II-5.3) Specializarea

Specializarea reprezinta operatia opusa generalizarii permitand realizarea unei decupari a unui tip de entitate E (care va deveni SUPERTIP) in subtipuri de entitati diferentiate prin atribute proprii sau prin anumite realizari apartinand unui atribut.

Specializarea si generalizarea sunt doua abordari diferite ale aceluiasi proces de modelare.

In masura in care dorim sa cuprindem in modelul EA informatia existenta in documentele Scrisoare de garantie bancara si Ordin de plata (emis de agentul economic) putem crea initial un tip de entitate document definit prin multimea atributelor corespunzatoare problemei analizate (multimea tuturor atributelor celor doua tipuri de documente).

Tipul de entitate DOCUMENT (Figura 2.41) este un concept generic, el cuprinzand elementele caracteristice celor doua documente apartinand lumii reale, Scrisoarea de garantie si Ordinul de plata. Chiar daca pot exista atribute cu realizari optionale in cadrul unui tip de entitate, totusi daca acestea privesc caracteristici particulare ale unor entitati este necesara 'gruparea' acestora in subtipuri (de entitati). La nivelul tipului de entitate (Document) vor ramane doar atributele comune subtipurilor definite. Obtinem astfel subtipurile de entitati ScGarantie si OrdinPlata ajungand astfel la modelul EA prezentat in figura

Fig.41)  

Operatia de specializare poate fi: totala sau partiala.

Specializarea totala corespunde situatiei in care orice entitate a supertipului face parte dintr-un subtip. Grafic se marcheaza printr-o linie dubla.

Specializarea partiala corespunde situatiei in care pot exista realizari ale supertipului care nu apartin nici unui subtip (spre exemplu o realizare a tipului document este un document de tip bon de consum caruia nu-i corespunde nici un subtip din cele definite - in exemplul nostru ScGarantie si OrdinPlata). Grafic aceasta se reprezinta printr-o linie simpla.

Exemplu.       Sa presupunem ca secretariatul unei facultati doreste sa evidentieze cele trei categorii de studenti pe care ii gestioneaza: studentii de la forma de invatamant zi, studentii cursurilor postuniversitare si studentii doctoranzi. Toti acesti studenti se definesc printr-o serie de atribute comune: numar matricol, nume, adresa, data nasterii care se retin la nivelul tipului de entitate STUDENT. Atributele specifice fiecarui grup de studenti apartinand unei anumite forme de pregatire se vor retine in subtipurile specifice. Astfel, studentii de la cursurile de zi se definesc prin: an (de studii), grupa, categorie (student inscris pe loc bugetat sau cu taxa), tip bursa. Studentii cursurilor postuniversitare se caracterizeaza prin: cursul urmat, tema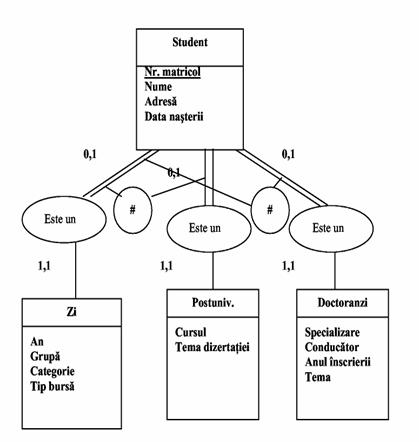 aleasa pentru dizertatie iar studentii doctoranzi se definesc prin: specializare, conducator stiintific, tema tezei, anul inscrierii.

Fig.42)       Specializare totala

Figura 2.42 evidentiaza faptul ca orice entitate apartinand tipului student isi gaseste corespondent intr-o realizare a unui subtip. S-a marcat distinct si de aceasta data restrictia de integritate de excluziune dintre subtipurile de entitati (daca este un student la zi nu poate fi student la un curs postuniversitar sau doctorand). Exista situatii in care intre cele doua subtipuri de entitati avand acelasi supertip pot aparea si restrictii de incluziune, deci realizarile cele doua subtipuri nu sunt disjuncte (figura 2.43).

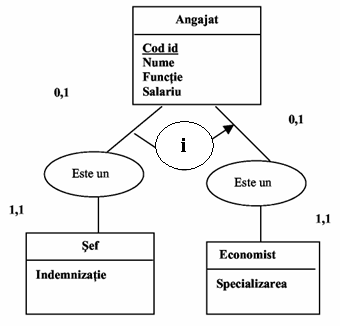
Seful unui compartament din structura organizatorica a firmei poate fi economist deci apare relatia de incluziune intre cele doua subtipuri definite - SEF si ECONOMIST

Fig.43)   Restrictie de integritate de incluziune

II-5.4) STUDIU DE CAZ

Se doreste realizarea modelului conceptual al datelor pentru sistemul informatic al unei societati de valori mobiliare stiind ca:

Ordinele de tranzactionare se primesc de la clienti, fiecare client fiind definit printr-un cod unic
de identificare, nume, adresa, banca, cont.

Ordinele de tranzactionare vizeaza societatile cotate pe piata, societati pentru care se retine
codul, denumirea, capitalul social, cotatia maxima si respectiv cotatia minima inregistrata.

Ordinele clientilor privesc o anume societate tranzactionata si pot fi de vanzare, (caz in care
acesta poate specifica pretul minim pe care il accepta) sau de cumparare, pentru care poate
preciza un pret maxim. Ordinele primesc un numar unic la nivelul SVM-ului si cuprind: data si
ora emiterii, numarul de actiuni, societatea vizata.

Ordinele sunt executate de un broker, clientii lucrand fiecare cu un anume broker din societate,
pentru care se retin urmatoarele caracteristici: cod si nume.

Tranzactiile realizate pe baza ordinelor primite prezinta: un numar, data tranzactiei, numarul
actiunilor care au facut obiectul tranzactiei, pretul la care s-a realizat tranzactionarea.

Un ordin poate fi acoperit prin mai multe tranzactii realizate pe piata.

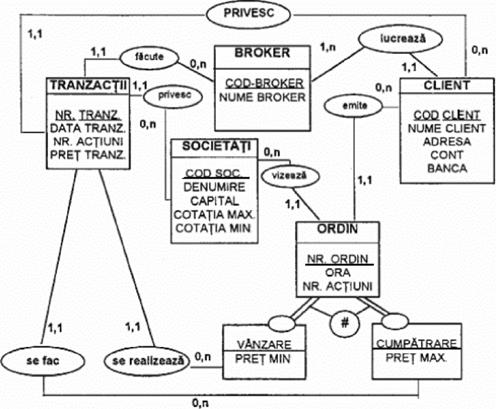
Fig.44)  

In MCD s-au definit urmatoarele tipuri de entitati:

Client definit prin atributele: Cod-client (identificator), nume-client, adresa, cont, banca.

Societati definit prin: Cod soc (identificator), denumire, capital, cotatia maxima, cotatia minima (aceste doua ultime atribute au rol informativ iar prin cerintele problemei nu s-a cerut si retinerea datelor la care s-au inregistrat aceste valori).

Ordin definit prin: Nr-ordin (identificator), data ordin, ora, nr-actiuni. Se remarca in cadrul MCD specializarea totala (cu specificarea restrictiei de excluziune intre entitatile subtipurilor) prin definirea subtipurilor Vanzare si Cumparare necesare retinerii pretului minim de vanzare respectiv pretului maxim de cumparare.

Tranzactii: Nr-tranz (identificator), data tranz, nr. actiuni, prettranz.

Broker: Cod-broker (identificator), nume broker.

II-6 Reprezentarea timpului

Modulul EA nu ofera formalisme specializate pentru reprezentarea timpului. Dar elementul timp trebuie de cele mai multe ori sa se regaseasca in cadrul modelului conceptual definit. Asa se explica faptul ca modelul EA permite atat reprezentari sincronice (care aduc o viziune atemporala) sau diacronice (care surprind elementul timp in MCD).

Sa presupunem ca dorim sa realizam un MCD care sa permita reprezentarea consumului specific de materii prime necesare fabricarii fiecarui subansamblu din componenta unui produs finit (Figura 2.45). Modelul conceptual din figura 2.45 este o reprezentare sincronica. Realitatea modelata nu a impus integrarea in MCD a elementului timp.

Sunt insa situatii in care in cadrul MCD este necesar sa integram si elementul timp. Sa presupunem ca dorim sa reprezentam cursele realizate de fiecare aeronava a unei companii de transporturi aeriene. Ne intereseaza sa cunoastem ce aeronava a asigurat fiecare din cursele programate. Vor fi utilizate in cadrul modelului doua tipuri de entitati AVION si CURSA intre cele doua stabilindu-se tipul de asociere REALIZEAZA.

Fig.45)  

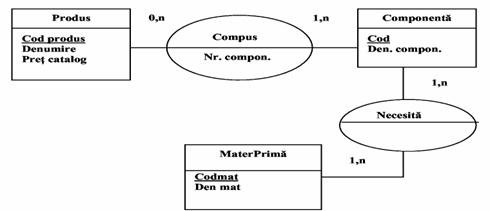
Reprezentare sincronica a consumului specific de materii prime

Fig.46)  

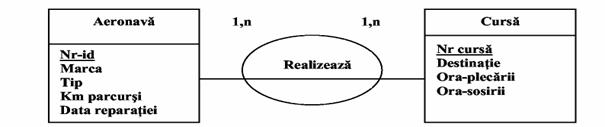
Reprezentare sincronica cursele programate ale aeronavelor

v            Realizarea reprezentarii diacronice prin introducerea unui tip de entitate temporala.

Reprezentarea sincronica din figura 2.46 evidentiaza ce curse au fost realizate de fiecare aeronava din dotare dar nu si cand. Cursa cu numarul 123 avand destinatia Paris se efectueaza in fiecare zi de joi a saptamanii si deci nu putem identifica cu ce aeronava s-a realizat intr-o numita zi. Daca insa dorim sa avem o evidenta clara a curselor realizate de o anumita aeronava aceasta reprezentare se dovedeste neacoperitoare. Realizarile tipului de asociere se identifica dupa Nr-ID si Nr cursa. Cum acelasi avion poate realiza aceeasi cursa, de mai multe ori identificarea realizarilor tipului de asociere nu se mai poate realiza. Acest lucru impune introducerea in cadrul modelului a unui tip de entitate temporala.

Caracteristic pentru entitatile temporale este faptul ca ele sunt definite adesea printr-un singur atribut (data calendaristica). In cazul in care prezinta mai multe atribute, fiecare dintre acestea reprezinta o unitate de masura a timpului (zi, ora, minut) iar ansamblul acestor atribute formeaza identificatorul tipului de entitate.

Observam ca introducerea timpului de entitate temporala a condus la transformatea tipului de asociere binara existent initial intre AVION si CURSA intr-o asociere ternara.

Fig.47)  

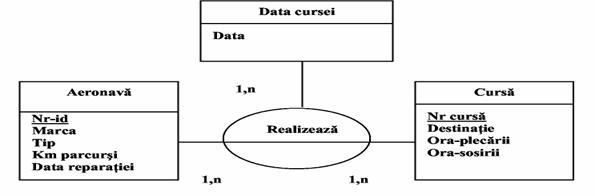
Reprezentare diacronica cursele programate ale aeronavelor

v            Realizarea reprezentarii diacronice prin introducerea evenimentelor datate

O alta modalitate de a introduce elementul timp in cadrul modelului EA este reprezentata de introducerea evenimentelor datate. Din activitatea practica cunoastem faptul ca fiecare eveniment produs (o aprovizionare, incheierea unui contract, etc.) se concretizeaza intr-un document care pe langa numar si prezentarea continutului prezinta si o data.

Sa luam cazul unei societati de asigurari si sa ne limitam la gestiunea doar a politelor de asigurare a bunurilor. In cadrul MCD trebuie sa cuprindem atat clientii societatii, bunurile pe care acestia le asigura si riscurile pentru care se face asigurarea.

Evenimetul bun asigurare care are loc se consemneaza intr-un document numit polita de asigurare. Acest eveniment se va regasi in cadrul MCD sub forma unui tip de entitate (Polita).

Fig.48)   Introducerea evenimentelor datate in modelul EA

II-7 Validarea modelelor externe

Validarea MCD nu se realizeaza doar prin regulile de validare si normalizare (prezentate intr-un
capitol anterior) vizand elemente de 'constructie' ale modelului ci si prin controlul completitudinii
modelului. Trecerea la etapa modelarii logice nu se poate face fara verificarea completitudinii modelului
conceptual.

MCD este definit prin prisma unei structuri semantice a datelor. Dar in realitate diferiti utilizatori prelucreaza datele conform nevoilor lor, avand din aceasta cauza o perceptie diferita (modele externe) asupra datelor.

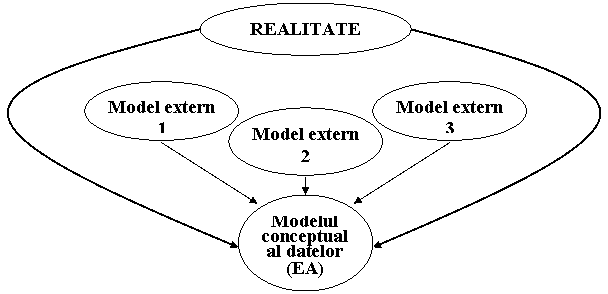
Fiecarei prelucrari (consultare sau actualizare) realizate de un utilizator ii corespunde un model extern al datelor (MED) care reflecta viziunea particulara a utilizatorului asupra realitatii. Acest model extern propriu unei anumite prelucrari implica un bloc logic de date constituit pe baza formalismului modelului EA.

Fig.49)   Modele externe ale datelor

Daca in urma definirii modelelor externe constatam ca fiecare dintre acestea este deductibil din MCD definit, inseamna ca modelul conceptual al datelor raspunde criteriului de completitudine.

In construirea modelelor externe se recomanda utilizarea urmatoarelor reguli:

se defineste un model extern pentru fiecare consultare sau actualizare impusa de o prelucrare;

modelul extern se construieste utilizand formalismul modelului EA.

In construirea modelului EA corespunzator MED se tine seama de faptul ca:

entitatile MED pot sa nu prezinte identificatori;

atributele, entitatile si asocierile MED pot sa nu-si gaseasca un corespondent in MCD;

atributele MED corespunzatoare celor apartinand MCD vor trebui sa aibe acelasi nume.

In cazul unei actualizari sau consultari, construirea MED va trebui sa redea si fluxul de date implicat in cadrul prelucrarii.

Astfel, in cazul operatiei de actualizare privind facturile emise clientilor, MED se prezinta astfel:

Fig.50)   MED al operatiei de actualizare

Din analiza MED prezentat in figura 2.50 constatam ca unele atribute isi gasesc corespondent direct in MCD, altele sunt atribute calculate (VAL-PRODUS, TVA-PRODUS, TOTAL-PRODUS) iar unele atribute, desi definesc aceleasi caracteristici, sunt definite cu nume diferite de cele utilizate in MCD (Client in loc de DEN CLIENT de exemplu), deci prin echivalenta isi gasesc un corespondent in MCD.

Atributele calculate apartinand MED vor fi descompuse in conformitate cu algoritmii de calcul utilizati in vederea identificarii operanzilor.

Se verifica apoi masura in care atributele se regasesc direct sau prin echivalenta in MCD.

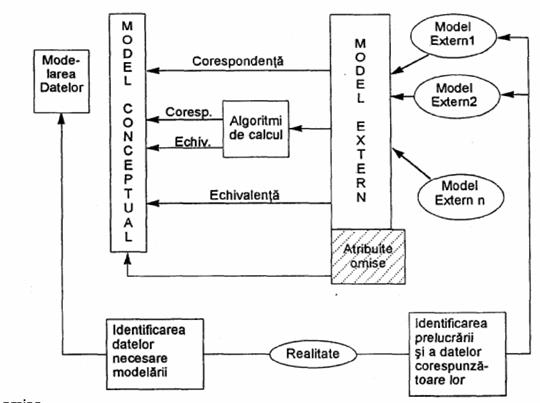
In masura in care MED cuprinde si atribute care nu se regasesc in MCD este necesara completarea acestuia cu atributele omise.

Fig.51)   Verificarea completitudinii MCD

v            Reguli de validare a modelelor externe

Ø      La prelucrarea - CONSULTARE

1) Atributele din modelele externe trebuie sa fie atribute din modelul conceptual.

2) Se verifica existenta in MCD a atributelor necesare identificarii datelor in procesul consultarii.

3) Cardinalitatile asocierilor din modelele externe trebuie sa fie incluse in cardinalitatile asocierilor apartinand MCD corespunzatoare semantic.

Ø     La prelucrarea - ACTUALIZARE

Orice atribut din modelul extern serveste fie la identificarea unui element de actualizare (atribut, entitate) din modelul conceptual, fie la obtinerea valorii de actualizare a unui element din modelul conceptual. Aceasta regula permite identificarea atributelor omise ce vor completa MCD precum si la identificarea atributelor MED care vor fi sterse deoarece nu servesc niciunuia din scopurile amintite.

Cardinalitatile asocierilor din modelele externe trebuie sa se includa in cardinalitatile asocierilor din modelelul conceptual, corespunzatoare semantic.

Orice element din modelul conceptual trebuie sa poata fi actualizat (adaugat, modificat, sters) prin cel putin unul din modele externe. In acest sens se vor defini modelele externe omise care realizeaza actualizarea tuturor elementelor conceptuale.