| CATEGORII DOCUMENTE |
| Animale | Arta cultura | Divertisment | Film | Jurnalism | Muzica |
| Pescuit | Pictura | Versuri |
Formalizarea logica a unui sistem este o reprezentare logica, in raport cu functia programata a sistemului, cu ajutorul starilor prin care evolueaza componenta sau a unor evenimente asociate acestora.
Deoarece formalizarea logica se raporteaza la functia programata a sistemului, este necesara analiza la nivel de sistem, a notiunilor de functie programata si nivel de succes.
In cazul sistemelor mono-componenta starea de succes coincide cu realizarea functiei programate, deci succesul componentei coincide cu succesul sistemului.
In cazul sistemelor pluri-componente, deoarece componentele din structura au contributii diferite la functia programata, prin defectare rezulta stari care nu sunt nici de succes total si nici de refuz total. Altfel spus, sistemul nu evolueaza numai prin doua stari de tipul "se realizeaza functia programata" si "nu se realizeaza functia programata", astfel aparand situatii intermediare care pot fi definite cu ajutorul notiunii de nivel de succes al sistemului.
Cele mai folosite formalisme de logice bazate sunt cele:
bazate pe stari:
o tabele de adevar;
o diagrame de succes;
o ansambluri minimale;
o functii de structura;
o grafuri ale tranzitiilor intre stari;
bazate pe evenimente:
o arbori de defectare;
o arbori de evenimente.
Diagrama de fiabilitate (DF) este o reprezentare logica a sistemului in raport cu starea de succes (functia programata), sub forma unui graf in care nodurile sunt starile de succes (functionare) ale componentelor, iar arcele legaturile logice dintre acestea. Succesul sistemului (realizarea functiei programate) este dat de exista a cel putin unei cai intre intrarea si iesirea din graf. Se obisnuieste ca nodurile sa fie simbolizate prin dreptunghiuri si arcele prin drepte.
Diagrama de fiabilitate este cea mai apropiata reprezentare a unui formalism logic de schema tehnologica reala insa cele doua nu trebuie a fi confundate. Pentru nivele de succes diferite ale aceluiasi sistem rezulta diagrame de fiabilitate diferite.
Pentru acest tip de formalizare logica se recomanda parcurgerea urmatoarelor etape:
Stabilirea schemei tehnologice reale si identificarea componentelor si a contributiei lor la functia programata;
Reducerea evolutiei componentelor la doua stari: functionare, respectiv, avarie;
Precizarea nivelului de succes in raport cu care se construieste diagrama de fiabilitate;
Construirea diagramei de fiabilitate;
Evaluarea diagramei de fiabilitate (determinarea probabilitatilor de realizare a functiei programate).
Diagramele de fiabilitate pot fi clasificate in doua mari categorii:
Diagrame de fiabilitate simple (DFS);
Diagrame de fiabilitate complexe (DFC).
Diagramele de fiabilitate simple sunt cele care se pot descompune numai in diagrame elementare de tip serie si paralel.
DF de tip serie;
DF de tip paralel;
DF de tip "k din n";
DF de tip serie-paralel;
DF de tip paralel-serie.
Diagramele de fiabilitate complexe sunt cele care nu se pot descompune numai cu ajutorul diagramelor simple, necesitand tehnici speciale de evaluare logica.
Fie un sistem S format din N componente. Fiecare componenta are asociata o variabila booleana de top 0 / 1 (adevarat / fals):
![]() ( . )
( . )
si fie ![]() ,
vectorul de stare al sistemului S. Functia de structura este definita prin:
,
vectorul de stare al sistemului S. Functia de structura este definita prin:
![]() ( . )
( . )
Functia de structura reprezinta un formalism logic algebric boolean care se bazeaza pe punerea in corespondenta a campului de evenimente ce defineste comportarea aleatoare a sistemului, cu un spatiu boolean al starilor sistemului de forma N. Intre operatorii logici ai campului si operatorii spatiului boolean exista urmatoarea corespondenta:
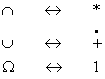
Æ 0 ( . )
Proprietatile spatiului, in corespondenta cu cele ale campului de evenimente, sunt prezentate in Tabelul . .
Fie![]() ,
,
![]() .
Se numeste variabila esentiala xi variabila pentru care
.
Se numeste variabila esentiala xi variabila pentru care ![]() .
.
Doua functii sunt egale daca ele se deduc una din alta prin adaugarea de variabile neesentiale.
Functia duala a unei functii de structura rezulta din:
![]() ( . )
( . )
Functia de structura este monotona in raport cu variabila xi daca:
![]() ( . )
( . )
Daca ![]() este monotona in raport cu toate variabilele
ei, atunci ea este monotona. O functie de structura este coerenta daca este
monotona si daca:
este monotona in raport cu toate variabilele
ei, atunci ea este monotona. O functie de structura este coerenta daca este
monotona si daca:
![]() ( . )
( . )
Tabelul . Corespondenta operatiilor intre campul de evenimente si spatiul boolean
|
Campul de evenimente |
Spatiul boolean |
|
1. Comutativitatea |
|
|
A B=B A |
x*y = y*x |
|
AÈB=BÈA |
x |
|
2. Asociativitatea |
|
|
A (B C)=(A B) C |
x*(y*z) = (x*y)*z |
|
AÈ(BÈC)=(AÈB) ÈC |
x |
|
3. Distributivitatea |
|
|
A (BÈC)=(A B) È(A C) |
x*(y |
|
AÈ(B C)=(AÈB) (AÈC) |
x |
|
4. Idempotenta |
|
|
A A=A |
x*x = x |
|
AÈA=A |
x |
|
5. Absorptia |
|
|
A (AÈB) = A |
x*(x |
|
AÈ(A B) = A |
x |
|
6. Teoreme de baza |
|
|
|
|
|
|
|
Un sistem, are in raport cu functia lui programata o diagrama echivalenta de tip serie, daca starea de succes a sistemului presupune functionarea simultana a tuturor componentelor sale (toate componentele sale se afla in stare de functionare)
![]()
Figura . Diagrama de fiabilitate de tip serie
Daca se defineste functionarea sistemului cu ajutorul logicii combinarice ale starilor de functionare pentru componentele sale, expresia logica a realizarii functiei programate rezulta din urmatorul rationament: sistemul se afla in stare de succes daca componenta 1 se afla in stare de succes si componenta 2 se afla in stare de succes si componenta N se afla in stare de succes.
![]()
![]() ( . )
( . )
, unde S si R reprezinta starile de
functionare (succes) si nefunctionare (refuz) ale sistemului, iar , i si ![]() starile
de functionare si nefunctionare ale unei componente i a sistemului.
starile
de functionare si nefunctionare ale unei componente i a sistemului.
Probabilitatea ca sistemul sa se afle in stare de succes rezulta din evaluarea expresiei logice anterioare, apeland la regulile de evaluare a expresiilor logice. In cazul general, cand evenimentele nu sunt mutual exclusive se aplica teorema probabilitatilor conditionate:
![]() (1.2)
(1.2)
In cazul in care ipoteza starile sunt mutual exclusive rezulta relatia:
![]() (1.2)
(1.2)
, unde ![]() este probabilitatea de succes a componentei i.
este probabilitatea de succes a componentei i.
Din relatia de mai sus se remarca probabilitatea mai mica de succes a sistemului decat cea mai nefiabila componenta a sa.
In Tabelul . sunt prezentati principalii indicatori de fiabilitate si disponibilitate in cazul functiilor de repartitie exponentiale pentru sistemele descrise de diagramele de fiabilitate de tip serie.
Tabelul . Relatii de calcul a indicatorilor sistemelor serie pentru componente cu functii exponentiale de repartitie
|
Indicator de fiabilitate |
Relatie de calcul |
|
Functia de fiabilitate |
|
|
Functia nonfiabilitate (functia de repartitie) |
|
|
Media timpului de functionare neintrerupta |
|
|
Intensitatea echivalenta de avarie |
|
|
Disponibilitatea nestationara |
|
|
Disponibilitatea stationara |
|
Diagramei de fiabilitate de tip serie ii corespunde functia de structura:
![]() (1.2)
(1.2)
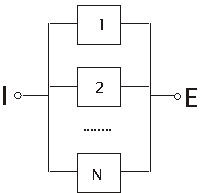
Un sistem are, in raport cu functia lui programata, o diagrama de
fiabilitate de tip paralel, daca starea sa de functionare se obtine prin
functionarea oricarei dintre componentele sale. Starea de avarie pentru un
astfel de sistem se obtine cand toate componentele sale sunt in stare de
avarie. In Figura . este reprezentat grafic un astfel de sistem.
Figura . Diagrama de fiabilitate de tip paralel
Sistemul se afla in stare de succes daca componenta 1 se afla in stare de succes sau componenta 2 se afla in stare de succes sau sau componenta N se afla in stare de succes.
![]()
![]() (1.2)
(1.2)
Pentru calculul unor astfel de sisteme se apeleaza la teorema Sylvester-Poincare:
 (1.2)
(1.2)
Pentru cazul componentelor independente se poate scrie:
![]() (1.2)
(1.2)
, unde ![]() este probabilitatea de refuz a componentei i.
(
este probabilitatea de refuz a componentei i.
(![]() )
)
O alta forma de calcul a probabilitatii de succes a sistemului este:
![]() (1.2)
(1.2)
In Tabelul . sunt prezentate formulele pentru calculul indicatorilor de fiabilitate pentru sistemele paralel, in cazul sistemelor cu componente avand functii de repartitie exponentiale.
Tabelul . Indicatorii de fiabilitate ai sistemelor paralel cu componente avand functii de repartitie exponentiale.
|
Indicator de fiabilitate |
Relatie de calcul |
|
Functia de fiabilitate |
|
|
Functia de nonfiabilitate |
|
|
Media timpului de functionare neintrerupta |
|
|
Intensitatea echivalenta de avarie |
|
|
Disponibilitatea nestationara |
|
|
Disponibilitatea stationara |
|
Diagramei de fiabilitate de tip paralel ii corespunde functia de structura:
![]()
(1.2)
O diagrama de fiabilitate generalizata este cea de tip k din N la care starea de functionare a sistemului presupune functionarea simultana a cel putin k componente din cele N ale sistemului (Figura . ). Se poate observa ca:
daca k=N se obtine diagrama de tip serie;
daca k=1 se obtine diagrama de tip paralel.
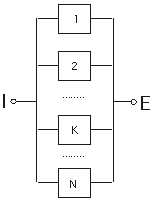
Figura . Diagrama de fiabilitate de tip k/N
Pentru calculul acestor tipuri de sisteme se
poate porni de la urmatoarea propozitie logica: sistemul se afla in stare de
succes daca k componente se afla in
stare de succes sau k+1 componente se
afla in stare de succes sau sau N
componente se afla in stare de succes. Daca se alege ca variabila aleatoare K,
numarul de componente simultan in stare de succes, sau numarul ![]() de componente in stare de refuz, rezulta:
de componente in stare de refuz, rezulta:
![]()
![]() (1. )
(1. )
Daca pentru un astfel de model componentele sunt independente, se poate apela la modelul binomial:
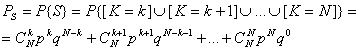 (1. )
(1. )
, unde ![]()
Reprezinta o serie de submodule, fiecare reprezentand o diagrama de fiabilitate de tip paralel (Figura 1.4).
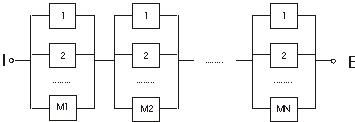
Figura . Diagrama de fiabilitate de tip serie-paralel
In Figura 1.4, N este numarul de module in serie, iar M este numarul de componente in paralel ale submodulului. Probabilitatea de succes a sistemului este:
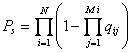 (1. )
(1. )
,unde ![]() este probabilitatea de refuz a componentei din
submodulul i cu numarul de ordine j.
este probabilitatea de refuz a componentei din
submodulul i cu numarul de ordine j.
Diagramei de fiabilitate de tip serie-paralel ii corespunde functia de structura:
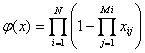 (1. )
(1. )
Reprezinta o diagrama de tip paralel in care elementele paralelului sunt diagrame de fiabilitate de tip serie (Figura . ).
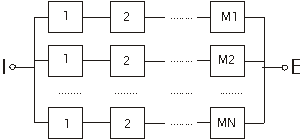
Figura . Diagrama de fiabilitate de tip paralel- serie
Calculul probabilitatii de functionare a unui astfel de sistem se poate face cu ajutorul formulei de mai jos:
 (1. )
(1. )
,unde N este numarul de submodule ale paralelului, iar M numarul de
componente ale submodulului, ![]() fiind probabilitatile de functionare ale unei
componente j din submodulul i.
fiind probabilitatile de functionare ale unei
componente j din submodulul i.
Diagramei de fiabilitate de tip paralel-serie ii corespunde urmatoarea functie de structura:
 (1. )
(1. )
Evaluarea unei diagrame de fiabilitate complexe nu poate fi facuta direct, utilizandu-se diagrame de fiabilitate de tip serie si paralel, ci doar utilizand tehnici de descompunere.
Sistemul se afla in stare de succes daca sistemul functioneaza cu componenta i in functiune sau sistemul functioneaza cu componenta i in avarie.
![]() (1. )
(1. )
Probabilitatea de succes a sistemului reprezentat printr-o diagrama de fiabilitate complexa se determina:
![]() (1. )
(1. )
Se alege componenta i astfel incat diagramele obtinute prin conditionarea ca componenta i sa fie in stare de functionare sau in stare de avarie sa conduca la diagrame de fiabilitate simple.
In continuare vor fi prezentate, pentru exemplificare, doua cazuri calcul a diagramelor de fiabilitate complexe (Figura . ).
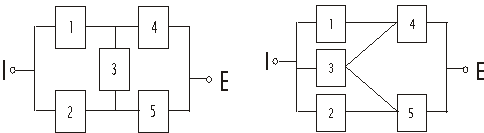

Cazul 1 Cazul 2
Figura . Diagrama de fiabilitate complexe
In ambele cazuri, componenta ce trebuie eliminata este 3 si rezulta:
![]() (1. )
(1. )
Pentru exemplele de fata, diagramele de fiabilitate se descompun dupa cum urmeaza:
Cazul 1:

serie-paralel paralel-serie
![]() sau
sau ![]()
![]() sau
sau ![]()
Figura . Calculul diagramelor de fiabilitate complexe (cazul 1)
Pentru a determina probabilitatea de succes a sistemului se considera qi - probabilitatea de insucces a componentei i, iar pi - probabilitatea de succes a componentei i, cu conditia pi = 1 - qi:
![]() ;
;![]()
![]() (1. )
(1. )
Pentru determinarea fiabilitatii sistemului se inlocuieste pi cu Ri(t) si qi cu Fi(t) (sau 1- Ri(t)).
Evaluarea diagramelor complexe cu ajutorul functiei de structura:
Luand in considerare afirmatiile de mai sus se obtine:
![]() ( . )
( . )
Daca componenta i este 3, atunci:
![]() ( . )
( . )
Se pot explicita functiile de structura ![]() si
si
![]() le corespunzatoare:
le corespunzatoare:
![]() ;
;![]()
![]() ( . )
( . )
Cazul 2:
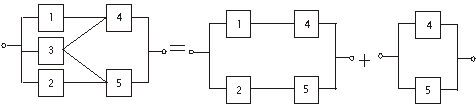
paralel-serie paralel
![]() sau
sau ![]()
![]() sau
sau ![]()
Figura . Calculul diagramelor de fiabilitate complexe (cazul 2)
![]() ;
;
![]() ;
;
![]() ( . )
( . )
Functia de structura:
![]() ;
;
![]() ;
;
![]() . ( . )
. ( . )
Vectorul ![]() este critic pentru componenta i daca
este critic pentru componenta i daca ![]() si
si ![]() .
.
Factorul de importanta structurala Birnbaum, ![]() ,
este exprimat prin numarul de vectori critici ai componentei "i", raportat la numarul total de vectori
(stari ale sistemului) care pot exista in calculul factorului de importanta.
,
este exprimat prin numarul de vectori critici ai componentei "i", raportat la numarul total de vectori
(stari ale sistemului) care pot exista in calculul factorului de importanta.
![]() ( . )
( . )
, unde n este numarul de componente ale sistemului.
Factorul de importanta structurala Barlow -
Prochan, ![]() ,
este exprimat prin probabilitatea medie de vectori critici pentru componenta "i":
,
este exprimat prin probabilitatea medie de vectori critici pentru componenta "i":
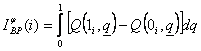 ( . )
( . )
, unde ![]() ,
iar Q este probabilitatea de insucces
a sistemului.
,
iar Q este probabilitatea de insucces
a sistemului.
Factorul de importanta probabilista Birnbaum,
![]() ,
reprezinta probabilitatea ca vectorul X(t)
sa fie critic pentru componenta "i"
la momentul de timp "t".
,
reprezinta probabilitatea ca vectorul X(t)
sa fie critic pentru componenta "i"
la momentul de timp "t".
![]() ( . )
( . )
Factorul de importanta probabilista Barlow -
Prochan, ![]() ,
exprima probabilitatea ca defectarea componentei "i" sa fi provocat defectarea sistemului.
,
exprima probabilitatea ca defectarea componentei "i" sa fi provocat defectarea sistemului.
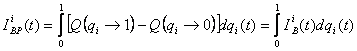 ( . )
( . )
Intensitatea de aparitie a starii de avarie a unei componente este:
![]() ( . )
( . )
, unde MUTi este timpul mediu de functionare al componentei "i", MDTi este timpul mediu de insucces al componentei "i", λi este intensitatea de defectare a componentei "i", μi este intensitatea de reparare a componentei "i".
Intensitatea de defectare a sistemului este:
![]() ( . )
( . )
, unde MUT este timpul mediu
de functionare al sistemului, MDT
este timpul mediu de insucces al sistemului, ![]() este
factorul de importanta probabilista Birnbaum al componentei "i", iar νi este intensitatea de aparitie a starii de defect
pentru componenta "i".
este
factorul de importanta probabilista Birnbaum al componentei "i", iar νi este intensitatea de aparitie a starii de defect
pentru componenta "i".
Timpul mediu de defectarea al sistemului se poate calcula cu ajutorul probabilitatii de insucces a sistemului Q:
![]() ( . )
( . )
Exemplu 1. Fie un sistem de tip paralel format din doua componente identice si independente 1 si 2. Se cunosc probabilitatile de insucces ale componentelor q si intensitatile lor de reparare μ. Care este timpul mediu de insucces pentru sistem:
Probabilitatea de insucces a sistemului este:
![]() ( . )
( . )
Factorii de importanta probabilista Birnbaum
pentru componente sunt ![]() ,
respectiv
,
respectiv ![]() .
.
Intensitatile de aparitie a starilor de
avarie sunt ![]() .
.
Intensitatea de aparitie a starii de defect a
sistemului este: ![]() .
.
Timpul mediu de insucces al sistemului este: ![]() .
.
Exemplu 2. Fie un sistem de tip serie format din doua componente identice si independente 1 si 2. Se cunosc probabilitatile de insucces ale componentelor q si intensitatile lor de reparare μ. Care este timpul mediu de insucces pentru sistem:
Probabilitatea de insucces a sistemului este:
![]() ( . )
( . )
Factorii de importanta probabilista Birnbaum
pentru componente sunt ![]() ,
respectiv
,
respectiv ![]() .
.
Intensitatile de aparitie a starilor de
avarie sunt ![]() .
.
Intensitatea de aparitie a starii de defect a
sistemului este: ![]() .
.
Timpul mediu de insucces al sistemului este: ![]() .
.
1) Fie un punct termic in care schema de curgere este cea din Figura . :
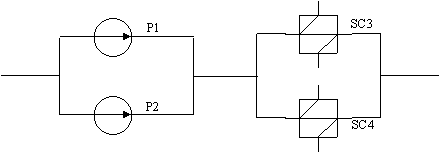

Figura . Schema tehnologica de incalzire si pompare a apei.
Atat pompele P1 si P2, cat si schimbatoarele de caldura SC3 si SC4 au distributii exponentiale ale timpilor de functionare, respectiv reparare. Intensitatile de defectare, reparare ale pompelor sunt lP=0,005 h-1, respectiv mP=0,012 h-1, in timp ce intensitatile de defectare, respectiv reparare ale schimbatoarelor de caldura sunt lSC=0,002 h-1, respectiv mSC=0,021 h-1. Sa se calculeze indicatorii de fiabilitate ai schemei in urmatoarele cazuri:
A. Debitul necesar a fi incalzit este de 200 t/h, in timp ce debitele nominale ale pompelor sunt de 100 t/h, iar cele ale schimbatoarelor de caldura sunt tot de 100 t/h.
B. Debitul necesar este de 100 t/h, iar debitele nominale ale pompelor sunt de 100 t/h, cele ale schimbatoarelor de caldura fiind de 100 t/h.
Rezolvare.
Componentele schemei vor fi notate dupa cum urmeaza:
Pompa 1 (P1) → 1;
Pompa 2 (P2) → 2;
Schimbatorul de caldura 1 (SC 1) → 3;
Schimbatorul de caldura 2 (SC 2) → 4.
Probabilitatile de functionare ale componentelor:
![]() ( . )
( . )
Functia de fiabilitate a componentelor:
![]() ( . )
( . )
Functia de disponibilitate a componentelor
![]() ( . )
( . )
Cazul A. Debitul necesar este de 200 t/h, in timp ce debitele pompelor si cele ale schimbatoarelor de caldura sunt de 100 t/h. Pentru acoperirea necesarului (functiei programate a sistemului) este necesara functionarea cu doua pompe (2 X 100 t/h = 200 t/h) si doua schimbatoare de caldura (2X 100 t/h).
Sistemul de pompare este de tip 2 X 50 %, pentru functionarea lui este nevoie de functionarea tuturor componentelor, ceea ce duce la un sistem serie in raport cu functia lui programata. In acelasi mod, sistemul de incalzire este de tip serie 2 X 50 % (de tip serie).
Diagrama de fiabilitate arata ca in Figura . :
![]()
![]()
Figura . Reprezentarea grafica a diagramei de tip serie.
Dat fiind faptul ca sistemul este unul de tip serie, probabilitatea de succes a lui este de tipul:
![]() ( . )
( . )
Fiabilitatea sistemului:
![]()
![]()
![]() ( . )
( . )
Cu ajutorul relatiei de mai sus s-a reprezentat grafic, in Figura . , functia de fiabilitate a sistemului.
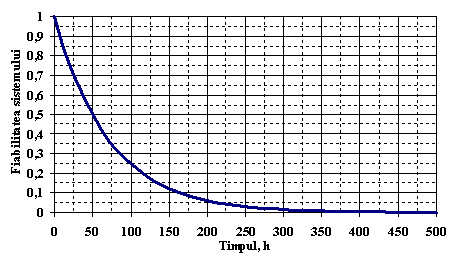
Figura . Reprezentarea grafica a functiei de fiabilitate a sistemului
Nonfiabilitatea sistemului:
![]() ( . )
( . )
Cu ajutorul relatiei de mai sus s-a reprezentat grafic, in Figura . , functia de nonfiabilitate a sistemului.
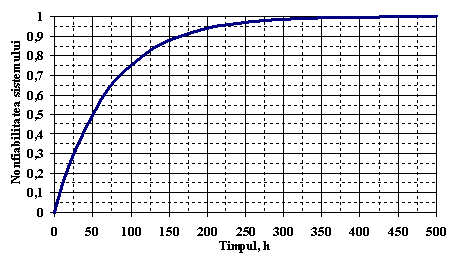
Figura . Reprezentarea grafica a functiei de nonfiabilitate a sistemului
Media timpului de functionare neintrerupta pana la prima avarie a sistemului este:
 ( . )
( . )
Intensitatea echivalenta de avarie este constanta:
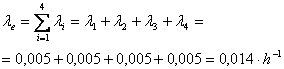 ( . )
( . )
Disponibilitatea sistemului:
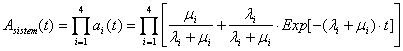
( . )
Figura . reprezinta disponibilitatea sistemului.
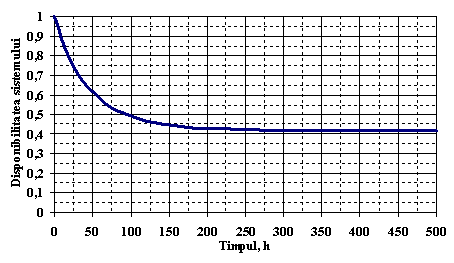
Figura . Reprezentarea grafica a functiei de disponibilitate a sistemului
Disponibilitatea stationara a sistemului (probabilitatea stationara de functionare a sistemului):
![]() ( . )
( . )
![]() ( . )
( . )
Cazul B. Debitul necesar este de 100 t/h, iar debitele pompelor si ale schimbatoarelor de caldura sunt de 100 t/h. Pentru acoperirea necesarului (functia programata a sistemului) este necesara functionarea cel putin unei pompe (una din doua) si a unui schimbator de caldura (din doua).
Sistemul de pompare este de tip 2 X 100 %, pentru functionarea lui este nevoie de functionarea unui singur component, aceasta ducand la un sistem paralel in raport cu functia lui programata. In acelasi mod, schimbatoarele de caldura functioneaza 2X100 % (in paralel).
Diagrama de fiabilitate a sistemului este de tipul serie - paralel, precum in Figura . :
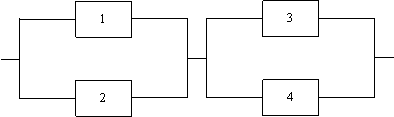

Figura . Reprezentarea grafica a diagramei de tip serie - paralel.
Dat fiind faptul ca sistemul este unul de tip serie, probabilitatea de succes a lui este de tipul:
![]()
![]()
( . )
In relatia de mai sus, pi reprezinta probabilitatea de succes a componentei "i".
Fiabilitatea sistemului:
![]()
![]()
![]() ( . )
( . )
Cu ajutorul relatiei de mai sus s-a reprezentat grafic, in Figura . , functia de fiabilitate a sistemului.
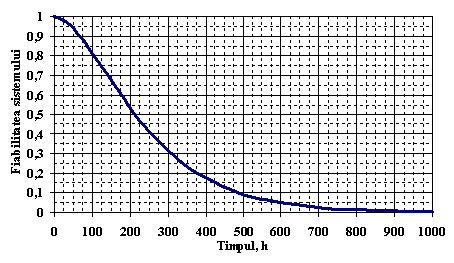
Figura . Reprezentarea grafica a functiei de fiabilitate a sistemului
Nonfiabilitatea sistemului:
![]() ( . )
( . )
Cu ajutorul relatiei de mai sus s-a reprezentat grafic, in Figura . , functia de nonfiabilitate a sistemului.
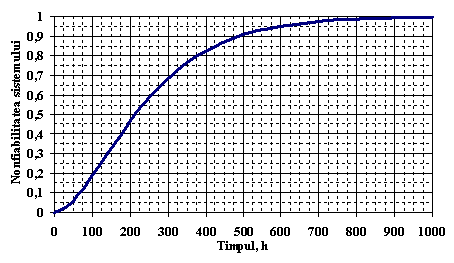
Figura . Reprezentarea grafica a functiei de nonfiabilitate a sistemului
Media timpului de functionare neintrerupta pana la prima avarie a sistemului:
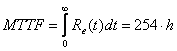 ( . )
( . )
Intensitatea echivalenta de avarie:
![]()
![]()
In Figura . este reprezentata grafic a intensitatii de avarie a sistemului:
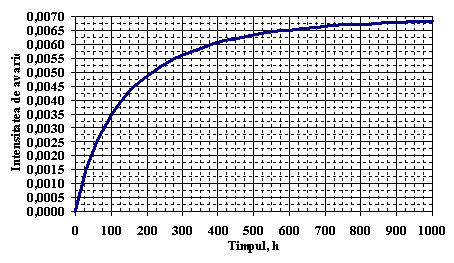
Figura . Reprezentarea grafica a intensitatii de avarie a sistemului
Disponibilitatea sistemului:
![]() ( . )
( . )
In relatia de mai sus ai(t) reprezinta disponibilitatea componentei "i" la momentul t. Figura . reprezinta disponibilitatea sistemului.

Figura . Reprezentarea grafica a functiei de disponibilitate a sistemului
Disponibilitatea stationara a sistemului (probabilitatea stationara de functionare a sistemului):
![]() ( . )
( . )
2) Fie o CET urbana echipata cu urmatoarele trei turbine:
Turbina 1, de tipul DSL 50, cu putere nominala de 50 MW, media timpilor de functionare de 3000 h si media timpilor de reparare de 240 h;
Turbina 2,de tipul DKUL 50, cu putere nominala de 50 MW, media timpilor de functionare de 3500 h si media timpilor de reparare de 240 h;
Turbina 3,tipul DKU 50, cu putere nominala de 50 MW, media timpilor de functionare de 3250 h si media timpilor de reparare de 240 h.
In ipoteza ca grupurile nu functioneaza la sarcini partiale si legile de repartitie ai timpilor de functionare, respectiv reparare sunt exponentiale sa se determine indicatorii de fiabilitate ai centralei pentru o cerere de putere de a) 50 MW, b) 100 MW si c) 150 MW.
Rezolvare. Intensitatile de avarie, respectiv reparare pentru echipamente sunt:
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]()
![]() .
.
Probabilitatile de functionare ale turbinelor sunt:
![]()
![]()
![]()
Functiile de fiabilitate ale turbinelor sunt:
![]()
![]()
![]()
Functiile de disponibilitate ale turbinelor sunt:
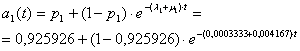
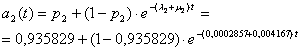
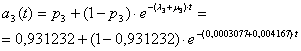
a) Daca puterea ceruta este de 50 MW, oricare dintre turbine poate acoperi aceasta sarcina, schema de fiabilitate fiind de tipul "paralel".
Probabilitatea de functionare a sistemului este:
![]()
Functia de fiabilitate a sistemului este:
![]()
In Figura . este reprezentata functia de fiabilitate a centralei.
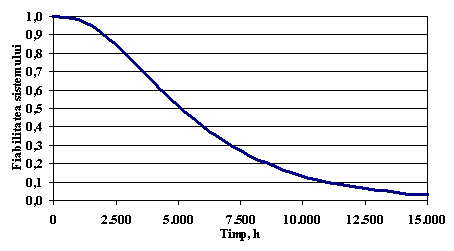
Figura . Reprezentarea grafica a functiei de fiabilitate a sistemului
Functia de disponibilitate a sistemului este:
![]() ( . )
( . )
In Figura . este reprezentata functia de disponibilitate a centralei.
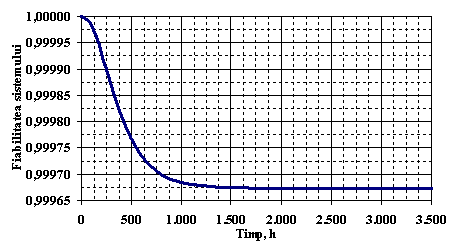
Figura . Reprezentarea grafica a functiei de disponibilitate a sistemului
Traseele minimale ale sistemului sunt , si ,
iar taietura minimala este ![]() .
.
Starile critice ale sistemului sunt: ![]() ,
,
![]() si
si ![]() .
.
Intensitatea de tranzitie din starea de functionare in starea de avarie este:
![]()
![]() ( . )
( . )
Timpul mediu de functionare este:
![]() ( . )
( . )
b) Daca puterea ceruta este de 100 MW, aceasta poate fi asigurata de functionarea simultana a oricaror doua turbine, diagrama de fiabilitate care modeleaza acest sistem este de tipul "doua din trei".
Probabilitatea de functionare a sistemului se poate modela cu ajutorul distributiei polinomiale:
![]() ( . )
( . )
Functia de fiabilitate a sistemului este:
![]() ( . )
( . )
In Figura . este reprezentata functia de fiabilitate a centralei.
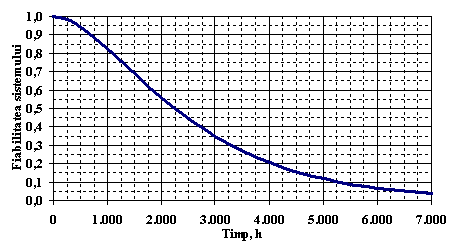
Figura . Reprezentarea grafica a functiei de fiabilitate a sistemului
Functia de disponibilitate a sistemului este:
![]() ( . )
( . )
In Figura . este reprezentata functia de disponibilitate a centralei.
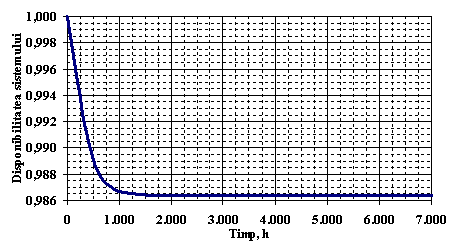
Figura . Reprezentarea grafica a functiei de disponibilitate a sistemului
Traseele minimale ale sistemului sunt
, si , in timp ce taieturile minimale ale sistemului sunt ![]() ,
,![]() si
si ![]() .
.
Starile critice ale sistemului sunt: ![]() ,
,
![]() si
si ![]() .
.
Intensitatea de tranzitie din starea de functionare in starea de avarie este:
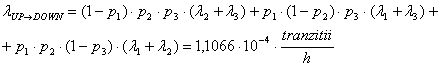
( . )
Timpul mediu de functionare este:
![]() ( . )
( . )
c) Daca puterea ceruta este de 150 MW, aceasta poate fi asigurata de functionarea simultana a tuturor turbinelor, diagrama de fiabilitate care modeleaza acest sistem este de tipul "serie".
Probabilitatea de functionare a sistemului este:
![]() ( . )
( . )
Functia de fiabilitate a sistemului este:
![]() ( . )
( . )
In Figura . este reprezentata functia de fiabilitate a centralei.
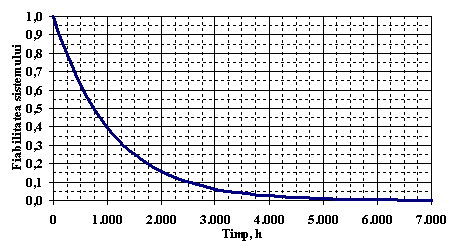
Figura . Reprezentarea grafica a functiei de fiabilitate a sistemului
Functia de disponibilitate a sistemului este:
![]() ( . )
( . )
In Figura 1.24 este reprezentata functia de disponibilitate a centralei.

Figura . Reprezentarea grafica a functiei de disponibilitate a sistemului
Traseul minimal al sistemului este ,
in timp ce taieturile minimale sunt ![]() ,
,![]() si
si ![]() .
.
Starea critica a sistemului este: ![]() .
.
Intensitatea de tranzitie din starea de functionare in starea de avarie este:
![]()
( . )
Timpul mediu de functionare este:
![]() ( . )
( . )
3) Fie un sistem format din noua componente independente si identice, cu intensitatea de defectare λ si intensitatea de reparare μ cunoscute. Diagrama de fiabilitate a sistemului este ce din Figura . .
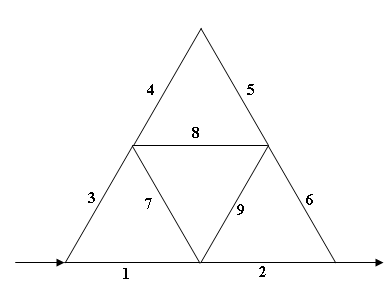
Figura . Diagrama de fiabilitate a sistemului.
Se cer:
a) traseele si taieturile minimale;
b) probabilitatea de functionare a sistemului;
c) timpul mediu de insucces al sistemului.
a) Traseele minimale ale sistemului sunt: T1 , T2 , T3 , T4 , T5 , T6 , T7 , T8 , T9 si T10.
Negandu-se reuniunea traseelor se obtine setul de taieturi: K1 , K2 , K3 , K4 , K5 , K6 , K7 si K8 .
b) Modeland setul de trasee minimale obtinute (cu ajutorul procedurii DNF prezentata in capitolul 1) se poate obtine functia de probabilitate de functionare a sistemului raportata la probabilitatea de functionare a componentelor:
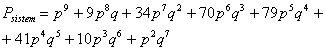 ( . )
( . )
O aproximare acoperitoare pentru calculul functiei este obtinuta prin calculul probabilitatii de succes a sistemului ca pentru un paralel format din cele 10 trasee:
![]() ( . )
( . )
Variatia grafica obtinuta prin calculul exact si cel aproximat al probabilitatii de succes a sistemului functie de probabilitatea de succes a componentelor este prezentata in Figura . .
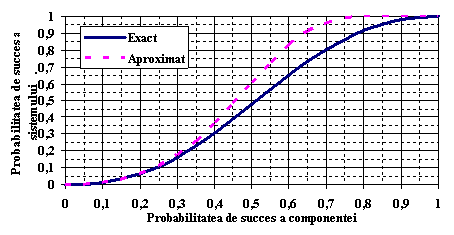
Figura . Variatia probabilitatii de succes a sistemului in functie de probabilitatea de succes a componentelor, calculate exact si aproximat.
c) Probabilitatea de insucces a sistemului este:
![]() ( . )
( . )
Calculand factorii de importanta probabilista Birnbaum pentru fiecare dintre componente vom obtine:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Intensitatea de avarie a sistemului este:
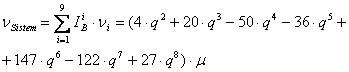 ( . )
( . )
, unde ![]()
Timpul mediu de insucces al sistemului este:
![]() ( . )
( . )
1) Fie un sistem format din 5 componente independente. Se cunosc:
Intensitatea de defectare λi (i = 1,2,3,4,5);
Probabilitatile de insucces qi (i = 1,2,3,4,5);
Taieturile minimale K1 , K2 , K3 , K4 .
Se cer: a) probabilitatile de succes pi (i = 1,2,3,4,5), b) traseele minimale ale sistemului, c) probabilitatea de succes a sistemului si d) timpul mediu de succes al sistemului.
2) Fie un sistem format din 5 componente independente. Se cunosc:
Intensitatea de reparare μi (i = 1,2,3,4,5);
Probabilitatile de succes pi (i = 1,2,3,4,5);
Traseele minimale T1 , T2 , T3 , T4 .
Se cer: a) probabilitatile de insucces qi (i = 1,2,3,4,5), b) taieturile minimale ale sistemului, c) probabilitatea de insucces a sistemului si d) timpul mediu de insucces al sistemului.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4011
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved