| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Efectul Joule-Thomson
Variatia de temperatura corespunzatoare unei detente isentalpice (detenta libera, laminare, efect Joule-Thomson) se calculeaza pe baza ecuatiei:

din care se deduce:
μJ.T. = efect diferential  (XVI.16)
(XVI.16)
Pentru gazul perfect μJ.T. = 0.
Efectul integral J.T. se calculeaza cu relatia:
 (XVI.16a)
(XVI.16a)
Ecuatiile (XVI.16) permit folosirea ecuatiilor de stare.
Intr-un calcul aproximativ se poate utiliza fie ecuatia:

numai pentru diferente mici de temperatura, fie ecuatia stabilita din ecuatia (XVI.10):

![]() fiind variatia de temperatura
corespunzatoare detentei J.T. de la o presiune mare la o presiune suficient de
mica pentru ca entalpia sa devina independenta de presiune si
fiind variatia de temperatura
corespunzatoare detentei J.T. de la o presiune mare la o presiune suficient de
mica pentru ca entalpia sa devina independenta de presiune si ![]() este valoarea medie a capacitatii calorice
dintre temperatura initiala si finala (se poate considera Cp initial).
este valoarea medie a capacitatii calorice
dintre temperatura initiala si finala (se poate considera Cp initial).
Exemplul 16. Sa se calculeze scaderea temperaturii aerului intr-o detenta libera (J.T.) de la 185,3 atm si 3,2 oC la 1,2 atm.
Rezolvare:
Rezolvand problema pe baza diagramei coeficientilor de activitate, se obtine notand γ1 si γ2 coeficientii de activitate la temperaturile reduse θ1 si θ2:

![]() ;
; ![]()
Pentru calcul se
aleg valorile ![]() si
si ![]() la care corespund
la care corespund ![]() si
si ![]()
Inlocuind valorile numerice, se obtine:

Valoarea experimentala este -39,6 oC.
Coeficientul diferential
al efectului J.T. poate avea valori pozitive si negative. Pentru ![]() , corespund
temperaturile de inversie Ti.
, corespund
temperaturile de inversie Ti.
Exemplul 17. Sa se stabileasca ecuatia curbei temperaturilor de inversie in functie de presiune, pentru un gaz Van der Waals.
Rezolvare:
a) Pentru T = Ti,
![]() si, conform ecuatiei (XVI.16), se obtine:
si, conform ecuatiei (XVI.16), se obtine:
![]() si deci
si deci ![]()
Din ecuatia lui Van der Waals:
![]() si
si ![]()
se obtine:
![]()
sau, cu notatia pV = y, rezulta:
3abp = y(2a-by)
In diagrama pV - p (fig. XVI.5) ecuatia care este reprezentata prin parabola J (v. si exemplul VII.13). Parabola B uneste minimul izotermelor.
Coordonatele varfului J sunt calculate din conditia (presiunea maxima la care se poate obtine o racire prin efectul J.T.):
![]() , de unde
, de unde ![]() ;
; ![]()
care corespund la ![]() ,
, ![]() .
.
Pentru pM =
0, rezulta ![]() si
si ![]() ,
(temperatura maxima la care se poate obtine o racire prin efect J.T.).
,
(temperatura maxima la care se poate obtine o racire prin efect J.T.).
b) Utilizand ecuatia redusa a lui Van der Waals:

si conditia ![]() , deci
, deci  , prin
eliminarea lui π se obtine:
, prin
eliminarea lui π se obtine:

si prin eliminarea lui θ:
![]()
Din ultimele ecuatii, eliminand pe φ, temperatura de inversie redusa in functie de presiunea redusa este data de ecuatia:
![]()
(cele doua temperaturi de inversie corespunzatoare lui π).

Fig. XVI.5. Curba de inversiune Joule-Thomson
Exemplul 18. Sa se calculeze temperaturile de inversie ale coeficientului Joule-Thomson pentru azot la 100 atm, presupunand valabila ecuatia de stare Beattie-Bridgeman.
Rezolvare:
Deoarece

din ecuatia de stare rezulta:
![]()
Intr-o prima aproximatie, neglijand termenul cu p2, rezulta:

de unde, pentru p = 100 atm, Ti = 589, respectiv 44 K. Pentru p = 1 atm, Ti = 656 K.
*Exemplul 19. Presupunand ca hidrogenul preracit la temperatura de topire a azotului (63,1 K) este supus pentru lichefiere unei detente Joule-Thomson, sa se calculeze presiunea optima la care trebuie sa se comprime hidrogenul si fractia maxima de hidrogen lichefiabil in aceste conditii.
Rezolvare:
Problema se rezolva in urmatoarele etape de calcul:
a) Ecuatia ![]() stabilita experimental, permite calculul
presiunii sau temperaturii de inversie
(valori reduse), α fiind egal cu
stabilita experimental, permite calculul
presiunii sau temperaturii de inversie
(valori reduse), α fiind egal cu ![]() .
.
Pentru presiunea de inversie corespunzatoare temperaturii de 63,1 K, datele critice ale hidrogenului fiind Tc = 33,2 K, pc = 12,8 atm si α = 3,27, se obtine valoarea:
![]()
b) Deoarece pentru
o destindere Joule-Thomson ![]() , notand cu
H1 entalpia
unui mol de gaz la presiunea initiala mare p1
si temperatura initiala T1,
cu H2 entalpia unui mol de
gaz la presiunea finala p2
si temperatura T2 si
cu Hl entalpia unui mol de
lichid, care fierbe la temperatura Tf
corespunzatoare presiunii de saturatie p2, se poate scrie:
, notand cu
H1 entalpia
unui mol de gaz la presiunea initiala mare p1
si temperatura initiala T1,
cu H2 entalpia unui mol de
gaz la presiunea finala p2
si temperatura T2 si
cu Hl entalpia unui mol de
lichid, care fierbe la temperatura Tf
corespunzatoare presiunii de saturatie p2, se poate scrie:
![]()
x fiind fractiunea condensata dintr-un mol:
![]()
Considerand zero entalpia lichidului, rezulta:
![]()
Entalpia unui mol de gaz la presiunea p si temperatura T care se refera la energia punctului de zero, se poate calcula prin relatia:

in care ![]() reprezinta capacitatea calorica molara a
gazului la presiunea de 1 atm sau mai mica.
reprezinta capacitatea calorica molara a
gazului la presiunea de 1 atm sau mai mica.
Prin urmare:


si deci:


in care μ
este coeficientul J.T.![]()
Integrala 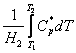 ,
aproximativ proportionala cu
,
aproximativ proportionala cu ![]() si practic neinfluentata de presiune, are o
valoare mica si astfel:
si practic neinfluentata de presiune, are o
valoare mica si astfel:

Problema determinarii temperaturii si presiunii la care x este maxim poate fi rezolvata daca se cunosc valorile μ si Cp in functie de temperatura, sau daca se cunoaste o ecuatie de stare exacta a gazului, pentru inlocuirea termenilor in a doua integrala.
Conditia de maxim este data de relatiile:
![]() si
si 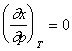
Pentru a rezolva aceste ecuatii este necesara cunoasterea unei ecuatii exacte de stare in domeniul de temperatura si presiune a maximului si, deoarece acesta nu poate fi cazul obisnuit, se prefera calcului lui x prin integrare grafica, pentru valorile de temperatura si presiune fixate de experienta. Pentru alegerea conditiilor initiale de lucru, considerand presiunea finala egala cu 1 atm, conditia de maxim a lui

este data de ecuatia:
![]()
Rezulta ca valoarea
maxima a lui x se obtine cand
presiunea initiala corespunde presiunii de inversie pentru temperatura initiala
aleasa, deoarece aceasta conditie reprezinta si ![]() .
.
Pentru datele problemei presiunea initiala trebuie sa fie, deci, pi = 146 atm.
c) Pentru calculul fractiunii x lichefiate se poate utiliza si ecuatia (modificata) Beattie-Bridgeman:
![]()
in care:
![]()
![]()
![]()
Valori pentru H2:

Rezulta ![]() ,
, ![]() ,
, ![]() si
si

si, prin integrare, se obtine:
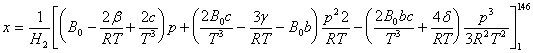
H2 este entalpia unui mol de hidrogen la 63,1 K si 1 atm care se refera la entalpia unui mol lichid la temperatura normala la fierbere. Caldura de vaporizare a hidrogenului este 216 cal mol-1 la 20,4 K.
Diferenta dintre entalpia
unui mol de gaz la 63,1 si 20,4 K este ![]() si deci
si deci ![]() (aici s-a neglijat diferenta de energie
interna a amestecului 3:1 de orto- si parahidrogen intre aceste doua
temperaturi).
(aici s-a neglijat diferenta de energie
interna a amestecului 3:1 de orto- si parahidrogen intre aceste doua
temperaturi).
Rezulta:
![]()
Conform acestui rezultat, fractiunea maxima de hidrogen lichefiabil pentru o temperatura initiala de 63,1 K este 0,414, deci 41,4%.
Observatie: Sa se rezolve aceeasi problema utilizand ecuatia de stare a lui Berthelot. In acest caz se obtine x = 0,80.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2417
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved