| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Compunerea miscarilor oscilatorii armonice
Pe baza legilor micarii oscilatorii armonice ideale se pot studia miscari oscilatorii mai complexe, care rezulta din compunerea a doua sau mai multe oscilatii armonice, care se desfasoara pe directii paralele sau pe directii perpendiculare.
1. Compunerea oscilatiilor armonice paralele de aceeasi pulsatie
Sa presupunem ca un punct material de masa m este legat de doua resorturi elastice, aa cum se vede n fig.3.5, fiind supus simultan la doua forte elastice pe aceeai directie dar în sensuri diferite. Cele doua resorturi elastice sunt identice, adica au aceeai constanta elastica, k 1 = k 2 = k.
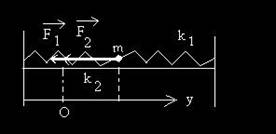
Fig.3.5. Oscilatie armonica sub actiunea a doua forte elastice paralele.
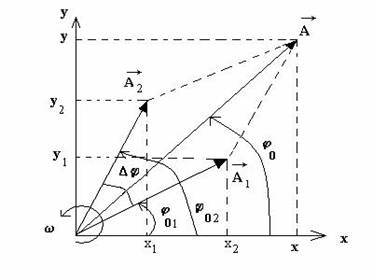
Fig. 3.6. Reprezentarea fazoriala a compunerii oscilatiilor paralele.
2. Compunerea oscilatiilor armonice paralele de frecventa diferita
Consideram doua oscilatii armonice individuale ale punctului material de masa m. Una dintre oscilatii are pulsatia proprie 1 iar cealalta are pulsatia proprie 2. Diferenta dintre cele doua frecvente de oscilatie nu este însa prea mare. Elongatiile celor doua oscilatii armonice independente sunt de forma:
Punctul material este supus simultan ambelor oscilatii, asa cum se poate vedea în fig. 3.7, si ne propunem sa determinam ecuatia oscilatiei rezultante.
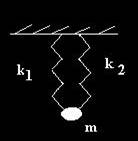
Fig. 3.7. Compunerea a doua oscilatii paralele de frecvente diferite.
Tb mai este numita si perioada batailor.

Fig. 3.8. Fenomenul de batai.
Faza oscilatiei are perioada T, mult mai mica dec t Tb:
Oscilatia rezultanta este reprezentata, în fig.3.7, cu linie continua.
Perioada batailor este intervalul de timp între doua treceri succesive ale amplitudinii rezultante prin valoarea minima sau maxima.
3. Compunerea oscilatiilor perpendiculare
Consideram un punct material de masa m, care care este solicitat simultan sa oscileze armonic sub actiunea a doua resorturi elastice identice legate pe doua directii perpendiculare, ca n fig. 3.9.
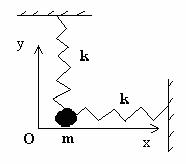
Fig. 3.9. Compunerea oscilatiilor perpendiculare
Cele doua miscari oscilatorii armonice sunt perpendiculare, av nd ecuatiile elongatiilor pe cele doua directii de forma
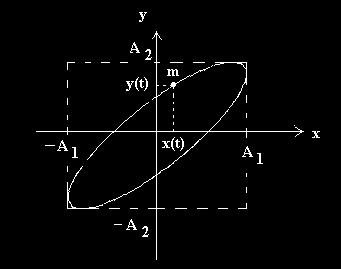
Fig. 3.10. Traiectorie eliptica rotita fata de axe.

Fig. 3.11. Traiectorie particulara în cazul compunerii oscilatiilor perpendiculare n faza,
Elipsa care descrie traiectoria particulei nu mai este rotita fata de axele de coordonate (vezi fig.3.12).
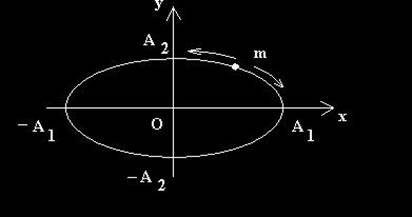
Fig.3.12. Traiectoria rezultata din compunerea a doua oscilatii perpendiculare în cuadratura de faza,
Micarea punctului material se defasoara pe elipsa, într-un sens sau n altul.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 281
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved