| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Notiuni de baza în analiza vectoriala
Operatiunile de baza din analiza vectoriala sunt pe de o parte derivarea si diferentierea marimilor vectoriale, precum si operatiunea inversa – integrarea, respectiv gasirea functiei vectoriale când se cunosc derivatele acesteia.
Regulile dupa care se fac aceste operatiuni sunt asemanatoare celor întâlnite la functiile scalare; sunt necesare unele precizari legate de operatiunile cu vectori descrise în paragraful precedent.
1 Derivata si diferentiala unei functii vectoriale
Se
considera functia vectoriala ![]() având ca variabila
scalara independenta parametrul
având ca variabila
scalara independenta parametrul ![]() . În marea lor
majoritate variatiile marimilor vectoriale ale Mecanicii sunt în
raport cu timpul astfel ca simbolul considerat pentru exemplificare nu
este ales întâmplator.
. În marea lor
majoritate variatiile marimilor vectoriale ale Mecanicii sunt în
raport cu timpul astfel ca simbolul considerat pentru exemplificare nu
este ales întâmplator.
Daca
functia ![]() este continua si
neteda pe un interval cuprins între
este continua si
neteda pe un interval cuprins între ![]() si
si ![]() , derivata vectorului în raport cu
, derivata vectorului în raport cu ![]() se defineste
prin relatia:
se defineste
prin relatia:
![]() (2.48)
(2.48)
Prin ![]() s-a notat variatia
finita a vectorului
s-a notat variatia
finita a vectorului ![]() corespunzatoare
intervalului respectiv. Daca si
functia
corespunzatoare
intervalului respectiv. Daca si
functia ![]() este continua si
neteda pe acelasi interval se defineste asemanator si
cea de a doua derivata a vectorului
este continua si
neteda pe acelasi interval se defineste asemanator si
cea de a doua derivata a vectorului ![]() . Astfel:
. Astfel:
![]() (2.49)
(2.49)
În Mecanica se utilizeaza în general derivate pâna la ordinul II.
Daca parametrul în raport cu care se face derivarea este timpul, atunci se obisnuieste o marcare specifica a derivatelor:
![]() (2.50)
(2.50)
Aceeasi
marcare se aplica si derivatelor marimilor scalare, de exemplu ![]() , etc.
, etc.
Presupunând
ca functia vectoriala ![]() este dependenta
de t printr-o variabila scalara
intermediara,
este dependenta
de t printr-o variabila scalara
intermediara, ![]() si
si ![]() , derivata în raport cu t
urmeaza regula de la functiile scalare
, derivata în raport cu t
urmeaza regula de la functiile scalare
![]() (2.51)
(2.51)
Daca
vectorul ![]() se raporteaza la
un sistem de referinta fix, de exemplu Oxyz, în expresia analitica
se raporteaza la
un sistem de referinta fix, de exemplu Oxyz, în expresia analitica
![]() (2.52)
(2.52)
versorii
![]() sunt constanti si
derivare se aplica proiectiilor pe axe:
sunt constanti si
derivare se aplica proiectiilor pe axe:
 (2.53)
(2.53)
Cazul în
care versorii ![]() apartin unui
sistem de referinta mobil si sunt prin urmare variabili în timp
ca directie va fi tratat separat în partea de Cinematica.
apartin unui
sistem de referinta mobil si sunt prin urmare variabili în timp
ca directie va fi tratat separat în partea de Cinematica.
Variatia finita ![]() a vectorului
a vectorului ![]() , corespunzatoare unei variatii
, corespunzatoare unei variatii ![]() a variabilei
independente se poate scrie în functie de variatiile proiectiilor
a variabilei
independente se poate scrie în functie de variatiile proiectiilor
![]() (2.54)
(2.54)
Variatia
infinitezimala, respectiv diferentiala vectorului ![]() , corespunzatoare unei variatii infinitezimale
, corespunzatoare unei variatii infinitezimale ![]() , se exprima printr-o relatie asemanatoare:
, se exprima printr-o relatie asemanatoare:
![]() (2.55)
(2.55)
Daca vectorul ![]() este o functie de
doua variabile scalare
independente, respectiv
este o functie de
doua variabile scalare
independente, respectiv
![]() (2.56)
(2.56)
si sistemul de referinta este fix, se pot calcula derivatele partiale de ordinul I:
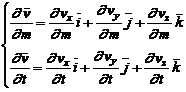 (2.57)
(2.57)
În mod
analog se calculeaza si derivatele de ordin superior. Diferentiala
totala a vectorului, corespunzatoare
variatiilor infinitezimale ![]() si
si ![]() , are forma:
, are forma:
![]() (2.58)
(2.58)
În acelasi mod se obtin derivatele partiale si diferentiala unui vector functie de mai multe variabile scalare independente, necesare în Mecanica analitica.
2 Interpretari geometrice
În sistemul de referinta
Oxyz din fig. 2.14 vârful vectorului ![]() va descrie o curba
(C) în spatiu. Între
momentele
va descrie o curba
(C) în spatiu. Între
momentele ![]() si
si ![]() variatia
variatia ![]() va uni vârfurile
vectorilor corespunzatori celor doua momente, respectiv punctele M si M1. La limita, când
va uni vârfurile
vectorilor corespunzatori celor doua momente, respectiv punctele M si M1. La limita, când ![]() , punctul M1
tinde catre M iar dreapta MM1 va deveni tangenta la
curba (C) în M. Vectorul derivatei
, punctul M1
tinde catre M iar dreapta MM1 va deveni tangenta la
curba (C) în M. Vectorul derivatei ![]() , definit prin relatia (2.48), va avea deci directia
tangentei la aceasta curba si sensul în concordanta cu
deplasarea vârfului vectorului pe curba. n fig. 2.15 este reprezentata situatia
frecventa în care curba (C) si
vectorul
, definit prin relatia (2.48), va avea deci directia
tangentei la aceasta curba si sensul în concordanta cu
deplasarea vârfului vectorului pe curba. n fig. 2.15 este reprezentata situatia
frecventa în care curba (C) si
vectorul ![]() sunt coplanare în
planul xOy.
sunt coplanare în
planul xOy.
|
Fig. 2.14 |
|
Fig. 2.15 |
3 Reguli de derivare vectoriala
Regulile de derivare în cadrul unor operatiuni cu vectori sunt analoge celor efectuate cu marimi scalare. n relatiile (2.59) sunt grupate cele mai frecvente operatiuni de derivare în raport cu variabila t întâlnite în Mecanica.
 (2.59)
(2.59)
Regulile
de diferentiere sunt analoge acestora, relatiile uzuale obtin ndu-se prin suprimarea termenului ![]() .
.
4 Integrarea functiilor vectoriale
Integrala nedefinita a functiei
vectoriale ![]() se exprima prin
relatia:
se exprima prin
relatia:
![]() (2.60)
(2.60)
în care ![]() este functia
primitiva de determinat iar
este functia
primitiva de determinat iar ![]() este o constanta
vectoriala de integrare a carei expresie se calculeaza în functie
de conditiile concrete impuse.
este o constanta
vectoriala de integrare a carei expresie se calculeaza în functie
de conditiile concrete impuse.
Daca
functia ![]() este integrabila
pe un interval cuprins între valorile
este integrabila
pe un interval cuprins între valorile ![]() si
si ![]() , integrala
definita a
acestei functii va fi:
, integrala
definita a
acestei functii va fi:
![]() (2.61)
(2.61)
Considerând
pentru vectorii ![]() ,
, ![]() si
si ![]() exprimari
analitice corespunzatoare, integrala nedefinita (2.60) devine:
exprimari
analitice corespunzatoare, integrala nedefinita (2.60) devine:
 (2.62)
(2.62)
Rezulta relatiile scalare:
![]() (2.63)
(2.63)
În acelasi mod se deduc si relatiile scalare provenite din integrala definita (2.61):
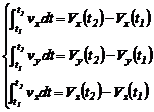 (2.64)
(2.64)
În cazul
unei functii vectoriale de doua
variabile independente ![]() integrarea se poate
efectua în raport cu oricare dintre acestea, cealalta comportându-se ca o
constanta.
integrarea se poate
efectua în raport cu oricare dintre acestea, cealalta comportându-se ca o
constanta.
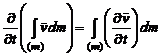 (2.65)
(2.65)
Operatiunea de derivare în raport cu t este independenta fata de integrarea în raport cu variabila m. Relatia aceasta este utila în Dinamica solidului rigid relativ la teorele generale.
5 Reguli de integrare vectoriala
Facând abstractie de constantele de integrare, relativ la operatiunile cu vectori se pot mentiona unele reguli de integrare, dupa cum urmeaza:
 (2.66)
(2.66)
Pentru integrarea unui singur vector relatiile (2.63) si (2.64) “transfera” operatiunile la nivelul proiectiilor, fiind valabile regulile generale de integrare ale marimilor scalare.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 403
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved