| CATEGORII DOCUMENTE |
Model liniar unifactorial
Se cunosc urmatoarele date privind productia (miliarde lei) alimentelor si bauturile precum si consumul intermediar (miliarde lei) pentru anii 1990-2004.
|
Anul |
Productia (miliarde lei) |
Consumul intermediar (miliarde lei) |
Se cere :
a. Sa se specifice modelul econometric ce descrie legatura dintre cele doua variabile.
b. Sa se estimeze parametrii modelului si sa se calculeze valorile teoretice ale variabilei endogene.
c. Sa se verifice ipotezele de fundamentare a metodei celor mai mici patrate.
d. Sa se verifice semnificatiile estimatorilor si verosimilitatea modelului.
Rezolvare :
a)
Pe baza datelor problemei se poate construi un model econometric
unifactorial de forma:
y f (x ) u
unde:
y = valorile reale ale variabilelor dependente;
x = valorile reale ale variabilelor independente;
u = variabila reziduala, reprezentand influentele celorlalti
factori ai variabilei y, nespecificati in model, considerati factori intamplatori, cu influente nesemnificative asupra variabilei y.
Analiza datelor din tabel, in raport cu procesul economic descris
conduce la urmatoarea specificare a variabilelor:
y = capacitatea de cazare turistica in functiune, reprezentand
variabila rezultativa (endogena);
x = numarul de innoptari, reprezentind variabila factoriala
(exogena), respectiv factorul considerat prin ipoteza de lucru cu influenta cea mai puternica asupra variabilei y.
Specificarea unui model econometric presupune, de asemenea,
alegerea unei functii matematice tice f x cu ajutorul careia poate fi descrisa legatura dintre cele variabile. In cazul unui model unifactorial, procedeul cel mai des folosit il constituie reprezentarea grafica a celor doua siruri de valori cu ajutorul corelogramei - vezi figura 1.
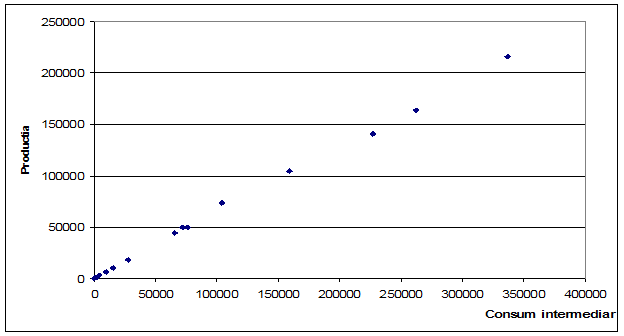 Figura 1. Legatura dintre productia (miliarde
lei) si consumul intermediar (miliarde lei) din Romania
Figura 1. Legatura dintre productia (miliarde
lei) si consumul intermediar (miliarde lei) din Romania
Din grafic se poate observa ca distributia punctelor empirice (xt ,yt) poate fi aproximata cu o dreapta. Ca atare, modelul econometric care descrie legatura dintre cele doua variabile se transforma intr-un model liniar unifactorial y a bx u a si b reprezentand parametrii modelului, b 0 , panta dreptei fiind pozitiva deoarece legatura dintre cele doua variabile este liniara.
b)Deoarece parametrii modelului sunt necunoscuti, valorile acestora se pot estima cu ajutorul mai multor metode, in mod curent fiind folosita insa metoda celor mai mici patrate (M.C.M.M.P.).
Utilizarea acestei metode porneste de la urmatoarea relatie:
![]() ;
; ![]()
![]() ;
;
![]()
unde:
![]() = valorile
teoretice ale variabilei y obtinute numai in functie de
valorile
= valorile
teoretice ale variabilei y obtinute numai in functie de
valorile
factorului esential x si de valorile estimatorilor parametrilor a si b,
respectiv ![]() si
si ![]() ;
;
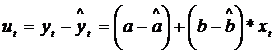 = estimatiile valorilor variabilei
reziduale
= estimatiile valorilor variabilei
reziduale
In mod concret, M.C.M.M.P. consta in a minimiza functia:
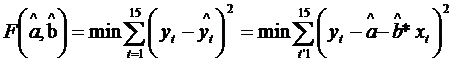
Conditia de minim a acestei functii rezulta din:
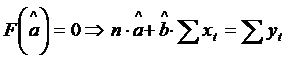
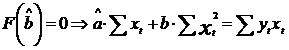
|
Nr. crt. |
|
|
|
|
|
|
| |||||
|
Total |
Tabel 1
|
|
|
|
|
|
|
|
| |||||
Tabel 1 (continuare)
|
|
|
|
|
|
|
|
Tabel 1 (continuare)
Estimarea
parametrului ![]() :
:
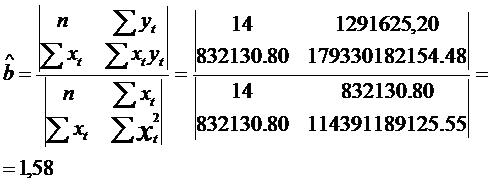
(vezi calcule in tabelul 1, coloanele 1,2,3,4)
Estimarea parametrului ![]() :
:
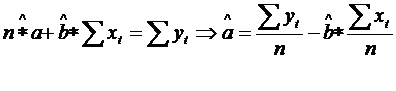
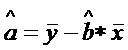
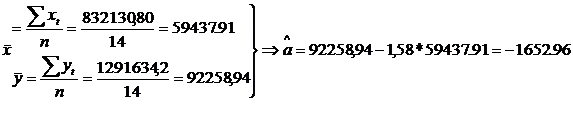
Dispunand de
estimatiile parametrilor se pot calcula valorile teoretice (estimate) ale
variabilei endogene, ![]() ,cu ajutorul
relatiei:
,cu ajutorul
relatiei:
![]() (vezi tabelul 1,
coloana 5).
(vezi tabelul 1,
coloana 5).
Valorile variabilei reziduale vor rezulta din urmatoarea relatie
![]() (vezi tabelul 1,coloana 8).
(vezi tabelul 1,coloana 8).
Pe baza acestor
valori se pot calcula abaterea medie patratica a variabilei reziduale
![]() si abaterile medii patratice ale
celor doi estimatori,
si abaterile medii patratice ale
celor doi estimatori, ![]() si
si ![]() :
:
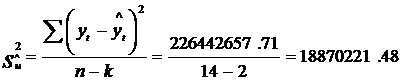
(vezi tabelul 1, coloana 9)
unde:
k = numarul parametrilor.
![]()
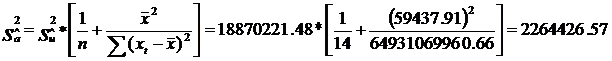
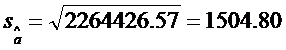
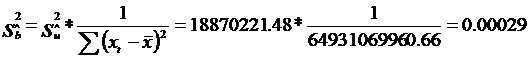 -
-
![]()
In urma acestor calcule, modelul econometric se poate scrie:
![]() ;
; ![]()
(1504.80) (0.017)
c) Estimatorii obtinuti cu ajutorul M.C.M.M.P. sunt estimatori de maxima verosimilitate daca pot fi acceptate urmatoarele ipoteze:
c1) Variabilele observate nu sunt afectate de erori de masura.
Aceasta conditie se poate verifica cu regula celor trei sigma, regula care consta in verificarea urmatoarelor relatii:
![]() ;
; ![]()
Pe baza datelor din tabelul 1, coloanele 7, 11, se obtin:
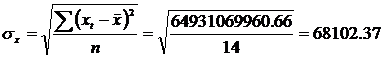
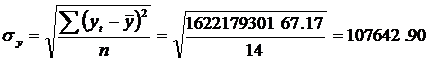
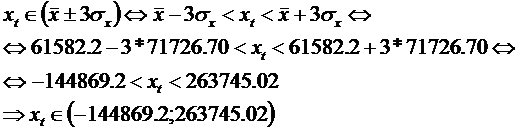
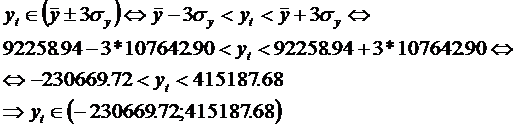
Deoarece
valorile acestor variabile apartin intervalelor ![]() si
si
![]() , ipoteza de mai sus poate fi acceptata fara
rezerve.
, ipoteza de mai sus poate fi acceptata fara
rezerve.
c2) Variabila aleatoare (reziduala) ![]() este de medie nula
este de medie nula ![]() ,
,
iar
dispersia ei, ![]() , este
, este
Acceptarea ipotezei se poate face prin intermediul mai multor procedee:
c2.1) Procedeul grafic - care consta in
construirea corelogramei privind valorile variabilei factoriale x si
ale variabilei reziduale ![]() (vezi figura 2).
(vezi figura 2).
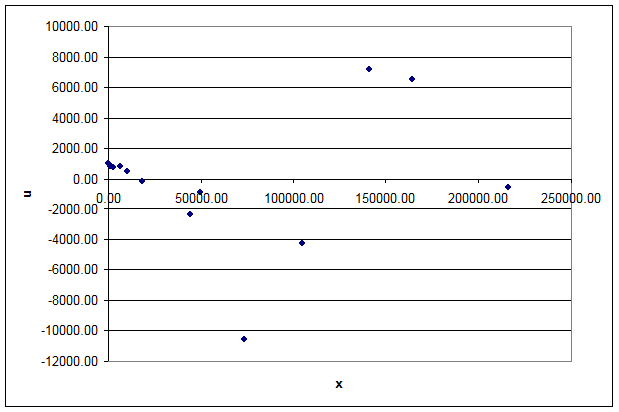 Figura 2
Figura 2
Deoarece graficul punctelor empirice prezinta o distributie oscilanta, se poate accepta ipoteza ca cele doua variabile sunt independente si nu corelate.
c2.2.) Acceptarea sau respingerea ipotezei de homoscedasticitate cu
ajutorul analizei variatiei (vezi punctul d)).
c3) Valorile
variabilei reziduale ![]() sunt independente,
respectiv nu exista fenomenul de autocorelare. Acceptarea sau respingerea
acestei conditii se poate face cu:
sunt independente,
respectiv nu exista fenomenul de autocorelare. Acceptarea sau respingerea
acestei conditii se poate face cu:
c3.1.) Procedeul grafic - corelograma intre valorile
variabilei dependente ![]() si
valorile variabilei reziduale
si
valorile variabilei reziduale ![]() (vezi figura 3).
(vezi figura 3).
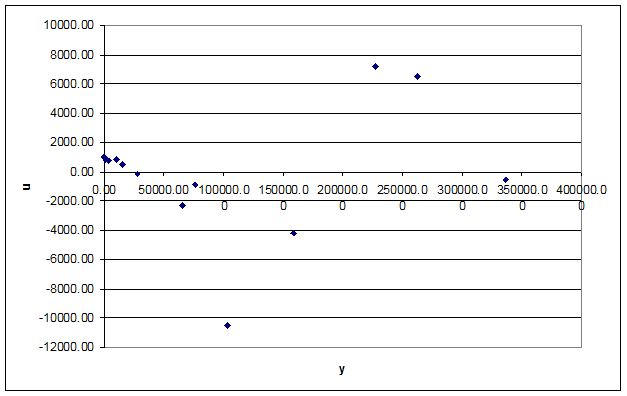 Figura 3
Figura 3
c3.2.) Testul Durbin-Watson consta in calcularea termenului empiric:
![]()
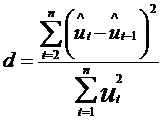
si compararea acestei marimi " d " cu doua valori teoretice, d1 si d2 , preluate din tabela Durbin-Watson (vezi Anexa 3) in functie de un prag de semnificatie , arbitrar ales, de numarul variabilelor exogene k si de valorile observate n,n
Acceptarea sau respingerea ipotezei de independenta a erorilor se bazeaza pe o anumita regula, care consta in:
daca ![]() autocorelare
pozitiva;
autocorelare
pozitiva;
- daca ![]() indecizie,
recomandandu-se acceptarea autocorelarii pozitive;
indecizie,
recomandandu-se acceptarea autocorelarii pozitive;
- daca ![]() erorile sunt
independente;
erorile sunt
independente;
- daca ![]() indecizie,
recomandandu-se acceptarea
indecizie,
recomandandu-se acceptarea
autocorelarii negative;
- daca ![]() autocorelare
negativa.
autocorelare
negativa.
Pe baza datelor problemei, valoarea empirica a variabilei Durbin-Watson este:
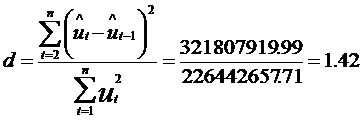
Lucrand cu un prag de semnificatie ![]() , numarul variabilelor exogene fiind
, numarul variabilelor exogene fiind ![]() , iar numarul observatiilor
, iar numarul observatiilor ![]() , din tabela
distributiei Durbin-Watson se citesc valorile (pentru cazul
, din tabela
distributiei Durbin-Watson se citesc valorile (pentru cazul ![]() )
) ![]() si
si ![]() .
.
Deoarece ![]() ,se poate preciza ca erorile sunt independente
,se poate preciza ca erorile sunt independente
c3.3.) Coeficientul de autocorelatie de ordinul 1
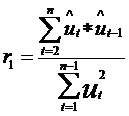
Se poate demonstra ca intre coeficientul de autocorelatie de ordinal 1 si variabila Durbin-Watson exista relatia:
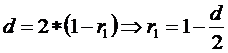
Stiind ca:

Calculul coeficientului de autocorelatie de ordinul 1:
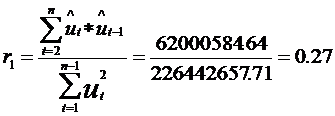
Deoarece ![]() , si acest indicator arata ca ipoteza de
independenta a valorilor variabilei reziduale poate fi acceptata.
, si acest indicator arata ca ipoteza de
independenta a valorilor variabilei reziduale poate fi acceptata.
c4) Verificarea ipotezei de normalitate a valorilor variabilei reziduale
Se
stie ca, daca erorile urmeaza legea normala de medie
zero si de abatere medie patratica ![]() (consecinta
ipotezelor c1, c2, c3), atunci are loc relatia:
(consecinta
ipotezelor c1, c2, c3), atunci are loc relatia:
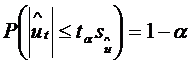
Pe baza acestei relatii, in functie de diferite praguri de
semnificatie ![]() , din tabela distributiei normale se vor prelua valorile
corespunzatoare ale lui
, din tabela distributiei normale se vor prelua valorile
corespunzatoare ale lui ![]() .
.
Lucrand cu un prag de semnificatie
![]() ,din tabela distributiei Student n <
se preia
valoarea variabilei, cu un numar de grade de libertate
,din tabela distributiei Student n <
se preia
valoarea variabilei, cu un numar de grade de libertate ![]() ,
,![]() , iar pentru un prag de semnificatie
, iar pentru un prag de semnificatie ![]() , avem
, avem ![]() . Cu ajutorul acestor date, verificarea ipotezei de
normalitate se poate face pe baza urmatorului graphic (Figura 4.): pe axa
Ox se vor reprezenta valorile ajustate ale variabilei
. Cu ajutorul acestor date, verificarea ipotezei de
normalitate se poate face pe baza urmatorului graphic (Figura 4.): pe axa
Ox se vor reprezenta valorile ajustate ale variabilei ![]() ,
, ![]() , iar pe axa Oy se vor trece valorile variabilei
reziduale
, iar pe axa Oy se vor trece valorile variabilei
reziduale ![]() .
.
Se observa ca valorile empirice ale variabilei reziduale se
inscriu in banda construita, cu un prag de semnificatie ![]() .Ca atare, ipoteza de normalitate a variabilei reziduale
poate fi acceptata cu acest prag de semnificatie.
.Ca atare, ipoteza de normalitate a variabilei reziduale
poate fi acceptata cu acest prag de semnificatie.
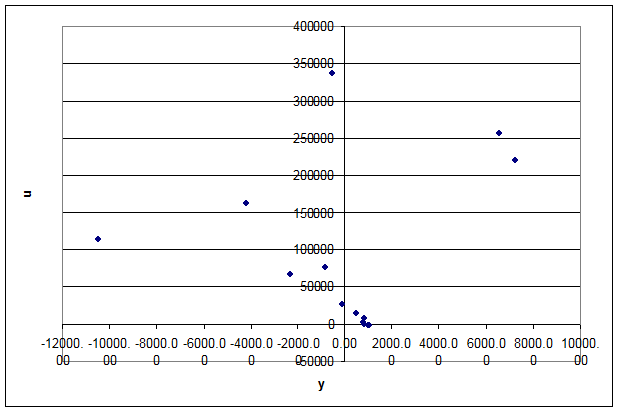
Figura 4
d) Verificarea semnificatiei estimatorilor si a verosimilitatii modelului
d1) Verificarea semnificatiei estimatorilor
Estimatorii sunt semnificativ diferiti de zero, cu un prag de
semnificatie ![]() , daca se verifica urmatoarele relatii:
, daca se verifica urmatoarele relatii:
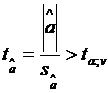 ;
; 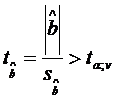
Stiind ca (vezi punctul b) al
problemei) ![]() ,
, ![]() ,
, ![]() ,
, ![]() si, lucrand cu un
prag de semnificatie
si, lucrand cu un
prag de semnificatie ![]() , din tabela
distributiei Student se preia valoarea
, din tabela
distributiei Student se preia valoarea ![]() .
.
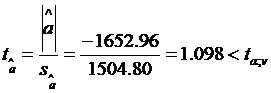
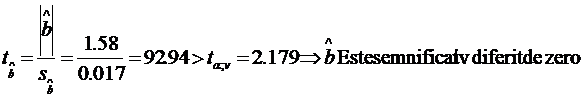
d2) Verificarea verosimilitatii modelului
Pentru a accepta ipoteza de liniaritate se calculeaza coeficientul de corelatie liniara:
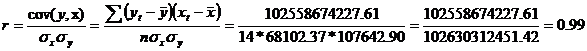
Coeficientul de corelatie liniara fiind definit in intervalul [-1;1] , rezulta ca valoarea obtinuta de 0.99 indica o puternica corelatie liniara intre cele doua variabile. Verificarea verosimilitatii modelului se face cu ajutorul analizei dispersionale (analiza variatiei).
|
Sursa de variatie |
Masura variatiei |
Nr gradelor de libertate |
Dispersii corectate |
Valoarea testului "F" |
|
|
Fc |
Fα;v1;v2 |
||||
|
Varianta dintre grupe |
|
k-1=1 |
|
|
|
|
Varianta reziduala |
|
n-k=12 |
| ||
|
Varianta totala |
|
n-1=13 | |||
Testul Fisher-Snedecor indica faptul ca rezultatele obtinute sunt semnificative pentru un prag de semnificatie de 5%: Fc=8589.93> F0.05;12=4.76.
Pe baza datelor din tabelul de mai sus se poate calcula raportul de corelatie dintre cele doua variabile:
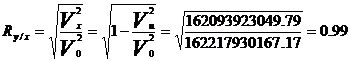
Se poate demonstra ca, in cazul unei legaturi liniare, raportul de corelatie este egal cu coeficientul de corelatie liniara:
![]()
Verificarea semnificatiei raportului de corelatie si, implicit, a coeficientului de corelatie liniara se face cu ajutorul testului Fisher- Snedecor:
![]() , R fiind semnificativ daca
, R fiind semnificativ daca ![]() .
.
![]()
Deoarece raportul de corelatie este semnificativ diferit de zero, cu
un prag de semnificatie ![]() , rezulta modelul
econometric:
, rezulta modelul
econometric:
![]() ;
; ![]()
R=0.99
d=1.42
care descrie corect dependenta dintre cele doua variabile, acesta explicand 99,05% din variatia totala a variabilei dependente, adica variatia productiei se datoreaza in proportie de 99,05% valorii adaugate brute.
![]()
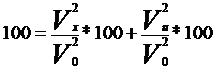
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3078
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved