ALGORITMI DE PRELUCRARE SECVENTIALA A DATELOR STATISTICE

ALGORITMI DE PRELUCRARE SECVENTIALA A DATELOR STATISTICE

In acest capitol se prezinta algoritmii de prelucrare secevntiala a datelor statistice pe baza testului secvential a lui Wald. Algoritmii sunt utilizati in prelucrarea datelor de control statistic pe masura ce se obtin si a datelor statistice din analizele chimice ce indica prezenta sau absenta unui element chimic.Vom pastra notatia din statistica clasica

1. Introducere

In problemele de decizie secventiala se opereaza succesiv asupra termenilor sirului de observatii pe masura ce se obtin. Structura statistica a observatiilor este data de o structura statistica secventiala normala sau binomiala. Problema de decizie secventiala cea mai mult aplicata este aceea a carei regula de decizie (functie de decizie) utilizeaza raportul de probabilitate si are structura urmatoare:

.

unde:

d₁ = decizia ca starea adevarata este q

d₂ = decizia ca starea adevarata este q

d₃ = decizia de a continua experienta .

unde

iar s(w,n) =

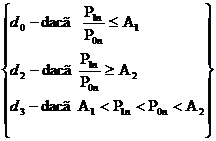
unde iar si sunt erorile de primul si al doilea gen.

2. Decizii statistice secventiale cu structura statistica a observatiilor normala

Consideram cazul cand elementul aleator X are densitatea de probabilitate

unde m poate lua una din valorile m₀ sau m₁.

In acest caz obtinem urmatoarea problema de decizie secventiala:

.

unde:

d₁ este decizia ca m = m₀;

d₂ este decizia ca m = m₁;

d₃ este decizia de continuare a selectiei.

Functia de decizie S se deduce din expresia raportului probabilitatilor P_ln/ P_on si are urmatoarea forma:

iar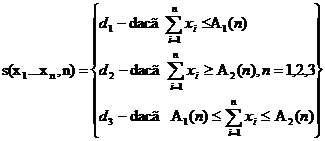

unde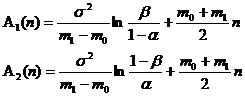

iar si sunt erorile de prima si a doua speta

Rezolvarea acestei probleme se reduce la calcularea lui S (x_l,.. x_n) pentru n = 1,2,., pana cand ia valoarea d₁ sau d₂.

Algoritmul prezentat mai jos permite rezolvarea problemelor de decizie secventiala cu structura statistica a observatiilor normala

0 START [Decizii-Secventiale cu observatii dintr-o populatie-normala]

1 INPUT

2

3

4

5

6

7

WHILE K = 0

8.1 INPUT

8.2 S ← S+ En

8.3 A₁←a+n*c

8.4 A₂←b+n*c

8.5 If A₁<S<A₂

Then

.1 n n +1

Else

.2 IF S ≤ A₁

Then

.1 K

Else

.2 K ← 2

.3 CONTINUE

CONTINUE

CASE k OF

9.1 OUTPUT

9.2 OUTPUT

STOP

3 Decizii statistice secventiale cu structura statistica a observatiilor binomiala

Consideram un fenomen a carui probabilitate de realizare p in urma unui experiment, poate lua doua valori distincte p₀ si p₁. Deci, in legatura cu acest fenomen se pot adopta deciziile:

d₀ : p = p₀

d₂ : p = p₁

d₃ : de continuare a experimentarii

Notam cu P₀ (m,n) = probabilitatea ca fenomenul sa apara de m ori din n experimente cand s-a adoptat decizia d₁ si cu P₁(m,n) = probabilitatea ca fenomenul sa se realizeze de m ori din n experimente cand s-a adoptat decizia d₂.

Problema de decizie statistica, secventiala cu structura statistica a observatiilor:

are urmatoarea forma:

Scriind inegalitatile procedurii secventiale a raportului probabilitatilor P₁(m,n)/P₀(m,n) obtinem urmatoarea expresie a functiei de decizie

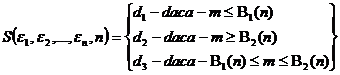
unde ε_i = 1 dac[ fenomenul s-a realizat la etapa i,

0 dac[ nu s-a realizat la etapa i.

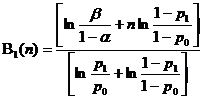
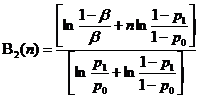
Algoritmul DeSeB este destinat rezolv[rii problemelor de decizie secveniale cu structura statistica a observaiilor binomiale

0 START[DeSeB]

1 INPUT

2 k←0,n←1,m←0

3 a ← ln[/(1-)

4 b ←ln[(1-p1)/(1-p0)]

5 c ← ln(p1/p0)-b

6 d ←ln[(1-

7 WHILE k = 0

7.1 INPUT

7.2 a₁ ←(a - nb)/c

7.3 a₂ ←(d - nb)/c

7.4 m ← m + E

7.5 IF a₁ < m < a₂

THEN

7.5.1 n ← n +1

ELSE

7.5.2 IF m < a₁

THEN

.1 k ← 1

ELSE

.2 k

7.5.3 CONTINUE

7.6 CONTINUE

8 CASE k OF

8.1 OUTPUT

8.2 OUTPUT

9 STOP

II Stabilitateaunui proces tehnologic relativ la caracteristicile de calitate ale unui produs

Pentru studiul statistic al stabilitatii unui process tehnologic se aplica testul Bartlett pentru egalitatea mai multor dispersii. In fiecare perioada i se fac n_i observatii asupra caracteristicilor de calitate, i= 1,2,..,k.

Procesul tehnologic se considera stabil daca este adevarata ipoteza:

Daca ipoteza H₀ este adevarata, atunci 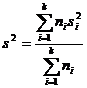este repartizata .

Astfel repartitia oricarei functii/sdepinde de n₁,n₂,.,n_k si b. Bartlett a aratat ca daca ipoteza H₀ este adevarata atunci statistica

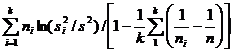
este repartizata ² cu k - 1 grade de libertate.

Date: k= numarul de serii de observatii; n_i = numarul de observatii ale seriei i, i = 1,2,.,k si x₁,x₂..x_ni, valorile observate in seria i, si din tabelul functiei X₁ cu k -1 grade de libertate se alege .

0 START [ Decizii Bartlet]

1 b ←0; c ←0

2 n← 0

3 s2← 0

4 INPUT [k, ,n_1,..,n_k]

5 FOR i=1,2,..,k

5.1 INPUT

5.3 s_i ←0

5.4 FOR j = 1,2,.,n_i

5.4.1

5.5

5.6 FOR j = 1,2,.,ni

5.6.1

5.7s_i←s_i/(n_i-1)

5.8 s2 ← s2 +n_i*s_i

5.9 n ← n+n_i

6 s₂ ← s₂/n

7 FOR i=1,2,.,k

7.1 b← b+n_i*ln(s_i/s₂)

7.2 c ← c+(1/n_i -l/n)

8 R ← b/(1+b/(k - 1))

9 IF R <.

Then

9.1 OUTPUT

Else

9.2 OUTPUT

10 STOP

II.2 Algoritm de apreciere a stabilitatii in functionare a masinilor unelte cu comanda numerica

In cazul cand numarul de masuratori este acelasi in k selectii se aplica testul lui Cochran care este mai rapid decat testul lui Bartlett si care consta in urmatoarele:

se calculeaza dispersiile de selectie:

- se calculeaza max s_i 1 i k

se formeaza raportul,

din tabela se extrage

daca se respinge ipoteza omogenitatii dispersiilor, adica a stabilitatii in functionare a masinilor unelte cu comanda numerica

Date de modelare:

K = numarul de selectii observate ale caracteristicii calitative a unui produs;

n_i -n numarul de valori observate in etapa i i= 1,2,.,k;

x₁, x₂,..,x_n - valorile de selectie la o anumita etapa i; i= 1,2,.n;

- pragul (nivelul) de acceptare ( = 0,05).

Reproducem exemplul dat in in care se studiaza stabilitatea in functionare a unei masini de alezat si frezat cu comanda numerica. Intr-un table sunt inregistrate erorile obtinute in urma masurarii deplasarilor dupa axele de coordonate ox si oy ale masinii.

0 START[TeCocM, Testul Cochran pentru studiul stabilitatii in functionare a

masinilor unelte]

1 INPUT

2 SN←0,sm←0

3 INPUT

4 For i=1,2,..,k

4.1 INPUT

4.2

4.3 For j=1,2,..,n

4.3.1

4.4 For j=1,2,..,n

4.4.1

4.5

4.6

4.7 if then

4.7.1

4.8 if

Then

4.8.1

4.9 continue

5

6 if

Then

6.1 output

Else

6.2 output

7 STOP

3 Algoritm pentru verificarea normalitatii pentru e antioane de volum mic

Decizii Massey

Se verific[ normalitatea pentru e]antioane cu volum mic de selecie n, 10 n

Testul lui Massey const[ din urm[toarele: fie n, valorile de observaie x₁,x₂,.,x_n, a nivelul erorii de prima spe[ unde d₀ este dedcizia ca x urmeaz[ o repartiie normal[ fa[ de decizia d₁ ca x nu este repartizata normal. 

0 START [TM]

1 INPUT

2 INPUT

3 x ← 0

4 FOR i = 1,2,.,n

4.1

5

6 FOR i = 1,2, ..,n

6.1 k ← 1

6.3 FOR j = i, i + 1,. n

6.3.1 IF x_i < x_j

Then

.1 k ← j

6.3.2 CONTINUE

6.4 z ← x_i

6.5 x_i ← x_k

6.6 x_k ← x

7 S ← 0

8 FOR i = 1,2,..,n

8.1 S ← S + ( - x_i )

9 S ←

10 FOR I = 1,2,.., n

10.1 y_i ← (x_i - )/ S

11 f₁ ← 1/n

12 h ← f₁

13 FOR i = 1,2,.N

13.1 f_i ← f_i-1 +h

14 FOR i = 1,2,..n

14.1

15

16 FOR i = 1,2,.,n

16.1 IF dg < di

Then

.1. e ← i

16.2 CONTINUE

17 IF de < dg

Then

17.1 OUTPUT

Else

17.2 OUTPUT

18 STOP

Pentru riscul =0,05 valoarea lui dg se alege din tabelul

Pentru studierea durabilitatii (in minute) a unui tip de scule aschietoare trebuie verificate mai intai daca datele de selectie au o repartitie normala. Reproducem datele de selectie din /1/ .

5,05; 6,50; 7,16; 7,20; 9,40; 11,34; 12,18; 14,26; 16,10; 16,30; 17,54; 18,02; 21,28; 23,06; 24,58; 30,44; n = 16, d max = 0,1, dg = 0,126;

Se trage concluzia ca masuratorile au o repartitie normala

IV Studiul statistic al stabilitatii unui sistem analitic

O problema fundamentala pentru orice determinare analitica este aceea a stabilitatii parametrilor functiilor de transfer E = f(c).

Un sistem analitic reprezinta un model fizic realizabil, al unui ansamblu de fenomene existente, la care un grup de marimi ce le cauzeaza determina un alt grup de marimi reprezentand fenomenele.Fie sistemul:

E = f (c )

- c = marimea cauza (concentratia)

- E = efectul (semnale analitice)

instabilitatea unui sistem analitic ar determina aparitia intr-o serie de date experimentale a valorilor extreme, a fluctuatiilor periodice a discontinuitatilor

Corelarea seriala

Fie seria de date E₁, E₂,.E_n, corelarea seriala este corelarea intre perechile Ei si Ei+h, unde h este decalajul intre cele doua date experimente ce formeaza perechea, pentru i+h n se ia E_i+h = E_i+h-n (corelarea circulara).

Se calculeaza variabila de stabilitate (coeficientul de corelare seriala

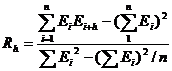
START [ CORER< Algoritm de calcul a coef.de corelare seriala]

INPUT

FOR h = 1,2,.,n-1

SM ←0

SP ← 0

SR ← 0

FOR I =1,2,.,n

2.4.1 SM ← SM +Ei2

2.4.2 SP ← SP + Ei

2.4.3 IF - i + h > n

THEN

.1 SR ← SR +Ei . Ei+h-n

ELSE

. .2 SR ← SR + Ei . Ei +h

2.4.4 CONTINUE

2.5

2.6 output

2.7

2.8

2.9

2.10 if R1(0.975) <R1<R1(0,025)

Then

.1 output

.2 stop

2.11 if R1(0,975)>R1>R1(0,955) sau R1(0,25)<R1<R1(0,005)

Then

.1 output

.2 stop

2.11 if R1(exp)<R1(0,995) sau R1(exp)>R1(0,005)

Then

.1 output

2.13 STOP

Testul secvential bayesian pentru controlul calitatii productiei

Se considera un process de productie de serie mare cu un procent de produse care prezinta defecte. Cu ajutorul testului secvential ne propunem sa adoptam una din deciziile:

d₁ : p = p0 ;

d₂ :p = p1 > p0 ;

d₃ : continua experimental

Consideram variabila x_i care poate lua valoarea 1 sau 0 dupa cum produsul i controlat prezinta sau nu defecte.

Algoritmul " CONTROL" permite rezolvarea unei probleme de decizie secventiala cu structura statistica a observatiilor binomiala utilizata in controlul calitatii produselor fabricate in serie mare. Semnificatiile variabilelor de intrare utilizate

- eroarea de prima speta

- eroarea de speta a doua

p₀ - proportia de piese defecte initiala

p₁ - proportia de piese defecte mai mare decat p0

0 START [ CONTROL]

1 INPUT

2 a ← pn (p1(1 - p₀) / (p₀(1 -p₁)))

3 b ← ln (l - p₀) /(l-p₁)

4 c ← ln ((l-p₀)/ )

5 d ← ln ( /(l- )

6 w ← 0; n ←1; SN ← 0

7 WHILE w = 0

7.1 INPUT

7.2 SN ← SN + XN

7.3 IF SN*a > c + n* b

THEN

7.3.1 OUTPUT

7.3.2. w ← 1

Else

7.3.3 IF SN*a < d + nb

THEN

.1 OUTPUT

.2 w ← 2

Else

.3 n ← n +1

7.3.4 CONTINUE

7.4 CONTINUE

8 STOP

Algoritmi de analiza bayesiana

Conceptele traditionale utilizate in statistica (teoria estimatiei si verificarea ipotezelor statistice) au fost repuse in drepturi de teorii noi mai generale care isi au originea in notiunea de joc si de decizie. Teoriile noi nu inlocuiesc pe cele vechi, ci permit o mai buna intelegere a fundamentelor si se aplica mai usor si corect.

Pentru a da un suport intuitiv problemei studiate, vom expune de la inceput un exemplu care ne va permite sa introducem si principalele exemple.

Exemplul 1. O masina fabrica piese in serie de 500 din care un procent f sunt defecte. Acest procent nu este cunoscut dar se stie ca el poate sa ia 4 valori.

0,01 ; 0,05; 0,15 ; 0,25

Fiecare piesa defecta costa 3 lei. Uneori este posibil de a elimina complet rebutul procedand la un reglaj complet al masinii care costa 70 lei. Ce decizie este mai rationala sa se ia?

A alege dintre:

d₁ : a nu face nimic

d₂ : a efectua un reglaj

Introducem tabelul costurilor in diferite situatii

d₁ d₂

f₁ = 0,01 17 70

__________________

f₂ = 0,05 75 70

__________________

f₃ = 0,15 225 70

__________________

f₄ = 0,25 375 70

Trebuie adoptata o decizie in conditii de incertitudine (valoarea luata de f ).

a)      In absenta oricarei informatii asupra gradului de verosimilitate a fiecarei valori posibile a lui f, este posibil de a formula un criteriu satisfacator.

Daca se doreste sa limitam riscul maxim trebuie sa luam decizia d2 (decizie minimax sau de extrema prudenta

b)      Presupunem ca intreprinderea poate da ponderi diverselor procente care rezulta din analizele statistice effectuate intr-o perioada mare de timp. De exemplu:

f p(f)

_____________

0,01 0,7

0,05 0,1

0,15 0,1

0,25 0,1

_____________

Alegem decizia care minimizeaza media matematica a costului