Indicatorii tendintei centrale

Indicatorii tendintei centrale

Indicatorii tendintei centrale sunt utilizati in analiza statistica a fenomenelor de masa, reprezentand expresia sintetizarii intru-un singur nivel reprezentativ a ceea ce este esential, tipic si general in aparitia, manifestarea si dezvoltarea fenomenelor.

Principalii indicatori ai tendintei centrale sunt:

1. valoarea medie ();
2. valoarea mediana (M);
3. valoarea dominanta (D).

Aplicatie

Notele obtinute la examen de 5 studenti sunt urmatoarele: 10, 6, 7, 10, 4.

Pentru a analiza pe ansamblu situatia celor 5 studenti se calculeaza cei 3 indicatori:

media (nota medie) se determina ca raport intre suma notelor obtinute si numarul studentilor:

mediana (nota mediana) este valoarea care imparte studentii in doua parti egale: 50% se situeaza sub nota mediana, 50% se situeaza peste nota mediana; se determina ca valoare (nota) centrala, dupa aranjarea valorilor seriei in ordine crescatoare sau descrescatoare.

valori in ordine crescatoare:

4, 6, 7, 10, 10

M = (50% dintre studenti au luat note sub 7,5% peste 7)

dominanta (nota dominanta) este nota care se inregistreaza la cei mai multi studenti:

D (pentru ca aceasta nota apare la un numar de 2 studenti, in timp ce notele celelalte apar la un singur student).

Ca urmare s-au calculat cei 3 indicatori ai tendintei centrale, care caracterizeaza seria statistica respectiva:

= 7,4

M

D =

Valorile acestora sunt diferite, urmare a faptului ca si continutul si semnificatia indicatorilor difera.

Mediile

Principalele caracteristici ale mediilor:

Mediile sunt indicatorii statistici cu cel mai mare grad de aplicabilitate practica.

Mediile se prezinta ca marimi cu caracter abstract, in sensul ca valoarea medie - de cele mai multe ori - nu coincide cu niciuna dintre valorile individuale din care s-a calculat (in exemplul anterior, niciunul dintre studenti nu a luat nota 7,4).

Media este nivelul la care ar fi ajuns caracteristica inregistrata, daca in toate cazurile, toti factorii esentiali si neesentiali ar fi actionat constant.

Pentru a asigura un continut real mediilor calculate, valorile individuale din care se obtin trebuie sa fie cat mai apropiate, sa existe o omogenitate a colectivitatii. In cazul eterogenitatii colectivitatii, aceasta trebuie separata pe grupe calitative pentru care se calculeaza medii partiale.

In analiza statistica se calculeaza mai multe tipuri de medii:

media aritmetica;

media armonica;

media patratica;

media geometrica;

media cronologica.

In practica, marimile medii nu se folosesc la intamplare, ci in functie de specificul si de proprietatile fenomenului respectiv se utilizeaza una sau alta dintre medii.

In continuare se prezinta detaliat media aritmetica, urmand ca si celelalte tipuri de medii sa fie tratata la temele urmatoare.

Media aritmetica ()

Media aritmetica este rezultatul sintetizarii intr-o singura expresie numerica a tuturor nivelurilor individuale observate si se calculeaza prin raportarea valorii totalizate a caracteristicii la numarul total al unitatilor.

Formula de calcul

A.      pentru seriile simple, adica in cazul in care numarul variantelor caracteristicii studiate este egal cu numarul unitatilor.

fie caracteristica X cu valorile X₁, X₂ ,, X_n, in care :

X₁+X₂++X_n = , unde n = numarul unitatilor

inlocuind fiecare valoare X_i cu se obtine:

,

de n ori

,

rezulta formula de calcul pentru media aritmetica simpla:

Aplicatie

Pentru cei 10 angajati ai unei firme s-au inregistrat in luna septembrie 2006 urmatoarele salarii lunare brute (in unitati monetare -u.m.):

Sa se calculeze salariul mediu lunar la nivelul firmei.

La nivelul firmei, salariile au variat intre 700 u.m. si 1100 u.m., iar salariul mediu a fost de 880 u.m.

B. pentru seriile cu distributie de frecvente, adica in cazul in care variantele caracteristicii se inregistreaza de mai multe ori (in exemplul anterior acelasi salariu este inregistrat la mai multi salariati: 900 u.m. la 3 salariati, 1000 u. m., 800 u.m. si 700 u.m. la cate 2 salariati, 1100 u.m. la 1 salariat.

formula de calcul pentru media aritmetica ponderata este urmatoarea:

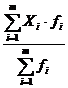
unde:

f_i = frecventa absoluta inregistrata la valoarea X_i a caracteristici

frecventa relativa (ponderea) inregistrata la valoarea X_i a caracteristicii.

m = numarul de grupe ale caracteristicii X.

Aplicatie

Pentru cei 10 angajati ai firmei (din aplicatia anterioara) salariile lunare brute inregistrate in luna septembrie 2006 sunt urmatoarele:

Salariul mediu se poate calcula in 2 moduri:

a.        pe baza frecventelor absolute

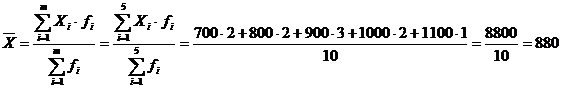u.m

b.       pe baza frecventelor relative

u.m

In unele cazuri variabila X_i nu este definita printr-un set de valori (de exemplu salariul de 700, 800, 900, 1000, 1100 u.m.), ci printr-un set de intervale egale (sau inegale) de grupare, de exemplu:

Aceasta situatie este intalnita, de regula, atunci cand numarul unitatilor de observare este foarte mare si, in plus, nu sunt cunoscute valorile individuale, ci numai incadrarea lor intr-un anumit interval.

Calculul mediei aritmetice ponderate se efectueaza pe baza acelorasi relatii. Deoarece fiecare grupa nu este caracterizata de o anumita valoare X_i a caracteristicii, ci de un interval, prin conventie se stabileste ca valoarea corespunzatoare fiecarui interval sa fie centrul intervalului de grupare (media aritmetica simpla a limitei inferioare si limitei superioare a intervalului).

Aplicatie

Pentru o firma cu 200 de angajati se cunosc urmatoarele informatii privind salariul brut realizat in luna septembrie 2006:

Nota: Limita superioara inclusa in interval.

Pentru intervalele inchise se stabileste centrul intervalului

Centrul intervalului de grupare este considerat a fi valoarea care exprima sintetic fiecare interval si corespunde ipotezei ca frecventele se distribuie uniform in cadrul fiecarui interval.

Pentru intervalele deschise se asigura, mai intai inchiderea acestora, considerand - in mod conventional - ca au aceiasi marime cu intervalele alaturate.

< 700 intervalul 600 - 700

1100 intervalul 1100 - 1200

In continuare media se poate calcula in 2 moduri:

a.        pe baza frecventelor absolute

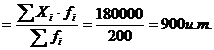
b.       pe baza frecventelor relative

Se observa din tabelul anterior ca frecventele relative au fost calculate in procente:

Pentru a calcula media, frecventele relative trebuie transformate sub forma de coeficienti, prin impartire la 100

Principalele proprietati ale mediei aritmetice

Media aritmetica are intotdeauna o valoare cuprinsa intre valorile extreme ale seriei:

<<

Daca media se plaseaza in afara acestor limite, rezultatul este in mod sigur eronat (control logic).

In cazul unei serii cu distributii de frecvente, media aritmetica se incadreaza intre valorile extreme ale variabilei si oscileaza in jurul termenului (intervalului) cu frecventa maxima.

In cazul aplicatiei anterioare:

<<

si in plus oscileaza in jurul intervalului (800-900) care are cea mai mare frecventa de aparitie (60 de salariati, respectiv 30% din total).

Suma abaterilor nivelurilor individuale de la media lor este egala cu 0.

pentru o serie simpla:

pentru o serie cu distributie de frecvente:

Aceasta proprietate se verifica foarte usor in cazul aplicatiilor prezentate.

Dezavantajul mediei aritmetice

Media aritmetica este sensibila fata de valorile extreme, astfel ca devine nereprezentativa daca termenii seriei sunt prea imprastiati.

Aplicatie

Pentru cei 10 angajati ai unei firme s-au inregistrat in luna septembrie 2006 urmatoarele salarii brute (in u.m.):

500; 500; 600; 600; 600; 600; 700; 700; 1800; 2000

Calculand salariul mediu lunar se obtine:

Fara a fi necesare calcule suplimentare^*) se observa ca media nu este reprezentativa. Colectivitatea de baza este alcatuita din 2 subcolectivitati total diferite: 8 angajati au un salariu 700 u.m. in timp ce 2 angajati incaseaza lunar 1800 respectiv 2000 u.m..

Ca urmare, salariul mediu calculat de 860 u.m nu sintetizeaza ceea ce este esential, tipic, pentru colectivitate.

Vezi coeficientul de variatie.

In consecinta, salariul mediu trebuie studiat separat pentru cele 2 tipuri calitative:

pentru cei 8 angajati cu salarii mici.

pentru cei 2 angajati cu salarii mari:

Astfel s-au calculat 2 salarii medii reprezentative, corespunzatoare celor 2 tipuri calitative.

Cele 2 medii partiale pot fi agregate in continuare, obtinand salariul mediu la nivelul firmei:

dar, subliniem inca o data, calculul are o valoare pur teoretica, salariul mediu - in aceasta situatie - fiind un indicator lipsit de continut.

Concluzie

Indiferent de media utilizata si de modelul de calcul, pentru verificarea gradului de reprezentativitate a acesteia este necesar sa se calculeze indicatorii variatiei si asimetriei.