OBIECTUL STATISTICII

1.1. Obiectul statisticii si importanta acestuia in economie

Statistica este stiinta care se ocupa cu descrierea si analiza numerica a fenomenelor de masa, dezvaluind particularitatile lor de volum, structura, dinamica, conexiune, precum si regularitatile sau legile ce le guverneaza [Trebici, V., 1985].

Exista un mare numar de definitii ale statisticii fapt care are mai multe explicatii; istorice - statistica s-a constituit la confluenta mai multor orientari si discipline, dar avand la origine un caracter social; metodologice - statistica incorporeaza o serie de metode in care predomina cele cantitative, cu fundamentarea epistemologica corespunzatoare; aplicative - prin generalitatea metodelor sale, statistica se aplica in cele mai variate domenii, de la astronomie la societate, de la microcosmos la macrocosmos in natura si societate, de la fizica statistica pana la statistica sociala.Trebici, V., 1985.

O definitie sau alta, staruie fie asupra unei faze din demersul metodologic, fie asupra unui domeniu restrans, fie asupra unui grup de metode, asupra teoriei sau dimpotriva a aplicatiilor.

In prezent statistica dispune de un corp de metode a caror putere de cunoastere este verificata in variate domenii si de o teorie generala in continua dezvoltare. Cultura statisticii devine tot mai mult o componenta din cultura generala a omenirii contemporane, iar gandirea statisticii - o modalitate stiintifica indispensabila pentru analiza si interpretarea unor clase foarte largi de fenomene.

Rezultat al unui indelungat proces, statistica se prezinta cu un corp comun de notiuni organizat in jurul conceptului de probabilitate, de metode stiintifice, cu fundamentare epistemologica explicita si cu o varietate de domenii de aplicare, acoperind practic natura si societatea.

Astazi, statistica constituie un puternic instrument de cunoastere a lumii inconjuratoare. Marea majoritate a disciplinelor imprumuta de la statistica modelele si procedeele acesteia, indispensabile de altfel indeplinirii rolului acestora. Trebuie mentionat insa marele pericol la care aceste discipline pot fi supuse in cazul folosirii necorespunzatoare a metodelor si procedeelor statistice.

Analiza si cunoasterea fenomenelor si proceselor social economice se poate realiza numai ca urmare a unei observari riguroase si metodice, in cursul careia ele pot fi masurate. In cadrul operatiei de modelare a fenomenelor si proceselor are loc un proces de simbolizare si abstractizare a lor in vederea analizarii sub aspect cantitativ. Analiza cantitativa constitute o faza premergatoare analizei calitative. Testarea modelelor construite se realizeaza prin intermediul operatiei de simulare. Pe parcursul tuturor fazelor de construire si testare a modelelor, statistica este mereu prezenta in campul cercetarii stiintifice fiind solicitata de a lua decizii pe baza metodelor si procedeelor pe care le pune la dispozitie. Modelul construit si testat vine in ajutorul statisticii sa aprofundeze cunoasterea fenomenelor si proceselor.

Modelarea matematica a castigat tot mai mult teren, dobandind o importanta deosebita, odata cu intensificarea aplicarii modelelor statistice. Culegerea si organizarea datelor rezultate din observari statistice constituie etapa premergatoare elaborarii unui model. In acest mod, modelul realizat va reprezenta o macheta a realitatii, alcatuita pe baza datelor din observarea statistica. Pe buna dreptate, modelarea este considerate o modalitate de cunoastere a realitatii inconjuratoare.

Organizarea culegerii, transmiterii si receptionarii informatiilor in cadrul unui sistem economic constituie obiectivele esentiale ale unui sistem informational. Un sistem informational este alcatuit din mai multe circuite informationale, unde fiecare in parte trebuie sa includa operatii de culegere, transmitere neperturbata a datelor si receptionarii acestora in scopul folosirii lor. Trecerea de la prelucrarea manuala la cea automatizata a tuturor fazelor din cadrul sistemului informational, adanceste procesul de cunoastere a realitatii, permitand asimilarea sistemului informational unui flux tennologic informational, prin transformarea lui intr-un sistem cibernetic. Organizarea circulatiei informatiei intr-un sistem in conformitate cu principiile sistemelor cibernetice, constituie un suport stiintific in abordarea gestiunii eficiente a acestuia. Avand in vedere natura nedeterminista a majoritatii elementelor componente dintr-un sistem cibernetic, studierea stabilitatii acestora se realizeaza apeland tot la statistica. Studii de reglare si echilibru intr-un sistem cibernetic se pot aborda numai pe baza unor observari statistice realizate metodic care ne permit sa construim modelul matematic in conformitate cu realitatea.

Informatica, prin aparatul sau, se implica tot mai mult in toate fazele de vehiculare si prelucrare a informatiilor din cadrul sistemelor informationale, conducand in acest mod la un salt calitativ important, cu consecinte semnificative si asupra statisticii. Calculatoarele electronice, prin puterea lor de calcul, conduc la o noua viziune cu privire la functiile statistice, precum si la modalitatile de realizare a acestor functii.

Realizarea automata si in regim interactiv a tuturor metodelor si procedeelor algoritmizabile din statistica, cu ajutorul calculatorului nu afecteaza cu nimic obiectul si metoda statisticii. Calculatorul electronic nu constituie decat un instrument de calcul, degajand statistica de volumul mare de calcule. In aplicatiile practice implementate cu ajutorul calculatorului specialistul este absolvit in totalitate de manipularea datelor cat si a operatiilor cu acestea, concentrandu-se in exclusivitate asupra interpretarii rezultatelor intermediare si finale.

Statistica informationala, care a fost denumita asa de academicianul Octav Onicescu, si-a gasit aplicatii practice in diverse domenii. Studierea sistemelor in raport cu informatia continuta in acestea, a permis o abordare sistemica si mai bine fundamentata matematic a realitatii. Teoria matematica a informatiei formuleaza legile cele mai generale cu privire la comenzile, controlul si comunicatiile dintr-un sistem, stabilind in acelasi timp principiile de codificare, prelucrare, pastrare si transmitere a informatiei de care statistica beneficiaza din plin. Initiatorul teoriei matematice a informatiei a fost Claude Shannon, care s-a bazat pe teoria probabilitatilor. Teoria initiata de Shannon a permis reducerea perturbatiei care influenteaza transmiterea informatiei.

Fiind un proces complex de cunoastere, judecata si actiune, managementul se concretizeaza prin operatii de informare, analiza si control, punctul esential constituindu-l momentul luarii deciziei. Toate aceste operatii folosesc metodele si procedeele statisticii incepand cu culegerea (observarea) datelor si incheind cu deducerea concluziilor necesare luarii deciziilor. Aceasta a permis conturarea unei discipline denumita teoria deciziei, avand drept scop fundamentarea stiintifica a procesului decizional. Deoarece teoria deciziei face apel si la modele deterministe, aceasta se integreaza intr-un domeniu mai larg privind matematica aplicata si anume in cercetarea operationala. Cercetarea operationala este considerata un instrument de conducere nationala a proceselor si fenomenelor cu un inalt grad de complexitate. Aceasta disciplina integreaza in cuprinsul sau metode si procedee statistice cat si o multime de tehnici de natura stiintifica, tehnica si de culegere si prelucrare a informatiei.

Decizii in situatii de risc constituie un alt domeniu in care statistica se aplica. Diversele variante de dezvoltare a unui fenomen sau proces, fie social sau economic, presupune descompunerea acestuia intr-o multime de evenimente care formeaza un camp complet de evenimente. Anticiparea celei mai plauzibile variante de dezvoltare a fenomenului presupune cunoasterea distributiei de probabilitate asociata acestuia. Acest lucru nu este posibil fara o observare metodica a evolutiei fenomenului in timp si ca urmare o determinare a legii de probabilitate pe care o urmeaza.

Aflarea distributiei de probabilitate, utilizand modele si procedee statistice, permite a aprecia gradul de risc la care este supusa o actiune sau alta.

In marketing statistica se regaseste in S.S.D.M. (sistemul suport al deciziilor de marketing), ca acesta fiind compus din ,,Banca statistica' si ,,Banca de modele'. SSDM este un ansamblu coordonat de date, sisteme, instrumente si tehnici, inzestrat cu tehnologia necesara ce ajuta o organizatie sa culeaga si sa interpreteze informatiile relevante referitoare la activitatea sa si la mediul in care opereaza facand din acesta temelia actiunilor de marketing. [Kotler.Pk, 1997}.

Pe baza celor prezentate se poate sublinia inca o data rolul si importanta cunoasterii metodelor si procedeelor puse la dispozitie de statistica in procesul cunoasterii. Nu este lipsit de importanta aportul statisticii nici in domenii ca: medicina, biologie, fizica, chimie, stiinte juridice etc. Frecvente sunt cazurile in care studii intreprinse in aceste domenii trag concluzii care au la baza o multime de date rezultate in urma unor observari statistice, implicand nemijlocit modele ale inferentei statistice.

Ronald Fisher a remarcat: ,,Catre statisticieni ne indreptam pentru a raspunde la problemele cele mai serioase puse de marile aventuri ale epocii noastre. De fiecare data cand se intreprinde ceva important, statisticienii sunt in culise. In toate cercetarile stiintifice de baza, ei sunt cei care elaboreaza planurile de experiena sau observatii si tot la ei se recurge pentru a analiza rezultatele pentru a evalua constatarile si pentru a separa faptele clar demonstrate de cele ce mai cer confirmarea' [Trebici, V., 1985.

Cercetarile stiintifice simt necesitatea unei ,,escorte statistice' in doua momente fundamental ale cercetarii: momentul de inceput legat de culegerea si prelucrarea datelor si in momentul aplicativ, de verificare a teoriilor pe calea confruntarii cu realitatea.

Multitudinea de domenii in care statistica se aplica i-a permis lui M.G. Kendall sa spuna ca ,,Statistica, in sensul cel mai larg, este matricea oricarei stiinte experimentale'.

1.2. Istoricul statisticii

Statistica, in contextul celorlalte stiinte, s-a confruntat ca discipline de sine statatoare, urmand o traiectorie care leaga practica de teorie. Preocupari de natura statistica, prin abordari variate a diverselor fenomene, se pierd in vechimea istoriei. Atat in Grecia antica, dar mai cu seama in imperiul roman, investigatiile arheologice au scos la iveala o serie de date care privescinventarierea bunurilor, a resurselor umane, descrierea geografica si politica a diverselor state.

Toate aceste preocupari, indiferent de natura lor, au constituit o consecinta a necesitatii practice, executandu-se in mod empiric si fara respectarea unor criterii riguroase. Beneficiari ai acestor date erau organele fiscale, militare si cele administrative, direct interesate in evaluarea potentialului uman si material a diverselor forme de organizare teritoriala sau statala. Aceste date serveau in principal nevoilor practice de orientare.

Interesele de ordin stiintific nu au intarziat prea mult sa apara, obligand statistica sa paraseasca stadiul de statistica practica. Incepea sa se impuna cunoasterea unor fenomene, referitor la care se cereau o multitudine de date. Ca urmare, apare necesitatea cunoasterii unor tehnici care sa permita desprinderea unor concluzii fundamentale pe baza datelor inregistrate. In faza incipienta de confruntare a statisticii, aceasta se marginea la descrierea statului, expunerea situatiei geografice, economice si politice. Acest mod de abordare a statisticii cunoscut sub numele de ,,descrierea statului' a predominat pana in sec. al 17-lea si al 18-lea cand a atins punctul culminant, concordand cu constituirea a in Germania a unei scoli, cunoscuta sub denumirea de scoala descriptiva germana.

In conformitate cu normele teoretice, care erau specifice universitatilor germane, descrierea statului s-a conturat ca o disciplina cu obiect propriu de predare. Ulterior, aceasta disciplina nascuta din practica a primit numele de statistica, devenind un obiect de studiu favorit in Germania. Termenul de statistica definit in spiritul scolii din Gottingen, a fost preluat de multi statisticieni recunoscuti ai epocii respective.

Reprezentantii scolii de statistica din Germania, s-au ridicat in oarecare masura peste orientarea pur descriptiva a inaintasilor, studiile care aveau drept obiectiv, descrierea statului inregistrand o noua dimensiune si anume cea numerica. In acest nou context, de imbogatire prin componenta numerica, statistica nu s-a schimbat din punct de vedere a continutului, ea continuand sa ramana o discipline orientata cu preponderenta spre descrierea fenomenelor si nu spre cautarea unor legi, ramanand o disciplina caracterizata de un mod de prezentare preponderent verbal. In acest context au fost elaborate lucrari cu privire la descrierea statelor in diferite tari europene, constituind astazi valoroase surse de informatie.

In Moldova, cea mai de seama lucrare este ,Descrierea Moldovei' a lui Dimitrie Cantemir. Aceasta lucrare, cu un pronuntat caracter monografic in plan geografic, politic, social si cultural, s-a impus in mod deosebit lumii europene din acea perioada, desemnandu-l pe autor in randul fruntasilor statisticii descriptive europene.

In perioada de avant a statisticii descriptive a statului, in Anglia si in afara universitatilor, apare un curent statistic nou, cunoscut sub numele de aritmtlica politica. Noul curent din statistica se caracterizeaza prin analiza datelor de observatie prin procedee matematice, relevarea regularitatilor in fenomenele social-economice, formulari si incercari de previzionare a unor fenomene.

Implicarea aparatului matematic in descoperirea legitatilor care caracterizau fenomenele constituia un real progres, anticipand aparitia statisticii moderne.

Reprezentantii de seama a noului curent in statistica au insistat in mod deosebit prin lucrari in domeniul demografiei, deoarece vedeau in studiul populatiei izvorul bogatiei si puterii Angliei. Merita sa amintim in acest sens pe John Graunt, William Petty si Edmund Malley.

J. Graunt, analizand cu atentie registrele de nasteri si decese din Londra, a incercat sa gaseasca legitatile cresterii populatiei, a echilibrului numeric dintre sexe, a fertilitatii, mortii etc. Studiile lui Graunt relevau, pentru prima oara, preponderanta nasterilor masculine in raport cu nasterile feminine (107 baieti la 100 fete), calculand primele rate de mortalitate pe grupe de varsta, alcatuind si o rudimentara tabela de mortalitate.

W. Petty, prin lucrarile sale, foloseste estimarile cantitative in compararea potentialului uman si economic al diferitelor state.

E. Halley a fost un reprezentant de seama a scolii statistice din acea vreme din Anglia, abordand in lucrarile sale subiecte legate de estimarea populatiei catorva state, bazandu-se pe criterii ceva mai rationale decat cele adoptate anterior, cat si alcatuirea primei tabele complete de mortalitate.

La promovarea principiilor aritmeticii in investigarea fenomenelor economice s-au evidential in mod deosebit alti doi reprezentanti ai scolii engleze: Devanant si King. Ultimul s-a dedicat in mod special calculelor privind veniturile statului pe calea impozitelor, de asemenea incercand sa stabileasca marimea capitalurilor de care dispunea Anglia in sec. al 17-lea, pierderile suferite in urma razboaielor, incendiilor, epidemiilor.

Influenta aritmeticii politice engleze s-a facut simtita si in alte tari, conturandu-se un curent al aritmeticii politice europene. Aritmetica politics s-a impus in lupta cu scoala statisticii descriptive din Germania, prin intermediul lui J.P. Sussmlich. Lucrarile sale se remarca in special prin: cautarea explicatiei fenomenelor vietii umane si indicarea legilor ce le guverneaza, corelarea fenomenelor demografice si economice, examinarea fenomenelor in dinamica, identificarea regularitatilor in volumul de date rezultate din observatii etc.

In consecinta, se poate afirma ca la sfarsitu! sec. al 18-lea, in statistica se prefigurau doua curente: primul curent corespunzator caruia statistica era

inteleasa ca o descriere empirica si verbala a caracteristicilor statului (statistica descriptiva) si al doilea curent conform caruia statistica trebuie sa se dedice analizei fenomenelor sociale, in cautarea de legitati intemeiate cu regularitate pe observatii si calcule numerice (aritmetica politica).

Statistica, prin curentele sale, castiga teren tot mai mult, iar descrierile statistice devin preocupari de baza in institutiile publice. Aritmetica politica, sub aspect conceptual, capata o noua dimensiune odata cu inventarea calculului probabilitatilor. Aceasta noua ramura a matematicii, avea sa indeplineasca misiunea fundamentarii stiinfifice a preocuparilor statistice de pana atunci. Bernoulli si Laplace aveau sa fie primii care au utilizat modelele teoriei probabilitatilor in studiul statistic al fenomenelor economice si sociale. Bernoulli formuleaza ,,legea numerelor mari', deschizand drumul aplicarii calculului probabilitatilor in economie. Laplace s-a preocupat de studierea fenomenelor dependente de diversi factori complecsi de actiune, prefigurand utilitatea acestui calcul si in abordarea de ansamblu a fenomenelor sociale.

Un alt reprezentant de seama al calculului probabilitatilor a fost Gauss, care a definit legea de repartitie normala. In aceeasi perioada, Fourier a publicat un numar de studii'despre aplicarea matematicii in investigatii demografice, iar Poisson descopera legea de repartitie a evenimentelor rare.

Gandirea probabilistica avea sa se consolideze in statistica in secolul al 19-lea, asigurandu-i progresul si renumele de care se bucura astazi in intreaga lume. Un reprezentant de seama din aceasta perioada si care a dominat gandirea statistica a acestui secol a fost matematicianul, astronomul si statisticianul belgian Adolphe Quatelet. Conform teoriei acestui mare ganditor, diversele caractere fizice, intelectuale si morale ale oamenilor, observati in masa, s-ar echilibra intr-o fiinta fictiva, ideala, dorita de natura, dar neizbutita. Fiintele umane, conform teoriei ,,omului mediu', s-ar distribui de-o parte si de alia a acestei fiinte ideale. Pentru a desprinde ce este general fiintei umane, A. Quetelet presupune debarasarea omului de caracterele individuale ale sale care nu sunt decat accidentale. Ideea de ,,om mediu' a constituit izvorul de inspiratie privind o serie de notiuni si concepte noi din statistica, cum ar fi: repartitie, medie, dispersie, observare de masa, regularitate etc. In conformitate cu teoria iui A. Quetelet, regularitatile deduse ca urmare a unei observari de masa deriva din legi care sunt urmate de om atat in ordinea fizica cat si in cea morala. Lui A. Quetelet i se atribuie, pentru prima oara, o teorie sintetica a statisticii bazata pe principii, tehnici si procedee statistice. Acesta imprima statisticii noi directii de cercetare: cercetarea variatiei si a relatiilor cazuale in masa fenomenelor, sesizarea regularitatilor, abordarea cu prioritate a fenomenelor vietii umane etc. Conform teoriilor lui A. Quetelet, statistica defineste metode unice necesare studierii fenomenelor bazate pe calculul probabilitatilor, endinta de ansamblu, dedusa pe baza unui volum mare de observatii statistice. Legea statistica se poate pune in evidenta numai daca se considera un numar suficient de mare de unitati statistice elementare ale populatiei de studiat supuse observarii.

Legea numerelor mari, care constituie o expresie a legaturii dintre neccsitate si intamplare, se verifica in colectivitati relativ mari si cuprinzatoare. In conformitate cu aceasta lege, actiunea conjugata a unui numar mare de factori aleatori, in conditii bine determinate, conduce la rezultate aproape independent de intamplare, dand astfel posibilitatea ca necesitatea sa se realizeze. Referindu-ne la prima lege statistica descoperita stim ca la nastere numarul baietilor intrece pe eel al fetelor, raportul initial admis era de baieti 107; fete 100. Particularizand aceasta lege statistica la distributia pe sexe a nascutilor in sanul fiecarei familii in parte, ar fi imposibil sa indicam ce fel de raport exista, date fiind variabilele sale destul de numeroase si in acelasi limp importante pentru diferite familii. O cercetare statistica care sa prezinte rezultate semnificative in acest sens, trebuie intreprinsa pe mase indeajuns de mari de nasteri : insusi J. Bernoulli care a dat acestei legi o forma matematica, a tinut sa mentioneze la vremea sa, ca sporirea numarului observatiilor in scopul maririi gradului de siguranta a deciziei nu constituie ceva nou si neobisnuit, deoarece omul indiferent de pregatirea sa stie ca sursa de reusita referitor la o actiune a sa este cu atat mat mare, cu cat mai multe observatii sunt luate in considerare.

1.2.1. Scurt istoric privind evolutia statisticii in Romania

Despre un inceput de organizare statistica in tarile romanesti nu poate fi vorba decat din secolul al. XVIII-lea incoace. Prima scriere sau recensamant al locuitorilor pare sa fi fost facuta de Constantin Mavrocordat, cu ocazia reformelor sale in Muntenia si Moldova. Regulamentul organic (1831) introduce catagrafia sau recensamantul sistematic si periodic. Din 7 in 7 ani trebuia sa se faca categrafia populatiei, dupa norme bine stabilite, pentru a servi la ,,asezarea birului si la hotararea veniturilor tarii'.

La 28 aprilie 1859, domnitorul Al. I. Cuza aproba infiintarea unui birou de statistica in Tara Romaneasca, numind sef pe Dionisie Pop Marxian, iar la I iulie 1859 aproba infiintarea Directiei de Statistica din Moldova, sub conducerea lui Ion lonescu de la Brad.

La 4 august 1862 cele dou3 organe de statistica se reunesc sub denumirea Oficiului Statistic pentru Principatele Unite sub conducerea lui Dionisie Pop Martian.

Gandirea statistica romaneasca s-a aliniat in contextul amplu al curentelor statistice existente in Europa. Reprezentantii statisticii romainesti au pastrat un contact permanent cu preocuparile statistice din tarile Europei, aducandu-si contributia de seama atat la promovarea statisticii teoretice si practice, cat si al organizarii ei institutionale. Cei mai de seama reprezentati ai statisticii romanesti din acea perioada au fost Ion lonescu de la Brad si Dionisie Pop Martian. Primul si-a prezentat punctul de vedere despre statistica in lucrarea intitulata ,,Povaturi pentru catagrafia Moldovei' (1859). Statistica, in viziunea lui I. I. de la Brad trebuie sa cuprinda doua parti: o prima parte care sa presupuna culegerea datelor de observare, iar a doua parte sa implice aparatul matematic. Se regaseste in aceste abordari metodologice, in linii mari, insusi demersul statistic modern, format din doua etape: una descriptiva, alta inductiva, inferentiala..

In conceptia lui D. P. Marjian statistica trebuie sa studieze fenomenele naturale si sociale, avand drept scop descoperirea legilor care le guvemeaza. Se evidentiaza apartenenta sa la curentul de larga circulatie conform caruia obiectul de cercetare al statisticii trebuie sa depaseasca granitele sferei fenomenelor sociale.

In spiritul statisticii descriptive europene si la noi in tara s-au scris lucrari statistice, statistica figurand ca obiect de studiu in invatamantul romanesc. Un curs de statistica a fost introdus in 1856 la Facultatea Juridica de la Academia Mihaileana din lasi de catre Al. Papiu llarian, care avea drept obiect descrierea statelor componente ale Europei sub aspect economic si social.

In 1860 apar Analele Statistice pentru cunoasterea Romaniei, in care se publica lunar date privind statistica agricola, statistica vamilor, a miscarii populatiei precum si studii cu caracter economic.

In 1918 este creat Institutul Social Roman, forma institutionalizata de cercetare sociologica. Rezultatele au fost publicate sistematic in ,,Arhivele pentru stiinta si reforma sociala', aparand primele cercetari statistice sub forma de monografii. [Bogdan, V., 1995].

Un recensamant general al populatiei, cladirilor, intreprinderilor industriale si comerciale are loc in 1930. Debutul Anchetei Bugetelor de Familie are loc in 1950, care va deveni cercetare permanenta intre 1950-1994.

In 1964 are loc o reuniune stiinpfica cu tema ,,Anchetele selective', cand pentru prima data in Romania sunt formulate principle proiectarii si utilizarii unui esantion maitre .

1.3. Concepte de baza

1.3.1. Populatia statistica

Populatia statistica reprezinta multimea elementelor simple sau complexe, de aceeasi natura, care au una sau mai multe insusiri esentiale comune, proprii elementelor cat si populatiei privita ca un tot unitar. Florea I., 1998}

O populatie este finita daca include un numar determinat de elemente, dar ea poate fi considerate drept reprezentativa a unei populatii teoretice infinite. Ca urmare apare necesitatea de a delimita o populate in: continut, spatiu si timp. Se mai denumeste si populafia univers.

Exemple de populatii statistice: multimea persoanelor dintr-o anumita tara, localitate, zona etc. in anul t, multimea gospodariilor din Romania, la momentul t, multimea consumatorilor unui produs, multimea societatilor producatoare sau concurente ale unui produs, mullimea societatilor distribuitoare, angajatii unei societati, etc.

Se noteaza cu majusculele de la inceputul alfabetului: A, B, etc.

Unitatea statistica constituie elementul component, al populatiei statistice, asupra caruia se va efectua nemijlocit observarea.

Unitatea statistica este purtatorul originar de informatie sau subiectul logic al informatiei statistice. Datorita varietatii aspectelor sub care se poate prezenta in fapt, unitatea statistica comporta o definitie precisa, care sa excluda prin posibilitate de interpretare diferita de catre observatori si astfel orice eroare ce poate prejudicia valoarea investigatiei.

In exemplele citate mai sus, unitatile statistice sunt: persoana, gospodaria, consumatorul, societatea producatoare sau concurenta, societatea distribuitoare, angajatul etc.

Se noteaza cu minusculele corespunzatoare majusculei ce simbolizeaza populatia statistica, respectiv a_L, b, etc..

Volumul populatiei reprezinta numarul unitatilor statistice care alcatuiesc populatia statistica. Acesta poate fi finit sau infinit, in functie de tipul populatiei care poate fi la fel finita sau infinita.

Se noteaza cu N, iar pentru o populate A, avem: A :

- frecventa de cumparare: variabila atributiva calitativa

Y =

- numar de sortimente cumparate relativ la produsul analizat: variabila atributiva, cantitativa, discreta:

Z=

- localizarea magazinelor de unde cumpara: variabila de spatiu , calitativa

S=

- data ultimei cumparari a produsului analizat: variabila de timp,

T =

Variabila aleatoare

Variabila aleatoare este variabila care poate lua orice valoare din valorile unei multimi finite sau infinite, cu o anumita probabilitate, rezultata dintr-o functie asociata variabilei, numita lege de probabilitate.Ca si variabila statistica, variabila aleatoare in raport cu valorile sale poate fi discreta sau continua.

In timp ce o variabila aleatoare inregistreaza valori la intamplare, variabila statistica constituie o insusire certa a unitatilor statistice din populatie. Valorile unei variabile aleatoare sunt probabile si in stransa legatura cu un anumit experiment. Starile unei variabile statistice nu sunt probabile, ele cuantifica o trasatura proprie fiecarei unitati din populatie.

1.3.3. Observarea statistica

Observarea statistica consta in identificarea unitatilor populatiei si inregistrarea starilor variabilelor in raport cu care este studiata. Ansamblul starilor variabilelor rezultate prin observare se numesc statistici.

Dupa gradul de cuprindere a populatiei statistice, observarea statistica este de doua feluri: totala si partiala.

Observarea totala este acel tip de observare statistica in care are loc inregistrarea tuturor unitatilor care fac parte din populatie statistica supusa studiului. Recensamantul populatiei Romaniei este un exemplu de observare totala.

Observarea partiala presupune observarea si inregistrarea unui anumit numar de unitati din populatie, alese dupa criterii bine definite.

In cercetarea statistica a unei populatii punctul de pornire il poate constitui fie statistici exhaustive rezultate prin observarea populatiei univers , fie statisticile rezultate din observarea partiala a unui esantion A ≤A, in ambele cazuri scopul final fiind acelasi - obtinerea de informatii la nivelul populatiei univers A.

In primul caz, ansamblul de tehnici folosite in prelucrarea statisticilor se bazeaza pe matematica delerminista si au un caracter relativ simplu. Acest demers al cercetarii statistice constituie obiectul asa numitei statistici descriptive.

In al doilea caz tehnicile cantitative utilizate se bazeaza pe teoria probabilitatilor, permitand extinderea informatiilor de la esantion la populatia univers - inductie statistica. Acest demers constituie obiectul asa numitei statistici inferentiale.

1.3.4. Seria statistica

Seria statistica este o constructie care reda fie distributia unei populatii in raport cu una sau mai multe variabile, fie variatia unei marimi in timp, in spatiu sau de la o categorie la alta.

Seriile statistice se clasifica in raport cu mai multe criterii, astfel:

1. In raport cu numarul variabilelor

Serii statistice unidimensionale, au la baza o singura variabila;

Serii statistice multidimensionale, care au la baza doua sau mai multe variabile.

2. Dupa natura variabilelor deosebim:

Serii aiributive, care au la baza variabile atributive;

Serii cronologice (de timp sau istorice), care au la baza variabile de timp;

Serii de spatiu sau teritoriale, care au la baza o variabila de spatiu.

3. Dupa modul de exprimare a starilor variabilei deosebim:

Serii calitative, care au la baza variabile calitative;

Serii cantitative, care au la baza variabile cantitative si care dupa modul de variatie a variabilei pot fi: discrete (cand variabila este discrete) si continue (cand variabila este continua).

4. In raport cu natura indicatomlui din care este alcatuita seria, avem:

Serii de frecventa sau serii de distributie (repartitie);

Serii de variatie.

Seria statistica redand distributia populatiei in raport cu una sau mai multe variabile constituie o descompunere a acesteia intr-un numar R de clase. O astfel de serie este formata in exclusivitate din frecvente (absolute cumulate sau necumulate, relative cumulate sau necumulate) si de aceea se numesc serie de frecventa, de distributie sau de repartitie. Prescurtat se mai foloseste si denumirea de repartitie statistica sau distributie statistica.

Seria statistica ce reda variaria unei marimi in timp, in spatiu sau de la o categorie la alta se numeste serie de variatie.

1.3.4.1. Seria statistica de repartitie

Conform definitiei de mai sus, prin aceasta serie se distribuie unitatile

unei populatii statistice in raport cu una sau mai multe variabile.

Fie o serie statistica unidimensionala avand la baza variabila X,

respectiv:

X:

N_i este frecventa absoluta a clasei i, i= si reprezinta numarul de unitati ale populatiei din clasa pentru care variabila X a inregistrat valoarea X_i ;

N₁+N₂+.+N_R = N

Clasa (grupa) de unitati in raport cu o variabila reuneste acele unitati din cadrul populatiei care inregistreaza aceeasi stare a variabilei sau starile variabilei apartinand unui anumit interval de variatie.

Ca urmare, in raport cu o variabila statistica populatia poate fi structurata intr-un anumit numar de clase.

Exemplu

Fie A - populatia statistica reprezentand unitatile de cazare turistica din Romania, in anul 1999 si X - categoria de confort (este o variabila statistica atributiva, cantitativa discreta). Distributia acestor unitati in raport cu variabila X este urmatoarea (conform A.S. al Romaniei, 2000)

X:

0 - neclasificate;

1090 - ne arata numarul unitatilor de cazare turistice avand categoria de ,,2 stele';

De asemenea, relativ la seria statistica unidimensionala avand la baza variabila X, poate fi formata cu frecvente relative, frecvente cumulate absolute sau relative.

Fie seria X formata cu frecvente relative:

X: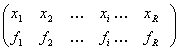

f_i - ne arata ponderea unitatilor din populatie care au inregistrat pentru variabila X starea x_i:

f_{i =} sau

f_{i =} i = = 1 (100%)

Exemplu:

X:

Sau:

X:

33,55 % reprezinta ponderea unitatilor de cazare turistica avand categoria de ,,2 stele'.

Pornind de la seria (1.1) se poate deduce seria formata cu frecvente absolute cumulate, respectiv:

X : 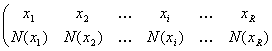(1.3.)

unde: N(x_i) reprezinta numarul de unitati din populatia studiata pentru care variabila inregistreaza valori ce nu depasesc valoarea x_i.

N(x₁) = N₁

N(x₂) = N₁+N₂

_..........

N(x_i) = N₁ + N₂ + +N_i

_{...............}

N(x_R) = N₁ + N₂ + +N_i + . + N_R = N

Exemplu.

X:

2864 - ne arata numarul unitatilor de cazare turistica avand cel mult doua stele.

Pornind de la seria (1.1) sau (1.2) se poate deduce seria formata cu frecvente relative cumulate, respectiv:

X 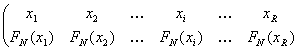(1.4.)

unde: f_N(x_i) - exprima ponderea unitatii populatiei studiate pentru care variabila a inregistrat valori ce nu depasesc valoarea x_i.

F_N(x_i) = f_{1 +} f_{2 +. +} f_i

F_N(x_i) = * 100 i =

Exemplu:

X:

88,15 % - reprezinta ponderea unitatilor de cazare turistice avand cel mult ,,2 stele'.

Asa cum se poate constata din definitia celor doua marimi de frecvente cumulate, acestea se pot calcula si are sens elaborarea unor serii statistice doar in cazul in care la baza seriei se gaseste o variabila cantitativa.

Relativ la aceeasi populatie statistica studiata A - multimea unitanlor de cazare turistica din Romania in anul 1999, din A.S. al Romaniei /2000, se pot extrage alte serii statistice de repartipe, ca de exemplu:

- distributia unitatilor de cazare in raport cu forma de proprietate (cf. A.S. al Romaniei/2000, pg.518).

Y :

Aceasta este o serie statistica de repartitie unidimensionala avand la baza o variabila atributiva, calitativa si formata cu frecvente absolute, in aceasta situatie se poate elabora seria statistica formata cu frecvente relative, respectiv:

Y :

distributia unitatilor de cazare in raport cu tipul destinatiei turistice (cf. A.S. al Romaniei/2000, pag.519)

Z

Este o serie statistica de repartitie unidimensionala avand la baza o variabila atributiva calitativa si formata cu frecvente absolute. Se poate elabora seria formata cu frecvente relative.

De asemenea, se pot elabora serii de repartitie unidimensionale in raport cu numarul de turisti cazati, cu gradul de utilizare a capacitatii in functiune, capacitatea existenta etc.

Seria statistica de repartitie bidimensionala este o constructie ce reda distributia unei populatii in raport cu doua variabile.

Astfel, fie populatia statistica A studiata in raport cu variabilele X si Y, rezultatele observarii se pot grupa intr-un tabel de forma urmatoare:

unde:

N_ij reprezinta numarul de unitati pentru care, variabila X inregistreaza starea Xj si variabila Y inregistreaza starea yi, ;

N_i numarul de unitati pentru care Y ⁼ y,, indiferent de nivelul inregistrat de variabila X;

N_j numarul de unitati pentru care X = Xj, indiferent de nivelul inregistrat de variabilaY;

- N - numarul total de unitati analizate.

Din seria bidimensionala se pot extrage serii unidimensionale de forma urmatoare :

X :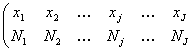

X :

denumite si serii de repartitie marginale, in raport cu X si Y

X/Y = y_j :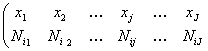

denumita seria de repartitie unidimensionala in raport cu X conditionata de Y = y_i, numarul acestora fiind egal cu numarul de stari a variabilei Y.

Y/ X = x_j :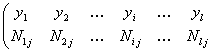

denumita serie de repartitie unidimensionala in raport cu Y conditionata de X = x_j, numarul acestora fiind egal cu numarul de stari a variabilei X.

De asemenea se poate elabora sau deduce seria de repartitie bidimensionala formata cu frecvente relative, respectiv:

f_{ij =} f_{j =} f_{i =} i =

Exemple:

Relativ la populatia statistica A studiata, din A. S. al Romaniei/2000, se poate extrage o serie de repartitie bidimensionala, avand la baza variabilele:

X - categoria de confort (numar de stele)

Y - tipul unitatii de cazare turistica de forma urmatoare:

Sursa: A.S. al Romaniei/2000, pag.515

21 - ne arata numarul de pensiuni agroturistice avand categoria de confort de 3 stele.

Tabelul de mai sus este o repartitie statistica bidimensionala avand la baza o variabila X atributiva cantitativa discreta si o variabila Y atributiva calitativa, formata cu frecvente absolute.

Se poate deduce seria de repartitie bidimensionala formata cu frecvente relative, respectiv:

0,6 % - reprezinta ponderea pensiunilor agroturistice avand categoria de confort de ,,3 stele', din totalul unitatilor de cazare turistica.

De asemenea se pot extrage seriile unidimensionale marginale in raport cu X si Y si cele conditionate, de exemplu:

X:

Y:

X/Y = pensiuni turistice :

Y/X = 3 :

1.3.4.2. Seria statistica de variatie

Conform definitiei seria de variatie reda variatia unei marimi, in timp, in spatiu sau de la o categorie la alta. Ca urmare, in continuare vom vorbi de serii cronologice (au la baza o variabila de timp), serii de spatiu si serii categoriale (au la baza variabile atributive). Cele mai des intalnite sunt seriile cronologice si seriile de spatiu.

Seriile de variatie au la baza marimi absolute si relative. Dupa unii autori din cadrul marimilor absolute fac parte indicatorii de nivel si diferenta absoluta a unei marimi, iar din cadrul marimilor relative fac parte: indicatorul relativ de intensitate, indicele statistic si diferenta relative a unei marimi.

Indicatorul de nivel (Y) este o marime ce reflecta nivelul unui fenomen analizat. De exemplu: productia diferitelor produse, veniturile populatiei, suprafata cultivata cu principalele culturi, transportul, exportul, importul etc.

Diferenta absoluta a unei marimi (Δy) exprima diferenta dintre nivelul cercetat si nivelul baza de comparatie al marimii analizate. Se exprima in aceeasi unitate de masura in care este cuantificat fenomenul analizat si ne arata cu cat s-a modificat acesta de la un nivel la altul.

Indicele statistic al unei marimi (/_y ) exprima raportul dintre nivelul cercetat si nivelul baza de comparatie al marimii analizate. Ne arata de cate ori se modifica acea marime, de la un nivel la altul.

Diferenta relativa a unei marimi (R_y) exprima raportul dintre diferenta absoluta a marimii respective si nivelul baza de comparatie al acesteia. Ne arata cu cat la suta se modifica marimea de la un nivel la altul.

Indicatorul relativ de intensitate (d) se defineste ca raport intre doi indicatori de nivel de natura diferita si arata gradul de raspandire a fenomenului cuantificat de indicatorul de la numarator in raport cu fenomeoul cuantificat de indicatorul de la numitor. De exemplu: productia diferitelor culturi / ha, densitatea populatiei, productia principalelor produse / locuitor, rata somajului etc.

Greutatea specifica (g) reflecta structura fenomenului analizat in raport cu starile variabile X, de la baza seriei.

Seriile cronologice

Seria cronologica reflecta evolutia in timp a unei marimi.

Valorile variabilei ca functie de timp pot fi fixate la un anumit moment de timp sau sa se refere la un interval de timp.

Seria cronologica de momente este o serie de observatii ordonate in timp, exprimand stocuri [Trebici V.. 1985]. De exemplu, volumul populatiei, numar de universitati, banci, institutii, fonduri fixe, numarul salariatilor, intreprinderile mici si mijlocii din diferite domenii de activitate, unitatile de cazare turistica etc.Intr-o astfel de serie insumarea marimii analizate nu are sens din punct de vedere al continutului, aceasta fiind permisa din considerente de calcul, ajustat etc.

Seria cronologica de intervale este o serie de observatii ordonate in timp exprimand fluxuri. De exemplu: nascutii vii, divorturile, decesele, productia diferitelor culturi sau produse, venituri, cheltuieli, productia industriala, agricola, exportul, importul etc.Intr-o astfel de serie are sens insumarea marimii analizate.

Fie o serie cronologica de momente sau de intervale ce reflecta evolutia in timp a nivelului unei marimi Y,

Y: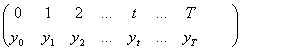

Pornind de la aceasta serie se pot deduce seriile formate cu diferente absolute, indici si diferente relative. In functie de modul de raportare a starilor variabilei timp t, marimile de mai sus se pot calcula cu baza fixa (t / to) (baza de comparatie ramane aceeasi) sau cu baza in lant(t /t-1) (baza de comparatie se schimba, fiind considerata cea precedenta nivelului comparat).

Fie seriile cronologice formate cu: - diferente absolute cu baza fixa:

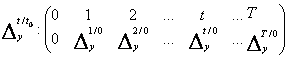
= y(t) - y(0)

diferente absolute cu baza in lant

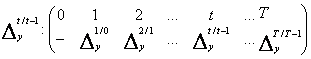
Intre cele doua tipuri de diferente absolute cu baza fixa si cu baza in lant, exista relatii de legatura ce ne permit exprimarea unora in functie celelalte. In acest context, insumand diferentele absolute cu baza in lant se obtin diferentele absolute cu baza fixa.

Scazand diferentele succesive cu baza fixa se obtin diferenfele cu baza in lant.

y(t) - y(0) - y(t-1) + y(0) = y(t) - y(t-1) =

Diferenta absoluta ne arata cu cat se modifica marimea analizata de la un moment la altul. Se exprima in aceeasi unitate de masura in care este cuantificat fenomenul studiat.

Daca fenomenul analizat se exprima valoric, atunci diferenta absoluta nu reflecta prea bine modificarile ce intervin, impunandu-se utilizarea marimilor relative respective, indicele statistic si diferenta relativa.

Fie seriile cronologice formate cu:

- indici statistici cu baza fixa

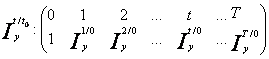
*100

- indici statistici cu baza in lant :

* 100

Indicele statistic ne arata de cate ori se modifica fenomenul analizat. Este marimea cel mai des folosita in caracterizarea evolutiei fenomenelor din economie.

Avand ca baza de referinta o serie cronologica de forma (1.7) se pot elabora serii formate cu:

- diferente relative cu baza fixa

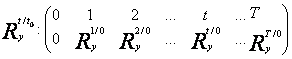
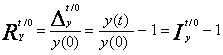
sau

diferente relative cu baza in lant

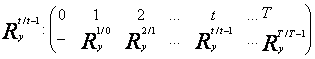(1.13)

Diferentarelativa ne arata cu cat la suta se modified fenomenul de la un moment la altul. Aceasta mSrime la fel ca si indicele statistice, se foloseste frecvent in caracterizarea fenomenelor din economic.

Daca seria cronologica analizata, de forma (1.7) este de intervale, se poate deduce seria formata cu greutatea specifica :

g _y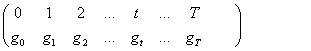

g(t) =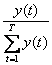

Seria statistica de spatiu (teritoriala)

Seria statistica de spatiu este o constructie statistica ce reflecta variatia in spatiu a unei marimi.

Seria de spatiu prezinta o importanta din ce in ce mai mare, datorita dezvoltarii sistemului informational, a necesitatii comparatiilor internationale si a comparatiilor intre regiunile unei tari.

In cadrul Anuarului Statistic al Romaniei exista capitole distincte de ,,Statistica teritoriala' si ,,Statistica internationala'. In capitolul de ,,Statistica teritoriala' sunt cuprinse informatii privind: populatia, fort a de munca, conditii de munca, veniturile populatiei, cheltuielile si consumul populatiei, locuinte, asistenta sociala, sanatate, invatamant, cultura, sport, conturi nationale, rezultate si performante ale intreprinderilor, agricultura, silvicultura, industrie, transporturi, posta, telecomunicatii, turism, finante, justitie si starea infractionala, pe cele 7 regiuni si Bucuresti.

La baza seriei de spatiu se gasesc atat marimi absolute (indicator de nivel, diferenta absoluta), cat si marimi relative (indicator relativ de intensitate, indicele statistic, diferenta relativa).

Fie seria statistica Z, de forma urmatoare:

Z: (1.15)

unde:    __

Si - este o stare a variabilei ce exprima spatiul,    i=1,R,

Z(i) - exprima o marime (indicator de nivel sau relativ de intensitate).

Plecand de la seria de forma (1.15) se pot deduce seriile formate cu:

- diferente absolute cu baza fixa:

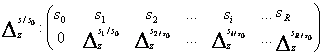
= z(i) - z(0)

- indicii statistici cu baza fixa

= * 100

diferente relative cu baza fixa

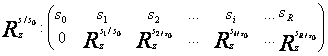
= * 100

Se deduc seriile formate cu marimi absolute si relative calculate doar cu baza fixa (se poate alege orice stare a variabile ce exprima spatiu).

PROBLEME PROPUSE (capitolul 1)

PI. Dati 5 exemple de populatii statistice a caror cercetare ar prezenta interes si pentru fiecare populatie selectata precizati:

1. denumirea populatiei, a unitatii statistice si volumul acesteia;

2. scopul cercetarii statistice;

3. variabilele statistice in raport cu care s-ar face observarea statistica a populatiei.

P2. Sa se extraga din Anuarul Statistic sau alte surse informationale o serie statistica bidimensionala ce reda distributia unei populatii in raport cu doua variabile atributive, relativ la care se cere:

1. denumirea populatiei ce a fost supusa observarii si volumul acesteia;

2. unitatea statistica;

3. caracterizarea variabilelor statistice in raport cu care a fost studiata populatia;

4. caracterizarea seriei statistice in raport cu toate criteriile cunoscute;

5. elaborarea seriei bidimensionale formata cu frecvente relative, interpretare;

6. extragerea repartitiilor unidimensionale marginale si a celor conditionate;

7. pornind de la o repartitie marginala deduceti celelalte serii statistice posibile, interpretare.

P3. Din Anuarul Statistic sau alte surse informationale extrageti o serie statistica de repartitie, avand la baza o variabila de spatiu, relativ la care se cere:

1. denumirea populatiei statistice si volumului ei;

2. unitatea statistica;

3. caracterizarea seriei dupa toate criteriile cunoscute;

4. deducerea seriei formata cu frecvente

5. interpretare.

P4. Din Anuarul Statistic sau alte surse informationale extrageti doua serii cronologice avand la baza indicatorul de nivel, una de momente, alta de intervale si deduceti seriile formate cu diferente absolute, indici statistici, diferente relative, cu baza fixa si cu baza in lant (interpretari).

P5. Dati 5 exemple de serii cronologice avand la baza indicatorul relativ de

intensitate.

P6. Din Anuarul Statistic sau alte surse informationale extrageti o serie de spatiu formata cu indicatorul de nivel sau indicator relativ de intensitate si deduceti seriile formate cu diferente absolute, indici si diferente relative, calculate cu baza fixa. Interpretare.

P7. Extrageti 5 exemple de serii de spatiu ce contin informatii importante pentru domeniul economic.

P8.Se da urmatoarea serie de variatie, cronologica, de momente, avand la baza un indicator de nivel :

-farmaciile din Romania la sfirsitul anului 1989

Z :

Deduceti seriile formate cu toti indicatorii derivati posibili.

P9.Se da urmatoarea serie de variatie, cronologica, de intervale, avand la baza un indicator de nivel :

Z :

Deduceti seriile formate cu toti indicatorii derivati posibili.

P.10 Se considera o firma a carei C.A. a evoluat in ultimele 12 luni dupa cum urmeaza :

-Luna 1-220

- Luna 2-225

- Luna 3-240

-Luna 4-250

- Luna 5-240

- Luna 6-245

- Luna 7-260

- Luna 8-280

- Luna 9-270

- Luna 10-275

- Luna 11-290

- Luna 11-290 (mil.lei)

Se cere :

1.Alcatuiti o serie cronologica cu datele din problema si comentati tipul de indicator folosit.

2.Analizati cu cat s-a modificat C.A. atat in raport cu prima luna cat si in raport cu luna precedenta.

3.Aratati de cate ori se modifica C.A. in raport cu prima luna, cat si de la o luna la alta.

4.Aratati cu cat la suta s-a modificat

C.A. in raport cu prima luna, cat si de la o luna la alta.

5.Graficul seriei.(cronograma).