PARAMETRII REPARTITIILOR EMPIRICE UNIDIMENSIONALE

Organizarea datelor rezultate din observarea statistica sub forma de serie de frecvente, constituie o prima etapa a prelucrarii acestora. O serie statistica reda sub forma rezumativa (sintetica) o prima imagine asupra populatiei de studiat in raport cu variabila de la baza seriei.

Pornind de la repartitia statistica, ca forma sintetica de prezentare a rezultatelor observarii, se pot deduce o serie de caracteristici specifice populatiei considerate, cum ar fi:

- nivelul mediu al variabilei;

- structura populatiei in raport cu variabila considerata;

- variatia variabilei in raport cu nivelul mediu al acesteia;

- forma dupa care se dispun unitatile populatiei in jurul valorii medii. Caracterizarea numerica a acestor aspecte poate fi realizata prin urmatorii parametri (caracteristici):

- parametrii tendintei centrale;

- parametrii de structura;

- parametrii variatiei;

- parametrii concentrarii;

- parametrii formei.

Se prezinta, in cele ce urmeaza, aspecte legate de definirea, semnificatia si modalitati de calcul pentru fiecare parametru.

1. Parametrii tendintei centrale

Parametrii din aceasta grupa au menirea de a evidentia pozitia in jurul careia se grupeaza ansamblul valorilor unei variabile de la baza unei serii. Aceasta pozitie exprimata printr-un numar se numeste pozitie centrala. Ea poate fi evidentiata prin:

__

- valoarea medie (X);

valoarea mediana (M_e(x));

valoarea modaia (M₀(x).

1. Valoarea medie

Valoarea medie reprezinta principalul parametru care caracterizeaza tendinta centrala a unei repartitii statistice.

In vederea definirii parametrului valoarea medie se considera o populatie statistica studiata in raport cu variabila cantitativa X si o functie G(x₁,x₂,,x_R) unde x_i,

i = reprezinta starile variabilei X. Functia G exprima o anumita insusire esentiala, un atribut al populatiei in raport cu variabila X. Aceasta functie se numeste functie determinanta.,

Prin definitie, valoarea medie a variabilei X este parametrul care lasa invarianta functia determinanta, adica:

G(x₁,x₂,,x_R) = G ( ) (0)

Aceasta egalitate se intalneste sub denumirea de relatia lui BOIARSKI-KISINI. In functie de forma analitica a functiei G, din relatia (0) se deduce expresia analitica (indicatorul) de calcul a valorii medii

Determinarea, pe aceasta cale, a valorii medii este destul de anevoioasa. Utilizarea acesteia presupune stabilirea continutului (semnificatiei) si a formei analitice a functiei determinante G, pentru fiecare caz in parte. Dar, valoarea medie poate fi definita ca un raport a doua marimi din care se deduce aceeasi expresie pentru ca si din (0).

Exista, asadar, doua modalitati echivalente de definire a valorii medii, criteriul relatiei determinante a lui Boiarski-Kisini si criteriul raportului, ultima fiind mai accesibila. Criteriul raportului presupune raportarea volumului fenomenului cercetat la volumul populatiei. Acesta presupune cuantificarea volumului fenomenului in functie de natura lui.

Pentru a exemplifica cele prezentate mai sus, se considers populatia familiilor dintr-o localitate, cercetata in raport cu numarul de copii. Datele rezultate din observare se prezinta ca o serie de repartitie de forma:

X: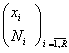

In acest caz, functia determinanta are urmatoarea forma:

G(x₁,x₂,,x_R) =

semnificand numarul total de copii din localitatea respectiva. Pentru a gasi numarul mediu de copii pe familie se particularizeaza relatia (0) dupa cum urmeaza:

=

De unde rezulta

La acelasi rezultat se putea ajunge pornind de la faptul ca numarul mediu de copii pe familie se poate exprima ca un raport intre numarul total de copii si numarul de familii din localitatea respectiva, adica:

In acest exemplu, fenomenul fiind de natura demografica, volumul acestuia se cuantifica prin numarul total de copii la nivelul populatiei statistice considerate. Aceasta este in directa concordanta cu natura si senmificatia variabileiifn raport cu care se face cercetarea statistica.

Cunoasterea 'naturii' parametrului valoare medie, conduce la o definite mai completa si plina de semnificatie. _

Pentru a intelege semnificafia valorii medii trebuie subliniat faptul ca, in general, variatia unui fenomen, de orice natura, si in particular variatia unei variabile X in raport cu care este cercetata o populate, este determinata de actiunea simultana a doua categorii de factori: factori esentiali si factori neesentiali.

In categoria factorilor esentiali intri acei factori care actioneaza asupra tuturor unitatilor populatiei in mod continuu si in acelasi sens, determinand, in principal, nivelul de dezvoltare a variabilei pentru fiecare unitate componenta din populatie.

Factorii esentiaii se conjuga in actiunea lor cu factorii neesentiali, care, in general, au un caracter aleator, sunt numerosi si neuniform raspanditi printre unitatile populatiei.

Fiecare din factorii considerati neesentiali acjioneaza numai asupra unui anumit numar de unitati din populatie. Ca urmare, acestia pot contribui fie la cresterea nivelului variabilei (pentru unele unitati din populatie), fie la scaderea nivelului variabilei (pentru alte unitati din populatie).

La randul lor factorii esentiali nu actioneaza cu aceeasi intensitate asupra tuturor unitatilor din cadml populatiei considerate, determinand, in acest fel, variatia neuniforma a variabilei respective in cadrul populatiei.

In consens cu cele sublimate mai sus, se poate afirma ca parametrul valoarea medie a unei serii statistice care are la baza variabila X, constituie acel nivel pe care 1-ar putea inregistra variabila tn cadrul populatiei cercetate in conditiile in care factorii neesentiali nu s-ar fi manifestat, iar factorii esentiali ar fi actionat asupra unitatilor din populatie cu aceeasi intensitate.

Parametrul valoarea medie, calculat pentru o serie statistica, pune in evidenta ceea ce este comun, general si esential sub aspectu! nivelului de dezvoltare al variabilei, in raport cu care este studiata o populatie.

In raport cu natura variabilei ce sta la baza seriei, cat si a formei de prczentare a indicatorilor cu care aceasta este construita, exista mai multe posibilitati de calcul a valorii medii.

Pornind de la respectare conditiei (0) se determina expresia de calcul a valorii medii.

Pentru diverse valori ale lui k, in stricta concordanta cu continutul si semnificatia functiei G, se intalnesc mai multe tipuri de medii:

media armonica (k = -1);

media aritmetica (k = 1);

media patratica (k = 2);

media cubica (k = 3);

media de ordinul k in general.

In caz concret, valoarea medie reala este aceea care se obtine prin indicatorul (mediu) rezultat fie prin aplicarea criteriului relatiei determinante, fie criteriului raportului.

Modalitati de calcul a valorii medii

Media aritmetica

Acesta este indicatorul eel mai utilizat in calculul parametrului valoarea medie a unei serii statistice, asa cum rezulta din practica statistica.

Se considera acum doua serii statistice de repartitie, una formata din frecvente absolute, iar cealalta din frecvente relative:

X: 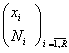(4.)

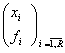X: (5.)

Avand in vedere respectarea relatiei (0) se gasesc urmatoarele expresii de calcul pentru media aritmetica:

in cazul seriilor de forma (4) se obtine:

=

De unde rezulta

In cazul seriilor de forma (5) se obtine:

=

De unde rezulta prin definitie, media aritmetica ponderata, exprimata cu ajutorul frecventelor relative, respectiv :

= (7.)

Expresia (6) reprezinta, prin definitie, expresia de calcul a mediei aritmetice ponderate pentru o serie discreta, unde ponderile sunt insasi frecventele absolute N₁,N₂,N_R.

Pentru cazul particular in care frecventele absolute sunt egale intre ele, adica:

N₁ = N2 = .= Nr = C

Relatia de calcul (6) devine:

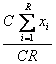= = (8.)

reprezentand media aritmetica simpla a unei repartitii discrete.

Fie o serie de repartitie, care are la baza o variabila continua X, respectiv,

X: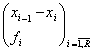

Daca s-ar cunoaste densitatea f(x) a variabilei X, atunci, prin definite, media aritmetica teoretica (speranta matematica) a acesteia, notata cu E(X), ar fi:

E(X) = (9)

Cum densitatea sa de probabilitate f(x) nu se cunoaste, aceasta se aproximeaza in fiecare interval de variable (clasa), prin raportul dintre frecventa intervalului si lungimea sa, respectiv prin:

Aplicand relapa de calcul (9') se deduce expresia de calcul a mediei aritmetice, dupa cum urmeaza:

E(X) = M(X) =

Folosind notatiile:

= M(X)=E(X) unde x_i^', reprezinta mijlocul intervalului 'i', obtinem relatia:

= (10)

Relatia(10)ne arata ca media aritmetica a unei serii de intervale se reduce la media aritmetica a unei serii discrete in care clasele sunt reprezentate prin mijloacele intervalelor de variatie.

Pentru cazul particular de serie care are la baza o variabila alternativa de forma:

X:

calculand media aritmetica, obtinem:

(11.)

Ca urmare, media aritmetica a unei serii care are la baza o variabila alternativa coincide cu frecventa relativa a starii notata cu 1.

In vederea intelegerii mai profunde a celor prezentate mai sus, se considera, in cele ce urmeaza, doua exemple concludente in acest sens.

Exemplu

Angajatii unei societati comerciale se distribuie dupa salariul lunar cuvenit conform urmatoarei serii de repartitie continua:

X :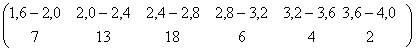

unde variabila X este exprimata in milioane lei.

In vederea determinarii salariului mediu pe angajat, se recurge la transformarea seriei de intervale intr-o serie discreta, dupa cum urmeaza:

X :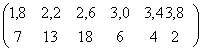

Salariul mediu se determine astfel:

= =

Presupunem ca este necesara determinarea ponderii agentilor economici, dintr-un anumit judet, care au inregistrat pierderi in anal calendaristic incheiat. Datele inregistrate de la institutiile competente se aranjeaza intr-o serie alternativa de forma:

X :

Unde starea 1 pentru variabila X corespunde acelor agenti care au inregistrat pierderi in anul considerat. Media (ponderea) agentilor cu capital de stat care au inregistrat pierderi se determina astfel:

=(15%)

In judetul considerat, 15% din agentii economici cu capital de stat au inregistrat pierderi in anul calendaristic considerat.

Proprietati ale mediei aritmetice

Prezentarea celor mai reprezentative proprietati ale mediei aritmetice prezinta importanta din punct de vedere al aplicatiilor practice, ilustrand, in acest fel si posibilitatile de calcul simplificat al acestui indicator. In acest sens prezentam urmatoarele proprietati:

I 1.Media aritmetica a unei constante este egala cu constanta respectiva, daca la baza unei serii se afla o variabila-care a inregistrat o singura stare X = C, atunci aplicand relatia de calcul a valorii medii se obtine:

M(X) = M(C ) = C

2. Media produsului dintre o variabila X si o constanta k este egala cu produsul dintre media variabilei X si constanta respectiva:

M(k*X) =

unde am considerat o serie discreta forrmata cu frecvente in acelasi mod se procedeaza pentru o serie cu frecvente absolute.

Media aritmetica a sumei a doua sau mai multe variabile este egala cu suma mediilor acestora:

M(X₁+X₂++X_R) = M(X₁)+ M(X₂) ++M(X_R)

Pentru a nu ingreuna scrierea si pentru a intelege mai bine, se demonstreaza aceasta proprietate pentru cazul a doua variabite X, Y. Se considera o populatie cercetata in raport cu cele doua variabile X si Y pentru care se cunoaste si se intentioneaza calcularea mediei M(X + Y).

4 Media produsului a r variabile doua cate doua independente este egala cu produsul mediilor acestora:

M(X₁*X₂**X_R) = M(X₁)* M(X₂) **M(X_R) (16)

Pornind de la cele patru proprietati ale mediei aritmetice se pot deduce o serie de consecinte ale acestora, frecvent intalnite in calcule statistice privind media. Prezentam in acest sens urmatoarele consecinte:

a) Facand media sumei dintre o variabila X si o constanta C se obtine suma dintre media variabilei si constanta respectiva :

M(X + C) = M(X) + C (19)

Aceasta proprietate se obtine ca o particularizare a proprietatii 3, pentru r = 2 siX₂ = C.

Daca constanta C are semnul negativ, atunci relatia (19) devine:

M(X-C) = M(X)-C

De unde rezulta:

M(X) = M(X - C) + C (20)

Aceasta ultima relatie, 20, conduce la concluzia conform careia, daca starile unei variabile cantitative cresc sau descresc cu o constanta C, atunci si media noii variabile obtinute creste sau descreste cu acea constanta.

b Daca valorile unei variabile X sunt simplificate cu o constanta, atunci media variabilei X descreste de acel numar de ori.

Daca in proprietatea 2, constanta este de forma 1/k, atunci, relatia (13)devine:   

M(X/k ) = 1/k * M(X)    (21)

De unde rezulta

M(X) = k*M(X/k)

c) Primele doua consecinte conduc la relatia de calcul simplificata a indicatorului media aritmetica. In acest sens, se face urmatoarea transformare asupra variabilei X:

Z =

unde C si k sunt doua constante, iar Z numele variabilei rezultate.

Aplicand operatorul medie asupra relatiei (22) se obtine:

M(k* Z) = M(X)-C

M(X) = M(Z)*k + C

M(X) = M (X - C/ k)    + C

Aceasta ultima relatie (23), constituie formula de calcul simplificat a mediei aritmetice. Avantajul maxim privind aplicarea acestei relatii se obtine alegand pentru constanta C starea de mijloc a seriei care are la baza variabila X, iar pentru k valoarea care reprezinta cel mai mare divizor comun al tuturor diferentelor X-C.

Formula (23) se particularizeaza dupa cum seria, care are la baza variabila X, este o serie construila cu frecvente absolute sau cu frecvente relative:

- in cazul unei serii construita cu frecvenfe absolute, de forma:

X: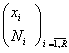

Se obtine:   

*k +C (24)

in cazul unei serii construite cu frecvente relative, de forma:

X: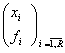

Se obtine:

*k +C (25)

Formulele (24) si (25) se aplica in mod frecvent, sub denumirea de formula de calcul simplificat, pentru determinarea mediei aritmetice, in cazul seriilor consruite cu indicatorii frecventa absolute si relativa.

d) Proprietatea de aditiune a mediei aritmetice.

Se presupune o populatie care este structurata in raport cu un criteriu C cantitativ sau calitativ, in P clase, C₁, C₂, , C_p. Atunci media aritmetica a variabilei X, in raport cu care este studiata populatia, se poate obtine ca o medie a mediilor variabilei din cele P clase.

5.Daca frecventele absolute cu care s-a construit o serie, se simplifica cu o constanta, atunci media aritmetica a seriei respective nu se modifica.

Se considera o serie de forma:

Se noteaza cu Nį'= Nį/ d , unde d reprezinta o valoare cu care se divid toate frecventele absolute.

==

Pentru a se obtine un maxim de eficienta din punct de vedere a volumului calculelor mediei aritmetice, este nevoie ca d sa fie ales drept cel mai mare divizor comun a tuturor frecventelor absolute cu care a fost construita seria.

6 Media aritmetica a unei serii este cuprinsa intre valoarea minima si valoarea maxima pe care o inregistreza variabila X, care sta la baza seriei.

Aceasta dubla inegalitate rezulta din urmatorul sir de inegalitati:

=X_max

7 Suma abaterilor liniare ale valorilor unei variabile de la media aritmetica este nula.

M(X -

8 Proprietatea de minim a mediei aritmetice, se formuleaza astfel:

M(X - )²

unde x₀ este un numar real oarecare.

Deci, valoarea medie a unei serii calculata cu media aritmetica, in sensul metricii folosite, este cea mai apropiata de ansamblul valorilor variabilei X.

2.Media armonica

Se considera o serie de forma:

X: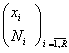

In cazul unei serii discrete de forma (27), media armonica notata cu X_-1 se defineste prin:

(28)

numita si formula mediei armonice ponderate.

Daca ponderile sunt egale intre ele, adica N₁=N₂==N_R=N*, atunci relatia(28)devine:

(29)

care reprezinta formula mediei armonice simple.

In cazul unei serii care are la baza o variabila continua X, respectiv,

X: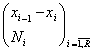

procedand ca la media aritmetica, pentru media armonica rezulta:

(30)

unde x_i reprezinta mijlocul intervalului 'i', i = l,R.

Si in acest caz, daca ponderile sunt egale, se obtine relatia de calcul a mediei armonice simple, de forma:

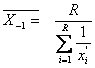(31)

Proprietati ale mediei armonice

Cateva proprietati ale acestui indicator sunt absolut necesare in vederea simplificarii volumului de calcule necesare pentru obtinerea valorii medii.

1 Media armonica este cuprinsa intre cea mai mica si cea mai mare valoare a variabilei X, inregistrata in populatia cercetata

x_min x_max

Daca valoarea medie a unei serii avand la baza variabila X, a fost calculata cu indicatorul media armonica, atunci, trebuie sa fie verificata urmatoarea relatie:

respectiv, relatia determinanta Boiarski-Kisini.

3 Media armonica a unei serii nu se modifica daca ponderile ce intervin in calculul acestui indicator se simplifica cu aceeasi constanta. Efectul maxim privind simplificarea volumului de calcule, se obtine daca se alege cel mai mare divizor comun al tuturor ponderilor, cu care urmeaza a se simplifica acestea.

4 Pentru doua serii, care au la baza aceeasi variabila X de forma:

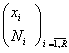X: ; X: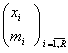

intre care exista urmatoarea relatie de legatura:

m_{i =} kx_iN_i ; i= (3,32)

media armonica apare ca oa forma transformata a mediei aritmetice.

Urmatoarele egalitati sunt relevante in acest sens:

=

Ca urmare, daca intre cele doua sisteme de ponderi m_i si N_i, exista o relatie de forma (32), media armonica este identica cu media aritmetica.

Exemplu

Se considera o intreprindere industriala formata din 5 sectii unde se cunosc productivitatile medii in fiecare sectie la nivel de muncitor cat si a realizarilor totale la nivelul fiecarei sectii. Datele din tabelul de mai jos redau acest lucru:

si sunt exprimate in mii lei.

Pornind de la acest tabel, se construieste urmatoarea serie:

X :

unde se respecta relatia m_i = x_iN_i ; Ni reprezentand numarul de muncitori din sectia i,

i = 1,5 . Ca urmare, valoarea medie a acestei serii se poate determina folosind media armonica, dupa cum urmeaza:

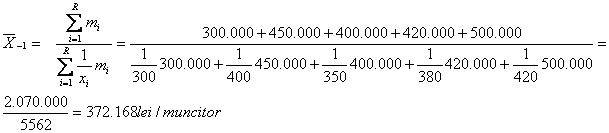
Valoarea medie, astfel obtinuta, reprezinta productivitatea medie pe muncitor la nivel de intreprindere, intr-o perioada considerata.

Media geometrica

Pentru o serie care are la baza variabila discreta X, formata cu frecvente absolute, media geometrica notata cu este definita prin expresia:

(33)

Din (33), pentru media geometrica ponderata exprimata cu frecvente relative se deduce:

(34)

Daca variabila X, de la baza seriei este de variatie continua, atunci relatiile de calcul pentru diversele variante de medie geometrica, raman variabile cu singura modificare ca valorile x_i, i = 1,R, se inlocuiesc cu mijloacele intervalelor de variatie, calculate conform formulei:

i =

Raportul intre valorile medii calculate prin indicatori diferiti

Se considera o serie care are la baza variabila X a carei valori sunt pozitive. Daca se calculeaza media acestei serii X, pe rand cu ajutorul indicatorilor: media armonica, media geometrica, media aritmetica, media patratica etc., folosind acelasi sistem de ponderi, atunci rezultatele obtinute verifica sirul de inegalitati:

, (40)

In relatia de mai sus, are loc egalitatea in cazul cand variabila X este constanta sau intre ponderi exista anumite relatii.

Deoarece nu prezinta interes studiul variabilelor care inregistreaza o singura valoare, prezinta inponanta intelegerea erorii ce poate fi comisa cand, in cazul unei serii date cu un sistem de ponderi determinat, un indicator de calcul pentru medie se substituie cu altul.

In vederea alegerii corecte a unuia dintre indicatorii de calcul a valorii medii a unei serii, trebuie folosit in functie de semnificatia variabilei, fie criteriul raportului, fie criteriul relatiei determinante.

Prin folosirea unuia duitre criterii, rezulta indicatorul care trebuie utilizat, precum si a sistemul de ponderi corespunzator in calculul valorii medii.

B. Valoarea mediana

Valoarea mediana, notata cu M_e este acea valoare a variabilei cantitative X care imparte repartitia in doua parti egale, respectiv:

F_N(M_e) = sau N(M_e) = N/2

Calculul valorii mediane se face diferentiat, dupa cum seria are la baza o variabila discreta sau continua.

Pentru o repartitie discreta, calculul medianei nu implica probleme deosebite si nici un volum mare de calcule.

Se considera o repartitie cu frecvente absolute:

X: (42)

In calculul valorii mediane a unei serii discrete, pot aparea doua situatii:

a) volumul N al populatiei este un numar impar;

b) volumul N al populatiei este un numar par.

In ambele cazuri, calculul medianei presupune, in prima faza, determinarea rangului medianei, notat cu r_M , conform urmatoarei relatii:

(40)

a) Daca volumul populatiei N este un numar impar, rangul medianei este un numar zecimal a carui parte intreaga[N/2] indica numarul de unitati din populatie pentru care variabila X a inregistrat valori mai mici ca mediana.Ca urmare M_e trebuie sa fie valoarea imediat urmatoare celei de rang [N/2], adica :

M_e = (44)

b) Daca volumul populatiei este un numar par, rangul medianei este un numar intreg si ca urmare la mijlocul seriei nu se mai afla o valoare a variabilei X cu care sa coincida mediana ci se gasesc doua valori, mediana calculandu-se in acest caz ca media aritmetica a acestora. Relatia de calcul a medianei, in acest caz, este:

M_e = 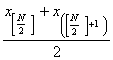(45)

Pentru o repartitie continua, calculul valorii mediane presupune

verificarea egalitatii (41) si ca urmare, trebuie cunoscuta densitatea de

repartitie f(x). Determinarea functiei implica un volum mare de calcule si

deci, din acest motiv, in activitatea practica f(x) este aproximat.

Acest lucru va conduce la o expresie aproximativa de calcul a valorii mediane, care necesita un volum redus de calcule.

Pentru acesta se considera o repartitie continua in raport cu variabila X, si anume:

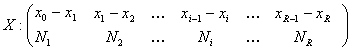(46)

unde intervalele _{Xi-1- Xi}, i = l,R pot fi de lungime egala sau neegala. Calcularea rangului medianei va permite stabilirea intervalului in care se afla valoarea mediana, interval numit si interval median. Se cumuleaza frecventele absolute din aproape in aproape pana ce este indeplinita inegalitatea:

Ultima frecventa Ni, cumulata, ne permite sa indicam intervalul median [X_i-1 - Xi).

Ca urmare, M_e , si deci se poate scrie:

M_e = (47)

unde Δx este distanta de la limita inferioara a intervalului median (X_i-1) pana la mediana. Pentru determinarea medianei mai trebuie cunoscuta aceasta distanta Δx.

Determinarea distantei Δx , de la limita inferioara a intervalului median pana la mediana se poate face in ipoteza ca in intervalul median frecventa absoluta se distribute proportional cu lungimea intervalului, de unde rezulta:

(48)

unde:

N(M_e)- reprezinta frecventa absoluta cumulata pana la mediana (rangul medianei);

N(X_i-1) - reprezinta frecventa absoluta cumulate pana la limita inferioara a intervalului median care se mai numeste si suma frecventelor intervalelor premergatoare intervalului median.

Valoarea necunoscuta Δx, rezulta din egalitatea (48):

Δx =

care intocuita in (47), permite gasirea formulei aproximative de calcul a medianei:

M_e= x_i-1+ (49)

Introducandu-se urmatoarele notatii mai sugestive:

X_i-1=X_Me- limita inferioara a intervalului median;

N_i = N_me    - frecventa absoluta a intervalului median;

x_i -x_i-1 =1_Me - lungimea intervalului median.

Aceeasi expresie de calcul a medianei este folosita si in cazul in care seria continua este formata din frecventele relative, cu urmatoarele precizari:

F_N(M_e) - reprezinta suma frecventelor relative ale intervalelor

premergatoare intervaluiui median;

f_Me ~ notatie sinonima pentru N_M reprezentand frecventa relativa a

intervalului median.

Cu aceste notatii relatia (50) devine:

Pe langa procedeul expus anterior, mai exista si un procedeu grafic de calcul a valorii medianei. Acest procedeu poate conduce la rezultate cel putin la fel de bune, mai ales in cazul seriilor care au la baza o variabila continua, deoarece, nu mai este necesara persupunerea repartizarii proportionale a frecventei in intervalul median, cu conditia ca reprezentarea grafica a seriei sa se faca cat mai exact posibil. In acest sens, se construieste poligonul cumulativ crescator al seriei si se duce o paralela la axa Ox prin punctul de ordonata *N. Abscisa punctului de intersectie a acestei paralele cu poligonul cumulativ crescator va fi valoarea mediana a seriei respective.

Proprietati ale valorii mediane

In cele ce urmeaza se vor prezenta cateva din cele mai reprezentative proprietati ale valorii mediane, care sa permita o caracterizare cat mai completa a acestui parametru sub aspectut aplicabilitatii practice.

1. Valoarea mediana a unei serii este cuprinsa intre cea mai mica si cea mai mare valoarea a variabilei care sta la baza ei:

Aceasta proprietate este evidenta insasi din definitia data parametrului, dar ea poate rezulta aplicand o serie de majorari si minorari in relatia de calcul (50).

2 Valoarea mediana a unei serii nu se modifica daca frecventele absolute se simplifica cu aceeasi valoare (de obicei, cel mai mare divizor comun).

Demonstratia acestei proprietati rezulta din formula de calcul a valorii mediane (50). Urmatorul raport:

care apare in expresia de calcul a medianei ramane invariant la simplificarea frecventelor absolute cu aceeasi valoare si ca urmare nu afecteaza marimea medianei.

Proprietatea de minim. Pentru o repartitie a carei mediana este Me , se poate arata ca dintre toti parametrii care intervin in caracterizarea seriei respective, mediana este aceea fata de care valorile individuale ale variabilei X de la baza seriei se abat cel mai putin, daca aceste abateri se iau in valoare absoluta.

Aceasta proprietate este cunoscuta si sub numele de proprietatea de minim sau de reprezentativitate a medianei.

In vederea demonstrarii acestei proprietati se considera o valoare reala x₀ oarecare si urmatoarea functie:

φ(x_o) = MX-x₀

Demonstrarea proprietatii enuntate este echivalenta cu a arata ca valoarea minima a acestei functii se atinge pentru x_o = M_e . Fara a particulariza demonstratia, se poate presupune ca x₀ se afla intre doua valori consecutive x_r si x_r+1 ale variabiiei X.

Aceasta proprietate, confera valorii mediane calitatea de a juca rolul de valoare medie. Valoarea mediana poate substitui valoarea medie in conditiile in care aceasta din urma nu poate fi calculata. De obicei, pentru serii care au la baza o variabila X continua, iar intervalele de variatie marginale sunt deschise si nu dispunem de informatii pentru a putea fi inchise, calculul valorii medii nu este posibil, caz in care mediana ii va lua locul.

Valoarea mediana prezinta unele avantaje in comparatie cu valoarea medie.

In acest sens, se amintesc cateva dintre acestea:

volumul de calcule este mai redus, deoarece, in calculul acesteia nu

intervin toate valorile variabilei;

mediana este mai putin afectata de valorile extreme ale variabilei, care uneori, pot fi anormal de mari sau de mici, situatie in care mediana este mat reprezentativa.

Cu toate aceste avantaje, totusi mediana nu poate compensa avantajele valorii medii. Mediana nu se bucura de anumite proprietati ale valorii medii, cum ar fi: media unei sume de variabile, proprietatea de aditiune.

Valoarea medie continua sa ramana parametrul care scoate in evidenta esentialul despre o populate statistica studiata in raport cu o variabila X, a carei medie se calculeaza.

C. Valoarea modala

Valoarea modala M₀(X) a unei repartitii reprezinta aceea valoare a variabilei X careia in corespunde frecventa cea mai mare.

Acest parametru se mai numeste modul, valoare dominanta, sou modala se noteaza cu M₀.

Mod de calcul:

a)      Pentru o serie de repartitie discreta, data sub forma:

X: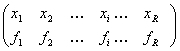(51)

valoarea modala se citeste direct din serie, nefiind nevoie de nici o tehnica sau formula de calcul. In cazul acestui tip de serie, valoarea modala va fi acea valoare a variabilei X pentru care frecventa este cea mai mare.

b) Pentru serii de repartitie continue, respectiv:

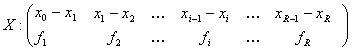(52)

modala nu poate fi determinate direct.

Intervalul caruia ii corespunde frecventa cea mai mare, se numeste intervalul modal si va contine modala. Sa presupunem ca intervalul modal este X_i-1 -X_i .

Se vor prezenta doua modalitati de calcul a modalei, una care se bazeaza pe aproximarea densitatii de probabilitate f(x) de-a lungul a trei intervale de variatie (intervalul modal si cele doua intervale cu care se invecineaza), iar cealalta metoda permite gasirea unei formule de calcul aproximativ, a carei deductie se bazeaza pe principiul repartizarii uniforme a frecventei de-a lungul intervalului modal.

Prima metoda de calcul a modalei presupune estimata densitatea de probabilitate f(x). Odata gasita f(x), valoarea modala va fi acea valoare a lui x pentru care f(x) inregistreaza valoarea maxima.

Aceasta metoda se bazeaza pe posibilitatea aproximarii densitatii f(x) de-a lungul celor 3 intervale precizate cu un arc de parabola de forma:

f(x) =ax² + bx + c

unde, a, b, c sunt trei parametri ce trebuie determinati.

Estimarea celor trei parametrii a,b si c se face utilizand metoda ariilor, conform careia suprafafa marginila de arcul de parabola, axa Ox si cele doua perpendiculare ridicate in punctele de abscisa x_i-2 si x_i+1 si suprafata celor trei dreptunghiuri care formeaza histograma seriei de-a lungul celor trei intervale, sa fie egale. Respectarea acestei conditii conduce la urmatorul sistem de ecuatii:

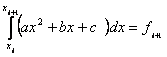
daca seria este de intervale egale.

Un calcul elementar de integrate definite printr-o functie polinomiala, transforma egalitatile (53) intr-un sistem liniar de ecuatii in necunoscutele a, b, c. Rezolvand acest sistem, se afla estimatiile pentru cei trei parametrii [5].

Determinarea modalei implica gasirea punctului pentru care f(x) isi atinge maximul. Acest punct va fi chiar modala si se calculeaza din conditia:

f^'(x)=0 (54)

Rezolvand ecuatia (54), solutia acesteia x = M₀ reprezinta valoarea modala daca mai are loc si urmatoarea conditie:

f'(M_o)<0

A doua metoda de calcul a modalei se bazeaza pe repartizarea uniforma a frecventei de-a lungul intervalului modal.

M₀=x_i-1+ x ,

unde s-a notat cu x, distanta necunoscuta de la limita inferioara a intervalului modal pana la modala. Gasirea necunoscutei x, se face din urmatoarea egalitate de rapoarte:

(57)

care semnifica repartizarea uniforma a frecventelor de-a lungul intervalului modal.

Avem urmatoarea expresie de calcul pentru x:

Atunci, formula de calcul aproximativa a modalei va fi :

unde :

M₀ -reprezinta valoarea modala;

X_Mo-reprezinta limita inferioara a intervalului modal

-reprezinta diferenta dintre frecventa intervalului modal si frecventa intervalului precedent;

- reprezinta diferenta dintre frecventa intervalului modal si frecventa intervalului urmator;

l_Mo-reprezinta lungimea intervalului modal.

2.Parametrii de structura

Frecvente sunt cazurile cand este necesara studierea structurii populatiei in raport cu o variabila sau alta.Parametrii statistici, in forma cea mai generala, folositi in caracterizarea structurii unei populatii, poarta denumirea de valori quantile.

Valorile quantile ale unei serii de repartitie unidimensionale sunt acele marimi inregistrate de variabila X, care impart seria in n parti egale ( mai precis imparte populatia in n parti egale).In acest caz se vor calcula p quantile; p=n-1.

Pentru o serie continua a carei densitate de probabilitate f(x) este cunoscuta, urmatoarea egalitate este satisfacuta de cele p quantile :

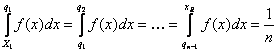(2.1.)

unde cele n-1 quantile s-au notat cu q₁, q₂,, q_n-1

Pentru o serie oarecare quantila de ordinul p, este definita astfel :

F_N(q_p)= p sau N(q_p)=

Dupa cum seria este cu frecvente relative sau absolute.

Fie o serie de repartitie care are la baza o variabila X discreta, de forma urmatoare :

X:

Pentru calculul valorii quantile de ordinul p ( p=), in prima etapa trebuie determinat rangul acesteia :

Se disting doua cazuri :

a)      Daca pn se divide cu n atunci quantila de ordin p se calculeaza ca o medie aritmetica simpla a valorilor variabilei X, de ordinul rangului si al rangului majorat cu o unitate, dupa cum urmeaza :

b)      Daca pN nu se divide cu n atunci quantila de ordin p este egala cu acea valoare a variabilei X corespunzatoare partii intregi a rangului majorat cu 1 :

In cazul seriilor care au la baza o variabila continua , cf. definitiei, cele n-1 quantile trebuie sa satisfaca relatia 2.1.

Fie o serie de variatie continua, ale carei intervale de variatie nu trebuie sa fie neaparat de lungime egala, cum ar fi :

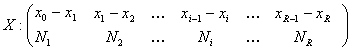
In prima etapa se determina rangul quantilei de ordinul p, conform urmatoarei relatii :

Quantila de ordinul p, se calculeaza conform relatiei :

,

unde am presupus intervalul X_i-1 -X_i ca intervalul quantilei de ordinul p, iar , reprezinta distanta necunoscuta inca, intre limita inferioara a intervalului quantilei de ordinul p si valoarea din acest interval cu care coincide quantila de ordin p.

Distanta necunoscuta se deduce astfel :

Introducem urmatoarele notatii :

,reprezinta limita inferioara a intervalului quantilei de ordinul p.

, reprezinta lungimea intervalului quantilei de ordinul p.

, reprezinta frecventa absoluta a intervalului quantilei q_p,

care conduc la formula de calcul ;

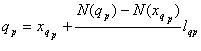(2.2.)

Valoarea mediana M_e este si un parametru de structura, obtinindu-se ca un caz particular de quantila , cand n=2.Daca pentru o serie se cunoaste quantila de ordinul 2, atunci structura populatiei poate fi redata astfel :

X :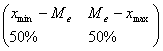

Semnificand faptul ca jumatate din populatia supusa studiului a inregistrat pentru variabila X valori cuprinse intre valoarea minima a lui X si mediana, iar cealalta jumatate din populatie a inregistrat pentru variabila X valori cuprinse intre mediana si valoarea maxima a lui X.

Formula de calcul a medianei se poate gasi ca un caz particular a relatiei 2.2.

Valorile quartile reprezinta acel caz particular al valorilor quantile pentru care n=4.Cele 3 quartile care se obtin, notate cu Q₁, Q₂, Q₃ sunt acei parametri de structura care impart populatia in 4 parti egale.

In raport cu mediana quartila intai Q₁ se numeste quantila mica (inferioara), quartila a doua Q₂ coincide cu mediana si se numeste quartila mijlocie , iar quartila a treia Q_3, se numeste quartila mare (superioara).

Valorile efective pentru cele 3 quartile se determina in mod diferit, dupa cum seria este discreta sau continua.

1.In cazul seriilordiscrete, rangul pentru cele 3 quartile se calculeaza conform formulelor :

Expresiile rangurilor pentru cele 3 quartile sunt diferite, dupa cum valorile rangurilor corespunzatoare lor sunt intregi sau nu.

In cazul in care rangurile sunt valori intregi, quartilele se calculeaza ca medie aritmetica simpla a valorilor lui X corespunzatoare rangului si rangului majorat cu o unitate.

Daca p, se divide cu 4, atunci relatiile pentru calculul quartilelor sunt :

iar daca p, se divide cu 4, atunci relatiile pentru calculul quartilelor sunt :

In cazul seriilor de variatie continua , etapele privind determinarea celor 3 quartile sunt aceleasi.

Mai intai se determina rangul quartilei, conform relatiilor :

Pentru prima quartila :

Primul interval care satisface inegalitatea :

reprezinta intervalul quartilei mici.

Acest interval fiind gasit, quartila mica se determina conform relatiei:

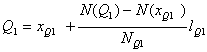
Pentru quartila mijlocie, calculele se fac ca si pentru mediana.

In cazul quartilei mari, rangul se calculeaza astfel :

Primul interval care satisface inegalitatea :

reprezinta intervalul quartilei mari.

Acest interval fiind gasit, quartila mare se determina conform relatiei:

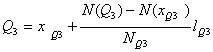
Valorile decile reprezinta acel caz particular al valorilor quantile pentru care n=10. Valorile decile reprezinta acei parametri de structura care impart populatia in 10 parti egale.

Parametrii variatiei

In functie de elementul de referinta folosit in masurarea variatiei, deosebim :

-parametrii variatiei in raport cu valoarea medie

-parametrii variatiei in raport cu valoarea mediana.

Parametrii variatiei in raport cu valoarea medie

Din aceasta grupa fac parte:

-amplitudinea sau variatia maxima

-variatia maxima si variatia minima fata de valoarea medie

-abaterea medie liniara

- abaterea medie patratica.

Amplitudinea sau variatia maxima

Acest parametru se noteaza cu W si se defineste ca fiind diferenta intre valoarea maxima si valoarea minima inregistrate de variabila.

Amplitudinea , sub forma absoluta, conform definitiei se exprima astfel:

W_x=x_max-x_min si caracterizeaza imprastierea maxima a variabilei X.

Amplitudinea , sub forma relativa, conform definitiei se exprima astfel:

sau

si masoara imprastierea intre valorile extreme ale variabilei X, in ipoteza ca valoarea medie ar fi fost 1 sau 100.

Abaterea medie liniara

Abaterea medie liniara notata cu , reprezinta media aritmetica a abaterilor variabilei X de la valoarea medie a acesteia, luate in valoare absoluta:

(1.)

Pentru o serie discreta formata cu frecvente absolute relatia 1. se particularizeaza in :

Pentru o serie discreta formata cu frecvente relative relatia 1. se particularizeaza in :

Acest parametru serveste caracterizarii sintetice a gradului de reprezentativitate a valorii medii, aratind cu cat se abate in medie orice valoare a variabilei X, de la valoarea medie, intr-un sens sau altul.

Sub forma relativa acest indicator poarta denumirea de coeficient simplu de variatie si se calculeaza conform relatiei :

Coeficientul simplu de variatie arata cu cat se abate in medie orice valoare a variabilei X de la valoarea medie echivalenta cu 1 sau 100%.

Abaterea medie patratica

Acest indicator este utilizat atat pentru caracterizarea gradului de reprezentativitate a valorii medii cat si in scopul estimarii unor parametrii necunoscuti.

Abaterea medie patratica , notata cu , se defineste ca fiind media patratica a abaterilor valorilor variabilei X, de la valoarea medie, adica:

Un calcul intermediar in aflarea acestui parametru, il constituie calcularea patratului abaterii medii patratice, care se numeste dispersie sau varianta si are urmatoarea expresie de calcul :

, aceasta fiind o alta notatie pentru varianta.

Relatia de calcul a dispersiei se particularizeaza in raport cu tipul seriei.Astfel, pentru o serie care are la baza o variabila discreta, varianta are expresia :

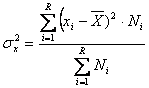pentru o serie cu frecvente absolute,

sau :

pentru o serie cu frecvente relative.

Pentru o serie data, varianta calculata nu are interpretare, dar daca se extrage radacina patrata din aceasta se obtine un numar care se exprima in aceleasi unitati de masura ca si variabila de la baza seriei. Acest numar reprezinta abaterea medie patratica, simbolizind cu cat se abate in medie in plus sau minus orice valoare x_i a variabilei X, de la valoarea medie.

Parametrul abatere medie patratica se poate exprima si sub forma relativa, caz in care se numeste coeficient de variatie a lui Pearson si se noteaza cu V_x.

Expresia de calcul este :

si reprezinta abaterea medie a oricarei valori a variabilei X de la valoarea medie, considerata egala cu 1 sau 100.

Proprietati ale variantei :

1.Varianta unei constante este egala cu 0.

V(X)=V(C)=0.

2.Varianta unei variabile X este independenta de schimbarea originii.

V(X)=V(Y)

Daca intre doua variabile Y si X exista urmatoarea relatie liniara :

Y=aX + b, atunci are loc urmatoarea egalitate :

V(Y)= a² * V(X)

4.Varianta unei variabile, fiind un moment centrat de ordinul doi, se poate exprima cu ajutorul diferentei dintre momentul de ordinul doi si patratul momentului de ordinul intai al variabilei, dupa cum urmeaza :

V(X)= M(X²)-(M(X))²

5.Varianta sumei a doua variabile X si Y este egala cu suma variantelor acestor variabile, daca cele doua variabile sunt independente.

V(X+Y)=V(X)+V(Y)

6.Varianta unei variabile X fata de o constanta x₀ este mai mare decat varianta acestei variabile fata de media sa, cu patratul diferentei dintre valoarea medie si constanta respectiva.

M(X-x₀)²=M(X

7.Varianta produsului dintre o constanta si o variabila este egala cu produsul dintre constanta la patrat si varianta :

V(a X)= a² V(X)

8.Varianta diferentei dintre doua variabile independente este egala cu suma variantelor acelor variabile.

V(X-Y)=V(X)+V(Y)

9.Varianta sumei a doua variabile dependente este egala cu suma variantelor celor doua variabile plus covarianta dintre cele doua variabile.

V(X+Y)=V(X)+V(Y)+2M((X-

10.Varianta mediei aritmetice a n variabile independente care urmeaza aceeasi lege de distributie este egala cu varianta uneia dintre variabile impartita la numarul variabilelor considerate.

11.Varianta unor variabile normate este unu, iar media este zero.

Pentru o variabila X oarecare, variabila normata atasata este :

Z=

De medie M(Z)=0.

Si varianta

12.Regula de adunare a variantelor.

Varianta in intreaga populatie, care masoara variatia totala in raport cu X, este egala cu suma a doua variante, din care una masoara variatia in cadrul grupelor, iar cealalta variatia dintre grupe.

2.Parametrii variatiei in raport cu valoarea mediana

Cand intervalele marginale ale unei serii sunt deschise, valoarea medie neputind fi calculata, valoarea mediana joaca rolul valorii medii.

In acest scop, trebuie caracterizat gradul de reprezentativitate a valorii medii, care se realizeaza cu ajutorul urmatorilor parametrii ai variatiei:

abaterea interquartila

abaterea interdecila

abaterea interquantila

Abaterea interquartila

Abaterea interquartila , prin definitie este media aritmetica simpla a segmentelor

M_e-Q₁ si Q₃-M_e, respectiv:

si arata cu cat se abat in medie in plus sau in minus, de la mediana cele 50% din valorile variabilei cuprinse intre Q₁ si Q

Forma relativa a acestui indicator , notat cu Q_r este :

se numeste coeficient de variatie interquartilic si arata cu cat se abat in medie de la mediana ( considerata egala cu 100), valorile variabilei inregistrate pentru cele 50% din unitatile populatiei cuprinse intre Q₁ si Q

Abaterea interdecila

Acest parametru ofera o imagine mult mai concludenta privind gradul de reprezentativitate.

Parametrul abaterea interdecila permite caracterizarea gradului de reprezentativitate a valorii mediane peste 80% din populatia supusa studiului si care inregistreaza valori pentru variabila, in raport cu care este studiata, cuprinse intre decila intai si decila a noua.

Abaterea interdecila se noteaza cu D si avem :

D=

Reprezentand forma absoluta a parametrului.

Raportind abaterea interdecila D la mediana si inmultind cu 100 se obtine forma relativa a acestui parametru notata cu D_r :

care se mai numeste coeficient de variatie interdecilic.Acest coeficient masoara dispersarea in medie a celor 80% din unitatile populatiei fata de valoarea medianasi serveste la compararea gradului de reprezentativitate a valorilor mediane calculate pentru diferite serii.

Gradul de reprezentativitate a medianei este cu atat mai mare cu cat abaterea interdecila este mai mica.

Abaterea interquantila caracterizeaza gradul de reprezentativitate a valorii mediene.

Pentru acest parametru sub forma absoluta, avem :

iar sub forma relativa, denumita si coeficient de variatie interquantilic este :

Cu cat abaterea interquantilica este mai mica, cu atat valoarea mediana este mai reprezentativa.

4.Parametrii concentrarii

Daca la baza unei serii se afla o variabila numerica, atunci caracterizarea sintetica a concentrarii valorilor sale in jurul valorii medii se realizeaza in principal cu ajutorul parametrilor adecvati ai variatiei.

In cazul in care seria are insa la baza o variabila nenumerica, caracterizarea sintetica a concentrarii starilor variabilei se poate realiza prin:

lungimea vectorului de structura

energia informationala

entropia informationala

Lungimea vectorului de structura

Prin definitie intr-un spatiu cu R dimensiuni , norma vectorului f , notata cu , se exprima astfel:

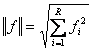
Seria prezinta o concentrare maxima daca toate unitatile populatiei sunt repartizate intr-o singura clasa a carei frecventa relativa va fi 1, iar pentru celelalte clase frecventele relative vor fi 0.

Energia informationala

Acest parametru a fost introdus de academicianul Octav Onicescu.Prin definitie :

E=, unde s-a notat cu E, energia informationala.

In cazul unei populatii caracterizate de un grad de concentrare maxim, va exista o clasa care va avea frecventa relativa egala cu 1, iar celelalte vor avea frecvente relative 0 si ca urmare E_max=1.

Daca populatia este caracterizata de o concentrare minima, atunci :E_min=1/R.

Forma relativa a acestui parametru, notata cu E_r, se deduce astfel :

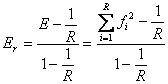, de unde .

Referitor la populatia data , studiata in raport cu o variabila X, se calculeaza E_r, iar daca :

-E_r se apropie de 1,atunci populatia respectiva este caracterizata de un inalt grad de concentrare

- E_r se apropie de 0,atunci populatia respectiva este caracterizata printr-o concentrare minima.

Entropia informationala

Pentru o serie cu frecvente relative, entropia informationala, notata cu H se defineste astfel :

H=

In cazul unei concentrari minime, entropia informationala inregistreaza o valoare maxima, deoarece :

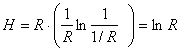
In cazul unei concentrari maxime, entropia informationala inregistreaza o valoare minima, deoarece :

H=1 ln1+ (R-1)*0*ln 1/0

Ca urmare entropia informationala verifica urmatoarea dubla inegalitate :

Formula relativa a entropiei informationale, notata cu H_r, se determina astfel :

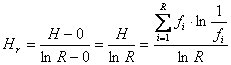
5.Parametrii formei

Parametrii formei unei serii de repartitie, dupa continut, se clasifica in doua grupe ;

-parametrii asimetriei

-parametrii boltirii

Parametrii asimetriei

Asimetria unei serii se defineste in raport cu dispunerea unitatilor intr-o parte sau alta a valorii medii.

In acest sens o serie de repartitie este simetrica in raport cu media sa daca frecventele valorilor variabilei X, egal departate de valoarea medie, sunt egale intre ele, adica :

),

oricare ar fi astfel incat sa se afle printre valorile lui X.

O serie de repartitie este asimetrica in raport cu valoarea sa medie daca exista cel putin o pereche de valori ale variabilei X, egal departate de valoarea medie, pentru care frecventele corespunzatoare sa nu fie egale intre ele, adica :

)

oricare ar fi astfel incat sa se afle printre valorile lui X.

Coeficientul de asimetrie a lui Pearson

Conform acestui parametru, o serie are o asimetrie cu atat mai pronuntata cu cat diferenta dintre valoarea medie si valoarea modala este mai mare.

Expresia de calcul pentru coeficientul de asimetrie a lui Pearson, notat cu

In raport cu valoarea obtinuta pentru , se poate aprecia gradul de asimetrie precum si sensul acesteia.

In acest sens avem :

1.daca =0, atunci , iar seria respectiva este simetrica

2.daca >0, atunci >M₀ si ca urmare, valoarea modala este situata la stinga mediei, ceea ce imprima distributiei o asimetrie pozitiva.

Coeficientul de asimetrie a lui Fisher

Acest parametru se noteaza cu ₃, iar expresia sa de calcul este :

Calculand valoarea acestui parametru, in functie de semnul ei, avem urmatoarele cazuri :

1., ceea ce inseamna ca , adica suma tuturor abaterilor cu semnul minus, este egala cu suma tuturor abaterilor cu semnul plus, ridicate la puterea a treia.In acest caz, seria este simetrica.

2. >0, ceea ce inseamna ca >0.Aceasta este echivalent cu faptul ca pe total suma abaterilor cu semnul plus de la valoarea medie este mai mare decat suma abaterilor cu semnul minus si ca urmare seria prezinta o asimetrie pozitiva.

<0, deci <0. Aceasta este echivalent cu faptul ca pe total suma abaterilor cu semnul minus de la valoarea medie este mai mare decat suma abaterilor cu semnul plus si ca urmare seria prezinta o asimetrie negativa..

Parametrii boltirii

Aprecierea boltirii unei serii este utila in caracterizarea gradului de reprezentativitate a valorii medii cat si pentru compararea reprezentativitatii a doua sau mai multe valori medii ce reprezinta serii diferite.

Parametrul da o caracterizare numerica sub forma absoluta a gradului de boltire a unei serii.

Sub forma relativa gradul de boltire a unei serii se masoara cu parametrul :

sau

unde , expresie cunoscuta sub denumirea de exces al seriei.

Urmatoarele cazuri sunt semnificative cu privire la aprecierea boltirii unei serii :

daca ( adica B₄=3) atunci seria in cauza prezinta aceeasi boltire cu a curbei normale(excesul este nul)

>0, atunci boltirea corespunzatoare curbei respective este mai inalta si mai ascutita decat curba normala

<0, atunci boltirea corespunzatoare curbei respective este mai plata ( mai joasa si mai lata) decat curba normala.

PROBLEME PROPUSE (Capitolul 3)

P1.In vederea studierii situatiei actuale pe piata actiunilor, s-a format un esantion reprezentativ de volum 40, a carui repartitie in raport cu pretul ( in mii lei) este :

X :

Se cere :

a)      pretul mediu

b)      pretul inregistrat de cele mai multe actiuni din esantion

c)      acel pret care divide esantionul in doua parti egale

d)      reprezentativitatea pretului mediu

e)      sa se calculeze cu cat se abate in medie pretul unei actiuni din esantion de la pretul mediu

f)        folosind valorile quartile sa se studieze structura actiunilor in raport cu pretul.

P2.Intr-o firma s-au realizat 40 de produse in cadrul unui trimestru.Acestea au fost propuse prelucrarii in mod secvential in doua sectii de productie.

Repartitia produselor realizate in raport cu costurile ( in mii lei) din cele doua sectii a fost :

Folosind proprietatea conform careia " media sumei a doua variabile este egala cu suma mediilor acestora", calculati costul mediu pe produs.

P.Distributia a 100 de angajati din trei ramuri de activitate diferite, in raport cu salariul primit este :

Folosind proprietatea de aditiune a mediei aritmetice sa se calculeze salariul mediu pe angajat.

P.4.Se considera o populatie statistica a agentilor ec. Studiata in raport cu volumul vinzarilor.Distributia populatiei in raport cu aceasta variabila este :

X :

Se cere :1)Sa se determine valoarea modala a seriei si interpretati rezultatul

2)Gasiti valoarea mediana si interpretati-o corespunzator.

3) Calculati abaterea medie patratica si interpretati rezultatul.

P.5. Se da urmatoarea repartitie unidimensionala avand la baza o variabila discreta, relativ la care se cere :

a) Valoarea medie si caracterizarea reprezentativitatii acesteia

b) Valoarea mediana si caracterizarea reprezentativitatii acesteia

c)Valoarea modala

d)Analiza statistica a asimetriei

e)Analiza gradului de concentrare a unitatilor

X : unde X-este numarul de copii

P.6. Se da urmatoarea repartitie statistica unidimensionala avand la baza o variabila continua, relativ la care se cere :

a) Valoarea medie si caracterizarea reprezentativitatii acesteia

b) Valoarea mediana si caracterizarea reprezentativitatii acesteia

c)Valoarea modala

d)Analiza statistica a asimetriei si a boltirii

X-reprezinta nr. de agenti economici care au inregistrat profit :

X :