INDICATORII STATISTICI

Indicatorii statistici

1. Indicatorii statistici primari si derivati

Daca se are in vedere forma de exprimare si modalitatea de obtinere atunci putem spune ca indicatorii statistici pot fi absoluti sau derivati.

Indicatorii primari se obtin in cadrul prelucrarii primare a datelor, si au un continut concret si o forma concreta de exprimare. Ei se exprima in aceeasi unitate de masura a caracteristici supuse prelucrarii statistice fapt pentru care se mai numesc si indicatori absoliti. Acesti indicatori au o mare importanta, si se regasesc pe toate structurile sistemului informational statistic si in toate fazele de agregare si dezagragare a fenomenelor.

Indicatorii primari se obtin in diverse moduri, ceea ce imprima sensuri diferite in procesul de analiza statistica. Modul de obtinere a indicatorilor absoluti se sistematizeaza astfel:

Prin insumarea directa a unitatilor componente unui fenomen complex. Numeroasele exemple de acest fel le vom intalni cand analizam sistemul de indicatori a economiei nationale. La un anumit nivel de insumare indicatorii absoluti obtinuti, pot fi considerati si indicatorii sintetici;

Prin agregarea unor valori individuale, cu acelasi continut calculat la treptele ierarhice superioare. Agregarea se deosebeste de insumarea directa prin aceea ca, nivelul fenomenului cumulat se corecteaza cu anumite elemente ce apar pe o treapta ierarhic superioara. De exemplu venitul national este un indicator sintetic absolut obtinut prin agregare, deoarece evaluarea elementelor ce-l compun se face in mod diferit in functie de treapta de agregare;

Prin obtinerea unor indicatori absoluti direct din observare, atunci cand se face un studiu monografic pentru o singura unitate statistica. De exemplu, pentru o societate comerciala cu activitate de productie indicatorii valorici ai productiei sunt in acelasi timp si indicatori absoluti inregistrati direct la nivelul unitatii.

Analiza statistica pe baza indicatorilor absoluti reprezinta un neajuns, in sensul ca nu permite o apreciere calitativa asupra fenomenului cercetat. Pentru a inlatura acest neajuns fiecare indicator absolut trebuie confruntat sau comparat cu alti indicatori sau completat cu informatii suplimentare, de natura calitativa, obtinute prin prelucrarea datelor observarii si centralizarii statistice. Cu toata aceasta limita indicatorii absoluti constituie punctul de plecare al oricarei analize statistice.

Indicatorii derivati se obtin printr-un proces de comparare, abstractizare si generalizare ce are loc in faza de prelucrare statistica a indicatorilor absoluti.

Indicatorii derivati pun in lumina aspectele cantitative ale fenomenelor si proceselor cercetate si exprima:

relatiile cantitative dintre diferitele caracteristici, dintre partile componente ale unei colectivitati sau dintre fenomenele ce se gasesc intr-un grad de interdependenta;

valorile tipice care se formeaza in mod obiectiv in cadrul aceleiasi perioade de timp sau in dinamica;

gradul si forma de variatie a caracteristicilor cercetate;

legaturile de interdependenta dintre fenomene;

tendinta obiectiva de manifestare a fenomenelor;

rolul si contributia diferitilor factori la formarea marimii unui fenomen complex, etc.

In general, indicatorii derivati se obtin prin aplicarea unui model de calcul statistic de comparare sau de estimare.

Modelul statistic de comparare se face fie pe baza de diferenta, fie pe baza de raport.

Compararea pe baza de diferenta intre doi indicatori statistici absoluti trebuie sa indeplineasca conditia de comparabilitate din punct de vedere al continutului si al formei de exprimare (unitati de masura).

Compararea pe baza de raport, are o arie mai larga de aplicare, deoarece poate fi utilizata atat pentru indicatorii care au acelasi continut, cat si pentru indicatorii care au continut diferit, dar sunt corelati. Datorita multitudinii aspectelor ce trebuie rezolvate la acest tip de comparare pe baza de raport, vom proceda la tratarea lor separat in capitolele urmatoare.

Modelul statistic de estimare se aplica pentru a estima gradul de influenta a diferitilor factori, asupra unui fenomen anlizat. Astfel, printr-o ecuatie de estimare, putem masura statistic, dependenta unei caracteristici rezultative de o serie de caracteristici factoriale sau dependenta unei caracteristici in functi de timp. Aceste aspecte vor fi tratate in temele urmatoare.

2. Marimile relative

In categoria indicatorilor derivati un loc important il detin marimile relative care se obtin pe baza raportului a doua marimi absolute si exprima printr-un singur numar proportiile indicatorului raportat fata de indicatorul baza de raportare. Sunt folosite frecvent in calculul si analiza statistica. Marimile relative se exprima in unitati sau coeficienti, procente, promile, prodecimile, procentimile etc.

Exprimarea sub forma de coeficienti ne arata cate unitati, din indicatorul absolut raportat, revin la o singura unitate a indicatorului baza de raportare. In aceasta categorie intra indicatorii de eficienta (care exprima fie raportul dintre efect si efort, fie raportul dintre efort si efect - indicatori ai consumului specific).

Exprimarea sub forma de procente, este cea mai sugestiva forma de exprimare, si ne arata cate unitati din indicatorul de raportat revin la o 100 de unitati ale indicatorului baza de raportare.

Procentele sunt analizate pentru a analiza structura unui fenomen, greutatea specifica, sau ponderea diferitelor elemente componente. De asemenea, procentele sunt utilizate si la exprimarea in dinamica unui fenomen fata de o anumita baza neschimbata sau variabila, si cand intre valorile comparate sunt diferente mici ca marime.

Exprimarea sub forma de promile, ne arata cate unitati ale indicatorului de raportat revine la 1000 de unitati ale indicatorului baza da raportare. Se folosesc atunci cand indicatorul comparat este mult prea mic fata de indicatorul baza de comparare. Acesti indicatori se folosesc in comparatiile unde coeficientii sau procentele devin nesugestive, de exemplu indicatorii miscarii naturale sau migratorii ai populatiei, eficienta fondurilor fixe, cheltuieli la o mie lei productie marfa etc.

Exprimarea sub forma de prodecimile, procentimile, etc., ne arata cate unitati lae indicatorului de raportat revine la 10.000, respectiv 100.000., etc. ale indicatorului baza de raportare. Rezultatul raportului exprimat in prodecimile, procentimile, etc., se foloseste cand comparam indicatori absoluti de valori foarte mici in comparatie cu valoarea foarte mare a indicatorului baza de raportare. De exemplu, numarul de studenti sau de medici ce revin 10.000 de locuitori, sau alte fenomene demografice (natalitatea, mortalitatea, sporul natural al populatiei etc). Oricum, in astfel de comparatii, coeficientii, procentele sau chiar promilele au valori atat de mici incat devin nesemnificative.

Calcularea marimilor relative, este precedata de o alegere atenta a bazei de comparatie si, mai ales, daca datele sunt sau nu comparabile. Forta coeficientului procentului, promilei etc., puterea mare de sintetizare si sensul economic, depinde de aceasta comparabilitate riguroasa a datelor.

Merita sa mentionam cateva aspecte care trebuie luate in considerare la asigurarea comparabilitatii datelor: unitatea in definirea notiunilor din programul observarii; modificari in modul de culegere si prelucrare a datelor statistice; folosirea unor preturi diferite la exprimarea indicatorilor valorici; surse diferite de informatii; modificari in structura organizatorica a colectivitatii inregistrate.

Marimile relative se grupeaza in urmatoarele categorii: de structura, ale planului, ale dinamicii, de coordonare si de intensitate.

Marimile relative de structura, se folosec ori de cate ori o colectivitate statistica este separata in grupe, subgrupe sau clase, dupa variatia uneia sau mai multor caracteristici de grupare sau dupa anumite criterii.

Daca notam cu "f_i" frecventele, atunci:

- suma frecventelor, (3.1)

deci:

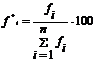(3.2)

Marimea relativa () exprima ponderea sau greutatea specifica a fiecarei frecvente in totalul acestora si este foarte des utilizata in calculul unor parametrii de distributie intr-o serie de repartitie. Suma marimilor relative de structura este intotdeauna egala cu 100. In unele situatii, marimile relative de structura se exprima si sub forma de coeficient, si atunci suma lor este egala cu unu.

Marimile relative de structura se exprima si in dinamica. Raportul dintre doua procente, exprima modificarile care au loc in structura unui fenomen, in timp, indicator deosebit de important, avand in vedere ca structura reprezinta un factor important in evolutia oricarui fenomen statistic.

Marimile relative ale planului, se folosesc ori de cate ori un fenomen se desfasoara in mod organizat, programat, planificat. Agentii economici indiferent de specificul activitatii, sunt obligati sa utilizeze acesti indicatori, fie la aprovizionare, la productie, fie la desfacerea de marfuri.

Pentru calculul marimilor relative ale planului, se introduc urmatoarele informatii privind perioadele luate in discutie:

Tabelul 3.1

In care:

y₀ = realizat in perioada de baza.

y_pl = planificat (programat) in perioada curenta.

y₁ = realizat in perioada curenta.

Pe baza celor trei elemente se calculeaza marimile relative ale sarcinii de plan si marimile relative ale realizarii planului.

- Marimile relative ale sarcinii de plan (K_pl/0), se obtin prin raportarea nivelului planificat al activitatii pentru perioada curenta sau viitoare (y_pl) si nivelul realizat in perioada de baza, premergatoare celei de plan:

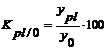(3.3)

Marimile relative ale realizarii planului (K1/pl), se obtin prin raportarea nivelului realizarilor din perioada curenta (y₁) la nivelul planificat pentru aceasta perioada (y_pl):

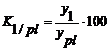(3.4)

Marimile relative ale realizarii planului, caracterizeaza gradul de realizare a sarcinilor prevazute in plan. Ele reprezinta un instrument eficace de caracterizare a activitatilor economice ale societatilor comerciale in domeniul productiei, desfacerii, productivitatii muncii, costuri, fond de salarizare, personal muncitor etc. si se interpreteaza diferit, in functie de natura fenomenului analizat.

Marimile relative ale dinamicii sunt utilizate pentru caracterizarea evolutiei fenomenelor in timp, si sunt specifice seriilor cronologice (dinamice).

Ele se calculeaza ca un raport intre nivelul fenomenului intr-o perioada si nivelul aceluiasi fenomen din perioada anterioara, considerata drept baza de comparatie si poarta numele de indicii dinamicii.

Pentru rezolvarea acestor indicatori prezentam urmatoarele informatii:

Tabelul 3.2.

Comparatia se poate face:

- fie fata de un termen reprezentativ al seriei si atunci se obtine o marime relativa de dinamica cu baza fixa:

(3.5)

de exemplu: etc.,

- fie fata de termenul precedent, si se obtine o marime relativa cu baza in lant:

(3.6)

de exemplu: etc.

Marimile relative de coordonare se prezinta ca un raport numeric intre doi indicatori absoluti de acelasi fel. Raportul acesta se face fie intre grupele aceleiasi colectivitati statistice, fie intre colectivitati statistice de acelasi fel dar situate in spatii diferite.

Marimile relative de coordonare admit propietatea de reversibilitate, si se calculeaza astfel:

(3.7)

sau:

(3.8)

in care y_A    si y_B sunt cele doua niveluri absolute comparate (fie componentele unei colectivitati, fie aceiasi colectivitate situata in spatii diferite).

(3.9)

Se exprima de regula sub forma de coeficient si au o larga aplicabilitate in comparatiile internationale dintre indicatorii sintetici ai economiei nationale.

Marimile relative de intensitate se calculeaza ca un raport intre doi indicatori absoluti, de natura diferita, dar care se afla intr-o relatie de interdependenta.

La nivelul fiecarei unitati, marimile relative de intensitate se calculeaza dupa relatia:

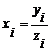(3.10)

in care:

x_i = marimea relativa de intensitate.

y_i indicatorul absolut de la numarator, care poate fi exprimat in diferite moduri, in functie de natura fenomenului analizat;

z_i indicatorul absolut de la numitor cu care este in legatura y_i.

In general exprima, cate unitati din indicatorul de la numarator revine la o unitate, la o mie, etc. din indicatorul de la numitor. La nivelul unei grupe de unitati, sau a unui ansamblu de unitati simple, marimea relativa de intensitate are continut de medie.

Din formula de mai sus se poate obtine o relatie de descompunere pe factori a indicatorului de la numarator, astfel:

(3.11)

cu semnificatia ca y_i poate fi interpretata ca o variabila rezultativa ce depinde de un factor intensiv (x_i), denumit si factor calitativ (chiar marimea relativa de intensitate) si de z_i factor extensiv, denumit si factor cantitativ, care joaca rol de pondere.

Marimile relative de intensitate, calculandu-se sub forma de rapoarte, cu baza diferite de raportare si avand continut de medie, nu se pot insuma. La nivelul ansamblului, marimea relativa se obtine nu ca o suma a marimilor relative partiale, calculate la nivelul unitatilor sau la nivelul grupelor, ci ca o medie a cestora, agregand separat numaratorul si separat numitorul, astfel:

(3.12)

In economie se calculeaza numeroase marimi relative de intensitate cum ar fi: productivitatea muncii, eficienta fondurilor fixe, inzestrarea muncii cu fonduri fixe, salariul nominal, costurile unitare, recolta la ha, venitul national pe cap de locuitor, etc. Marimile relative de intensitate se intalnesc frecvent si la calculul unor indicatori demografici, de densitate a populatiei etc.

3. Marimile medii

In categoria indicatorilor derivati, un loc important il ocupa indicatorii medii, intalniti si sub denumirea de marimi medii. Marimile medii redau ceea ce este tipic, ceea ce se manifesta ca tendinta, ca legitate in evolutia unui fenomen, din aceasta cauza ele au un grad mare de aplicabilitate in activitatea practica si in general, in cercetarile statistice.

Pentru a avea un continut cat mai real, o medie trebuie sa sintetizeze valori individuale cat mai apropiate intre ele, si sa tina seama de gradul de omogenitate al colectivitatii supuse cercetarii.

Daca totusi colectivitatea statistica este eterogena, atunci se vor calcula medii partiale, pe grupe de valori. Ele exprima raportul procentual in care se gaseste fiecare grupa sau element component, fata de totalul colectivitatii statistice.

Pentru ca marimile medii sa sintetizeze corect esentialul, este necesar sa se respecte cateva conditii:

calculul mediilor sa se bazeze pe folosirea unui numar mare de cazuri individuale diferite sub care s-a inregistrat caracteristica, a carei variatie este intamplatoare, in raport cu fenomenul in totalitatea lui;

valorile din care se va calcula media sa fie omogene;

alegerea acestei forme de medie care corespunde cel mai bine formei de variatie a caracteristicii cercetate.

Media, prin definite este expresia sintetizarii intr-o singura marime numerica a tot ceea ce este esential, tipic si obiectiv in aparitia, manifestarea si dezvoltarea unei variabile. Ea este o valoare reprezentativa pentru toate nivelurile pe care le sintetizeata, ceea ce inseamna ca media poate substitui orice nivel individual. Substituirea se poate face fie din punct de vedere cantitativ (nivelul total al caracteristicii supuse cercetarii, calculat prin totalizarea nivelurilor individuale, este identic cu acelasi total calculat cu mediile care substituie niveluirle individuale), fie din punct de vedere calitativ (semnificatia si continutul mediei depind de gradul inalt de omogenitate al unitatii statistice).

Se stie ca evolutia in timp si spatiu al unui fenomen social-economic, este influentata de intensitatea cu care actioneaza cele doua categorii de cauze: esentiale (obiective) si intamplatoare (subiective). Ori, media masoara influenta cauzelor esentiale, facand abstractie de cauze intamplatoare. Deci, media poate fi interpretata ca nivel la care ar fi ajuns caracteristica inregistrata, daca in toate cazurile, toti factorii esentiali si neesentiali, ar fi actionat constant, deci s-ar fi obtinut o valoare identica.

In sensul prezentat mai sus se poate emite ipoteza ca media este "speranta matematica", catre care tind toate valorile, variatia dintre ele nefiind altceva decat influenta factorilor aleatori. Dar, variatia este minima la fenomenele de acelasi tip calitativ si deci poate fi considerata aleatoare.

Daca fenomenele au mai multe tipuri calitative, atunci colectivitatea se imparte pe grupe omogene si atunci se opereaza cu doua tipuri de variatie: variatia din interiorul grupelor, care este influenta factorilor aleatori, si variatia dintre grupe, care este influenta unor factori esentiali care structureaza colectivitatea.

Diversitatea larga a fenomenelor social-economic, precum si complexitatea variabilitatii acestora, ne obliga sa alegem cu grija tipul de medie potrivit.

In practica statistica intalnim frecvent urmatoarele tipuri de medii: media aritmetica, media armonica, media patratica, media geometrica, media cronologica, toate acestea calculate ca medii simple sau ponderate.