Verificarea ipotezelor statistice

Verificarea ipotezelor statistice

Definitia 1. Numim ipoteza statistica o presupunere relativa la o caracteristica X a unei populatii C, fie privind legea de probabilitate a lui X, fie privind parametrii de care depinde aceasta lege de probabilitate.

Definitia 2. Metoda prin care o ipoteza statistica ce trebuie verificata se accepta sau se respinge poarta numele de test (criteriu) statistic.

Observatia Daca testul statistic se refera la parametrii de care depinde legea de probabilitate a caracteristicii X, vom spune ca avem un test parametric, iar in caz contrar avem un test neparametric. Cand testul statistic se refera la natura legii de probabilitate (normala, exponentiala, etc.) spunem ca avem un test de concordanta.

Definitia 4. Fie caracteristica X cu cu legea de probabilitate, unde este un parametru necunoscut. Ipoteza principala ce se face asupra parametrului o numim ipoteza nula si o notam . Orice alta ipoteza ce se poate face relativ la parametrul o numim ipoteza admisibila. Notam ipotezele admisibile prin , .

Observatia 5. In continuare, relativ la parametrul , vom considera numai doua ipoteze, ipoteza nula si o ipoteza admisibila , numita ipoteza alternativa.

Observatia 6. Pentru verificarea ipotezei nule cu ipoteza alternativa , folosind o probabilitate de risc , se determina un domeniu , numit regiune critica, astfel incat , unde sunt variabilele de selectie. Din felul cum construim regiunea critica U, obtinem diferite teste de verificare a ipotezei statistice . Avand datele de selectie , se poate intampla ca , caz in care ipoteza nula este respinsa, sau , caz in care ipoteza nula este admisa.

Probabilitatea de risc poarta denumirea de nivel de simnificatie al testului.

Definitia 7. Numim eroare de genul I respingerea unei ipoteze adevarate, iar probabilitatea de producere a acestei erori este

si poarta numele de riscul furnizorului.

Numim eroare de genul II admiterea unei ipoteze false, iar probabilitatea de producere a acestei erori este

si poarta numele de riscul beneficiarului.

Definitia 8. Se numeste puterea testului probabilitatea de respingere a unei ipoteze false, adica

, unde , deci .

Observatia 9. Nu exista o metoda generala de construire a regiunii critice U, care sa ne conduca la testul de verificare , dar se cunosc clase de probleme pentru care s-au construit astfel de regiuni critice si corespunzator acestora avem diferite teste de verificare de ipoteze statistice.

Vom prezenta in continuare cateva teste de verificare a unor ipoteze statistice.

1. Testul Z

Se considera caracteristica X, ce urmeaza legea normala , unde este necunoscut, iar este cunoscut.

Relativ la media teoretica facem ipoteza nula , cu alternativa .

Pentru verificarea ipotezei nule cu alternativa precizata mai inainte, consideram o selectie repetata de volum n si nivelul de semnificatie . Fie datele de selectie si corespunzator variabilele de selectie . Daca se considera statistica

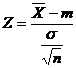, unde ,

pe baza Observatiei 1.17, avem ca statistica Z urmeaza legea normala . Prin urmare, pentru , putem determina intervalul numeric astfel incat

.

Intr-adevar, avem ca

,

asadar, se ia astfel incat .

Se defineste regiunea critica dupa cum urmeaza

,

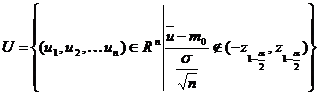unde .

In acest fel am obtinut ca

.

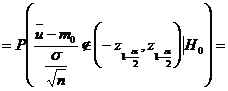
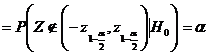Prin urmare, am determinat regiunea critica U, astfel incat sa fie satisfacuta relatia .

Folosind regiunea critica U, vom respinge ipoteza nula , daca , adica daca 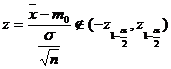si o admitem daca , adica .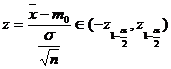

Observatia 10. Se vede ca regiunea critica U corespunde multimii complementare a intervalului numeric . Din acest motiv, in cele ce urmeaza, nu vom pune in evidenta, de fiecare data, regiunea critica U, ci numai intervalul numeric caruia ii apartine statistica utilizata pentru obtinerea acestei regiuni.

Observatia 11. Testul Z se poate folosi si pentru caracteristica X ce nu urmeaza legea normala, cand volumul n al selectiei este mare , avand in vedere ca statistica Z urmeaza aproximativ legea normala , unde si .

Observatia 12. (Etapele aplicarii testului Z).

1^o Se dau: ;

2^o Se determina astfel incat ;

3⁰ Se calculeaza 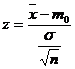, unde ;

4⁰ Concluzii: daca , ipoteza este admisa, in caz contrar ipoteza este respinsa.

Observatia 1 Deoarece ipoteza alternativa este , testul prezentat este testul Z bilateral. Daca ipoteza alternativa este , se obtine in mod analog testul Z unilateral stanga, respectiv pentru ipoteza alterantiva , se obtine testul Z unilateral dreapta.

De exemplu, pentru testul Z unilateral dreapta, intervalul numeric pentru statistica Z devine , unde este determinat astfel incat , iar regiunea critica U se modifica in mod corespunzator, adica

.

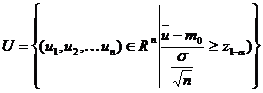2. Testul T (Student)

Se considera caracteristica X ce urmeaza legea normala cu parametrii si necunoscuti. Relativ la aceasta caracteristica se face ipoteza nula cu ipoteza alternativa .

Pentru verificarea acestei ipoteze se considera o selectie repetata de volum n, cu datele de selectie si corespunzator variabilele de selectie .

Construim statistica 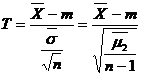, unde, dupa cum se stie , , care, conform Observatiei 1.22, urmeaza legea Student cu n-1 grade de libertate.

Prin urmare, pentru nivelul de semnificatie dat, se poate determina intervalul numeric astfel incat

.

Anume, se determina astfel ca 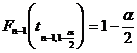, unde

,

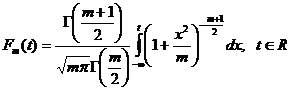este functia de repartitie pentru legea Student cu m grade de libertate (tabelata in Anexa II, pentru anumite valori).

Complementarea intervalului numeric, astfel determinat, ne defineste regiunea critica . Astfel, avem ca

,

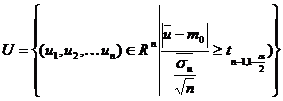unde , respectiv .

Observatia 14 (Etapele aplicarii testului T).

1^o Se dau: ;

2^o Se determina astfel incat ;

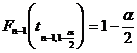3⁰ Se calculeaza 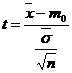, unde , ;

4⁰ Concluzii: daca , ipoteza este admisa, in caz contrar ipoteza este respinsa.

Observatia 15. Deoarece ipoteza alternativa este , testul prezentat este testul T bilateral. Daca ipoteza alternativa este , se obtine in mod analog testul T unilateral stanga, respectiv pentru ipoteza alterantiva , se obtine testul T unilateral dreapta.

Cand numarul gradelor de libertate tinde spre infinit, conform teoremei limita centrala, avem ca legea Student converge in repartitie la legea normala .

Prin urmare, daca volumul n al selectiei este mare , se poate utiliza testul Z pentru verificarea ipotezei nule , prin utilizarea statisticii T in loc de statistica Z. Toate rezultatele de la testul Z raman, asadar, adevarate in acest caz.

Teste pentru compararea a doua medii

Se considera doua populatii independente si cercetate din punct de vedere al aceleiasi caracteristici. Aceasta caracteristica este pentru si urmeaza legea normala si respectiv pentru si urmeaza legea normala .

Relativ la mediile teoretice ale celor doua caracteristici independente se face ipoteza nula cu alternativa .

Pentru aceasta se considera cate o selectie repetata de volum si respectiv din cele doua populatii. Notam datele de selectie prin si respectiv , si variabilele de selectie , respectiv

Reamintim notatiile

, ,

, ,

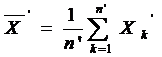pentru mediile de selectie si respectiv dispersiile de selectie.

Distingem in cele ce urmeaza trei cazuri, in functie de anumite informatii ce le cunoastem relativ la dispersiile teoretice.

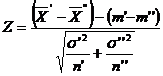a). Testul Z (daca dispersiile si sunt cunoscute). In acest caz se considera statistica , care urmeaza legea normala . Se aplica prin urmare testul Z pentru compararea celor doua medii teoretice.

Pentru nivelul de semnificatie dat se determina intervalul numeric , astfel incat . Stabilirea acestui interval se obtine din relatia , unde este functia lui Laplace si care este tabelata in Anexa I.

In acest caz, etapele aplicarii testului sunt:

1^o Se dau: ;

2^o Se determina astfel incat ;

3⁰ Se calculeaza 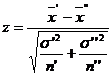, unde , si

4⁰ Concluzii: daca , ipoteza este admisa, in caz contrar ipoteza este respinsa.

b). Testul T (daca dispersiile si sunt necunoscute si 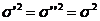). Se considera statistica

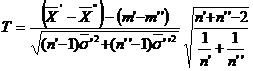, care urmeaza legea Student cu grade de libertate.

In acest caz se va aplica testul T. Pentru nivelul de semnificatie dat se poate determina intervalul numeric , astfel incat . Pentru aceasta se foloseste relatia 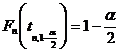, unde este functia de repartitie de la legea Student cu n grade de libertate si care este tabelata, pentru anumite argumente, in Anexa II.

Etapele aplicarii testului sunt:

1^o Se dau: ; ;

2^o Se determina astfel incat ;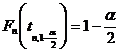

3⁰ Se calculeaza 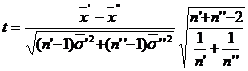, unde , , , ;

4⁰ Concluzii: daca , ipoteza este admisa, in caz contrar ipoteza este respinsa.

c) Testul T (daca dispersiile si sunt necunoscute si diferite). Se va considera statistica

,

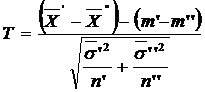care urmeaza legea Student cu n grade de libertate. Numarul n al gradelor de libertate se calculeaza cu formula , unde .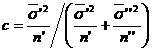

S-a ajuns la testul T, care pentru nivelul de semnificatie dat, conduce la intervalul numeric , astfel incat

.

Pentru aceasta se foloseste relatia 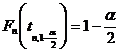, unde este functia de repartitie de la legea Student cu n grade de libertate si care este tabelata, pentru anumite argumente, in Anexa II.

Etapele aplicarii testului sunt:

1^o Se dau: ;

2^o Se calculeaza

, ,

, ,

de unde ;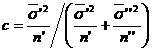

3⁰ Se determina n astfel incat ;

4^o Se determina astfel incat ;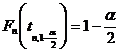

5⁰ Se calculeaza ;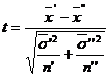

6⁰ Concluzii: daca , atunci ipoteza este admisa, in caz contrar ipoteza este respinsa.

4. Testul (hi-patrat) pentru dispersie

Fie caracteristica X ce urmeaza legea normala , unde dispersia teoretica este necunoscuta si de asemenea necunoscut.

Relativ la dispersia teoretica se face ipoteza nula cu ipoteza alternativa .

Pentru verificarea ipotezei nule cu alternativa se considera o selectie repetata de volum n, cu datele de selectie si corespunzator variabilele de selectie .

Statistic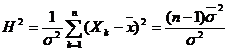a , urmeaza legea cu grade de libertate.

Pentru un nivel de semnificatie dat, se poate determina un interval numeric 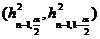astfel incat

.

Extremitatile acestui interval numeric se determina din relatiile

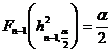si ,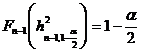

unde este functia de repartitie pentru legea cu m grade de libertate, adica 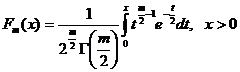, fiind tabelata pentru anumite valori in Anexa III.

Cu ajutorul intervalului numeric astfel determinat, regiunea critica va fi data de complementarea acestui interval, adica

,

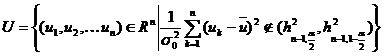unde .

Observatia 16 (Etapele aplicarii testului ).

1^o Se dau: ;

2^o Se determina intervalul 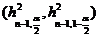astfel incat

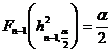si ;

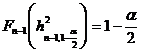3⁰ Se calculeaza , unde ;

4⁰ Concluzii: daca , ipoteza este admisa, in caz contrar este respinsa.

5. Testul F (Snedecor-Fisher)

Se considera doua populatii independente si cercetate din punct de vedere al aceleasi caracteristici. Aceasta caracteristica este pentru si urmeaza legea normala si respectiv pentru si urmeaza legea normala .

Relativ la dispersiile teoretice ale celor doua caracteristici se face ipoteza nula cu alternativa .

Pentru verificarea ipotezei nule se efectueaza cate o selectie repetata de volum respectiv si din cele doua populatii si . Notam datele de selectie prin si respectiv , si variabilele de selectie , respectiv

Cu notatiile

, ,

,

avem ca statistica , urmeaza legea Snedecor-Fisher cu si grade de libertate. Prin urmare, statistica F are functia de repartitie, pentru , data prin

.

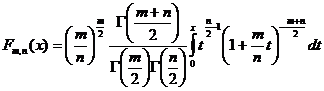Pentru un nivel de semnificatie fixat se poate determina intervalul numeric , astfel incat

.

Extremitatile acestui interval se determina din relatiile

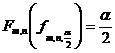si .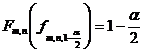

Deoarece are loc relatia , tabelele pentru functia sunt, de regula, intocmite numai pentru valori mari ale lui (0,95, 0,975, 0,99 in Anexa IV) si pentru .

Daca , intervalul numeric pentru F este dat prin

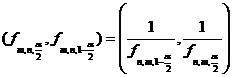
Observatia 17 (Etapele aplicarii testului F).

1^o Se dau: ;

2^o Se determina intervalul astfel incat

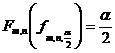si ;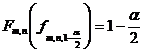

3⁰ Se calculeaza , unde

, ,

,

4⁰ Concluzii: daca, atunci ipoteza este admisa, in caz contrar este respinsa.

6. Testul de concordanta

Fie caracteristica X, care are functia de repartitie teoretica F. Ipoteza statistica nula ce o facem relativ la caracteristica X este

,

unde sunt parametri necunoscuti.

Pentru a verifica aceasta ipoteza statistica, la inceput, folosind datele de selectie , se estimeaza prin metoda verosimilitatii maxime parametrii . Fie estimatiile de verosimilitate maxima pentru acesti parametri, respectiv . Prin urmare, ipoteza nula devine .

Se efectueaza apoi gruparea datelor de selectie , conform Observatiei 1.11 si Observatiei 1.12, obtinandu-se distributia empirica de selectie 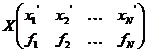. Pentru clasa , data de intervalul avem ca , , probabilitati necunoscute, deoarece functia de repartitie teoretica F este necunoscuta.

Din ipoteza nula se poate calcula probabilitatea

.

In acest fel ipoteza nula , facuta asupra functiei de repartitie, se poate rescrie in , cu ipoteza alternativa falsa.

Valoarea numerica este valoarea unei variabile aleatoare ce urmeaza legea de probabilitate cu grade de libertate.

Asadar, pentru probabilitatea de risc se considera intervalul de incredere pentru , definit prin relatia

, adica .

Aici functia este functia de repartitie pentru legea cu numarul gradelor de libertate si care este tabelata in Anexa III.

Observatia 18 (Etapele aplicarii testului ).

1^o Se considera: ;

2^o Se determina estimatiile de verosimilitate maxima ;

3⁰ Se determina distributia empirica de selectie ;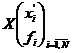

4^o Se calculeaza probabilitatile

, ;

5⁰ Se calculeaza astfel incat ;

6⁰ Se calculeaza ;

7⁰ Concluzii: daca , ipoteza statistica este admisa, in caz contrar ipoteza este respinsa.

Observatia 19. Testul de concordanta nu este aplicabil daca exista mai mici decat 5, caz in care se cere o regrupare a datelor de selectie.

7. Testul de concordanta al lui Kolmogorov

Fie caracteristica X de tip continuu, avand functia de repartitie teoretica F. Daca este functia de repartitie de selectie, conform Corolarului 1.27, avem ca

, unde , iar este functia lui Kolmogorov si este tabelata in Anexa V.

Se face ipoteza nula ca X urmeaza legea de probabilitate data de functia de repartitie . Daca ipoteza nula este adevarata, pentru probabilitatea de risc , se poate determina valoarea astfel incat .

Astfel, avem sau .

Asadar, daca valoarea calculata a lui pentru datele de selectie, satisface inegalitatea , vom admite ipoteza nula, in caz contrar o respingem.

Observatia 20 (Etapele aplicarii testului Kolmogorov).

1^o Se considera: , distributia empirica de selectie 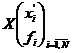, functia de repartitie , ;

2^o Se calculeaza astfel incat ;

3⁰ Se calculeaza , unde ;

4^o Concluzii: daca , ipoteza nula este admisa, in caz contrar ipoteza este respinsa.