CARACTERISTICILE GEOMECANICE ALE SARII GEME

Asa cum se prezinta in literatura de specialitate [13], [27], [30] masivul de roca sau de substanta minerala utila este un mediu greu de cunoscut, pe baza teoriilor mecanicii mediului continuu, previziunea in acest sens a comportamentului fiind aproximativa si nesigura. O asemenea afirmatie rezulta din realitatea ca masivul de roca sau substanta minerala utila este un mediu natural, discontinuu, eterogen si anizotrop. Consecintele acestor patru caracteristici fundamentale sunt multiple si pun probleme dificile industriei miniere in general, cercetatorilor si proiectantilor in principal. Pentru a defini in sensul precizat un asemenea masiv, pentru a putea calcula cu certitudine deformatiile acestuia pe baze calitative si cantitative, este necesara cunoasterea proprietatilor acestuia.

O cunoastere a caracteristicilor rocilor, respectiv substantelor minerale utile, este esentiala in orice investigatie a mecanicii rocilor, legata fie de domeniul mineritului, al constructiilor hidrotehnice, industriale, rutiere etc., fie de insasi procesele tehnologice de sapare, perforare, impuscare, taiere sau excavare.

In aceasta lucrare, fiind vorba de stabilitatea unor excavatii subterane - cunoasterea caracteristicilor geomecanice ale sarii, in principal, capata o importanta deosebita. Deoarece in numeroase lucrari de specialitate [1], [13], [27] sunt descrise in detaliu metodele de determinare a caracteristicilor geomecanice, in lucrarea de fata se vor reda sub forma tabelara numai relatiile de calcul ale acestor caracteristici cu precizarea marimilor determinate de diferite institutii in decursul timpului, astfel ca in final sa se poata desprinde anumite concluzii.

Proprietatile fizice

Studierea caracteristicilor fizice este conditionata de faptul ca parametrii de soliditate ai rocilor depind intr-o mare masura de starea fizica a lor si odata cu trecerea timpului, acesti parametri se modifica sub influenta diversilor factori. Cunoasterea starii fizice a rocilor si a influentei acesteia asupra stabilitatii masivului de roca se poate realiza numai prin studierea unor proprietati fizice, iar metodele de determinare si relatiile de calcul pentru caracteristicilor fizice sunt redate in tabel 3.1.

Tabel 3.1. Metodele de determinare si relatiile de calcul pentru caracteristicile fizice ale rocilor

Tabel 3.1. (continuare)

Proprietatile mecanice ale rocilor

Cunoasterea din punct de vedere mecanic a unui masiv de roca consta dintr-o evaluare calitativa a reactiunii acestuia in raport cu modificarile geometrice si de sarcina ce intervin in timp si realizarea de masuratori cantitative a parametrilor utilizati in calculul numeric al modului de comportare a rocilor, in cadrul diferitelor procese tehnologice de extragere, derocare si de comportare a constructiilor miniere - stabilitate.

Dintre parametrii de rezistenta ai rocilor, cei mai importanti sunt: rezistenta de rupere la compresiune monoaxiala determinata static si dinamic, rezistenta de rupere la tractiune statica si dinamica, rezistenta de rupere la incovoiere, rezistenta de rupere la forfecare, coeziunea si unghiul de frecare interioara si rezistenta de rupere la compresiune triaxiala.

Metodele de determinare si relatiile de calcul pentru caracteristicile mecanice sunt redate in tabel 3.

Tabel 3. Metode de determinare si relatiile de calcul pentru caracteristicile mecanice ale rocilor

Tabel 3. (continuare)

Caracteristicile elastice ale rocilor si substantelor minerale utile

Solicitarile unui masiv de roca, ca proces fizic izoterm, sunt legate de transformarile energetice care au loc in procesul de deformare.

Procesul fizic izoterm, un proces termodinamic, teoretic este reversibil numai atunci cand se va produce cu viteze infinit mici. Viteza cu care se produce deformarea rocilor este insa finita, ceea ce are ca rezultat disiparea unei parti din energia cumulata sub forma de caldura.

Elasticitatea rocilor poate fi pusa in evidenta prin curba caracteristica, modulul de elasticitate determinat prin solicitari statice, dinamice si coeficientul lui Poisson, determinat prin solicitari statice si dinamice.

Metodele de determinare si relatiile de calcul pentru caracteristicile elastice ale rocilor sunt redate in tabel 3.3.

Tabel 3.3. Metode de determinare si relatii de calcul pentru caracteristicile elastice ale rocilor

Tabelul 3.3. (continuare)

Caracteristici reologice

Reologia este o stiinta consacrata studierii legilor fizice de deformare a sistemelor materiale. Prin intermediul ei se studiaza influenta factorului timp in procesul de deformare si rupere. Ca urmare, reologia rocilor studiaza deformatiile acestora sub efectul tensiunilor care le sunt aplicate, tinand cont de viteza de aplicare a acestor tensiuni si, mai general, de variatia deformatiilor sau a tensiunilor functie de timp. Din punct de vedere aplicativ, incercarile reologice sunt materializate cel mai frecvent prin incercari de fluaj.

Pentru conditiile de stabilitate ale excavatiilor saline, aceste incercari de fluaj au cautat sa determine fie parametrii reologici, fie modelul matematic al acestora. In tabel 3.4 sunt prezentate relatiile de determinare ale parametrilor reologici.

Tabel 3.4.Relatiile folosite pentru determinarea parametrilor reologici ai rocilor.

Caracteristicile geomecanice ale sarii geme din Romania

In vederea dimensionarii complexului camera-pilier-planseu este necesar sa se cunoasca:

felul, marimea si repartitia starilor de tensiune in elementele de rezistenta;

caracteristicile fizice, mecanice, elasto-plastice si reologice ale sarii geme din care sunt constituite elementele de rezistenta;

felul si marimea deformatiilor pe care le sufera elementele de rezistenta sub actiunea propriei greutati si a solicitarilor exterioare.

In ceea ce priveste caracteristicile sarii geme din Romania, inca din 1935 prof. M. Stamatiu a facut o serie de determinari ale rezistentei de rupere la compresiune, tractiune, incovoiere, forfecare si trasarea curbelor caracteristice pentru sarea de la Slanic, Targu Ocna, Ocna Dej, Ocna Mures si Ocna Sugatag, rezultatele acestor incercari fiind prezentate in tabelele 3.5 - 3.8.

Tabel 3.5. Rezistentele medii de rupere la compresiune ale sarii din Romania in functie de dimensiunile epruvetelor, dupa M. Stamatiu.

Tabel 3.6.Rezistenta de rupere la tractiune a sarii geme romanesti, determinata    pe probe in forma de piscot cu S = 5 cm², dupa M. Stamatiu

Tabel 3.7.Rezistenta de rupere la incovoiere a sarii geme romanesti, determinata pe placi de

20 x 20 x 5 cm si S = 100 cm², dupa M. Stamatiu

Tabel 3.8. Rezistenta de rupere la forfecare dubla a sarii geme romanesti determinata pe prisme de 20 x 12 x 8 cm si S = 96 cm², dupa M. Stamatiu

In urma acestor incercari, prof. M. Stamatiu concluzioneaza ca rezistenta la compresiune nu este o marime constanta, aceasta depinzand atat de forma esantionului cat si de marimea acestuia.

Astfel, pentru incercarile pe cuburi, prof. M. Stamatiu, ajunge la concluzia ca rezistenta la compresiune creste odata cu cresterea dimensiunilor liniare, fig. 3.1.

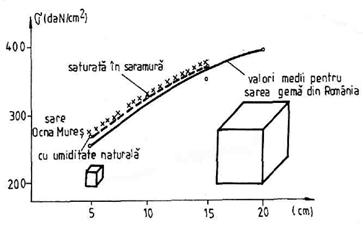
Fig.3.1. Variatia rezistentei medii de rupere la compresiune a sarii geme

din Romania in functie de dimensiunile cuburilor (dupa M. Stamatiu)

De asemenea, el a mai stabilit ca rezistenta la compresiune a epruvetelor in forma de prisme cu baza patrata scade odata cu cresterea inaltimii acestora, fig.3.

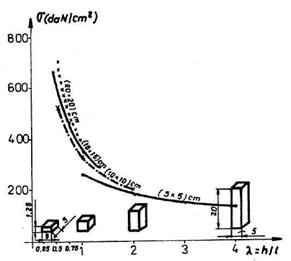
Fig.3. Variatia rezistentei de rupere la compresiune a sarii geme din Romania

- valori medii - in functie de coeficientul de sveltete (dupa M.Stamatiu)

Pe baza acestor incercari, M. Stamatiu stabileste si dependenta dintre parametrii mecanici, dependenta redata in tabel 3.9.

Tabel 3.9. Dependenta dintre caracteristicile mecanice dupa M. Stamatiu

unde:

- rezistenta de rupere la tractiune;

- rezistenta de rupere la compresiune;

- rezistenta de rupere la forfecare;

- rezistenta de rupere la incovoiere.

Incepand cu anul 1955, au fost realizate o serie de incercari geomecanice ale sarii geme in cadrul laboratoarelor de Mecanica rocilor de la Universitatea din Petrosani si, ulterior, in laboratoarele apartinand ICPMC Bucuresti si S.C. MINESA - ICPM S.A. Cluj-Napoca. Cateva din incercarile realizate in laboratorul de Mecanica rocilor de la Universitatea din Petrosani sunt prezentate in tabelele 3.10 - 3.14 si ele se refera mai ales la caracteristicile fizice si mecanice.

In ceea ce priveste caracteristicile elastice, plastice si reologice, numarul de determinari fiind relativ mare, s-au ales pentru exemplificare determinarile realizate de Universitatea din Petrosani in anul 2000 [15] prezentate in cele ce urmeaza.

Tabel 3.10.Caracteristicile fizice medii ale sarii geme din Romania determinate la Universitatea din Petrosani.

Tabel 3.11.Rezistenta de rupere la compresiune - valori medii determinate la Universitatea din Petrosani

Tabel 3.1Rezistenta de rupere la tractiune - Metoda Braziliana - valori medii determinate la Universitatea din Petrosani

Tabel 3.13.Rezistenta la forfecare dubla - valori medii determinate la Universitatea din Petrosani

Tabel    3.14.Coeziunea si unghiul de frecare interioara - valori medii determinate la

Universitatea din Petrosani

In urma incercarilor realizate cu ocazia dimensionarii planseului de sare pentru campul II de sonde Teica - Ocnele Mari, au fost intocmite tabelele 3.15 si 3.16 ca valori acceptate in anul 2000 pentru calcule de stabilitate.

Tabel 3.15. Valorile medii ale caracteristicilor fizice, mecanice, elasto-plastice si de dilatanta

ale sarii de la Ocnele Mari(Contract cu Ocnele Mari anul 2000)

Tabel 3.16. Caracteristicile si parametrii reologici ai sarii de la Ocnele Mari

(Contract cu Ocnele Mari anul 2000)

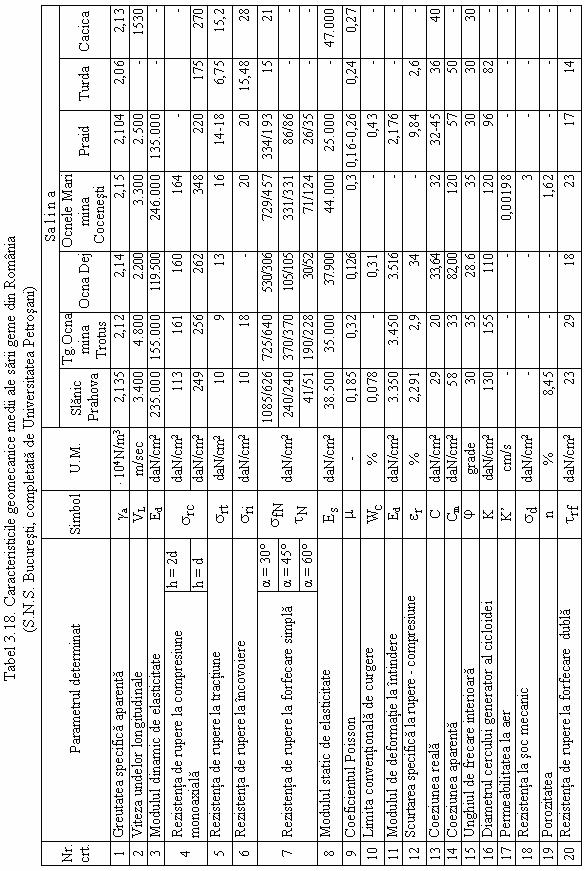
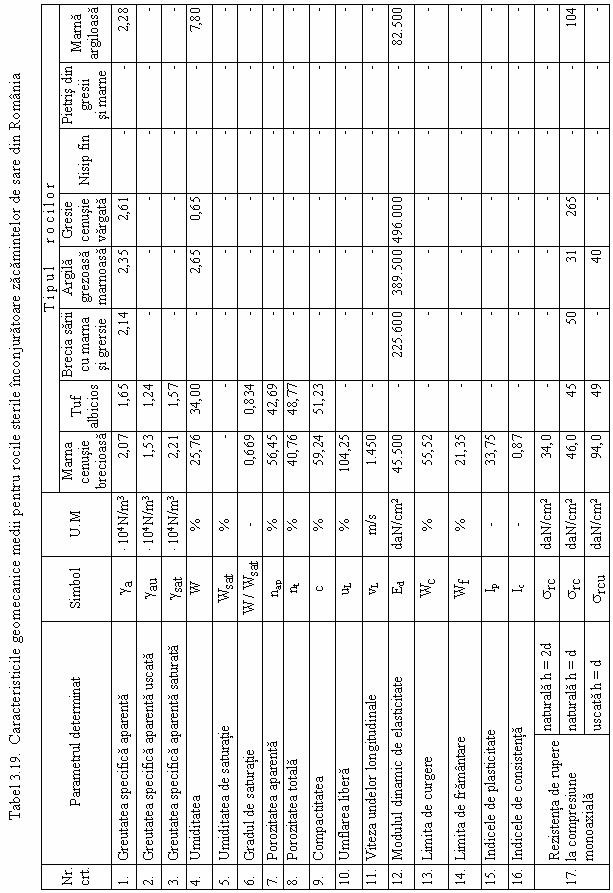
In perioada urmatoare, au mai fost realizate caracteristici geomecanice de catre I.C.P.M. Cluj Napoca, tabel 3.17. si de catre S.N.S. Bucuresti, tabelele 3.18 si 3.19.

In lucrarea de fata, noi am sintetizat toate aceste incercari si am stabilit valorile medii valabile in calculele de proiectare, tabel 3.20.

Tabel 3.17 Caracteristici geomecanice ale sarii de la Cocenesti (I.C.P.M. Cluj Napoca)

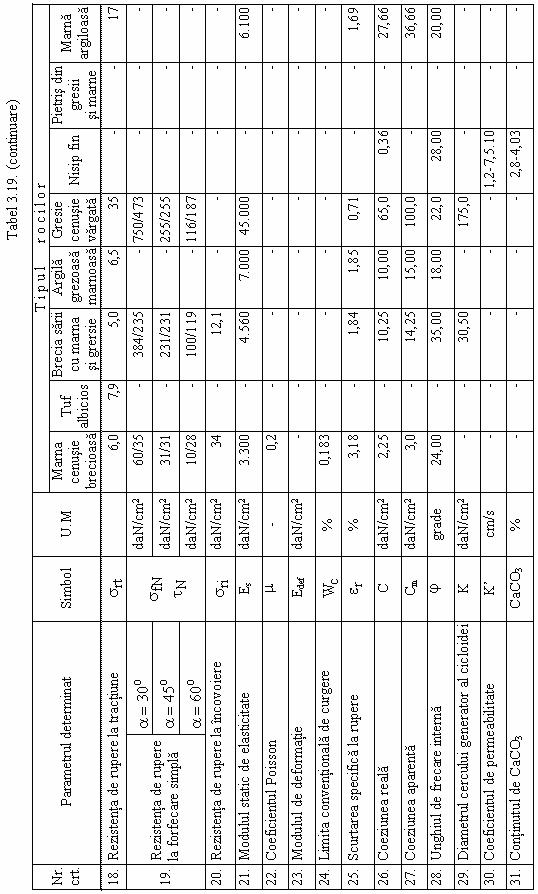
In urma numeroaselor incercari, realizate in ultimii 50 de ani, putem desprinde urmatoarele concluzii referitoare la principalele caracteristici geomecanice ale sarii de la Valcea.

Greutatea specifica aparenta variaza in limite restranse astfel incat valoarea de N/m³ poate fi acceptata fara rezerve.

Rezistenta de rupere la compresiune fiind functie de forma si marimea esantionului, variaza destul de mult, insa, daca ne referim la incercarile standardizate pe cilindrii, putem accepta valoarea de (200 - 220) daN/cm

Rezistenta la tractiune variaza de asemenea in limite largi in functie de forma esantionului - piscot, cilindru, forma neregulata - insa daca ne referim la metoda Braziliana care este standardizata, putem accepta valoarea de 10 - 14 daN/cm

Coeziunea si unghiul de frecare interioara variaza in limite largi, dupa modul de determinare - cercurile lui Mohr, forfecare, triaxial - insa valorile obtinute in aparatul triaxial si care ne dau daN/cm² si φ = 30^o par sa fie cele mai realiste pentru sarea din Romania si inclusiv pentru Cocenesti.

In ce priveste celelalte caracteristici, pentru Cocenesti - Valcea pot fi acceptate valorile din tabelele 3.20 si 3.16.

Tabel 3.20. Valorile medii ale caracteristicilor rocilor acoperitoare si ale sarii geme de la Ocnele Mari: [15]

Tabel 3.20. (continuare)