| CATEGORII DOCUMENTE |
| Comunicare | Marketing | Protectia muncii | Resurse umane |
DIMENSIONAREA TEHNICA A FUNCTIILOR
In acelasi mod in care produsele au pentru utilizator semnificatii diferite, tot la fel si functiile produsului participa la satisfacerea necesitatii in mod diferit
Principiul proportionalitatii, conform caruia intre utilitatea fiecarei functii si costul acesteia trebuie sa existe un raport constant impune cunoasterea de catre proiectantul de produs a importantei pe care utilizatorul o acorda functiilor, pentru ca la randul lui sa acorde aceeasi importanta in consumul de resurse necesare
Utilitatea (valoarea de intrebuintare) unui produs este maxima (adica atinge valoarea 1 sau 100%) atunci cand toate functiile sale sunt realizate la nivel maxim. Un astfel de produs poate fi considerat ideal sau perfect in raport cu alte variante ale aceluiasi produs, in care functiile nu sunt realizate la nivel maxim sau chiar lipsesc.
Daca se noteaza produsul perfect (ideal) cu P0, atunci utilitatea acestuia este:
![]()
Utilitatea produsului este rezultatul insumarii utilitatii functiilor sale, conform relatiei (2):
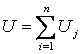
In particular, pentru produsul perfect (ideal) P0 :
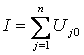
unde: Uj0 reprezinta valoarea ideala a utilitatii functiei Fj in cadrul produsului perfect
In literatura de specialitate, aceasta marime se intalneste sub denumirea de pondere sau importanta relativa a functiei si se noteaza cu qj.
Pentru o varianta oarecare a produsului, utilitatea functiei se determina cu relatia (4).
![]()
unde: uj reprezinta utilitatea intrinseca a functiei Fj , adica gradul in care varianta respectiva a functiei satisface pretentiile maxime ale utilizatorului.
In consecinta, pentru a determina utilitatea functiei sunt necesare doua actiuni distincte:
Stabilirea ponderii functiilor in utilitatea produsului ideal
Determinarea utilitatii intrinseci a fiecarei functii, adica dimensionarea tehnica a functiilor
1 Determinarea nivelurilor de importanta si a ponderilor functiilor in valoarea de intrebuintare a produsului
Din punct de vedere formal, determinarea nivelurilor de importanta a functiilor unui obiect este o operatiune relativ simpla, dar necesita cunoasterea produsului in detaliu, a conditiilor in care acesta functioneaza precum si a necesitatilor sociale pe care le satisface.
Observatii:
functie este o valoare de intrebuintare determinata de dimensiunile ei tehnice
Valorile de intrebuintare ale functiilor sunt inegale si deci fiecare functie participa in mod diferentiat la intregirea valorii de intrebuintare a obiectului (fapt ce ne indreptateste sa le ierarhizam in raport cu importanta necesitatii sociale satisfacute)
Procedee pentru determinarea importantei functiilor
a. Procedeul compararii functiilor doua cate doua
Se construieste o matrice patrata (tabelul 1) in care functiile principale si necesare se inscriu atat pe prima linie (notatie Fj ), cat si pe prima coloana (notatie Fk ).
Se compara functia Fj cu functia Fk si daca se considera ca functia Fj este mai importanta ca functia Fk (Fj >Fk), casuta kj se va completa cu cifra 1, (akj=1), iar casuta simetrica fata de diagonala principala se va completa cu cifra 0, (ajk=0).
Observatii:
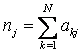

|
F1 |
F2 |
Fj |
FN |
|||
|
F1 | ||||||
|
F2 | ||||||
|
Fk |
|
akj | ||||
|
FN | ||||||
|
nj |
n1 |
n2 |
nj |
nn |
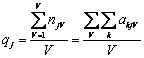
b. Procedeul ordonarii directe
Fiecarei functii i se atribuie o nota (Wj) , cuprinsa intre 1 si numarul total de functii (N), in raport cu importanta sau "valoarea" fiecareia
|
Fj |
Wj |
|
F1 |
W1 |
|
F2 |
W2 |
|
Fj |
Wj |
|
FN |
WN |
|
Total |
|
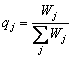 Ponderea functiei Fj in valoarea de intrebuintare a
produsului se calculeaza conform relatiei
Ponderea functiei Fj in valoarea de intrebuintare a
produsului se calculeaza conform relatiei
Unde Wj reprezinta nivelul de importanta al functiei Fj
Daca numarul persoanelor chestionate este V, atunci ponderea qj se va calcula cu relatia
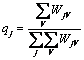
Dimensionarea tehnica a functiilor
Orice functie masurabila obiectiv are cel putin o caracteristica de calitate cu ajutorul careia se poate aprecia utilitatea ei
intre aceasta caracteristica si utilitatea functiei neexistand neaparat o relatie liniara
Daca unitatea de masura a caracteristicii de calitate se alege astfel incat utilitatea sa creasca odata cu cresterea marimii caracteristicii (numita dimensiune tehnica), atunci intre cele doua marimi exista o legatura (corelatie) de tipul celei prezentate in figura
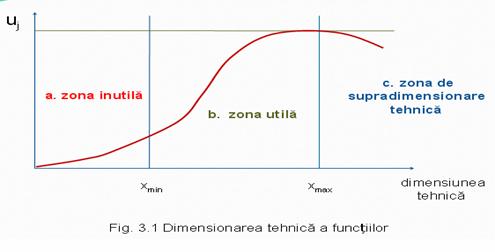
a. zona inutila - corespunde unei dimensiuni tehnice x < xmin
In aceasta zona, utilitatea functiei este atat de mica incat cumparatorul nu este satisfacut si nu va cumpara produsul
b. zona utila - corespunde unei dimensiuni tehnice xmin ≤ x ≤ xmax
c. zona de supradimensionare tehnica - corespunde unei dimensiuni tehnice x > xmax
In aceasta zona, utilitatea functiei este atat de mare incat pentru cumparator nu are semnificatie si acesta nu este dispus sa plateasca pentru achizitionarea produsului
Observatii:
E1: Este dispus un cumparator sa plateasca pentru un perete de grosime dubla fata de cea normala ?
E2: Este dispus un cumparator sa plateasca pentru o haina cu o durabilitate infinita?
E3: Este dispus un cumparator sa plateasca pentru un televizor extrem de mare?
2.1 Corelatia simpla intre utilitatea si dimensiunea tehnica a functiei
Cazul cel mai simplu si frecvent este cel al functiilor a caror utilitate poate fi apreciata prin intermediul dimensiunii unei caracteristici tehnice
Cazul prezentat in figura 1 sugereaza o corelatie neliniara, cu saturatie si intoarcere, poate fi modelat prin diverse functii (exponentiale, polinomiale, trigonometrice, transcedentale, logistice etc) care la randul lor pot fi aproximate prin segmente de dreapta
a. Corelatia de tip Cobb-Douglas
![]()
Unde x reprezinta dimensiunea tehnica
Pentru determinarea parametrilor A, a, b, se iau in considerare conditiile limita
Din conditia ca derivata de ordinul intai sa se anuleze in origine si pentru x = xmax rezulta
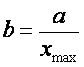
iar din conditia
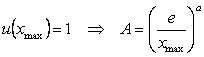
Pentru determinarea parametrului a, este necesara o a treia conditie. Daca de exemplu se doreste plasarea puncului de inflexiune la mijlocul intervalului, atunci rezulta pentru utilitate expresia din relatia
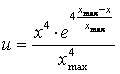
b. Corelatia de tip "dreapta prin originea axelor"
![]() Corelatia proportionala intre utilitatea
functiei si marimea caracteristicii este prezentata in
relatia
Corelatia proportionala intre utilitatea
functiei si marimea caracteristicii este prezentata in
relatia
![]()
Conditia limita permite sa se determine valoarea lui k
![]()

si anume rezultand expresia utilitatii conform relatiei
c. Corelatia liniara intre xmin si xmax
Daca pentru dimensiuni tehnice mai mici decat xmin, utilitatea functiei este aproape zero, crescand apoi liniar, atunci legea de corelatie este prezentata in relatia
![]()
![]()
Din conditia rezulta expresia utilitatii din relatia
![]()
Observatie:
Relatia de mai sus reprezinta expresia utilitatii obtinute prin interpolare liniara propuse de vonNeumann si Morgenstern
d. Corelatia logistica
O functie asemanatoare cu functia Cobb-Douglas este corelatia logistica prezentata in relatia
![]()
Conditiile limita sunt:
![]() u 1 pentru x = xmax (u = 0,99);
u 1 pentru x = xmax (u = 0,99);
u = 0,5 pentru
u 0 pentru x = 0 (u=0,01)
![]()
Rezulta:
Functia de utilitate are expresia data in relatia
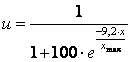
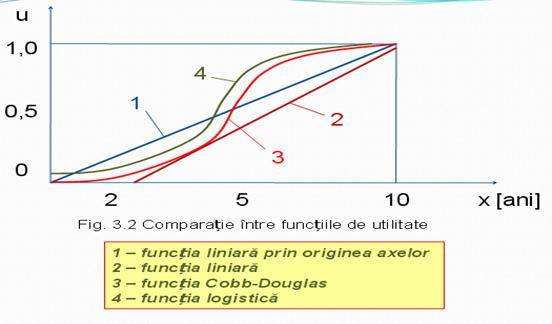
2.2 Comparatie intre functiile: "liniara prin originea axelor";"liniara"; "Cobb-Douglas" si "logistica"
Pentru a putea alege dintre una din expresiile utilitatii, este necesara o analiza comparativa a acestora
Se considera o functie generala (intalnita la aproape toate produsele) functia "este fiabil" sau functia "prezinta fiabilitate"
Se considera ca dimensiunea tehnica a functiei este "durata de viata" (in ani), cu valori cuprinse intre 2 si 10 ani
Functiile de utilitate care se compara sunt:
1 - functia liniara prin originea axelor
2 - functia liniara
3 - functia Cobb-Douglas
4 - functia logistica
In tabelul 2.3 sunt prezentate valorile comparative pentru cele 4 functii:
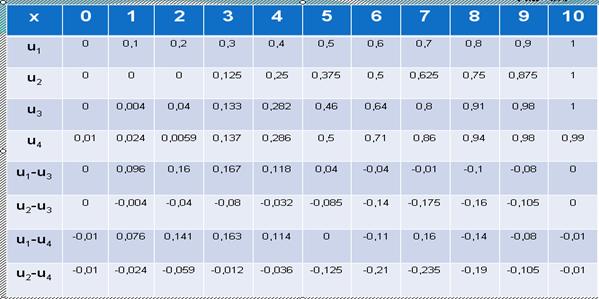
Observatii:
2.3 Corelatia simpla hiperbolica
In general, caracteristicile tehnice ale produselor sunt de doua tipuri:
a. Direct proportionale cu utilitatea (tip randament)
b. Invers proportionale cu utilitatea (tip consum specific
Pentru caracteristicile de tip "a" sunt valabile precizarile de pana acum
Pentru caracteristicile de tip "b" sunt necesare precizari suplimentare
Exista cel putin 2 variante de rezolvare a problemei
b1. Sa se gaseasca o forma de exprimare a dimensiunii tehnice, care sa creasca odata cu utilitatea: Se pot utiliza perceptele de la paragrafele anterioare
b2. Sa se gaseasca o relatie directa intre utilitatea si caracteristica tehnica in forma initiala: Exista 2 posibilitati de rezolvare
b2.1 Corelatia liniara intre utilitate si dimensiunea tehnica
b2.2 Corelatia de tip hiperbolic intre utilitate si dimensiunea tehnica
b2.1 Corelatia liniara intre utilitate si dimensiunea tehnica
Se considera dreapta (cu panta negativa) intre xmin si xmax de forma data in relatia
![]()
Cu conditia limita: u (xmin) = 1, care conduce la valoarea parametrului , conform relatiei
![]()
Rezulta in final expresia utilitatii, data in relatia
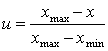
b2.2 Corelatia de tip hiperbolic intre utilitate si dimensiunea tehnica
Se considera relatia![]()
Cu conditia limita: u (xmax) = 0 si u (xmin) = 1, rezulta expresia utilitatii, conform relatiei
![]()
Exemplu
Se considera functia: "asigura precizie" (de masurare, de prelucrare etc.)
Caracteristica tehnica prin care se apreciaza utilitatea este "eroarea de masura" - (in procente din rezultatul exact)
Se poate, in opozitie, sa se utilizeze drept caracteristica tehnica , "gradul de precizie" - g (in procente din rezultatul exact)
Evident, intre cele doua marimi exista relatia:
![]()
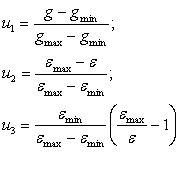 Folosind aceste caracteristici,
utilitatea se exprima cu relatiile:
Folosind aceste caracteristici,
utilitatea se exprima cu relatiile:
In tabelul 4, sunt prezentate valorile comparative pentru exemplul in care:
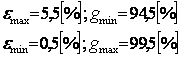
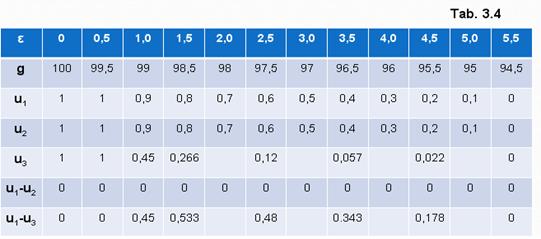
In figura 3, sunt prezentate cele trei expresii ale utilitatii :
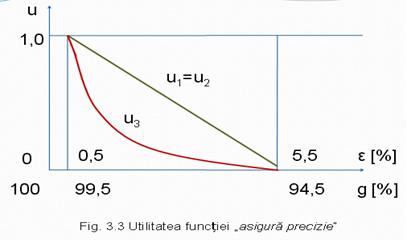
Concluzii:
- Primele doua functii sunt identice, ceea ce conduce la concluzia ca in cazul corelatieie liniare nu este necesar sa existe proportionalitate directa intre utilitate si dimensiunea tehnica
Daca se foloseste proportionalitatea prin originea axelor, concluzia ramane valabila
- Se constata o diferenta foarte mare intre valorile utilitatii pe dreapta respectiv hiperbola. Exista de fapt doua situatii distincte
2.4 Utilitatea functiei - corelatie multipla de dimensiuni tehnice
Desi functia a fost definita ca o caracteristica elementara - ceea ce presupune descompunerea pana in cele mai mici detalii a enunturilor - nu toate functiile pot fi apreciate printr-o singura caracteristica tehnica
In general, pentru a stabili legatura dintre utilitatea functiei si dimensiunile caracteristicilor tehnice care o determina, se poate utiliza o corelatie multipla
Avand in vedere dificultatea analizei, impusa de numarul de dimensiuni, se considera ca este suficient de buna aproximarea utilitatii cu ajutorul corelatiei liniare
Exista cel putin 2 situatii in care o functie trebuie sa fie specificata prin mai multe caracteristici tehnice:
Exemplul 1: Cazul dimensiunii tehnice "interval"
Se considera functia: "rezista la temperatura" care are dimensiunea tehnica exprimata printr-un interval de temperatura (care are o anumita marime dar si o anumita pozitie pe scara de temperaturi)
Nu este acelasi lucru sa "reziste" la intervalul (+20C +100C) sau (-20C +60C), cu toate ca cele doua intervale sunt egale, nefiind plasate in acelasi loc pe scara temperaturilor, au semnificatie diferita pentru utilizator
Pentru functia: "rezista la temperatura", se constata ca utilitatea acesteia creste odata cu cresterea intervalului de temperatura si cu cat fiecare limita de temperatura (minima si maxima) este mai departe de temperatura ambianta
Fie o expresie liniara de forma data in relatia
![]()
unde: T, t - reprezinta limitele maxima respectiv minima de temperatura;
a, b, c - reprezinta parametrii curbei
Prelucrand relatia (23), se obtine relatia
![]()
sau sub forma din relatia (25), deci o relatie dublu liniara
![]()
Conditiile limita pentru determinarea parametrilor si
Pentru T = Tmax si t = tmin u = 1
Pentru Tmin si t = tmax u = 0
Inlocuind in relatia (25) si rezolvand sistemul se obtine:
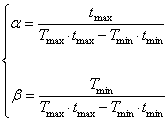
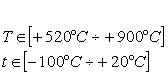 In figura 4 se prezinta rezultatul grafic
pentru functia: "rezista
la temperatura", pentru urmatoarele date:
In figura 4 se prezinta rezultatul grafic
pentru functia: "rezista
la temperatura", pentru urmatoarele date:
![]()
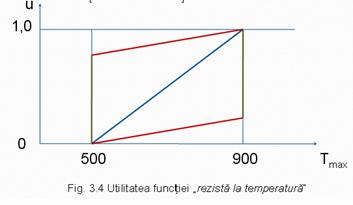
Concluzii:
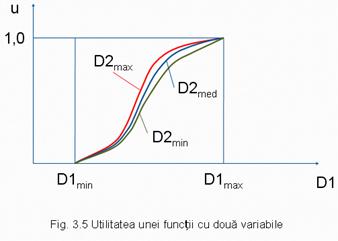
Exemplul 2: Cazul mai multor factori care definesc fenomenul
Se considera functia: "rezista la zdruncinaturi" care poate fi apreciata prin: marimea, numarul, frecventa si acceleratia zdruncinaturilor.
Nu pot fi delimitate functii care sa fie apreciate fie in raport cu marimea zdruncinaturilor, fie prin numarul sau frecventa de producere a lor. Trebuie luate in considerare toate acesta elemente simultan
Pornind de la performantele la care raspunde un aparat oarecare: durata socului - 10 ms, acceleratia maxima - 3g, numarul socurilor - 1000, frecventa - 1Hz, se simuleaza urmatoarea situatie:
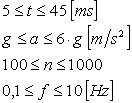
Durata zdruncinaturii
Acceleratia zdruncinaturii
Numarul de zdruncinaturi
Frecventa zdruncinaturii
Se constata ca toate dimensiunile tehnice sunt direct proportionale cu utilitatea functiei, pentru aprecierea functiei putandu-se folosi o corelatie cvadrupla liniara, conform relatiei
![]()
Pentru determinarea parametrilor, se considera ca cei patru factori influenteaza in mod aproximativ egal (cu 0,25) utilitatea functiei, rezultand expresia utilitatii din relatia
![]()
In capetele intervalului, rezulta pentru utilitate valorile:
![]()
aproximarea fiind suficient de buna
Generalizare
Daca utilitatea unei functii este determinata de mai multi parametri sau caracteristici tehnice, cu unitati de masura diferite si independente intre ele, pentru determinarea utilitatii intrinseci a functiei unei variante constructive se poate utiliza relatia
![]()
unde: di - dimensiunea concreta a caracteristicii tehnice
αi - coeficientul sau factorul de proportionalitate, determinat din conditiile limita
Observatii:
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 5038
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved