PREZENTAREA ALGORITMULUI DE ALOCARE SI NIVELARE A RESURSELOR

PREZENTAREA ALGORITMULUI DE ALOCARE SI NIVELARE A RESURSELOR

Stabilirea si esalonarea necesarului de resurse in cadrul productiei de serie se rezolva in ceea ce priveste resursa "utilaje" prin insasi structura algoritmilor - conditia de neinterferenta. Resursele "materiale" si "manopera" nu au in acest caz o pondere deosebita, ele putandu-se considera asigurate prin stocare si mijloace organizatorice.

Cu totul altfel se pune insa problema in lucrarile tip "unicat" (investitii, lucrari de constructii-montaj, reparatiile unor linii tehnologice, fabricarea unor agregate mari etc.) pentru care problema ordonantarii se rezolva cu ajutorul metodelor de analiza a drumului critic.

O succesiune de operatii se va reprezenta printr-un graf (retea) in care arcele vor reprezenta activitati (operatii) iar nodurile - evenimente (inceputuri sau terminari de activitati).

Situatia I

Se considera urmatoarea situatie:

resursele Ri nu trebuie sa depaseasca un anumit prag Qimax (i=1,.,s) al intensitatii consumului de resurse (alocarea resurselor).

termenele de predare sunt libere, deci nu se dau termene impuse.

intensitatea consumului de resurse se considera constant pe o anumita perioada de timp (ora, zi, saptamana, decada etc.).

In aceste conditii, sistemul de restrictii este:

t_{α , j+Δ} ≥ t_ωj , j = 1,.,n

k = 1,.,2n

unde indicele α arata termenul de incepere, ω - termenul de terminare, iar Δ este diferenta de numar de ordine dintre doua activitati precedente (admitand o numerotare sectventiala).

Conditia de optimalitate se exprima prin minimizarea celui mai mare termen de terminare t_ωh:

Aceasta este problema de alocare, cu termene libere.

Deoarece in aceasta problema intervine un numar mare de variabile si restrictii (de ordinal miilor), se foloseste un algoritm euristic de rezolvare.

Pasul 1. Se efectueaza analiza timpului, folosind algoritmul termenelor evenimentelor. Potrivit acestui algoritm, termenele minime ale evenimentelor sunt:

  (h , i) Є G,

unde s-a notat:

= termenul minim al evenimentului i;

A = multimea activitatilor;

A_hi = o activitate intre doua evenimente succesive E_h si E_i;

d_hi = durata activitatii A_hi;

G = graful activitatilor.

Termenele maxime ale evenimentelor sunt:

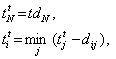(i , j) Є G,

in care t^t_i este termenul maxim al unui eveniment j.

Pasul 2. Se porneste de la momentul t^d₀ = 0. Se considera multimea A₀ a activitatilor A₀₁,., A_0n care pot incepe la momentul t₀^d. Fie d₀₁,., d_0n duratele acestor activitati. Fie intensitatile corespunzatoare activitatii A₀₁, intensitatile activitatii A_0n.

Pentru o resursa oarecare R_h se efectueaza diferenta:

h = 1,.,s,

unde k este numarul de activitati amanate (la inceput k = 0).

Exista doua posibilitati:

a) , pentru orice resursa R_h. In acest caz toate activitatile se plaseaza la termenul de incepere t⁰_d;

b) Exista o resursa R_h pentru care . In acest caz se calculeaza rezervele de timp R^k_i:

R^k_i = t_i^t - d_0i si se alege . Daca exista mai multe maxime, se alege activitatea cu durata minima. Activitatea aleasa se amana.

Se calculeaza din nou si se testeaza conditia a). Daca din nou conditia nu este satisfacuta, se amana o noua activitate cu rezerva maxima. Algoritmul se reia pana cand conditia a) este satisfacuta. Se obtine astfel o partitie a multimii A₀ in multimea activitatilor amanate si multimea activitatilor neamanate.

Pasul 3. Tuturor activitatilor amanate li se va modifica termenul minim de incepere. Termenul de amanare t^d₁ este:

unde prin d_0i^* s-au notat activitatile din multimea activitatilor neamanate. Se reia pasul 1, considerand t^d*₁ ca termen impus de incepere pentru activitatile amanate. Calculul se efectueaza numai pentru activitatile care nu au fost plasate.

Pasul 4.Se ordoneaza toate termenele minime de incepere ale activitatilor, inclusiv t^d*₁ si se considera minimul termenelor minime t^d_i. Fie t^d₁ acest nou termen. Se inlocuieste in pasul 1 t^d₀ prin t^d₁ si se reia algoritmul pana cand se plaseaza toate activitatile.

Situatia II

In conditiile enuntate mai sus, se cere respectarea unor termene impuse, intermediare sau finale (Th) (Termenele impuse se considera mai mari sau cel putin egale cu termenele care ar rezulta considerand resursele nelimitate). Cel mai frecvent se impune respectarea termenului final. In aceste conditii se aplica algoritmul euristic prezentat mai sus. Daca termenele nu se depasesc, problema este posibila, iar solutia gasita corespunde nevoilor practice. In caz de depasire a termenelor problema este imposibila (fara solutie).

Situatia III

Tot in conditiile enuntate mai sus se dau resursele suplimentare ΔQ. Aceste resurse pot fi folosite la suplimentarea pragului resursei R, numai in cazul in care se depasesc termenele impuse. Etapele de calcul sunt urmatoarele:

Pasul 1.Se aplica algoritmul prezentat mai sus. Daca in urma efectuarii acestor calcule se constata ca se respecta toate termenele impuse, solutia obtinuta este cea cauta. In caz contrar se trece la pasul 2.

Pasul 2. Se calculeaza noul prag al resurselor:

Q^*_imax = Q_imax + ΔQ_i

si se aplica din nou algoritmul prezentat. Deoarece resursele sunt mai mari, termenele sunt mai mici decat in cazul fara resurse suplimentare. Daca noile termene ale evenimentelor nu depasesc termenele impuse, problema este rezolvata. Daca se depaseste cel putin un termen impus, problema este imposibila.

Situatia IV

In acest caz se dau duratele suplimentare ΔTh cu care pot fi depasite termenele impuse in caz de necesitate. Etapele de calcul sunt:

Pasul 1.Se aplica algoritmul ca in situatia I. Daca se respecta toate termenele impuse, problema este rezolvata, iar daca nu, se trece la pasul 2.

Pasul 2. Se calculeaza noile termene impuse

T^*_h = T_h + ΔT_h

si se reia algoritmul. In cazul cand nu se depasesc noile termene impuse, problema este rezolvata. In caz contrar, problema este imposibila.

Situatia V

In conditiile prezentate in situatia I se dau atat marimile resurselor suplimentare ΔQ, care pot fi folosite la suplimentarea pragului Q_imax al resursei R cat si un supliment de timp ΔT cu care se poate mari, in cazuri exceptionale, termenul final impus T. De asemenea, se cunosc costurile de penalizare P pentru depasirea cu o unitate a pragului Q_imax al resursei R si costul de penalizare C pentru depasirea cu o unitate a termenului impus T. Se mai cunoaste beneficiul B pentru predarea lucrarii cu o unitate de timp inainte de termenul impus T. Se cere solutia care conduce la cost suplimentar minim. Obiectivul propus este de a minimiza suma cheltuielilor rezultand din depasirea duratei impuse si a disponibilului de resurse, ceea ce ar echivala cu conditia minimizarii expresiei:

, in care ΔQ^e_ij este depasirea efectiva a pragului Q_imax corespunzator resursei R pe un interval de durata d_ij, in care intensitatea cumulata a consumului resursei R este constanta;

d_ij este durata intervalului in care intensitatea cumulata a consumului resursei R are o marime constanta Q_ij^e;

v reprezinta numarul de intervale de timp in care intensitatea cumulate a consumului resursei este constanta si este mai mare decat pragul resursei R, adica Q^e_ij > Q_imax;

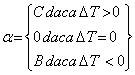
Pentru a rezolva aceasta problema de minimizare a costului se poate utiliza un algoritm euristic ale carui etape de calcul sunt:

Pasul 1.Se aplica algoritmul prezentat pentru rezolvarea situatiei I (de la pasul 1 pana la pasul 4 inclusiv), netinand seama de termenele impuse si considerand ca pragul fiecarei resurse este Q_imx. In urma acestui calcul rezulta un termen final efectiv T⁰. Daca termenul final este mai mic decat termenul impus, problema este rezolvata. Daca termenul final este mai mare decat termenul impus, se calculeaza cheltuielile ΔF₀ in ipoteza folosirii unor resurse care nu depasesc pragul Q_imx, conform relatiei:

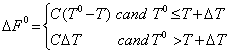
Se trece apoi la pasul 2.

Pasul 2.Se mareste pragul resurselor de la Q_imax la Q_imax + ΔQ si se aplica din nou algoritmul prezentat pentru rezolvarea situatiei I. Se obtin marimile efective ale resurselor Q¹_ij, care satisfac relatia Q¹_ij ≤ Q_imax + ΔQ si termenul efectiv T¹ care satisface relatia T¹ ≤ T⁰.

Daca T¹ > T + ΔT, problema este imposibila, iar algoritmul se opreste la acest pas. Daca T¹ ≤ T + ΔT, se calculeaza costul suplimentar ΔF¹ in ipoteza folosirii unor resurse care nu depasesc Q_imax + ΔQ. Se obtine expresia:

ΔF¹ =   in care

Q¹_ij = max [(Q¹_ij - Q_imax ) , 0],

ΔT¹ = T¹ - T,

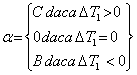
-d¹_ij este durata intervalului pentru care marimea intensitatii cumulate a resursei R este Q_imax + ΔQ¹_ij

Pasul 3.Se aplica metoda injumatatirii intervalului.

In acest caz se calculeaza:

-jumatatea intervalului [T , T +ΔT]:

T₁^* = (T₁ + T + ΔT) / 2

-termenul suplimentar al marimii T₁^* calculate fata de termenul efectiv T₁ adica:

δT₁ = T₁^{* -} T₁

-coeficientul adimensional β care exprima cota parte din suplimentul ΔQ al resursei R care asigura, cu o oarecare aproximatie, realizarea tuturor activitatilor in termenul T₁^*:

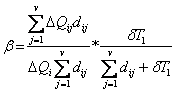
Rezulta o noua marime a pragului resursei

Q¹_imax = Q_imax + βΔQ

Considerand Q¹_imax noile limite ale resurselor, se reia algoritmul de la pasul 3 pana cand diferenta Tⁿ - T^n-1 devine egala cu unitatea de masura a timpului luata in consideratie. Termenul minim al secventei reprezinta valoarea optima a cheltuielilor, iar termenul efectiv corespunzator, precum si limitele corespunzatoare ale resurselor constituie strategia optima.

Situatia VI

In conditiile situatiei I se cere sa se uniformizeze consumul tuturor resurselor. Problema este deosebit de dificila, deoarece este posibil ca optimul pentru o resursa sa constituie o solutie dezavantajoasa: daca incercam sa imbunatatim situatia prin glisare (amanare) pentru o resursa R, este posibil ca la alta resursa sa se obtina neuniformitati exagerat de mari. Pentru a rezolva aceasta problema este posibila utilizarea mai multor criterii de optimizare, din punct de vedere al uniformitatii in conditiile unui numar oarecare de resurse.

Pentru aceasta se foloseste notiunea de profil al unei resurse. Daca programul are n activitati, iar h este variatia intensitatii consumului resursei j la activitatea i (reducere sau crestere), profilul H este dat de vectorul

Hj = (h_1j,.,h_nj)

Un prim criteriu de optimalitate este minimizarea variatiilor intensitatii resursei, ceea ce echivaleaza cu minimizarea expresiei

Un alt criteriu de optimalitate este considera variatiile relative ale resurselor, ponderandu-le dupa importanta economica, ceea ce revine la minimizarea expresiei

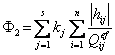
in care Q^ef_ij este intensitatea efectiva a resursei j pentru activitatea de rang i, iar k_j este coeficient de ponderare economica a resursei.

Un alt criteriu care se poate propune este minimizarea sumei ponderate a diferentelor maxime dintre intensitatea medie Qmed a aceleiasi resurse R.Algoritmul euristic bazat pe acest criteriu este urmatorul:

-expresia cantitativa a criteriului de minimizare enuntat mai sus este

Pentru a minimiza aceasta functie se procedeaza astfel:

Pasul 1.Se calculeaza intensitatea medie a resurselor R:

Qmed1,.,Qmeds

Pentru fiecare resursa R se considera un prag Qp₁ calculat cu ajutorul relatiei:

Qp = ρ₁ Qmed

in care ρ este un coeficient supraunitar. Resursa suplimentara este ΔQp₁ = (ρ₁ - 1)Qmed. Daca aplicand algoritmul de la situatia III se constata ca problema este posibila, solutia este marirea intensitatii resursei pana la pragul Qp. Daca problema nu este posibila, se trece la pasul 2.

Pasul 2. La resursele care au provocat depasirea termenului impus se mareste ρ₁. Fie R aceste resurse. Atunci se ia

Qp₂ = ρ₂ Qmed , unde ρ₂ > ρ₁

Resursa suplimentara este ΔQp₂ = (ρ₂ - 1)Qmed. Din nou se aplica algoritmul de alocare prezentat la situatia III. Daca intensitatea Qp₂ a resursei R asigura realizarea lucrarilor la termen, calculul se incheie. Daca nu, se reia algoritmul de la pasul 2. Calculul se opreste atunci cand la toate resursele s-au stabilit limitele care asigura realizarea lucrarilor in termenul impus.

Algoritmul presupune inceperea calculelor prin utilizarea coeficientilor ρ₁,., ρ_n. Alegerea acestor coeficienti trebuie sa fie astfel conceputa incat functia de eficienta Ф₃ sa tinda catre o valoare apropiata de zero. Acest mod de initializare este avantajos, deoarece evita variatii exagerate ale resurselor. La resursele mai putin importante, coeficientii vor avea cresteri mai rapide, iar la resursele mai importante, mai lente.

Pentru uniformizarea resurselor se poate folosi programul PERT-Resurse.