Practica controlului statistic al proceselor de fabricatie

Practica controlului statistic al proceselor de fabricatie

1. Limitele de control si de supraveghere

2. Controlul statistic prin masurare

3. Controlul statistic prin atribute

4. Controlul prin numar de defecte

3. Controlul statistic prin atribute

Exista caracteristici ale produselor care sunt greu masurabile sau nemasurabile. In urma examinarii lor, de cele mai multe ori vizual, produsele se clasifica direct in corespunzatoare si necorespunzatoare.

Si in cadrul caracteristicilor atributive se pune problema gasirii unor metode pe baza carora sa se poata decide daca procesul se desfasoara normal. Este necesar sa se stabileasca numarul maxim de unitati necorespunzatoare pe care le pot contine o proba de marime n, pentru a considera ca procentul de rebuturi efectiv nu depaseste procentul admis.

Se recomanda ca numarul unitatilor care compun proba sa fie mai mare (de regula intre 20 si 60), pentru a sesiza variatiile mici ale procentului de rebut real, determinate de aparitia unei cauze perturbatoare sistematice.

Daca procesul de fabricatie este supus unei variatii rapide care pot conduce la aparitia rebuturilor, se impune extragerea mai frecventa a probelor. In acest caz, marimea probei poate fi mai mica.

Se recomanda ca la stabilirea marimii probei sa se ia in considerare pierderile care apar in urma formularii unor decizii necorespunzatoare.

Controlul statistic prin atribuire se poate efectua sub forma:

-controlul procentului de produse necorespunzatoare;

-controlul numarului de produse necorespunzatoare.

3.1. Controlul procentului de produse necorespunzatoare (fisa p)

Daca fractiunea defectiva specifica procesului de fabricatie ramane constanta, atunci procentul de produse necorespunzatoare al fiecarei probe va varia de la proba la proba sub forma unei repartitii binomiale cu parametrii:

-media = fractiunea defectiva p₀ sau;

-abaterea standard= sau

Ipoteza nula care urmeaza sa o testam cu acest prilej este:

H₀:p£p₀

Cu alternativa:

H₁:p=p>p₀

unde p₀ este fractiunea defectiva admisa, iar p -fractiunea defectiva reala a procesului (posibila).

Numarul produselor necorespunzatoare poate fi 0, 1, 2, ., n, rezulta ca se poate obtine cu una din relatiile:

.

Abaterea medie patratica a procentului de produse necorespunzatoare s_p se obtine cu relatia:

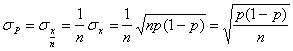
Aceasta marime este o fractiune a volumului esantionului.

Repartitia se poate aproxima cu cea normala daca np>10 sau daca n p(1-p)³9. Acest lucru ne permite sa folosim in continuare variabila normala normata z.

La efectuarea controlului se va determina numai limita superioara, caz in care se identifica doua situatii:

a. procentul de produse necorespunzatoare este cunoscut si estimat, pornind de la rezultatele inregistrate in fabricatiile precedente. In aceasta situatie limita de control se calculeaza pornind de ;la procentul de produse necorespunzatoare admis p₀, sau fractiunea defectiva admisa, la care vom adauga de z_a ori abaterea medie patratica a fractiunii defective admise, adica:

Aceasta limita se traseaza pe fisa de control statistic, denumita simbolic "fisa p" fig. 1.

b. Procentul de produse necorespunzatoare este necunoscut. In aceasta situatie valoarea p₀ se estimeaza cu (procentul mediu de produse necorespunzatoare), obtinut in urma analizei premergatoare a procesului de fabricatie. Din productia masinii se extrag aproximativ 25 probe de cate 20-60 exemplare. Daca in proba i s-au gasit d_i exemplare necorespunzatoare, numarul mediu de exemplare necorespunzatoare gasite in cele v probe examinate (fiecare de marimea n) se calculeaza cu relatia:

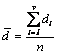
Procentul mediu de produse necorespunzatoare este:

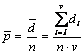, daca numarul de exemplare din proba este constant, sau

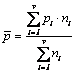, daca numarul exemplarelor in proba variaza.

Se precizeaza ca in situatia cand determinarea lui nu se poate face in prealabil, se alege la inceput o valoare arbitrara a fractiunii defective admisibile. Apoi, in cursul aplicarii se recurg la datele care permit estimarea lui .

Limita de control se calculeaza cu relatia:

, in cazul in care marimea probei n este cunoscuta, sau cu relatia:

, in cazul in care marimea probei poate lua valori diferite n₁¹n₂¹ ¹n_i. In aceasta situatie, pe fisa de control se traseaza cate o limita de control pentru fiecare marime a probei.

Literatura de specialitate indica pentru factorul z_a valoarea 3, care corespunde unui risc de genul I de 0,28% (adica la 1000 de probe examinate, se admit aproximativ trei interventii inutile). In acest caz limita de control va deveni:

.

Controlul se aplica astfel: din productia masinii se extrag probe de marimea n si se calculeaza pentru fiecare procentul de produse necorespunzatoare p, intalnindu-se doua situatii:

-daca p£LCS, aceasta inseamna ca procentul de produse necorespunzatoare efectiv nu s-a modificat, adica masina lucreaza corespunzator;

-daca p³LCS, inseamna ca masina nu mai lucreaza cu procentul normal. Se opreste, se depisteaza cauza care a perturbat sistemul si se inlatura.

Aplicatia nr. 1

Propunem introducerea controlului statistic pe baza" fisei p" la produsul A realizat de o masina. In acest scopn s-au realizat, timp de 30 de zile, culegeri de esantioanezilnice de marimea a 100 bucati. Rezultatele controlului sunt prezentate in tabelul urmator

Intrucat nu se cunoaste fractiunea defectiva si dispersia caracteristicii procesului de fabricatie, pentru calculul limitei de control se vor utiliza relatiile prezentate la cazul b. Se determina fractiunea defectiva medie cu relatia

Se considera mai intai p=, iar z_0,0612=1,84

Aplicand relatia in care z_a=3 rezulta

Pentru siguranta deciziei, avand in vedere ca procesul de fabricatie are o fractiune defectiva mare(), se recomanda sa se lucreze cu prima limita de control, respectiv cu LC(p)=0,047

3.2. Controlul numarului de produse necorespunzatoare (fisa np)

In cazul cand verificarea calitatii produselor se face la "corespunzator" si "necorespunzator", controlul statistic se poate efectua si prin numarul de produse necorespunzatoare d_i gasite in proba examinata, sau prin asa numita fisa np.

Se cunoaste ca numarul de probe necorespunzatoare continut intr-o proba de marime n are o repartitie binomial cu media np si dispersia np(1-p).

In baza algoritmului de la punctul 3.1 rezulta ca limita de control se calculeaza cu relatiile:

, daca se cunoaste fractiunea defectiva p₀ specifica procesului, sau cu relatia:

In cazul controlul numarului de produse necorespunzatoare rezulta:

Daca pentru z_a se ia valoarea 3, limita de control va fi:

, in cazul in care

Limita de control determinata cu una din formulele prezentate se traseaza pe fisa de control statistic respectiv pe fisa np.

Fisele p si np specifice controlului statistic prin atribute prezinta atat avantaje, cat si dezavantaje in comparatie cu fisele de control statistic prin masurari.

Avantaje:

-necesita calcule putin voluminoase:

-costurile cu aplicarea lor sunt mai reduse.

Dezavantaje:

-nu sunt asa de sensibile ca fisele de control prin masurare;

-au o precizie mai redusa datorita pierderilor de informatii pe care le genereaz

Aplicatia nr. 2

Propunem ca in situatia prezentata in aplicatia nr. 1 controlul statistic al calitatii sa se faca pe baza numarului de produse necorespunzatoare in proba, atunci limita de control superioara se calculeaza cu relatia:

Controlul prin numar de defecte

Controlul static pe baza de numar de defecte se foloseste atunci cand:

a. defectele de un singur fel (dupa o anumita caracteristica a calitatii) sau defectele de mai multe feluri (dupa mai multe caracteristici) pe exemplar apar relativ frecvent;

b. defectele de un singur fel sau defectele de mai multe feluri, in proba au o aparitie relativ frecventa.

In primul caz se foloseste fisa de control U, iar in al doilea caz - fisa de control C.

Prin cele doua fise de control se urmaresc numai defectele independente. In cazul in care unele defecte sunt legate cu altele si le conditioneaza, acestea din urma nu se mai numara ca atare. Daca defectele difera intre ele mult ca importanta, acestea se insumeaza numai dupa ce in prealabil, li s-au aplicat anumiti coeficienti de ponderare, dupa importanta lor.

Identificarea defectelor se face prin examinarea vizuala, prin masurare, prin incercari mecanice sau electrice, prin analize chimice, etc. Produsul controlat care contine unul sau mai multe defecte pe baza carora este declarat necorespunzator prescriptiei de calitate, se numeste produs defect (sau defectiv).

Controlul prin numar de defecte se recomanda atunci cand probabilitatea aparitiei unui numar mare de diferite feluri de defecte este mica, asa cum este cazul de exemplu la produse ca: tesaturi, televizoare, incaltaminte, etc.

Legea de repartitie a variabilei numar de defecte este Poisson, cu parametri: media=dispersia = l . Putem spune ca in cazul numarului de defecte avem de testat ipoteza nula:

H₀ : l l

cu alternativa

H₁ : l l (l > l

Dupa unii autori cand l ³ 5, dupa alti autori cand l ³ 9, repartitia Poisson se poate aproxima prin cea normala normata:

Fisa U de control se foloseste pentru depistarea defectelor pe exemplar (pe unitate). De obicei, se foloseste cand marimea probei n nu se mentine constanta.

Pentru intocmirea fisei de control se face analiza premergatoare a procesului de fabricatie. Se extrag din productia masinii, dupa regulile descrise in paragrafele precedente, un numar de k probe (circa 25) de marime n. Se numara apoi pe fiecare proba de cate ori apar defectele urmarite. Numarul defectelor in proba se noteaza cu C. Se calculeaza numarul defectelor pe exemplar pentru fiecare proba, dupa relatia:

.

Daca marimea probei n este constanta, numarul mediu al defectelor pe exemplar pentru toate cele k probe se obtine cu relatia:

,

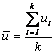in care u_i este numarul de defecte pe exemplar pentru proba i (i = 1, 2, ., k).

Limitele de control se calculeaza cu relatiile:

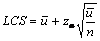si .

Daca marimea probelor variaza, fiind n₁, n₂, ., k, numarul mediu al defectelor pe exemplar pentru cele k probe cercetate se calculeaza cu relatia:

,

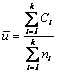unde C_i este numarul defectelor din a i-a proba de marime n_i .

In acest caz limitele de control se obtin cu relatiile:

si .

Daca din cercetari anterioare se cunoaste numarul de defecte pe exemplar sau daca el este stabilit a priori - U₀ , limitele de control se vor determina asemanator, cu deosebirea ca in loc de se trece valoarea U₀. In practica se mai foloseste pentru factorul z_a, valoarea 3, respectiv regula trei sigma, adica:

sau

.

Controlul defectelor pe exemplar se efectueaza conform prescriptiilor STAS 5997-72, cu ajutorul fisei de control prezentate in acest standard.

Fisa C de control se foloseste pentru depistarea defectelor din proba. Se utilizeaza indeosebi atunci cand marimea probei n se mentine constanta sau atunci cand produsul nu se prezinta sub forma de unitati naturale distincte.

In cazul marimii constante a probei n, pe baza celor k probe examinate in cadrul analizei premergatoare a procesului de fabricatie se calculeaza numarul mediu al defectelor din proba cu relatia:

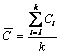
unde C_i este numarul defectelor din proba i.

Pentru calcularea limitelor de control folosim relatiile:

si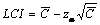

In practica, pentru factorul z_a se iau, de regula, doua valori: 1,96 si 3. Se obtin astfel:

-limitele de supraveghere =si

-limitele de control=

Aplicatie. Pentru introducerea controlului statistic pentru determinarea defectelor de fabricatie la un produs (diskete) s-a realizat o cercetare in prealabil. In acest scop s-au extras din productia procesului de productie 10 esantioane, fiecare avand volumul de 5 bucati. Dupa efectuarea controlului a rezultat situatia din tabelul urmator:

Se determina numarul mediu al defectelor din proba pentru toate cele 10 esantioaneastfel:

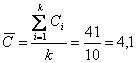defecte

Se va atribui lui z_a=3. Limitele de control vor fi in acest caz:

<0

Controlul se desfasura astfel: la intervale de timp precizate se extrag din productia procesului tehnologic cate un esantion format din 5 diskete. Daca numarul de defecte din esantion nu depaseste LCS =10 defecte, se considera ca procesul se desfasoara normal.

Sa consideram ca se doreste sa se stabileasca limitele de control pentru numarul mediu de defecte pe unitate sau pe exemplar. In acest caz se determina numarul mediu de defecte pe unitate

Consideram z_a=3, limitelr de control pentru fisa U vor fi:

<0 LCS=0

valori care se trec pe fisa de control

Controlul se va desfasura astfel: la intervale de timp precizate se extrage din productia procesului de productie cate un exemplar pentru care se stabileste numarul de defecte u_i. Daca u_i £LCS=2 se considera ca procesul se desfasoara normal, iar daca u_i>LCS=2 se desfasoara anormal