| CATEGORII DOCUMENTE |
| Comunicare | Marketing | Protectia muncii | Resurse umane |
Studiul pietelor oligopoliste utilizand teoria jocurilor
In conditiile in care rezultatul deciziilor unei firme depinde semnificativ de deciziile luate de una sau mai multe firme (identificabile), atunci avem situatia de piata denumita oligopol. In mod obisnuit, oligopolul e definit ca o piata cu cativa vanzatori (acesta e si intelesul termenului de oligopol, prin constructia sa); insa o definire avand la baza numarul firmelor de pe o piata nu e lipsita de ambiguitate. Din moment ce esenta acestei situatii este data de natura relatiilor competitionale dintre vanzatori, e normal (e cel mai bine) ca aceasta sa fie baza definitiei. Oricum, intuitiv, intotdeauna ne gandim la oligopol ca la o "competitie intre cativa".
Consideram ca o firma, in aceste conditii de interdependenta a procesului decizional, va cauta sa-si maximizeze profitul. Problema ce apare e sa atribuie un profit fiecarei decizii alternative, cu scopul de a le ierarhiza si de a gasi optimul. Vrand-nevrand, fiecare firma e implicata intr-un rationament de tipul: "daca eu aleg A si el alege B, atunci castig x; daca eu aleg C si el alege D, atunci castig y, .", s.a.m.d. Relatiile competitorului (aici B, D) pot lua un numar de firme, astfel ca firma in cauza trebuie sa-si dea seama care va fi raspunsul. Inainte de ierarhizarea alternativelor, firma va trebui sa analizeze fiecare actiune posibila a competitorilor. Teoria oligopolului se ocupa cu intelegerea si previzionarea deciziilor competitorilor, in astfel de destinatii de stransa interdependenta strategica (adica interactiuni in gandirea si procesul decizional al firmelor de pe piata).
Un mod natural de analiza pare a fi formularea unor ipoteze asupra naturii reactiilor competitive asteptate de fiecare firma si folosirea lor pentru gasirea unei situatii de echilibru. Utilizand apoi instrumentele de baza ale analizei microeconomice se ajunge la o precisa determinare a echilibrului pietei. Aceasta abordare a fost intr-adevar una din primele adoptate de economisti. Exista cateva ipoteze asupra modelelor de reactii care sunt posibile, fiecare ducand la solutii de echilibru diferite. Vom avea atunci cateva teorii posibile, cu solutii diferite. Acesta nu trebuie sa fie o ingrijorare: evidenta empirica face diferenta intre diferitele ipoteze, rezultand cea mai potrivita ipoteza pentru orice situatie concreta.
Aplicarea teoriei firmelor in analiza oligopulului a dus la reinterpretari fundamentale ale acestor modele. Abordarea prin teoria jocurilor nu permite alegerea unui model de reactie arbitrar, chiar daca e plauzibil. Mai mult, asteptarile asupra actiunilor unui competitor rezulta in urma unor calcule rationale ale firmei in cauza. Totusi modelele traditionale de oligopol pastreaza un loc central in teoria oligopolista; completarea adusa de analiza concreta (din teoria jocurilor) a dus la o definire mai atenta a tipurilor de piata in care se pozitioneaza firmele si a dus chiar la o mai adanca intelegere a modelelor in sine.
Se pune acum problema posibilitatii de comunicare si cooperare intre firme. Citam un pasaj din Adam Smith: "Oamenii din acelasi comert se intalnesc uneori, chiar si pentru a petrece, dar conversatia de termina cu o conspiratie impotriva consumatorilor sau prin gasirea unui mecanism de crestere a preturilor. E imposibil de prevenit astfel de intalniri, prin nici o lege care sa fie in concordanta cu justitia si cu respectarea libertatilor personale." Admitand posibilitatea comunicarii si cooperarii, se schimba unele aspecte ale analizei. In loc de a construi modele de reactie si examinarea consecintelor lor posibile, suntem interesati in a raspunde la intrebari ca:
In ce conditii firmele vor fi de acord sa coopereze?
Daca se decid sa coopereze, ce politic de pret si output vor rezulta?
Intelegerea lor comuna va fi stabila (in sensul mentinerii in timp, in circumstante schimbate) si daca nu, care vor fi consecintele incalcarii acordului?
Cooperarea intre firme (maximizarea de profit) depinde crucial de numarul de perioade in care situatia de piata se repeta. Modelele clasice de oligopol trateaza implicit situatia de piata ca un joc cu o singura mutare: firmele produc si vand o singura data. In acest caz se dovedeste a fi dificil de rationalizat comportamentul cooperativ. Daca, pe de alta parte, privim situatia ca pe un joc repetitiv (posibil cu un numar infinit de perioade) devine usor de explicat acest comportament cooperativ; dificultatea apare in stabilirea cu exactitate a preturilor si cantitatilor ce vor fi atrase.
In aceasta parte vom lucra in termenii unui model foarte specific. Avantajul consta in faptul ca rezultatele apar foarte simplu si foarte clar. Dezavantajul e acela ca nu intotdeauna e clar daca aceste rezultate se genereaza; probleme generale cum ar fi existenta, unicitatea sau stabilirea echilibrului nu sunt tratate.
Presupunem ca pe piata se confrunta doua firme, cu functia costului total:
![]() , ci > 0, i=1,2 [1]
, ci > 0, i=1,2 [1]
cu costurile marginale ci constante.
Output-urile firmelor pot fi omogene sau nu. (Daca sunt omogene ci=cr.) Functia cerere inversa pentru firma i:
![]() , i,j=1,2, i<>j [2]
, i,j=1,2, i<>j [2]
unde g>0
Bunurile sunt astfel substituite: o crestere a output-ului firmei j (ca urmare a scaderii pretului) coboara functiile cererii si venitului pentru firma i.
Presupunem ca ![]() ,
pentru ca piata sa fie activa.
,
pentru ca piata sa fie activa.
Daca output-urile sunt omogene,
![]()
![]() [3]
[3]
In conditii de omogenitate avem o singura functie a cererii
inverse: ![]() si
deci bunurile vor fi vandute la acelasi pret dat de suma output-urilor.
si
deci bunurile vor fi vandute la acelasi pret dat de suma output-urilor.
Functia profitului pentru cele doua firme:
![]() [4]
[4]
Functia cerere (din functia cererii inverse):
![]() [5]
[5]
Scriem astfel profitul ca functie de preturi:
![]() [6]
[6]
Din relatia [4] rezulta ca ![]() este strict concav in raport cu qi:
este strict concav in raport cu qi:
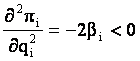 cu un maxim in
cu un maxim in 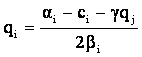 [7]
[7]
Functia ![]() este liniara si descrescatoare in qi:
este liniara si descrescatoare in qi:
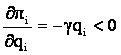 .
.
Aceasta situatie poate fi considerata ca un joc in forma normala G=(N,S,P) in care:
multimea jucatorilor este formata de cele doua firme de pe piata N=
spatiul strategiilor este ![]() ,
deci fiecare firma este libera sa produca orice cantitate nenegativa de output;
,
deci fiecare firma este libera sa produca orice cantitate nenegativa de output;
functiile de castig sunt reprezentate de functiile de profit ale celor doua firme date de relatia [4]: P=(p p
In paralel cu reprezentarea teoretica, vom face si o analiza numerica practica, studiind piata bauturilor racoritoare ambalate la 2 litri. Cele doua firme cu cea mai mare pondere pe piata romaneasca sunt Coca-Cola si European Drinks. Ne vom referi la Coca-Cola folosind termenul firma 1 si variabilele corespunzatoare vor avea indicele 1, iar European Drinks va fi firma 2, cu indicele pentru variabile 2.
Perioada de analiza este o luna.
Functiile de cost (exprimate in milioane lei)
C1=6q1 è c1=6
C2=5q2 è c2=5
Functiile de cerere inversa:
p1=18-0,01q1-0,005q2 è a b g
p2=14-0,008q2-0,005q1 è a b
Observatie: Cantitatile q1 si q2 sunt exprimate in mi sticle deci costurile marginale sunt exprimate in mii lei per sticla.
Modelul Cournot
Sa spunem ca piata functioneaza dupa cum urmeaza. Fiecare firma decide, fara a se consulta cu cealalta, ce output va produce. Simultan, firmele apar cu bunurile pe piata. Preturile se ajusteaza la nivelul ce curata piata, firmele luandu-si profitul rezultat. Intrebarea care se pune este ce nivel al output-ului vor produce.
Sa notam ca relatia [7] ofera firmelor o informatie foarte
importanta: fiind dat un nivel al output-ului qi al firmei
concurente j, cel mai bun raspuns al firmei i este dat de [7]: 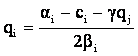 .
in conformitate cu aceasta, se defineste functia cel mai bun raspuns[1]
pentru firma i:
.
in conformitate cu aceasta, se defineste functia cel mai bun raspuns[1]
pentru firma i:
![]()
![]()
![]()
![]() [8]
[8]
cu
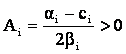 ;
; 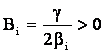 .
.
Pentru modelul numeric, aceste functii vor fi:
q1(q2)=600-0,25q2
q2(q1)=562,5-0,3125q1
Pantele negative ale acestor drepte (-Bi) explica faptul ca o crestere de output qj reduce cantitatea de output maximizatoare de profit a firmei i.
Punctul de intersectie al acestor drepte e dat de:
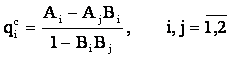 [9]
[9]
rezultat dat de rezolvarea sistemului de ecuatii definit de [8].
Deci q1c=500 (mii sticle)
q2c=400 (mii sticle)
Preturile la care se vor desface aceste cantitati vor fi:
p1c=18-5-2=11 (mii lei/sticla)
p1c=14-3,2-2,5=8,3 (mii lei/sticla)
Profiturile obtinute de cele doua firme sunt:
p c=11*500-6*500=2500 (milioane lei)
p c=8,3*400-5*400=1320 (milioane lei)
In conditii de omogenitate
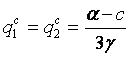 (Am folosit [3]) [10]
(Am folosit [3]) [10]
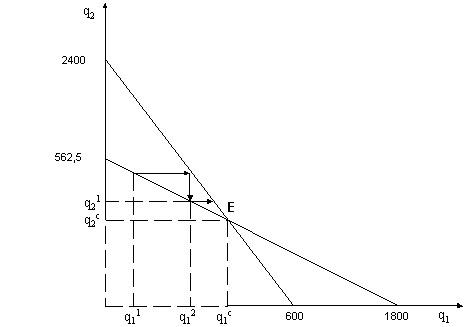
Figura 1 Modelul Cournot
functiile cel mai bun raspuns ale celor doua firme si punctul de echilibru E
ajustarea la echilibru
In analiza sa, Augustine Cournot propunea acest punct de intersectia E ca punct de echilibru al pietei. Argumentele sale urmareau rationamentul urmator: firma 1 apare pe piata cu q11; firma 2 reactioneaza cu output-ul maximizator de profit q21; in urma acestui raspuns, firma 1 isi va schimba output-ul in q12, care ii minimizeaza profitul, ., s.a.m.d. (figura 1). De vreme ce fiecare firma reactioneaza la output-ul celeilalte prin stabilirea output-ului propriu pe baza functiei cel mai bun raspuns ("curba de reactie" in terminologia lui Cournot), singurul echilibru posibil pe piata este punctul de intersectie E(q1c, q1c). Acesta este punctul in care nici una din firme nu doreste sa-si schimbe output-ul dat fiind output-ul firmei concurente.
Argumentul lui Cournot nu e convingator. Trebuie notata inconsistenta relativa la ipoteza jocului intr-o mutare de vreme ce stabilirea output-ului se face secvential, intr-un numar (posibil infinit) de perioade. Acest comportament e denumit de Bruce T. Allen "joc de preturi cu ochii inchisi" (Managerial Economics). Fiecare firma se asteapta ca cealalta sa-si pastreze constant output-ul; mai mult decat atat, aceasta convingere e pastrata in continuare, dupa ce se dovedeste (in fiecare perioada) ca e nerealista.
Abordarea moderna prin teoria jocurilor a acestui model nu furnizeaza un rationament realist, pentru acelasi output de echilibru. Se presupune ca fiecare firma actioneaza rational (lucru cat se poate de normal si de adevarat), socotind consecintele deciziilor sale pe baza faptului ca si cealalta firma actioneaza rational. In aceste conditii, output-urile produse de firme sunt considerate ca fiind un echilibru Nash.
Perechea output-ului (q1*, q2*) e un echilibru Nash, daca:
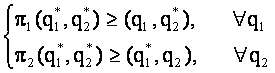 fezabile [11]
fezabile [11]
Evident ca (q1c, q1c) satisface aceasta definitie si, in plus, e singura astfel de pereche din model. Asadar, echilibrul Nash al acestui joc e echilibrul Cournot, de vreme ce e necesar sa fie la intersectia functiilor cel mai bun raspuns.
Argumentul ce sustine folosirea conceptului de echilibru Nash ca solutie a jocurilor de acest tip consta in urmatorul rationament. Presupunem ca firma 2 crede firma 1 va produce q11; atunci isi calculeaza cel mai bun raspuns q21 relativ la asteptarile sale. Insa realizeaza ca si firma 1 poate rationa similar: pentru un output asteptat q21, va dori sa produca q12. Ar fi irational din partea firmei 2 sa creada ca firma 1 va pastra nivelul q11. Acest rationament se face in fiecare punct, mai putin (q1c, q1c). Daca firma 2 crede ca firma 1 va alege q1c, ea va dori sa produca q2c. Firma 2 isi da seama ca cel mai bun raspuns al firmei 1 la alegerea q2c este tot q1c si deci nu va mai dori sa-si schimbe output-ul (e valabil si pentru firma 1).
Echilibrul Nash are proprietatea ca daca i stie ca j va alege qj*(=qjc) in conditiile in care i ar alege qi*(=qic)>i totusi nu va dori sa-si schimbe output-ul, ramanand la nivelul qi*.
Firmele ajung sa faca alegerea (q1*, q2*) in urma aceluiasi rationament. Un argument in sustinerea echilibrului Nash e acela ca orie punct care nu e un echilibru Nash nu va fi ales de un jucator convins ca oponentul sau e rational si la fel de bine informat.
Sa vedem in continuare ce s-ar intampla daca firmele coopereaza. In acest caz, avem de maximizat profitul comun:
![]() <==>
<==>
![]()
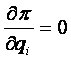 è
è ![]()
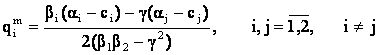
Se arata ca qim < qic.
Asadar, nivelul output-urilor e mai ridicat in preturile mai mici in cazul solutiei Cournot (concurentiale) decat in cazul cooperarii.
In cazul output-urilor omogene:
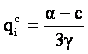 è
è 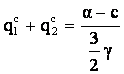
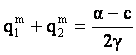
![]()
![]()
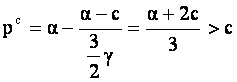 , (caci a>c)
, (caci a>c)

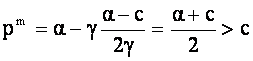
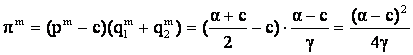
Evident ![]() .
.
Observatie:
Aceasta relatie se pastreaza si pentru output-uri diferentiate (neomogene).
Cazul cooperarii poate fi asemanat cu cazul de monopol (pe piata e un singur agent: cartelul format din cele 2 firme care coopereaza); de aici si notatiile pm, qm, pm
Atunci chiar daca firmele isi doresc maximizarea profitului, de ce nu ajung la o intelegere pentru a stabili nivelul de output qm. Intr-un joc cu o singura mutare, firmele vor coopera doar daca vor obtine din partea concurentei un angajament ferm ca se va pastra nivelul de output stabilit. Astfel, incercarea de a coopera va da gres, deoarece (q1m, q2m) nu e un echilibru Nash.
Pentru acesta sa presupunem ca managerii celor doua firme
se intalnesc (nu neaparat intr-un cadrul formal) si se inteleg asupra unui
nivel de output (q1m, q2m) (sau
orice alt nivel (q1, q2) diferit de (q1c,
q2c)). Cand ajunge fiecare sa firma si isi stabileste
planul de productie, urmatorul gand ce va trece prin minte: daca cealalta firma
produce qjm, ce mai bun raspuns al firmei i nu este qim,
ci ![]() (e evident ca
(e evident ca ![]() ).
Indicele "t" vine de la "trisat": firma i "triseaza", producand mai mult decat
era stabilit, obtinand un profit mai mare. Insa firma i isi da seama ca si
firma j poate urma acelasi rationament si, deci, prin acelasi proces descris
mai devreme se ajunge la echilibrul Cournot-Nash.
).
Indicele "t" vine de la "trisat": firma i "triseaza", producand mai mult decat
era stabilit, obtinand un profit mai mare. Insa firma i isi da seama ca si
firma j poate urma acelasi rationament si, deci, prin acelasi proces descris
mai devreme se ajunge la echilibrul Cournot-Nash.
Cum ar putea totusi firmele sa ajunga la o intelegere, sa
obtina acel angajament ferm? O posibilitate ar fi incheierea unui contract ce
prevede penalitati cel putin ![]() in cazul in care i triseaza. Oricum, in multe
tari astfel de contracte sunt ilegale, deci nu poate obliga partile. Exista
posibilitatea pedepsirii prin sanctiuni de piata (razboi al preturilor). In
jocurile cu o mutare insa nu exista o perioada viitoare in care sa fie puse in
aplicare sanctiunile. Daca nu reusesc o alta cale de a obtine increderea in
celalalt, firmele nu vor putea sa se inteleaga la o pereche de output-uri mai
profitabila decat (q1c, q2c).
in cazul in care i triseaza. Oricum, in multe
tari astfel de contracte sunt ilegale, deci nu poate obliga partile. Exista
posibilitatea pedepsirii prin sanctiuni de piata (razboi al preturilor). In
jocurile cu o mutare insa nu exista o perioada viitoare in care sa fie puse in
aplicare sanctiunile. Daca nu reusesc o alta cale de a obtine increderea in
celalalt, firmele nu vor putea sa se inteleaga la o pereche de output-uri mai
profitabila decat (q1c, q2c).
2.2 Modelul Stackelberg
Ipoteza de la care pleaca acest model este anuntarea de catre firma 1 (leader) a nivelului de output si, odata facut acest anunt, nu se poate reveni asupra lui (spre deosebire de modelul Cournot in care se pleca de la ipoteza anuntarii simultane a nivelului de output). In rationamentul sau, firma 1 are in vedere faptul ca firma 2 va alege cel mai bun raspuns al sau si in raport cu nivelul de output anuntat. Ar fi lipsit de sens din partea firmei 2 sa aleaga nivelul sau de output Cournot, deoarece firma 1 nu isi mai poate schimba output-ul initial. Asadar, firma 1 are posibilitatea de a obtine un angajament credibil asupra unui nivel de output. Atunci, problema este: care e nivelul optim de output al firmei 1?
Pentru orice nivel q1, firma 2 va alege ![]() cel mai bun raspuns. In consecinta, firma 1
alege q1 astfel incat sa-si maximizeze profitul
cel mai bun raspuns. In consecinta, firma 1
alege q1 astfel incat sa-si maximizeze profitul ![]() cu
cu ![]() .
.
![]()
Rezolvam sistemul:
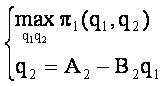 à l
à l
![]()
![]() è
è ![]()
![]() è
è ![]()
![]() è
è ![]()
è ![]()
è ![]()
è ![]()
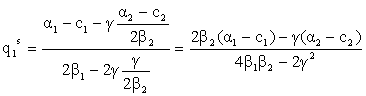
Evident q1s>q1c.
Pentru cazul produselor omogene ![]()
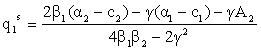 ;
; 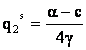
Pentru cazul produselor omogene avem:
![]() q1s = q1m
+ q2m
q1s = q1m
+ q2m
dar ![]() è q1s
+ q2s > q1m + q2m
deci, iarasi profitul total nu este maxim.
è q1s
+ q2s > q1m + q2m
deci, iarasi profitul total nu este maxim.
![]()
![]()
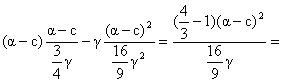
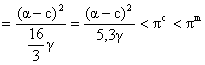
Deci profitul total e chiar mai mic si decat in cazul echilibrului Cournot-Nash.
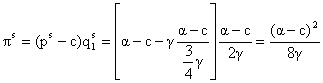
è ![]()
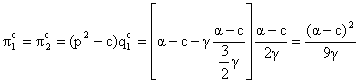
Asadar p s > p c, deci profitul firmei 1 e mai mare in cazul modelului Stackelberg, decat la echilibrul Cournot-Nash, reflectand avantajul primei mutari.

Figura 2 Stabilirea output-ului Stackelberg
- curbele p p s p c reprezinta curbe de izoprofit pentru firma 1 (p >p s>p c
Profitul firmei 1 scade pe masura ce urmam pe figura (daca pastram constant un nivel q1, pentru cantitati din ce in ce mai mari q2, profitul p va scadea). Pantele de maxim ale acestor curbe vor fi, bineinteles, pe curba functiei celui mai bun raspuns al sau. Firma 1 stie ca firma 2 va da cel mai bun raspuns al ei la nivelul sau de output. Deci va cauta sa gaseasca acele puncte de pe curba celui mai bun raspuns al firmei 2 care ii maximizeaza propriul profit. Echilibrul Stackelberg e dat de punctul de tangenta al unei curbe de izoprofit la curba de reactie a firmei 2.
Panta curbei de izoprofit: 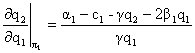
Panta curbei de reactie: ![]()
è ![]()
Echilibrul Stackelberg e de asemenea un echilibru Nash al jocului definit de ipoteza ca firma 1 stabileste un output inaintea firmei 2. Daca firma stie cu siguranta ca firma 1 va alege q1s, atunci va dori in continuare sa aleaga nivelul de output q2s; daca firma 1 stie, de asemenea, cu siguranta, ca firma 2 va alege cel mai bun raspuns la alegerea sa, ea nu va dori sa se angajeze sa produca alt nivel de output decat q1s.
Acum ar putea apare urmatorul contra-argument: daca firma 1
stie ca firma 2 va alege q2s, atunci ![]() (ca cel mai bun raspuns la q2s)
va produce un profit mai mare decat q1s.acest
contra-argument nu are consistenta, pentru ca ne-am afla intr-un alt joc (dat
de alte ipoteze). Daca firma 1 isi poate revizui nivelul de output in functie
de alegerea firmei 2, e contrazisa ipoteza modelului Stackelberg; si apoi cand
firma 1 va anunta
(ca cel mai bun raspuns la q2s)
va produce un profit mai mare decat q1s.acest
contra-argument nu are consistenta, pentru ca ne-am afla intr-un alt joc (dat
de alte ipoteze). Daca firma 1 isi poate revizui nivelul de output in functie
de alegerea firmei 2, e contrazisa ipoteza modelului Stackelberg; si apoi cand
firma 1 va anunta![]() ,
firma 2 va alege cel mai bun raspuns
,
firma 2 va alege cel mai bun raspuns ![]() (vezi figura 2). In acest caz, insa ne aflam
in jocul dat de ipotezele lui Cournot. Firma 1 nu se va angaja niciodata sa
produca
(vezi figura 2). In acest caz, insa ne aflam
in jocul dat de ipotezele lui Cournot. Firma 1 nu se va angaja niciodata sa
produca ![]() pentru ca firma 1 va alege
pentru ca firma 1 va alege ![]() ,
obtinand un profit mai mic decat in caz (q1s; q2s).
,
obtinand un profit mai mic decat in caz (q1s; q2s).
Asadar echilibrul Stackelberg are sens cand firma leader se angajeaza credibil sa produca nivelul de output anuntat.
2.3 Modelul Bertrand
Pana acum s-a propus ca firmele sa stabilesc nivelul de output, preturile fiind determinate prin functia cererii inverse. In multe piete oligopoliste, firmele stabilesc intai preturile si apoi vand cat cere piata. In situatia in monopol, nu conteaza daca analiza se face prin preturi sau prin cantitati (se ajunge la acelasi rezultat). In oligopol insa, alegerea variabilei de analiza e esentiala (J. Bertrand).
Ipoteza modelului: firmele aleg preturile simultan si independent si vand output-urile generate de functia de cerere. Ce sistem de preturi se va alege?
Stabilim curbele de reactie ale celor doua firme in acest caz. Pentru firma i avem de rezolvat urmatorul program de parametru pj:
![]()
![]() vezi relatia
vezi relatia
![]() è
è
![]()
Curbele de reactie sunt drepte cu panta pozitiva. Echilibrul va fi evident (ca si in cazul Cournot) la intersectia celor doua drepte:
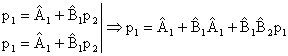
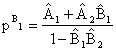 ;
;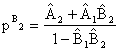
Echilibrul Nash in modelul Bertrand e o pereche de preturi. Rationamentul ce nu asigura ca (p1B, p2B) e un echilibru Nash e asemanator celui de la modelul Cournot. Nici o alta pereche nu are proprietatea de consistenta naturala.
Se demonstreaza ca preturile de echilibru (p1B, p2B) sunt mai mari decat costurile marginale (c1, c2), de unde rezulta ca genereaza profit; pe de alta parte aceste preturi sunt mai mici decat in cazul Cournot, deci nivelele de output sunt mai mari. Asadar sistemul de preturi si de output-uri Bertrand sunt mai competitive decat in cazul Cournot, generand totusi profit.
Sa studiem cazul produselor omogene. Se arata ca pe o astfel de piata p1B=p2B=c, ca in cazul competitiei perfecte. Ca acest cuplu de preturi (p1B=c, p2B=c) e si echilibru Nash se arata urgent. Presupunem ca firma i se asteapta ca firma j sa aleaga pj1>c. cel mai bun raspuns al lui i este pi1= pj1-e e>0. Deoarece, cu acest pret ocupa toata piata, iar pentru e destul de mic obtine cel mai mare profit posibil. Dar i isi da seama ca j gandeste la fel si va plati un pret pj2= pi1-e, asa ca i alege pi2= pj2-e, s.a.m.d. E clar ca, la sfarsit i isi da seama ca j nu poate stabili un pret pj>c. Dar nici o firma nu-si permite sa stabileasca p<c (ar conduce la pierderi). Asadar (p1=c, p2=c) e singura pereche mutual consistenta si deci este echilibru Nash.
Totusi, acest rezultat obtinut pentru o piata cu doua firme si produse omogene, identic cu rezultatul de pe o piata cu competitie perfecta e mai putin plauzibil. Aceasta problema nu apare neaparat ca o imperfectiune a ipotezei lui Bertrand conform careia se aleg preturile ca variabile de decizie. Principala cauza este ipoteza jocului cu o singura mutare.
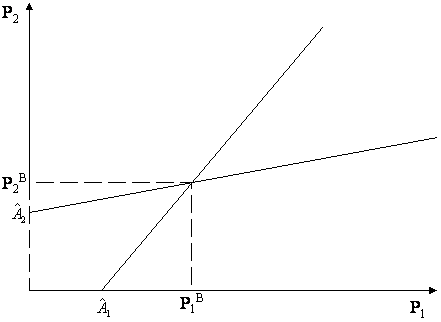
Figura 3 Echilibrul Bertrand
2.4 Modelul Edgeworth
Sa presupunem ca in modelul Bertrand cu bunuri omogene
fiecare firma are data exogen o limita superioara a productiei ![]() (ipoteza
realista, considerand limitarea capacitatilor de productie). Asadar, in
alegerea preturilor, firmele trebuie sa tina cont si de restrictiile
(ipoteza
realista, considerand limitarea capacitatilor de productie). Asadar, in
alegerea preturilor, firmele trebuie sa tina cont si de restrictiile ![]() ,
i=1,2.
,
i=1,2.
Pentru simplificarea analizei presupunem ![]() .
De asemenea, presupunem c1=c2=0. Acesta implica (avand in
vedere ca firmele au o capacitate determinata exogen, deci realizarea unui
output de pana la
.
De asemenea, presupunem c1=c2=0. Acesta implica (avand in
vedere ca firmele au o capacitate determinata exogen, deci realizarea unui
output de pana la ![]() implica doar costuri fixe) faptul ca
maximizarea profitului reprezinta
aceeasi problema cu maximizarea venitului.
implica doar costuri fixe) faptul ca
maximizarea profitului reprezinta
aceeasi problema cu maximizarea venitului.
Resursele sunt omogene, deci cererea este omogena:
![]()
Curbele de reactie sunt date de:
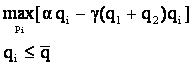
Conditia de gradul I: ![]()
è 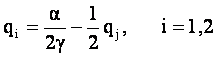
Deci 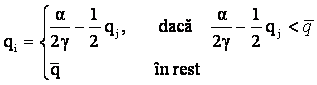
Aceste curbe sunt reprezentate in figura 4
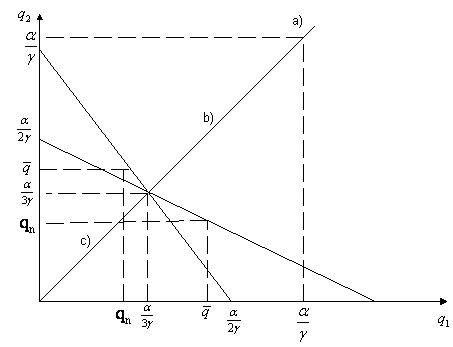
Figura 4 Curbele de reactie ale firmelor
Nivelurile de output Cournot-Nash sunt ![]() (sa nu uitam ca c=0). Acest punct (dat de
ouput-urile Cournot-Nash) se afla pe dreapta la 450, ca si capacitatile
firmelor
(sa nu uitam ca c=0). Acest punct (dat de
ouput-urile Cournot-Nash) se afla pe dreapta la 450, ca si capacitatile
firmelor ![]() .
.
In functie de marimea capacitatii ![]() ,
avem trei tipuri de solutii pentru acest joc:
,
avem trei tipuri de solutii pentru acest joc:
a)
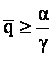 : fiecare firma are capacitatea de a satisface singura intreaga cerere
la pretul egal cu costul marginal p=0;
: fiecare firma are capacitatea de a satisface singura intreaga cerere
la pretul egal cu costul marginal p=0;
b)
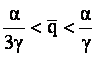 : capacitatea firmei e mai mica decat in cazul a) dar mai mare decat
nivelul de echilibru Cournot-Nash;
: capacitatea firmei e mai mica decat in cazul a) dar mai mare decat
nivelul de echilibru Cournot-Nash;
c)
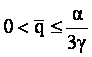 : capacitatea firmei e sub nivelul Cournot-Nash.
: capacitatea firmei e sub nivelul Cournot-Nash.
In cazul a) echilibrul Nash al jocului de stabilire a pretului cu capacitati de productie limitate este de p1=p2=0, care este si solutia Bertrand pentru c=0. Restrictiile de capacitate nu au nici un efect deoarece fiecare firma poate vinde atat cat cere intreaga piata la pretul egal cu costul marginal.
Cazurile interesante, in care apare distinctia fata de modelul Bertrand sunt b) si c). Inainte de a le analiza, sa stabilim doua ipoteze:
distributia egalitara - daca firmele stabilesc acelasi pret atunci fiecare va vinde jumatate din cantitatea ceruta de piata la acelasi pret;
rationalizarea eficienta - daca firma j
stabileste un pret mai mic decat firma i si vinde pana la capacitatea maxima ![]() ,
atunci firma i se va confrunta cu curba cererii reziduale:
,
atunci firma i se va confrunta cu curba cererii reziduale:
![]()
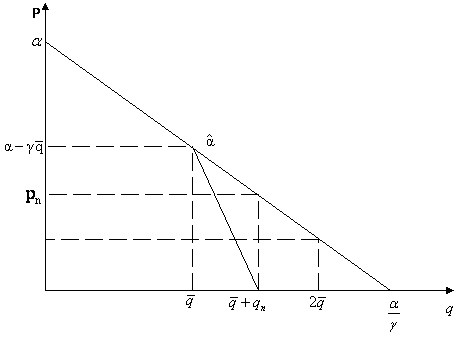
Figura 5 Cererea totala si cererea reziduala
Pretul po la care cererea egaleaza capacitatile
combinate ale celor doua firme este ![]()
Daca 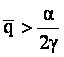 è p0=0.
è p0=0.
Sa aratam ca firmele nu vor alege un pret mai mic decat po.
Daca firma j alege pretul pj>=p0,
firma i va putea vinde ![]() la orice pret pi<=p0;
deci firma 1 va alege pi=p0 caci ii aduce un profit mai
mare decat orice pret pi<p0.
la orice pret pi<=p0;
deci firma 1 va alege pi=p0 caci ii aduce un profit mai
mare decat orice pret pi<p0.
Daca firma j alege pj<p0, ea isi
va vinde intreaga capacitate ![]() ,
insa firma i va putea in continuare sa vanda si ea
,
insa firma i va putea in continuare sa vanda si ea ![]() cu pretul cel putin p0. Deci pi<p0
nu e un raspuns optimal la strategia pj<p0, asa cum nu
e un raspuns optimal la strategiile pj>=p0. In
consecinta, orice pret pi<p0 nu e cel mai bun raspuns
la nici o strategie a firmei j. Deci strategiile pi<p0
sunt strategii dominate de strategia p0.
cu pretul cel putin p0. Deci pi<p0
nu e un raspuns optimal la strategia pj<p0, asa cum nu
e un raspuns optimal la strategiile pj>=p0. In
consecinta, orice pret pi<p0 nu e cel mai bun raspuns
la nici o strategie a firmei j. Deci strategiile pi<p0
sunt strategii dominate de strategia p0.
O alta proprietate importanta a lui p0 e aceea
ca, daca firma j stabileste un pret pj>p0, cea mai
buna strategie nu e de a stabili acelasi pret pi=pj.
Ipoteza distributiei egalitare in cazul pi=pj>p0
implica faptul ca va vinde o cantitate ![]() [2]
la pretul pi. Daca stabileste pretul pi= pj-e, firma i va vinde
[2]
la pretul pi. Daca stabileste pretul pi= pj-e, firma i va vinde ![]() ,
obtinand un profit suplimentar
,
obtinand un profit suplimentar
![]()
(pentru e destul de mic).
Sa consideram cazul b):
Curbele de reactie au alura din figura 6. Daca firma j
alege un pret pjU<peU, cel mai
bun raspuns este pretul pn, pretul corespunzator output-ului ![]() maximizator de profit.
maximizator de profit.
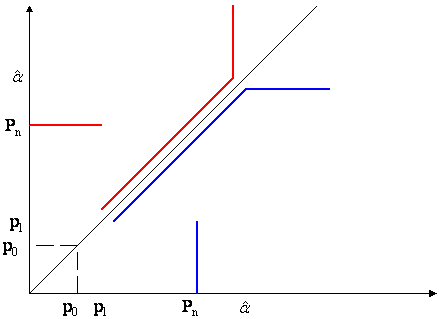
Figura 6 Curbele de reactie ale firmelor 1 si 2
Daca firma j alege un pret pj intre pq
si ![]() ,
firma i va raspunde cu pi= pj-e (s-a vazut mai devreme).
,
firma i va raspunde cu pi= pj-e (s-a vazut mai devreme).
Daca firma j alege un pret ![]() ,
atunci firma i va putea alege pretul maxim la care isi poate vinde intreaga
capacitate
,
atunci firma i va putea alege pretul maxim la care isi poate vinde intreaga
capacitate ![]() .
.
De vreme ce curbele de reactie nu se intersecteaza, nu avem un echilibru Nash in acest caz.
Observatie: O singura firma,
confruntandu-se cu o cerere ![]() isi manifesta venitul (si profitul caci c=0)
alegand
isi manifesta venitul (si profitul caci c=0)
alegand 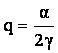 daca e fezabila alegerea sau
daca e fezabila alegerea sau ![]() ,
daca
,
daca 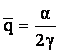 (acest ultim caz corespunde figurii 5).
(acest ultim caz corespunde figurii 5).
Am notat cu pn pretul pe care firma i il
stabileste in conditiile in care firma j are un pret mai mic si vinde la
capacitatea (![]() ).
In aceste conditii firma i se confrunta cu functia de cerere reziduala.
).
In aceste conditii firma i se confrunta cu functia de cerere reziduala.
![]()
Venitul firmei i este ![]() .
.
è venitul marginal 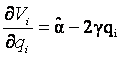 (vezi figura 5).
(vezi figura 5).
Firma i isi maximizeaza venitul è 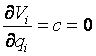 è
è 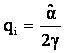 (=qn
notatii)
(=qn
notatii)
è 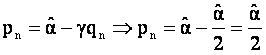
Observatie: In termenii dati de
figura 4, qn e cel mai bun raspuns la stabilirea de catre cealalta
firma a output-ului ![]() .
.
Notam cu pe pretul pentru care firma i e
indiferenta la a vinde intreaga capacitate ![]() fata de a vinde qn cu pn.
fata de a vinde qn cu pn.
![]()
Nu necesita demonstratii faptul ca p0<pe<pn
Datorita discontinuitatii curbelor de reactie in pe, ele nu se vor intersecta si deci nu rezulta nici o pereche de preturi mutual consistente. Edgeworth a vazut aceasta piata ca pe un proces secvential de-a lungul mai multor perioade in care preturile avand o evolutie ciclica la nesfarsit, fara a ajunge la un echilibru. Oriunde ar incepe procesul, preturile vor ajunge sa evolueze in intervalul [pe, pn]. Din pn, in urma unui proces competitiv de coborare succesiva a preturilor, acestea vor ajunge la nivelul pe, de unde vor sari la pn, procesul reluandu-se.
Oricum, noi am considerat jocul intr-o singura mutare. In aceste conditii, nu ne putem pronunta asupra deciziilor pe care le vor lua firmele, neexistand nici un punct de echilibru Nash. Insa nu s-au luat in considerare strategiile mixte. Intr-adevar, nu exista un echilibru Nash de strategii pure in acest joc, asa ca vom determina echilibrul Nash in strategii mixte.
Dar mai intai sa studiem si cazul c).
In acest caz 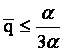
![]() Am vazut ca
Am vazut ca 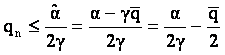
Dar 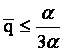
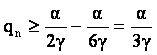
Deci 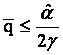 è
è ![]() in
acest caz.
in
acest caz.
![]()
Pe de alta parte: ![]() è
è ![]() è
è ![]()
Deci ![]()
Mai sus (in cazul b) s-a vazut ca preturile cicleaza in intervalul [pe, pn]. Cum in acest caz pe=pn=p0, rezulta ca (p0, p0) e punct de echilibru.
pi= p0 e cel mai bun raspuns al firmei i in cazul in care firma j stabileste un pret la care isi vinde capacitatea; deci pi= p0 e cel mai bun raspuns si in cazul pj= p0. Asadar avem un echilibru Nash in punctul (p1= p0; p2= p0).
Sa revenim la cazul b). Am vazut ca nu exista echilibru Nash in strategii pure. Vom arata ca exista echilibru Nash in strategii mixte, calculand distributiile de probabilitate pe spatiile preturilor ce determina acest echilibru nash.
Prezentam determinarea grafica a punctelor pn si pe (intervalul [pe, pn] se va dovedi singurul in care preturile vor avea probabilitati diferite de 0) (vezi figura). Venitul total al celor doua firme este dat de:
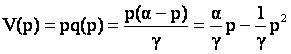
unde 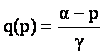 e functia cererii totale (acesta e venitul pe
care l-ar avea un monopolist:
e functia cererii totale (acesta e venitul pe
care l-ar avea un monopolist: 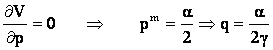 .
Ne reamintim ca aceasta este cantitatea optima a monopolistului:
.
Ne reamintim ca aceasta este cantitatea optima a monopolistului: ![]() cu c=0; aceasta in conditiile in care
cu c=0; aceasta in conditiile in care ![]() adica
adica 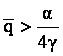 ;
in caz contrar
;
in caz contrar ![]() cand este cantitatea optima a monopolului.)
cand este cantitatea optima a monopolului.)
Notam cu Rn curba venitului firmei care are un pret mai mare si deci se confrunta cu cererea reziduala (firma concurenta a vandut la capacitate).
![]()
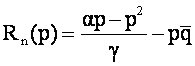
Pn va fi solutia programului ![]() è
è
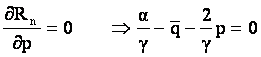 è
è
![]() è
è
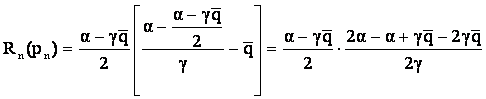
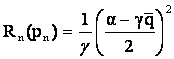 si
si 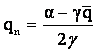
Mai departe avem: ![]()
è ![]() è
è 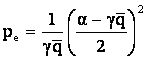
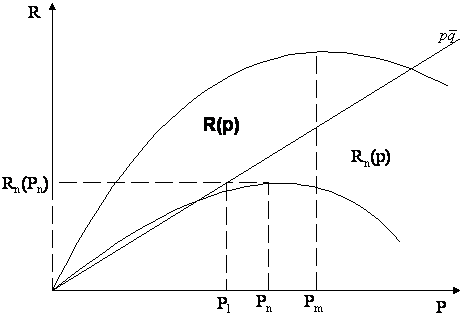
Definim acum strategia mixta pentru firma i: ![]()
![]()
Deci ![]() e probabilitatea ca firma i sa aleaga un pret
mai mic decat p.
e probabilitatea ca firma i sa aleaga un pret
mai mic decat p.
Astfel, daca firma i alege strategia mixta yi, atunci firma j, alegand un pret p, acesta va fi mai mare decat pretul ales de firma i cu probabilitatea yi(p) si mai mic cu probabilitatea 1-yi(p). Venitul asteptat de firma j va fi:
![]()
Asa cum s-a vazut anterior, oricare ar fi preturile de
plecare, acestea ajung sa varieze intre pe si pn. Rezulta
ca nu va fi ales nici un pret din afara intervalului [pe, pn]
è ![]() ,
,
![]() si
si
![]()
A avea un echilibru Nash in strategii mixte in acest joc presupune faptul ca, oricarear fi pretul ales de firma i firma j sa obtina acelasi venit asteptat:
![]()
![]()
![]()
Am folosit faptul ca ![]()
Egalam ![]() è
è
![]()
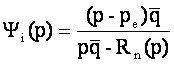
Sa vedem daca yi(p) e o functie de repartitie:
yi(pe)=0 evident
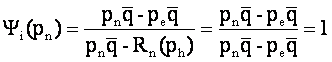
Daca
p>pn, ![]() (a)
(a)
p>pn, ![]() (b)
(b)
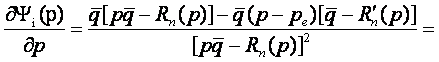
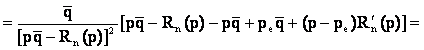
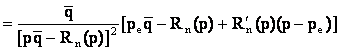
>0 >0 >0
(Pe [pe, ph)
avem ![]() è
è ![]() è
è ![]() )
)
Deci 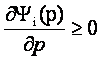
Din (a), (b) si (c) è yi(p) e o functie de repartitie.
Pentru functia de repartitie yi aleasa de firma i, firma j va fi dispusa sa aleaga aleator un pret deci va stabili si ea o functie de repartitie pe sistemul sau de preturi; mai mult decat atat, firma j va alege aceeasi functie de repartitie.
In acest caz, perechea de strategii mixte (y(p), y(p)) reprezinta un echilibru Nash.
2.5 Variabile de decizie: Preturi sau Cantitati?
Modelele de duopol prezentate anterior ne arata importanta variabilei alese. Bertrand crede ca e evident ca firmele sa fie privite ca stabilind pretul, considerand modelul lui Cournot in termeni de cantitati o greseala analitica. O perspectiva moderna care prevaleaza e aceea ca nu trebuie facute astfel de consideratii, fiind o chestiune empirica stabilirea modelului potrivit fiecarei piete in parte. Pe piata analizata, firmele stabilesc productie, permitand apoi preturilor sa se ajusteze pana la curatarea pietei sau stabilesc intai pretul pentru ca apoi sa produca nivelul cerut de piata? Raspunsul la aceasta intrebare va determina modelul ce va fi folosit.
O alta idee din literatura economica ce trebuie urmarita este cea a stabilirii endogene a variabilei. In 1983, Kreps si Scheinkman au extins modelul Edgeworth, in sensul ca permit firmelor sa-si stabileasca endogen capacitatile. Se ajunge astfel la o reconciliere intre modelele Bertrand si Cournot. Astfel, intai firmele isi stabilesc capacitatile de productie si apoi, cu aceste capacitati fixate, se angreneaza intr-un joc de stabilire a preturilor (ca in modelul Edgeworth). Capacitatile de echilibru corespund echilibrului Cournot-Nash. Cu aceste capacitati se trece la stabilirea preturilor si s-a vazut ca nivelul lor egaleaza echilibrul Cournot-Nash. Asadar, avem un echilibru Cournot-Nash intr-un joc in care se stabilesc preturile. Acest rezultat nu e destul de robust in cazul variatiei ipotezelor. In consecinta, problema alegerii variabilei de decizie raman in discutie (vezi Gravelle, Rees - Microeconomics).
Ipoteza de la care se porneste este aceea ca firmele stabilesc preturile sau output-urile in mod repetat, in fiecare dintr-un numar (finit sau infinit) de perioade de timp. Jocul din fiecare perioada va fi numit joc constitutiv, iar firmele participante in acest joc cunosc faptul ca sunt angajate intr-o secventa de repetari a acestui joc. Ele isi vor formula strategii pentru un astfel de joc repetitiv si nu doar pentru un joc constitutiv dintr-o anumita perioada, facand abstractie de perioadele viitoare.
Intr-un fel de context e posibil sa luam in consideratie comportamentul cooperativ, in absenta unor acorduri formale intre firme. Daca firmele accepta (tacit sau explicit) sa coopereze intr-o perioada si daca una din firme se abate de la acord, cealalta firma o poate "pedepsi" trecand la un proces de coborare a preturilor (o crestere a output-ului) sau prin trecerea la alte represalii in perioada urmatoare. Amenintarea unor previzibile represalii viitoare face ca fiecare firma sa nu se abata de la intelegerea facuta. Astfel, firmele se pot intelege in speranta ca acordul va fi sustinut de interesul fiecareia.
Aceasta idee mai trebuie supusa, totusi, analizei. In primul rand, castigul din incalcarea acordului se obtine acum in timp ce pierderile de pe urma actiunii revansatoare a celeilalte firme va fi inregistrata in viitor. Se pune problema daca pierderile viitoare vor fi suficiente pentru a compensa castigurile din abaterea prezenta de la acord. Aceasta depinde de mecanismul prin care actiunile de pedepsire sunt duse la indeplinire de nivelul reducerii castigurilor viitoare, de lungimea perioadei in care firma devianta poate castiga dupa urma comportamentului sau. O a doua chestiune o reprezinta aplicarea unei astfel de politici pe o piata (cum ar fi reducerea preturilor) loveste atat firma care nu a respectat acordul, cat si firma care a aplicat politica respectiva. Amenintarea cu pedepsirea firmei potential deviante isi va avea efectul scontat de intimidare in consecintele in care ar putea fi aplicata efectiv.
O alta problema se reflecta la caracterul finit sau infinit al numarului de perioade in care jocul se va respecta. Sa consideram ca jocul are loc intr-un numar finit de perioade. Atunci firmele au cunostinta despre ultima perioada a jocului. Demonstram prin inductie inversa ca in acest caz cade ipoteza cooperarii intre firme. Echilibrul intr-un astfel de joc va fi dat de jucarea in fiecare perioada a echilibrului Nash a jocului constitutiv.
Demonstratia o vom face pe un exemplu (acesta nu inseamna ca nu e valabila in general). Consideram un joc Bertrand. In ultima perioada nu exista amenintarea strategiilor de pedepsire viitoare si atunci preturile stabilite prin acordul firmelor nu reprezinta un echilibru Nash. Asadar, firmele vor alege echilibrul Bertrand-Nash.
In perioada anterioara firmele ar putea fi de acord sa coopereze, insa acest acord nu poate fi sustinut de strategii credibile de amenintare, deoarece unicul echilibru Nash in subjocul format din ultima perioada e echilibrul Bertrand. Ambele firme sunt constiente de acest lucru si vor actiona in consecinta, alegand pentru penultima perioada echilibrul jocului constitutiv, respectiv echilibrul Bertrand-Nash. Aceasta implica in continuare faptul ca amenintarea cu stabilizarea de preturi non-Bertrand in ultimele doua perioade nu este credibila, deci echilibrul in antepenultima perioada va fi Bertrand-Nash. Rationamentul se extinde perioada cu perioada pana la inceputul jocului. Deci singurul echilibru Nash credibil al jocului respectiv finit este dat de alegerea in fiecare perioada a strategiilor de echilibru Nash pentru fiecare joc constitutiv.
In jocurile repetitive infinite nu exista o ultima perioada unde sa incepem procesul inductiv. Jocul repetitiv va arata la fel, indiferent de momentul de timp in care va fi analizat. In acest caz vom vedea ca o colaborare intre firme e echilibrul Nash al jocului repetitiv.
Sa studiem posibilitatea reala de existenta a unui joc ce se repeta la infinit. Daca astfel de jocuri nu ar exista in realitatea economica, ar fi lipsit de sens sa le analizam (lipsit de sens din punct de vedere economic). Desi oamenii, ca indivizi, au vieti finite, firmele, ca institutii, au vieti potentiale infinite, iar oamenii care le conduc sunt construiti de aceasta. Mai mult decat atat, daca un joc are un numar finit, dar incert de perioade, poate fi analizat ca un joc infinit. Astfel, daca exista posibilitatea p ca va exista o perioada viitoare, atunci va fi si o valoare asteptata a pierderilor de pe urma actiunilor razbunatoare ale firmei inselate. Aceasta valoare asteptata a pierderilor sustine ideea colaborarii intre firme.
1 Posibilitatea cooperarii intre firme
Vom considera cazurile studiate anterior. Orizontul de timp este F=. Se fac alegeri ale output-ului (sau ale preturilor in fiecare perioada t din T). O ipoteza pe care o facem e aceea ca firmele au acelasi factor de actualizare a castigurilor, materializat prin rata dobanzii r>0. Ambele firme au drept criteriu maximizarea profitului:
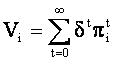
unde 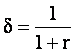 (factorul de actualizare), iar
(factorul de actualizare), iar ![]() e profitul firmei i in perioada t.
e profitul firmei i in perioada t.
Daca presupunem ca firmele coopereaza, alocatia ce maximizeaza profitul total va fi cea care nu intereseaza, pentru ca aceasta confera maxim de castig in acest caz. Oricum, nu trebuie sa ne gandim la acesta ca fiind singura alocatie posibila in cazul cooperarii. Nu e dificil de construit un model in care nivelul de output la Counot Nash conduce una din firme la un profit mai mare decat cel obtinut in urma acceptarii pretului si cantitatii ce maximizeaza profitul total. O astfel de firma nu va fi dispusa sa colaboreze, decat daca platile laterale[3] sunt fezabile.
Daca aceste plati laterale sunt fezabile, firmele isi
maximizeaza castigurile din urma cooperarii, producand q1m+q2m
(sau qm in cazul produselor omogene) obtinandu-se astfel profitul
total maxim pm si apoi
efectuand acele plati laterale (una alteia) care sunt necesare realizarii
acordului. E evident ca profiturile lor ![]() ,
dupa efectuarea platilor laterale, indeplinesc relatiile:
,
dupa efectuarea platilor laterale, indeplinesc relatiile:
![]()
![]() , i=1,2 (sau
, i=1,2 (sau ![]() ,
i=1,2)
,
i=1,2)
Sa presupunem acum ca platile laterale nu sunt fezabile. De exemplu, in multe tari cooperarea de acest gen intre firme e ilegala si deci astfel de plati laterale ar fi o dovada de necontestat a cooperarii lor. O modalitate alternativa de transformare a profiturilor este aceea de a varia output-urile de la nivelurile qim; astfel fiecare firma obtine profit din vanzarea propriului output. Se pun atunci doua intrebari:
Cum vor realiza firmele acest lucru?
Cat le costa acest lucru, in sensul ca, in acest caz, profitul total e mai mic?
In cazul produselor omogene, raspunsurile sunt imediate. Daca firmele mentin nivelul total de output qm, astfel ca pretul sa ramana pm, atunci redistribuirea profitului prin variatia nivelurilor de output e echivalenta in platile laterale. Din moment ce costul e constant si identic c, profitul total nu depinde de modul cum firmele isi aloca intre ele nivelul de output qm.
![]()
![]() è
è ![]()
Aceste consideratii nu mai sunt insa valabile in cazul in care firmele nu au costuri marginale constante sau daca le au constante dar diferite. Astfel, daca costurile marginale nu sunt constante, cresterea output-ului uneia si scaderea output-ului celeilalte duce la scaderea profitului total. Pe de alta parte, daca firmele au costuri marginale diferite dar constante, firma cu cel mai mic cost marginal va produce intregul nivel de output.
In modelul de produse diferentiate, firmele vor incerca sa-si realoce output-urile si profiturile astfel incat, pentru un nivel dat al profitului firmei i, j sa-si maximizeze profitul sau. Formal, acesta se scrie:
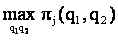
![]() (*)
(*)
Proprietatile functiei pi ne asigura ca solutia acestui model (q1*, q2*) exista si e unica, oricare p . Deoarece (q1*, q2*) e functie de p , atunci si valoarea maximizata a profitului firmei 2, p , e functie de p
![]()
Setul de perechi (p , P(p )) defineste frontiera profitului dand nivelul maxim de profit pentru o firma, cand nivelul de profit pentru cealalta firma depaseste un nivel dat.
Aceasta curba este importanta analiza pe care o vom face in continuare, asa ca vom studia mai in amanunt.
Scriem Lagrangeanul modelului:
![]()
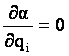 è
è 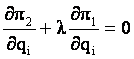 [12]
[12]
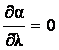 è
è ![]()
In model apare parametrul p . Aplicam teorema plicului.
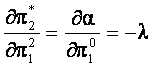
Pe de alta parte, ![]() è
è ![]() (13)
(13)
Din (*) è 
p poate lua
valori in intervalul ![]() ,
unde
,
unde ![]() e acel nivel de profit pentru firma 1, pentru
care valoarea p obtinuta ca solutie a modelului este 0. Se impune aceasta restrictie
deoarece nici o firma nu ar accepta un profit negativ atat timp cat optiunea
nula pentru output si profit este la indemana.
e acel nivel de profit pentru firma 1, pentru
care valoarea p obtinuta ca solutie a modelului este 0. Se impune aceasta restrictie
deoarece nici o firma nu ar accepta un profit negativ atat timp cat optiunea
nula pentru output si profit este la indemana.
Dar 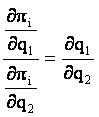 este panta curbei profitului pentru firma i.
este panta curbei profitului pentru firma i.
Asadar frontiera profitului se poate defini ca loc geometric al punctelor in care curbele de izoprofit ale celor doua firme sunt tangente:
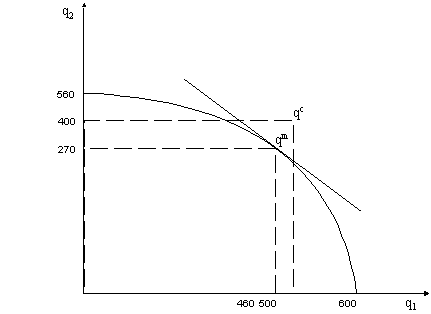
Figura 8 Frontiera profitului in sistemul (q1, q2)
Revenim la relatia (13)
Pentru l=0 se obtine
problema de maximizare a functiei lagrangean: ![]() care e echivalenta cu maximizarea profitului
in conditii de colaborare perfecta (profitul de monopol). Rezulta ca profitul
total maxim se obtine in punctul in care frontiera profitului are panta -1.
care e echivalenta cu maximizarea profitului
in conditii de colaborare perfecta (profitul de monopol). Rezulta ca profitul
total maxim se obtine in punctul in care frontiera profitului are panta -1.
Se duce tangenta 1 de panta -1 (corespunzatoare lui l =1). Punctul de tangenta va fi dat de perechea (p m p m), maximizatoare a profitului total.
Putem raspunde acum intrebarilor puse mai devreme. Daca firmele doresc sa obtina profit, altul decat (p m p m) si daca platile laterale sunt posibile, atunci ele isi pot realoca nivelul de profit miscandu-se de-a lungul dreptei L de ecuatie p pm p .. daca platile laterale nu sunt posibile, atunci realocarea nivelelor de profit prin output le costa pe firme si cel mai rational comportament in acest caz este sa se miste de-a lungul frontierei profitului P(p ). Rezulta astfel un profit total inferior lui pm
Sursa pierderii in profitul agregat este miscarea nivelurilor de output din punctul in care se egalau veniturilor marginale ale celor doua firme (veniturile marginale tineau cont de influenta output-ului unei firme asupra output-ului celeilalte). Avantajul cooperarii consta in internalizarea efectelor externe pe care fiecare firma le exercita asupra celeilalte. Chiar daca aceasta internalizare nu este completa ca in cazul maximizarii profitului total, se observa (vezi figura 2) ca se pot obtine profituri mai ridicat pentru ambele firme decat in cazul echilibrelor necooperative.
Am stabilit asadar stimulente la cooperare, dar aceasta cooperare va fi valabila?
Sa presupunem ca firmele accepta sa produca (q1*, q2*), pereche de output-uri ce le situeaza pe frontiera de eficienta P(p ), undeva pe arcul CC' (figura 3).

Figura 9 Multimea alocatiilor de profit ce pot fi sustinute
de echilibrul Cournot-Nash
O alta ipoteza pe care o facem e aceea ca firmele stabilesc cantitati si nu preturi (joc de tip Cournot).
Pentru sustinerea acordurilor, firmele stabilesc urmatoarele strategii menite sa le impiedice sa se abata de la cooperare:
daca firma i produce qi* in perioada t, atunci firma j va produce qj* in perioada t+1;
daca firma i se abate si produce qiR <>qi* in perioada t, atunci firma j va produce cantitatea sa de echilibru Cournot-Nash qjc in perioada t+1 si in fiecare perioada ce urmeaza.
Astfel, o deviatie a unei firme de la cantitatea stabilita de comun acord implica automat trecerea celeilalte firme la cantitatea de echilibru Cournot-Nash.
Presupunem ca la momentul t=0 firma i se abate de la
acordul de cooperare. Din moment ce se asteapta ca firma j sa produca qj*,
cel mai bun raspuns este ![]() ,
obtinand
,
obtinand ![]() .
Rezulta un castig imediat
.
Rezulta un castig imediat![]() [5].
Conform strategiei piedica, firma i se va confrunta cu qjc
in fiecare perioada t>=1, obtinand un profit pic.
Pierderea viitoare actualizata suferita de firma i va fi:
[5].
Conform strategiei piedica, firma i se va confrunta cu qjc
in fiecare perioada t>=1, obtinand un profit pic.
Pierderea viitoare actualizata suferita de firma i va fi:
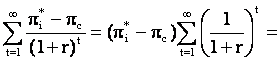
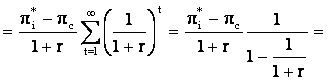
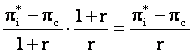
Firma i nu va fi tentata sa devieze in conditiile in care castigul pe care l-ar obtine trisand o data nu compenseaza pierderile pe care le va suferi in viitor.
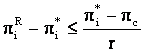
![]()
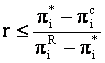
Deoarece un joc repetitiv infinit e identic indiferent de momentul t in care e considerat, daca aceasta ultima conditie e satisfacuta la un moment dat, ea va fi satisfacuta in orice moment. Satisfacerea acestei conditii atrage dupa sine stabilitatea permanenta a output-urilor (q1*, q2*).
Astfel, jocul repetitiv are un echilibru Nash:
daca 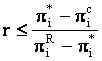 ,
strategiile de amenintare sustin cooperarea si punctul (q1*,
q2*) va fi jucat in fiecare perioada. Daca firma i se
asteapta ca j sa produca qj* atunci va produce qi*
si invers.
,
strategiile de amenintare sustin cooperarea si punctul (q1*,
q2*) va fi jucat in fiecare perioada. Daca firma i se
asteapta ca j sa produca qj* atunci va produce qi*
si invers.
daca 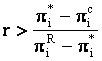 fiecare firma gandeste ca cealalta va fi
tentata sa triseze, si constienta ca acelasi rationament il face si firma
concurenta, va juca direct nivelul de echilibru Cournot-Nash, rezultand echilibrul
Nash dat de (q1c, q2c).
fiecare firma gandeste ca cealalta va fi
tentata sa triseze, si constienta ca acelasi rationament il face si firma
concurenta, va juca direct nivelul de echilibru Cournot-Nash, rezultand echilibrul
Nash dat de (q1c, q2c).
Asadar, strategiile piedica prezentate formeaza un echilibru Nash.
Cooperarea sustinuta de strategiile piedica date de pedepsirea Cournot-Nash e un echilibrului al subjocului perfect, in sensul ca amenintarea cu pedepsirea este credibila. Aceasta presupune ca, in momentul in care firma i observa ca firma j se dezice de angajamentul luat, strategia piedica a firmei i ii spune sa produca qic in fiecare perioada ce urmeaza. Cel mai bun raspuns al firmei j este qjc. Alegerea perechii (q1c, q2c) in fiecare perioada este un echilibru Nash al acestui subjoc. Asadar strategiile piedica satisfac cerintele perfectiunii subjocului.
Nu mai putin adevarat este faptul ca ne putem indoi de rezonabilitatea acestor strategii piedica. Pedepsirea permanenta pare a fi extrem de aspra si are efecte negative asupra ambilor jucatori, in sensul ca nivelul de output Cournot-Nash este mai putin profitabil pentru firma i decat anumite rezultate dintr-o cooperare. Atunci ne putem astepta ca firma j sa propuna firmei i sa "ierte si sa uite" si sa revina la cooperare. Dar, daca la inceput aceste strategii piedica pareau de succes, acum, in momentul renegocierii lor, credibilitatea amenintarii e pusa sub semnul intrebarii.
O alta dificultate cu pedepsirea Cournot-Nash e aceea ca nu poate fi foarte severa daca nivelul de echilibru Cournot-Nash e apropiat de frontiera de eficienta. Acesta inseamna ca exista o multime relativ restransa de puncte pe si sub frontiera de eficienta care sa sustina cooperarea pentru o anumita rata a dobanzii r>0.
Sa analizam in continuare cateva strategii de amenintare care sa extinda posibilitatile cooperarii.
Amenintarile de tip minimax pot sustine orice alocatie cooperativa rationala ca echilibru Nash al unui joc infinit. Acesta cunoscuta ca fiind teorema Folk .
O pedeapsa minimax este cel mai rau lucru pe care o firma il poate face alteia, cunoscut fiind faptul ca firma pedepsita va da totusi cel mai bun raspuns la aceasta strategie. Presupunem ca firma 1 pedepseste firma 2, perechea de output-uri rezultanta (q1*, q2*) fiind solutia programului:
![]()
S-a vazut ca curba de reactie a firmei 2 e data de:
q2=A2-B2q1
Facand aceasta substitutie, ramane de rezolvat:
![]()
Observatie:
q2=A2-B2q1
maximizeaza profitul firmei 2, in conditiile in care q1 este dat;
deci ![]()
Rezolvam acest program:
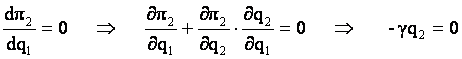
è 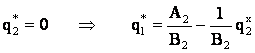 è
è 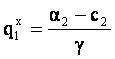
Apar insa mai multe dificultati. Prima este data de faptul
ca aceasta pedepsire poate sa nu fie fezabila. Cu q2=0, cantitatea
maxima pe care firma 1 o poate vinde stabilind pretul p1=0 este 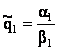 ,
care poate fi mai mica decat q1*. Cand parametrii
modelului conduc la o asemenea situatie, firma 1 va minimaximiza profitul
firmei 2 producand cantitatea maxima vandabila q10 la
pretul p1=0.
,
care poate fi mai mica decat q1*. Cand parametrii
modelului conduc la o asemenea situatie, firma 1 va minimaximiza profitul
firmei 2 producand cantitatea maxima vandabila q10 la
pretul p1=0.
![]()
O a doua problema e aceea ca, firma 1 alegand q10
(la pretul p1=0) se alege cu o pierdere (c1q10).
Aceasta dificultate poate aparea chiar si in cazul in care ![]() ;
in acest caz firma 1 va inregistra profit doar daca p1-c1>0,
deci daca
;
in acest caz firma 1 va inregistra profit doar daca p1-c1>0,
deci daca ![]() .
Insa aceasta conditie nu e in mod necesar satisfacuta. Daca nu e satisfacuta,
pentru a nu inregistra pierderi, firma 1 a putea alege acel nivel de output q1E
pentru care veniturile egaleaza cheltuielile, deci pentru care p1=c1
de unde rezulta:
.
Insa aceasta conditie nu e in mod necesar satisfacuta. Daca nu e satisfacuta,
pentru a nu inregistra pierderi, firma 1 a putea alege acel nivel de output q1E
pentru care veniturile egaleaza cheltuielile, deci pentru care p1=c1
de unde rezulta:
p1-c1=0 è ![]()
Insa pentru acest nivel firma care pedepseste obtine un profit 0, iar firma pedepsita se alege cu un profit pozitiv.
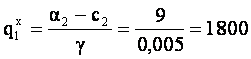
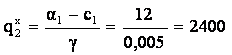
Verificam conditiile de nenegativitate a profitului:
pentru firma 1:
a b q1x-c1=18-0,01*1800-6=-6<0
conditie neasatisfacuta
pentru firma 2:
a b q2x-c2=14-0,008*2400-5=-10*2
conditie nesatisfacuta
Calculam cantitatile maxim vandabile pentru fiecare firma, sub restrictia de a nu inregistra pierderi:
18 - 0,01*q1E- 0,005(562,5 - 0,3125q1E) - 6 = 0 è q1E = 1088,9
14-0,008* q2E - 0,005(600 - 0,25q2E) - 5 = 0 è q2E = 888,9
Daca firma 1 minimaximizeaza firma 2 obtinem:
p
q2=562,5 - 0,3125*1088,9 = 222,21
p2=14 - 1,77 - 5,45 = 6,78 è p mM
Cand firma 1 e minimaximizata, obtinem:
p
q1=600 - 0,25*888,9 = 377,8
p1=18 - 3,77 - 4,45 = 9,78 è p mM
Pana aici, am aratat ca pot exista diferite nivele de output fezabile pentru a pedepsi, depinzand de parametrii modelului.
In continuare vom defini alocatia de profit individual rationala. Fie pix (=0) profitul firmei i cand e minimaximizata prin nivelul de output qjx si piE (>0) profitul ei corespunzator nivelului qjE. O alocatie de profit individual rationala pentru firma i este orice alocatie care conduce la pi>pix in primul caz sau la pi>piE in al doilea caz.
Dupa cum se poate observa in figura, alocarile individual rationale de profit pentru firma 2 sunt reprezentate de punctele multimii delimitate de axe si frontiera de eficienta in primul caz sau de punctele situate intre liniile punctate ce trec prin pE si frontiera profitului.
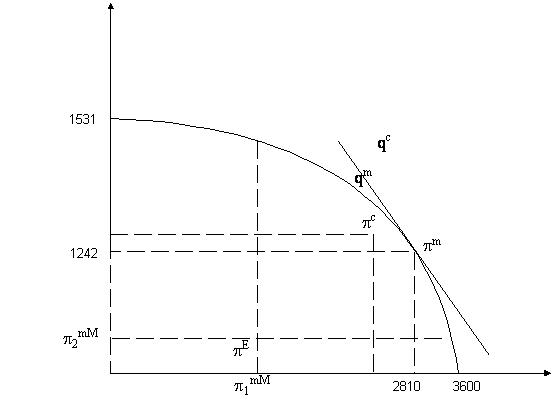
Figura 10 Multimea alocatiilor de profit individual rationale
Teorema Folk stabileste ca strategiile piedica ce includ pedepsirea perpetua prin minimaximizare pot sustine toate alocatiile de profit individual rationale ca echilibru Nash, pentru anumite valori ale ratei dobanzii.
Prin urmare, in comparatie cu pedepsirea Cournot-Nash, strategia minimax extinde considerabil multimea perechilor de output-uri cooperative ce pot fi sustinute cu aceste strategii piedica (sau, cu alte cuvinte, extinde multimea de valori a ratei dobanzii cu care, o anumita pereche de output-uri poate fi sustinuta).
Similar pedepsirii Cournot-Nash, se obtine conditia de credibilitate a strategiilor piedica:
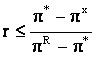 (14)
(14)
Deoarece ![]() ,
avem:
,
avem:
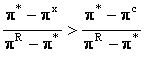
Am aratat astfel ca multimea ratelor dobanzilor e mai mare in cazul folosirii strategiilor minimax pentru sustinerea cooperarii.
Strategiile piedica, constituite pe baza teoremei Folk arata astfel:
Pentru Coca-Cola:
daca European Drinks iese pe piata cu 300 000 de sticle in perioada t, atunci in perioada t+1 va produce 420 000;
daca European Drinks se abate de la nivelul de 300 000 in perioada t, atunci Coca-Cola va produce 1 088 900 de sticle in fiecare perioada incepand cu t+1.
Pentru European Drinks:
daca Coca-Cola vinde 420 000 de sticle in perioada t, atunci va produce 300 000 in perioada t+1;
daca Coca-Cola se abate de la nivelul de 420 000, atunci va produce 889 900 de sticle in fiecare perioada incepand cu perioada t+1.
Aceste strategii determina echilibrul Nash al jocului: daca i crede ca j va juca strategia sa piedica, atunci, in termenii satisfacerii conditiei (12), cel mai bun raspuns al sau va fi propria strategie piedica, rezultand nivelul de output stabilit (q1* q2*) si, implicit, profitul (p p ) jucat in fiecare perioada. Totusi strategiile piedica minimax nu reprezinta un echilibru al subjocului perfect. Sa presupunem ca i triseaza la momentul t si consideram subjocul incepand de la momentul t+1. Firma j minimaximizeaza firma i producand qjx; firma i va raspunde evident cu qix; dar qjx nu e cel mai bun raspuns la qix (singurele output-uri mutual consistente sunt qic si qjc ). Asadar perechea (qix qjx) nu e un echilibru Nash al subjocului considerat.
Asadar, pedepsirea Cournot-Nash poate sa nu fie prea severa, dar cel putin e credibila din punct de vedere al perfectiunii subjocului, in timp ce pedepsirea minimax e destul de severa, dar nu e credibila.
D. Abreu a dezvoltat o idee simpla, dar ingenioasa, care permite pedepsirea mai severa decat prin competitia Cournot-Nash si care ofera strategii perfecte subjocului. Mai mult decat atat, se renunta la pedepsirea perpetua pentru una mai scurta si de scurta durata. Cooperarea e sustinuta de reducerea profitului prin expansiunea output-ului (pentru pedepsirea firmei deviante), pe de o parte, iar pe de alta parte, de revenirea ulterioara la nivelul cooperativ de output; aceasta din urma joaca un rol important in acceptarea pierderii de profit din faza de pedepsire.
Consideram nivelul de output stabilit prin acord de cele doua firme ca fiind (q1*, q2*), cu alocatia de profit (p p ) (alocatie de profit ce poate fi sau nu pe frontiera de eficienta).
Strategiile definite de Abreu sunt urmatoarele:
firmele produc output-ul stabilit in fiecare perioada, atat timp cat in perioada precedenta s-a produs aceeasi cantitate.
daca firma i deviaza in perioada t, atunci firmele vor produce output-uri de pedepsire (pedeapsa vine din partea firmei j) q1P si q2P in perioada t+1.
Observatie:
In general nivelurile q1P si q2P depind de (q1*, q2*)
daca firmele produc cantitatile q1P si q2P in perioada t+1, atunci se va reveni la nivelul (q1*q2*) in perioada t+2.
Observatie:
Devierea in faza de pedepsire va duce la reimpunerea pedepsei, in timp ce acceptarea ei va duce la revenirea la nivelul (q1*q2*).
Notam![]() .
Sa stabilim castigurile si pierderile firmei i in urma devierii de la nivelul
de output stabilit. Castigul imediat este
.
Sa stabilim castigurile si pierderile firmei i in urma devierii de la nivelul
de output stabilit. Castigul imediat este ![]() unde
unde ![]() ,
qiR fiind cel mai bun raspuns la nivelul de output qj*.
In continuare, ambele firme vor produce (qiP, qjP)
astfel ca firma i obtine profitul piP. Daca devierea la momentul t e
profitabila, atunci va fi profitabila si la momentul t+2, ca apoi sa fie
pedepsita la t+3, s.a.m.d. Asadar, sirul profiturilor va fi
,
qiR fiind cel mai bun raspuns la nivelul de output qj*.
In continuare, ambele firme vor produce (qiP, qjP)
astfel ca firma i obtine profitul piP. Daca devierea la momentul t e
profitabila, atunci va fi profitabila si la momentul t+2, ca apoi sa fie
pedepsita la t+3, s.a.m.d. Asadar, sirul profiturilor va fi ![]()
Firma i nu va devia, daca:
![]()
è ![]()
![]()
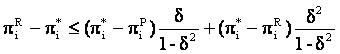
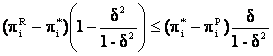
![]()
Dar 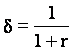 è
è ![]() (15)
(15)
Exista insa niveluri suficient de mari de output care sa genereze profituri piP destul de mici, astfel incat castigul obtinut prin devierea intr-o perioada sa fie mai mic decat pierderea (actualizata) din perioada imediat urmatoare.
Sa schimbam acum ipotezele si sa presupunem ca firma i e
tentata sa triseze si in faza pedepsirii. Consideram subjocul incepand la
momentul t, in conditiile in care firma i a deviat in perioada t-1. La momentul
t, firma i trebuie sa produca qiP si sa obtina profitul piP. Daca
face intr-adevar asa si conditia (15) e satisfacuta, incepand cu momentul t+1
cooperarea va fi stabila, rezultand sirul de profituri pentru firma I ![]() .
.
Valoarea actualizata a acestora la momentul t va fi
![]()
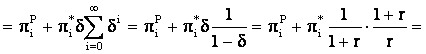
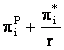
Notam cu qiRP cel mai bun raspuns al
firmei i la qjP rezulta profitul ![]()
qiRP este asadar profitul pe care
firma i il va obtine daca triseaza in faza de pedepsire. Atunci la momentul t+1
se mentin strategiile de pedepsire. Dar, daca firma i considera ca a meritat sa
insele o data in aceasta faza (la momentul t) o va face in continuare, in
fiecare perioada. Sirul de profituri va fi ![]() .
Valoarea actualizata la momentul t a acestor profituri va fi
.
Valoarea actualizata la momentul t a acestor profituri va fi 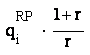 .
.
Pentru ca firma i sa nu se abata de la intelegerea facuta, e necesar ca:
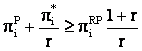
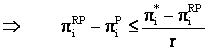
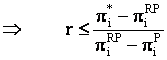
Daca sunt satisfacute simultan conditiile (15) si (16),
atunci alocatia de profit ![]() e sustinuta de strategiile descrise anterior.
De notat ca aceste doua conditii se intaresc reciproc si trebuie indeplinite
simultan. Conditia (15) ne asigura ca firmele nu vor devia, in conditiile in
care, in acest caz, se va recurge la pedepsire; conditia (16) ne asigura ca, nu
jocul de pedepsire va fi intr-adevar instaurat daca se deviaza, in conditiile
in care dupa aceea se va reinstala si mentine cooperare.
e sustinuta de strategiile descrise anterior.
De notat ca aceste doua conditii se intaresc reciproc si trebuie indeplinite
simultan. Conditia (15) ne asigura ca firmele nu vor devia, in conditiile in
care, in acest caz, se va recurge la pedepsire; conditia (16) ne asigura ca, nu
jocul de pedepsire va fi intr-adevar instaurat daca se deviaza, in conditiile
in care dupa aceea se va reinstala si mentine cooperare.
Consideram alocatia de profit (2646; 1380) propusa pentru cooperare. Am vazut ca aceasta corespunde alocatiei de output (420; 300).
In construirea strategiilor piedica urmam urmatorul principiu in faza de pedepsire, firma devianta va produce nivelul de output q* din intelegere, urmand ca firma care pedepseste sa produca cantitatea optima in raport cu nivelul.
Deci:
daca deviaza European Drinks, alocatia de output din faza de pedepsire va fi: (600 - 0,25*300, 300), adica (525; 300), corespunzatoare alocatiei de profit (2756,25; 1192,5) = (p R p P
European Drinks nu va fi tentata sa devieze in prima faza
daca ![]() .
.
Daca deviaza in a doua faza, European Drinks va produce
q2RP=562,5 - 0,3125*525=398,44
p2=8,1875 è p RP
Firma nu va devia daca:
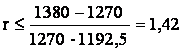
Deci pentru o rata subiectiva a dobanzii mai mica de 69%, European Drinks nu va fi tentata sa devieze.
daca deviaza Coca-Cola, alocatia de output din faza de pedepsire va fi (420; 562,5 -0,3125*420), adica (420; 431,25); alocatia corespunzatoare de profit va fi (2370,5; 1491,26) = (p P p R
Coca-Cola nu va devia, daca:
![]()
Daca deviaza in faza de pedepsire, Coca-Cola va produce:
q1RP=600 - 0,25*431,25 = 492,18
p1=10,922 è p RP
Devierea nu va fi profitabila daca:
![]()
Daca rata subiectiva a dobanzii nu depaseste 128% (corespunzatoare unui factor de actualizare de 19%) firma Coca-Cola nu va dura.
Sa aratam ca aceste strategii sunt strategii de echilibru perfect pentru subjocuri. Sunt patru tipuri de subjocuri:
jocul insusi, inceput la t=0. Daca i se asteapta ca j sa adere la strategiile specificate, in conditiile (15) si (16), cel mai bun raspuns al sau este sa adere la aceste strategii rezultand echilibrul Nash pentru intreg jocul.
un subjoc inceput la momentul t=1, in care nici o firma nu a deviat la momentul t-1. Din moment ce acest joc e identic cu primul, strategiile determina un echilibru Nash pentru astfel de subjocuri.
un subjoc incepand la momentul t=1, in care una din firme (i) a deviat la momentul t-1. Cu conditia (16) satisfacuta, cel mai bun raspuns la qjP e sa produca ea insasi qiP la momentul t, ca la t+1 ambele firme sa produca qi*qj*. Strategiile definite induc un echilibru Nash in astfel de subjocuri.
un subjoc incepand la momentul t=2, in care firma a deviat la momentul t-2, iar la momentul t-1 s-a jucat (q1Pq2P). Acest subjoc e identic cu primul (anterior nu s-a trisat) si deci avem iarasi echilibru Nash.
In concluzie, strategiile definite de Abreu conduc la echilibrul Nash in toate subjocurile posibile, deci sunt strategii de echilibru perfect pentru subjocuri.
Sa notam ca in faza de pedepsire, nu doar firma care pedepseste e inclinata sa suporte costul actiunii sale, dar chiar si firma pedepsita prezinta interes in a coopera la propria pedepsire - ambele firme produc cantitatea de pedepsire qiPqjP. In plus, daca firma i deviaza al momentul t si firma j nu adopta strategia de pedepsire al momentul t+1, atunci din modul de definire al strategiilor, firma i trebuie sa pedepseasca firma j la momentul t+2; cu alte cuvinte, trisorul il pedepseste pe cel inselat pentru ca acesta nu l-a pedepsit pentru inselaciune! Oricum, atat timp cat criteriul folosit pentru credibilitate este perfectiunea subjocului, amenintarile ce deriva din strategii sunt credibile si deci echilibrul Nash va fi dat de jucarea (q1*q2*) in fiecare perioada.
Sustinerea unei alocatii de profit prin strategiile propuse de Abreu depinde de functiile de cost si cerere ale firmelor si de rata dobanzii, din moment ce primele dau profitul firmei, iar ultima ne da valoarea actualizata a castigurilor si pierderilor viitoare. O analiza a abordarii lui Debreu au facut Fredenberg si Maskin (1986), care au aratat ca orice alocatie de profit individual rationala poate fi sustinuta ca echilibru perfect pentru anumite valori ale ratei dobanzii. Ei folosesc pentru faza de pedepsire minimaximizarea reciproca: fiecare firma produce output-ul ce minimaximizeaza profitul celeilalte.
Pierderea[7] suferita de firma devianta va fi mai mare si in general depaseste profitul rezultat din deviere. Consecinta este aceea ca intotdeauna exista o durata a perioadei de pedepsire astfel incat orice alocatie de profit individual rationala sa fie sustinuta de amenintari credibile, bineinteles pentru anumite valori ale ratei dobanzii. Insa pedepsirea prin minimaximizare reciproca e valabila in general doar pentru doua firme. In timp ce toate afirmatiile referitoare la mentinerea cooperarii prezentate anterior se generalizeaza usor la mai multe firme, rezultatele lui Fredenberg si Maskin nu pot fi generalizate.
4.4 Strategii rezistente la renegocieri
Criteriul pe baza caruia am stabilit credibilitatea amenintarilor a fost pana acum perfectiunea subjocului. Ideea care se desprinde din strategiile discutate pana acum este aceea ca firmele se intalnesc, cad de acord asupra unui echilibru cooperativ (q1*q2*), se intelege de asemenea asupra strategiilor (sa spunem de tipul celor prezentate de Abreu) si apoi isi petrec restul timpului implementand aceste strategii, independent una de alta. E ca si cum ar incheia un contract care obliga ambele parti si care nu este renegociabil. Insa, din moment ce acest contract nu leaga partilor in mod legal, ci mai degraba prin propria constrangere, firmele nu pot include si un acord de a nu renegocia strategiile. E imposibil ca partile sa se lege sa nu renegocieze; daca un astfel de acord ar putea fi incheiat si respectat, atunci de ce nu s-ar putea respecta intelegerea initiala cu privire la nivelul de output, fara a mai fi nevoie de strategiile de amenintare?
Sa presupunem ca firma i deviaza la momentul t. Firma j se confrunta acum cu perspectiva pedepsirii firmei i, pentru ca, daca nu o face, conform strategiei Abreu va fi pedepsita de firma i in perioada t+2. Dar daca in acest moment firma i sugereaza firmei j ca, in loc sa aplice strategia de pedepsire (care ii afecteaza pe amandoi), sa renegocieze si sa inceapa din nou? Cu siguranta ca, acest punct, renegocierea unui nou acord ar fi mai buna pentru ambele firme. Insa, daca aceasta renegociere e anticipata ex ante strategiile Abreu nu mai reprezinta un echilibru Nash.
Necesitatea ca strategiile sa fie credibile in sensul ca sunt "rezistente" la renegocieri reduce multimea de alocatii de profit ce pot fi alocatii de echilibru la o submultime de alocatii ce pot fi sustinute ca echilibru perfect al unui subjoc.
Sa presupunem ca firmele stabilesc alocatia de profit (p p ). Daca firma i e pusa in situatia de a pedepsi, trebuie sa fie in interesul sau, mai degraba sa o faca, decat sa permita o renegociere inapoi la alocatia (p p ). Acest lucru este asigurat daca pip>=pip. In plus, alocatia de pedepsire (p p p p) trebuie sa fie ea insasi rezistenta la renegocieri.
Spunem ca alocatia de profit (p p ) e slab rezistenta la renegocieri, daca exista o alocatie de pedepsire (p P p P) slab rezistenta la renegocieri, care:
a) satisface conditiile (15) si (16), astfel ca strategia de pedepsire determina un subjoc perfect;
b) satisface conditia piP>=pi astfel ca firma i nu poate decat sa profite de pe urma pedepsirii, mai mult decat daca ar reveni la echilibru.
Pentru ca pedepsirea firmei j sa aiba intr-adevar efect trebuie sa avem pjP>=pj . Aceasta inseamna ca alocatia (p P p P) nu e dominata in sens Pareto de alocatia (p p ) si invers.
Pentru o credibilitate sporita sunt utilizate strategiile "tare" rezistente la renegocieri. In acest caz, multimea alocatiilor de echilibru la renegocieri se reduce simtitor. O alocatie de profit (p p ) e tare rezistenta la renegocieri, daca e o alocatie slab rezistenta la renegocieri si, in plus, poate fi sustinuta de strategiile de pedepsire, care sunt nedominate Pareto.
Ratiunea rezistentei tari la renegocieri este imediata daca firmele au posibilitatea de a renegocia la orice moment, ele vor prefera o alocatie de output care sa le dea ambelor un profit mai mare; astfel o alocatie dominata Pareto nu e imuna la renegocieri (pentru ca ofera posibilitatea unui profit mai ridicat ambelor firme).
Intr-o situatie de piata de tip oligopol, firmele sunt inclinate spre cooperare pentru ca, in acest mod, pot obtine un profit mai mare decat cel rezultat in urma echilibrului unui joc intr-o mutare de tip necooperativ. Intr-un joc dinamic infinit, se recurge la strategii de amenintare, amenintari care au menirea de a sustine cooperarea. Insa aceste amenintari trebuie sa fie credibile.
Cel mai slab criteriu de credibilitate este perfectionarea subjocurilor. Am vazut ca atat modelul lui Friedman de pedepsire prin competitie Cournot-Nash cat si modelul propus de Abreu satisfac acest criteriu. Putem considera modelul lui Abreu ca fiind mai atractiv pentru firme pentru ca da posibilitatea reluarii cooperarii, dupa aplicarea strategiilor de pedepsire. Pe de alta parte, in cazul competitiei Cournot-Nash, aplicarea strategiilor de pedepsire are repercusiuni si asupra firmei care recurge la ele, lucru valabil uneori si in cazul aplicarii strategiilor lui Abreu. Aceasta parte submina credibilitatea amenintarilor, daca firmele se pot aseza din nou, in orice moment la masa negocierilor.
In consecinta, conditiile de credibilitate sunt intarite prin impunerea conditiilor de rezistenta la renegocieri. Pedepsirea se face prin miscarea spre o alocatie de profit care e mai buna pentru firma ce adopta strategia de pedepsire si mai rea pentru firma pedepsita. In forma sa tare, conditia de rezistenta la renegocieri reduce multimea alocatiilor de echilibrul la o submultime a punctelor de pe frontiera profitului.
Teoriile prezentate furnizeaza ipoteze testabile referitoare la conditiile in care se poate realiza cooperarea; aceste conditii presupun cunoasterea unor parametri referitori la functiile de cost si de cerere ale firmelor, ca si estimarea ratei dobanzii. Ramane totusi o problema in discutie: existenta unui set destul de larg de alocatii de echilibru posibile; teoriile referitoare la credibilitatea strategiilor si modul in care acestea sustin echilibrul unic al pietei. Sunt necesare noi ipoteze care sa permita precizarea unei singure alocatii ca echilibru unic al pietei. Acesta e o chestiune deschisa inca in teoria economica.
In aceasta lucrare, am studiat doar cateva din temele centrale ale teoriei oligopoliste: ipotezele referitoare la alocarea de echilibru pentru produse omogene si diferentiate, in conditiile in care piata e vazuta ca un joc de o singura mutare; conditiile in care firmele pot colabora si sustine aceasta colaborare, intr-o situatie in care firmele interactioneaza repetat pe piata. Restrangerea numarului de firme al doua a avut scopul de a simplifica analiza, generalizarea la mai mult de doua firme fiind directa.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2785
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved