Tomografia computerizata cu rezonanta magnetica nucleara

Tomografia computerizata cu rezonanta magnetica nucleara

Principiul obtinerii imaginilor prin RMN

Folosirea fenomenului de rezonant magnetic nuclear `n aplicatii medicale, pe principiile actuale de obtinere a imaginilor tomografice, se datoreaz biochimistului P.C. Lauterbur si fizicianului J. Mansfield (1973). Rezultatul practic este dezvoltarea tomografiei computerizate, metod de dignostic medical complet neinvaziv, cci nu se bazeaz pe radiatiile aferente radiologiei sau altor metode de investigatie.

Baza fizica a rezonantei magnetice nucleare (RMN) este magnetismul nuclear, caracterizat de momentul unghiular (de spin) si de momentul magnetic, m Gli88 . La actiunea unui camp magnetic extern static B₀ vectorii moment magnetic incearca sa se alinieze directiei acestuia, dupa unghiul q (Figura 8.2). Protonul, care abunda in organismele vii, se afla in doua stari energetice de baza: spin-sus (paralel) si spin-jos (antiparalel), carora le corespund energiile joasa (E₁), respectiv inalta (E₂). Diferenta DE este proportionala cu valoarea lui B₀. Amintim aici c numrul de stri posibile ale nucleelor este de (2I+1), unde I este momentul unghiular intrinsec (sau spinul, ˝ pentru proton).

Prin analogie cu miscarea de precesie a unui titirez in jurul axei verticale de simetrie, sub actiunea cuplului format din campul gravitational si momentul sau cinetic, tot asa protonul executa precesie datorita cuplului creat de momentul magnetic de spin si campul magnetic exterior. Frecventa precesiei depinde de tipul nucleului si de intensitatea lui B₀. La scara macroscopica, numarul suplimentar de nuclee aflate pe nivel energetic scazut (E₁) determina aparitia unei magnetizari longitudinale (M_z), orientata pe directia si sensul campului extern B₀, marime care este folosita pentru inducerea semnalului de RMN in bobina receptorului tomografului.

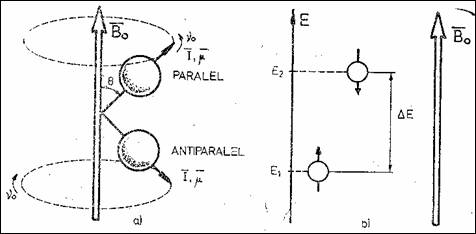
Figura 8.2 Starile nucleelor in camp magnetic

Rezonanta magnetica nucleara. In mod normal, nucleele sunt in echilibru termic, adica numarul de tranzitii din E₁ in E₂ (tranzitii directe) egaleaza numarul tranzitiilor inverse. Acum nu se genereaza semnal detectabil. Producerea tranzitiilor directe poate fi facuta si extern, prin absorbtia radiatiei electromagnetice in impulsuri.

'Rezonanta' intre frecventa campului de RF extern si frecventa precesiei este descrisa de formula

DE = h f₀ ,

unde h este constanta lui Planck iar f₀ este frecventa de precesie nucleara in jurul lui B₀ (frecventa Larmour). Conditia de rezonanta de mai sus se mai scrie

in care g este raportul giromagnetic, o constanta de material. Deci, RMN apare sub actiunea unei energii de RF avand frecventa Larmour, care produce trecerea momentelor magnetice din starea paralela (energie joasa) in cea antiparalela (energie inalta). De exemplu, in cazul protonului (nucleului de hidrogen), pentru B₀ = 1,4 T rezulta f ₀ = 60 MHz. Directia campului de RF `n impulsuri, notat B₁, trebuie sa fie perpendiculara pe directia campului permanent B₀. La egalitatea intre numarul momentelor magnetice pe cele doua stari energetice magnetizarea M_z dispare (Figura 8.3, a), ramanand doar componenta in planul xoy, numita magnetizare transversala (M_xy). Campul B₁, vector ce se roteste sincron cu precesia nucleelor la rezonanta, produce M_xy. Acelasi camp de RF in impulsuri determina rotatia lui M_z in jurul sau (Figura 8.3, b).

Figura 8.4 reda schematic principiul instalatiei de RMN, in care apar impulsul excitator de RF si semnalul-raspuns indus in bobina, numit semnal de inductie nucleara libera (SINL sau FID -Free Induction Decay). Impulsul de RF ce roteste magnetizatia cu 90^o se numeste 'impuls de 90^o' si are ca efect oscilatia lui M_xy cu frecventa f₀. La incetarea excitatiei (B₁) magnetizatia precesioneaza in jurul lui B₀ (precesie liber), M_xy se reduce pana la disparitie iar M_z creste. M_xy induce in bobina-detector o tensiune alternativa de frecventa f₀, a crei amplitudine initial este proportionala cu M_xy, care depinde proportional de densitatea volumica de nuclee excitate. Acesta este semnalul INL (Figura 8.5). Diferentele dintre densitatile protonilor vor fi transformate in imagini RMN.

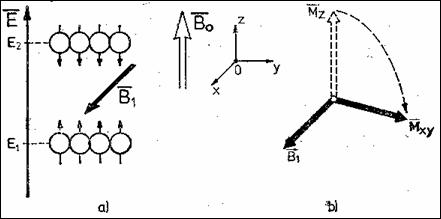
Figura 8.3 Aparitia magnetizarii transversale

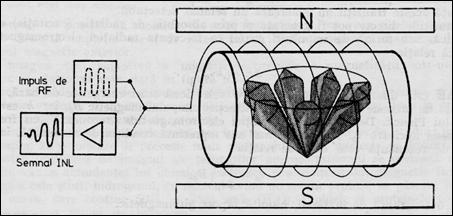
Figura 8.4 Principiul instalatiei de RMN

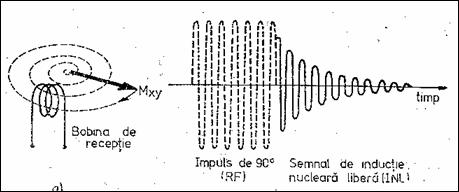
Figura 8.5 Semnalul de inductie nucleara libera (SINL)

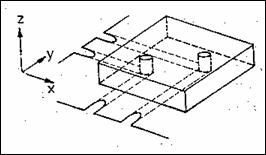
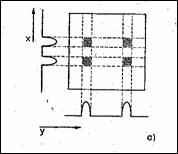
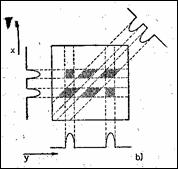
Obtinerea imaginilor RMN In 1973, Lauterbur si Mansfield au pus bazele producerii imaginilor RMN, suprapunand gradientii campului de RF peste campul magnetic static, de-a lungul unei directii. Daca un camp omogen de RF determina o singura frecventa a SINL (Figura 8.6,a), aparitia gradientului conduce la o codificare spatiala a pozitiei probei in planul xoy, caci acum SINL contine un numar de frecvente in spectrul sau egal cu numarul de densitati diferite de protoni, deci de probe elementare (Figura 8.6,b . Folosind transformata Fourier, proba se poate localiza pe directia gradientului (Figura 8.7). Proiectiile celor dou elemente spatiale din Figura 8.8 se obtin similar, succesiv pe x si y. Reproducerea fidela a imaginii probei necesita un numar de proiectii diferite, obtinute prin rotirea gradientului cu cresteri unghiulare mici, precum si folosirea unor tehnici de reconstructie din proiectii (retroproiectie). De exemplu, `n Figura 8.9 se prezint reconstructia fantomei din Figura 8.8 din trei proiectii independente.

 

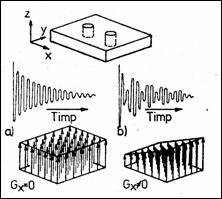
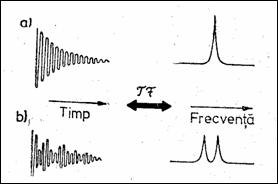
Figura 8.6 Gradienti de camp si SINL Figura 8.7 SINL si transformatele lor Fourier

Figura 8.9 Principiul reconstructiei imaginii din proiectii

Excitarea selectiv a unei sectiuni. Deoarece `n corpul uman densitatea protonilor variaz dup toate cele trei axe, devine necesar excitarea unei sectiuni plane. Excitarea selectiva a unei sectiuni foarte subtiri de-a lungul axei z , de grosime Dz (Figura 8.10), se face aplicand un gradient G_z si alegand o banda de frecventa corespunzatoare pentru impulsul de RF. Astfel, gradientul si ltimea benzii de frecvent limiteaz excitatia doar la sectiunea dorit.

 

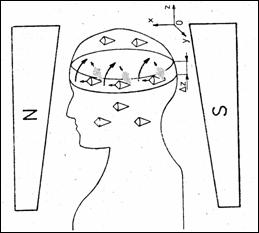
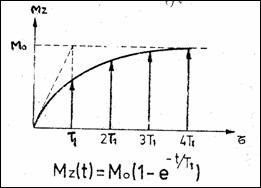
Figura 8.10 Excitarea selectiv Figura 8.11 Variatia magnetizrii M_z

 

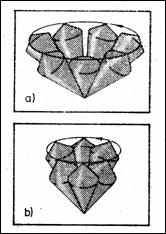
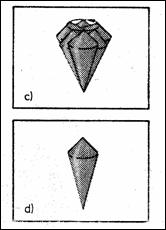
Figura 8.12 Relaxarea spin-mediu

Timpii de relaxare Dependenta magnetizarii transversale nu doar de densitatea protonilor, ci si de caracteristicile intrinseci de miscare, diferentiaza tomografia prin RMN de cea cu raze X. Relaxarea este revenirea magnetizarii la starea de repaus, in directia lui B₀, dupa incetarea impulsului de RF (Figura 8.12).

Deoarece spinii excitati disipa excesul de energie in mediu, timpul de relaxare T₁ se mai numeste timp 'spin-mediu' sau timp de relaxare longitudinala. Procesul este guvernat de relatia exponentiala (Figura 8.11)

.

Timpul T₁ variaza in functie de tesut. Practic, din considerente de raport semnal/zgomot se detecteaza mai multe SINL pentru aceeasi proba. Daca un nou impuls excitator apare mult mai repede decat T₁ al unui anumit tesut, amplitudinea SINL va fi puternic micsorata. Rezulta de aici posibilitatea reglarii contrastului imaginii pentru probe cu densitati de protoni apropiate (de exemplu creier si lichidul cerebrospinal - LCS), numai variind intarzierea t dintre impulsurile de RF. ~n Figura 8.13 este redat variatia ampliudinii SINL functie de t si se remarc un contrast mai bun `n cazul (b), unde LCS (avand T<sub>1</sub> mare) apare mai `nchis.

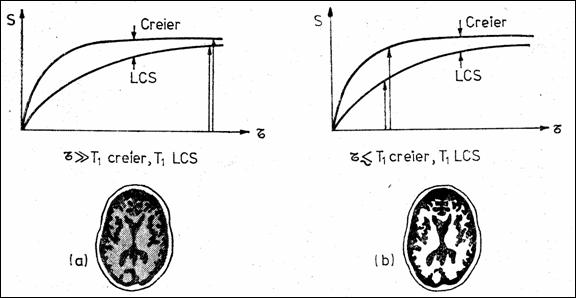
Figura 8.13 Efectul timpilor de repetitie a impulsurilor de RF

Timpul de relaxare T ('spin-spin' sau timp de relaxare transversala) reprezinta constanta de timp care caracterizeaza atenuarea magnetizarii transversale dupa incetarea impulsului de RF:

.

Datorita neomogenitatii magnetilor statici, constanta de timp ce ilustreaza atenuarea SINL este practic mai mica decat T₂. Din acelasi motiv poate aparea o defazare treptata intre vectorii magnetizarii, ceea ce poate produce o atenuare drastica a acesteia. La fluide T₁ T₂ iar la solide T₁ > T₂. Magnetizatiile diferitelor elemente au viteze diferite de precesie, `n functie de valoarea local a campului magnetic static. Apare astfel o defazare treptat a magnetizatiei, care se desfsoar `n evantai (Figura 8.14).

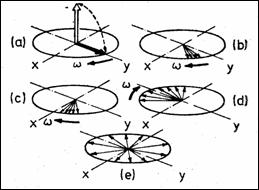
Figura 8.14 Defazarea progresiv a magnetizatiei transversale `n urma impulsului la 90^o

Fenomenul de spin-ecou. Atenuarea magnetizarii transversale datorita lui T₂ este compensata prin aplicarea unui impuls de RF defazat cu 180^o, la t secunde dupa impulsul de 90^o (Figura 8.15,b). Astfel spinii mai rapizi se aliniaza cu cei mai lenti iar la t = 2t are loc refocalizarea completa (Figura 8.15,a). Dac SINL scade cu o constant de timp <T₂, atenuarea spin-ecoului are loc cu T₂ real, constanta de timp spin-spin. Rezulta ca SINL are acum amplitudinea dependenta de raportul t/T₂, de care depind practic stralucirea si contrastul imaginilor tomografice. De exemplu, `n Figura 8.16, a, dac perioada impulsurilor de 90<sup>0</sup> satisface relatia T>>T<sub>1</sub>, imaginea are un anumit contrast. Dac T T<sub>1</sub>, contrastul rezultat depinde de T<sub>1</sub> si de T<sub>2</sub>: pentru `ntarzieri mici (t t_a) creierul apare cu un contrast bun (el are T₂ mic); pentru t t_b contrastul este foarte mic iar dac t t_c semnificatia strlucirilor celor dou tesuturi este invers.

RMN in medicina Nucleul hidrogenului, protonul, este cel mai abundent element din organismele vii. Imaginile RMN indica repartizarea protonilor in sectiune, precum si informatii asupra timpilor de relaxare specifici fiecarui tesut, structurii lor chimice si vitezei de curgere a fluidelor in corpul uman. Alti izotopi cu spin nuclear (¹³C, ¹⁷O,³¹P,¹⁵N) au densitati scazute in tesuturile umane si pot fi greu detectati prin RMN. RMN se aplica in investigarea practic a oricarui tesut si organ uman, dar rezultatele cele mai spectaculoase se inregistreaza in cazul creierului.

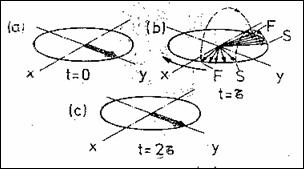
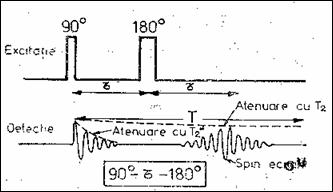
(a) Formarea unui spin-ecou (b) Secventa spin-ecou

Figura 8.15

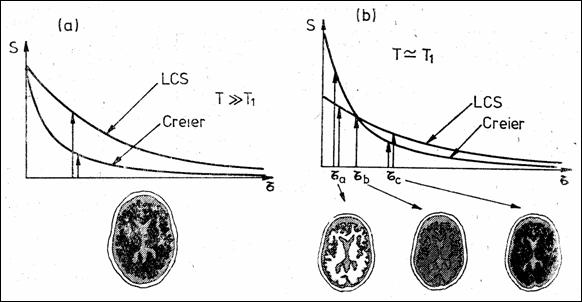
Figura 8.16 Efectul timpului T₂ asupra contrastului imaginilor

Schema bloc a unui tomograf cu RMN

Constructia practica a unui tomograf cu RMN, deosebit de complexa, depinde de modul de excitatie, sistemul de magneti si metodele de reconstructie a imaginilor. O schema bloc principiala este prezentata in Figura 8.17 Gli88

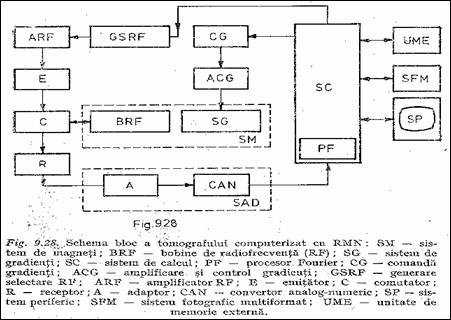
Figura 8.17 Schema bloc a unui tomograf cu RMN

O caracteristica tehnica importanta este absenta pieselor mecanice in miscare, localizarea spatiala a probei facandu-se transformand domeniul frecventa in coordonate spatiale. Sursa de excitatie este un emitator de RF ce produce un camp perpendicular pe campul magnetic static. SINL este obtinut prin inductie in bobina receptorului. Memorarea si reconstructia imaginii se face cu ajutorul sistemului de calcul, in care se remarca procesoarele Fourier dedicate.

Sistemul de magneti este componenta cheie, critica si cea mai scumpa a tomografului. De exemplu, pentru o proba de 0,5 m diametru omogenitatea spatiala si temporala a campului trebuie sa fie de 10100 ppm. Inductiile magnetice folosite, B₀, sunt de 0,152 T (optim in jurul 0,35 T). Cresterea inductiei, desi mareste sensibilitatea, are ca efecte nedorite scaderea raportului semnal/zgomot si a frecventelor inalte in SINL, precum si cresterea pierderilor prin curenti turbionari. Magnetii statici folositi pot fi de tip permanent (din miez feromagnetic premagnetizat, B_0max=0,3T), rezistiv (miez feromagnetic sau conductor din cupru/aluminiu excitat electric, B_0max=0,2T) sau supraconductor (conductor de niobiu-titan la temperatura criogenica, B_0max=2T, foarte scumpi).

Sistemul de gradienti permite rezonanta selectiva a probei si este format din trei bobine de curent continuu ortogonale care produc gradientii liniari G_x,y,z. Spectrul Fourier al SINL (f_i ) reprezinta codificarea in frecventa a coordonatelor spatiale ale punctelor sectiunii. Amplitudinile frecventelor depind de densitatea de protoni si de timpii de relaxare. Sistemul de calcul permite ca gradientii sa fie sincronizati cu baleiajul imaginii. Marimea gradientului determina rezolutia imaginii. Intrucat in corp exista gradienti de fond, datorati neomogenitatilor campului magnetic, valoarea globala a gradientului aplicat trebuie sa fie mare si greu obtenabila, de pana la 10 T/m. Practic se foloseste o secventa de impulsuri de RF si de gradient ca in Figura 8.18. Receptionarea SINL (ecoului) se face la momentul t=10t, cu t ms. Cu succesiunea de gradienti pozitivi si negativi din figura valoarea globala a gradientului aplicat scade de cca. 10 ori fata de metoda directa, la aceeasi rezolutie.

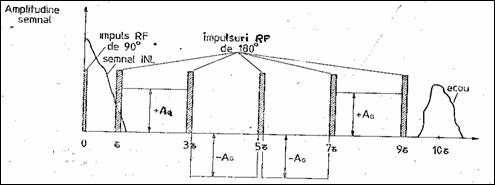
Figura 8.18 Succesiunea impulsurilor de RF si de gradient

Bobina de RF genereaza campul excitator puternic si omogen (B₁), perpendicular pe campul static principal B₀ si culege SINL, avand amplitudini mici.

Emitatorul produce impulsuri de RF foarte stabile, de 1 10 kW, care ajung la pacient mult atenuate (wati). Uzual, campul B₁ este de cca. 5 mT/cca.1 ms (impulsul la 90^o).

Receptorul culege din bobinele de RF SINL, avand amplitudini de ordinul mV, il amplifica si il mixeaza in banda de audiofrecventa.

Sistemul de achizitie de date preia semnalul de la receptor, il amplifica, filtreaza si mixeaza cu semnalul unui oscilator local, il mediaza in adaptor pentru reducerea zgomotului, il converteste in semnal digital, il memoreaza si-l prezinta procesorului Fourier. Sistemul de calcul reconstituie imaginea din proiectii, supervizeaza functionarea celorlaltor blocuri si realizeaza dialogul cu operatorul.

Metode de detectie

Detectia simpla consta in achizitia si prelucrarea SINL imediat dupa aplicarea impulsului de RF. Foloseste pentru imagini doar componenta defazata cu 90^o fata de impulsul de RF a spectrului Fourier. Metoda nu poate fi folosita pentru codificarea spatiala a protonilor.

Detectia selectiva, prezentata deja, ofera respectiva codificare. Pentru un gradient liniar transformata Fourier este proiectia distributiei protonilor excitati de-a lungul gradientului, pe directia perpendiculara pe directia gradientului.

Detectia intarziata (pregatita) a SINL dupa aplicarea excitatiei permite spinilor sa aiba precesie la frecvente dependente de timp si spatiu, in functie de valoarea campului. La sfarsitul acestui timp pregatitor spinii diferitelor zone ale probei s-au rotit cu un unghi proportional cu integrala de timp a campului magnetic. Rezulta astfel o codificare suplimentara a unei coordonate spatiale, de-a lungul gradientului, in fazele SINL ce se detecteaza.

Gradientii oscilanti apar daca bobina de gradient pe o coordonata este strabatuta de curent alternativ. Exista un plan in care gradientul este nul si in care campul rezultant este constant. Pentru o secventa repetitiva de impulsuri de RF, SINL vor fi stabile doar in 'planul nul'. In rest ele au caracter aleator, cu medie zero. Deplasand planul nul de-a lungul axei x si modificand alimentarea bobinei de gradient, se obtine rezolutia unidimensionala. Generalizand metoda pentru celelalte axe se obtin rezolutiile bi- si tridimensionale.

Metode de reconstructie a imaginii

Reconstructia din proiectii

Dupa cum s-a aratat, transformatele Fourier ale SINL reprezinta proiectii fie ale densitatii protonilor, fie valori ale timpilor de relaxare, fie combinatii ale acestor marimi. Pentru cazul bidimensional (2D) problema reconstructiei se formuleaza in cele ce urmeaza.

Fie f (x, y) o functie reala, f : R² R si fie uov un sistem ortogonal rotit fata de sistemul xoy cu unghiul q variabil. Proiectia dupa unghiul q a lui f este data de formula

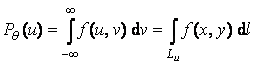
unde L_u este o dreapta paralela cu axa ov (formeaza unghiul q cu axa oy). Problema reconstructiei este de a afla valorile lui f(x, y) stiind proiectiile P_q(u). Pentru cazul discret se afla valorile lui f intr-un numar finit de puncte, cunoscand valorile lui P pentru diferiti q si u. In general, trebuie rezolvat un sistem de ecuatii integrale, lucru aproximat prin metode numerice adecvate. In cazul tridimensional functia f se poate obtine fie dintr-un set de proiectii 2D, paralele cu planul xoy si apropiate intre ele sau din sectiuni plane rotite in jurul unei axe (oy), avand deci simetrie radiala cilindrica. Metodele de reconstructie directa 3D pot folosi atat proiectii 2D cat si multimi de proiectii 1D.

 

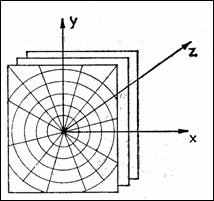
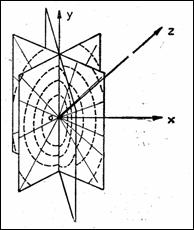
Figura 8.19 Reconstructia 3D

1. Principiul transformatei Radon

Fie f (x,y,z) = f (r) o functie reala 3D, f : R³ R (in particular o functie-imagine). Fie un vector oarecare unitar w si sIR. Transformata Radon a functiei f, R(f ) se defineste astfel incat

unde integrala se ia peste planul definit de ecuatia rw s iar d este functia delta a lui Dirac. Se observa respectarea definitiei proiectiei unei functii. Inversa transformatei furnizeaza valorile functiei initiale:

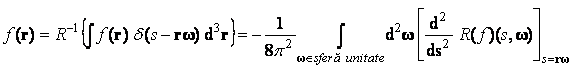
Volumul de calcul fiind foarte mare, transformata Radon are mai mult importanta teoretica.

2. Metoda convolutiei

Pornind de la transformata Radon, functia imagine se exprima ca integrala de convolutie dintre proiectii si o functie filtru. In cazul discret, pretabil calculului numeric, se obtine formula

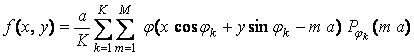
in care

j este functia filtru,

P_jk este proiectia functiei imagine f dupa unghiul j_k

a este pasul de esantionare a proiectiei,

M este numarul de esantioane ale unei proiectii si

K este numarul de proiectii.

Efortul de calcul necesar este relativ redus, insa alegerea functiei filtru este delicata, criteriile de alegere fiind adesea contradictorii. In principiu trebuie folosit un filtru trece-jos cu rol de a minimiza efectul esantionarii asupra proiectiilor. Astfel de filtre sunt filtrul Ram-Lak si filtrul Shepp-Logan. Primul ofera rezolutie buna, contraste mari dar este sensibil la zgomot. O alta varianta de filtre se bazeaza pe metode de cuadratura (Simpson, metoda trapezului etc.), ce calculeaza aproximativ integralele din formula convolutiei. De exemplu, filtrul Horn reduce zgomotul dar si contrastul si taie frecventele inalte. Practic se pot folosi combinatii de filtre diferite, ajungandu-se la compromisuri calitative acceptabile.

3. Metoda transformatei Fourier (TF )

Cheia metodei este ca TF a unei proiectii (n-1)-dimensionale a unei functii n-dimensionale este egala cu sectiunea centrala a TF a functiei. Rotind proiectiile, deci sectiunea TF, se poate reface TF completa si apoi, prin TF inversa, se poate reconstitui functia original. Exemplificam metoda pentru cazul 2D, trecerea la n dimensiuni fiind directa.

Fie f (x, y) functia imagine. TF a ei este

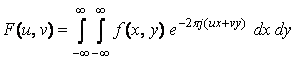
Proiectia lui f pe axa ox se obtine cu formula

.

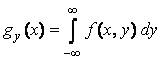TF a proiectiei,

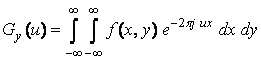
este egala cu sectiunea centrala a TF 2D a lui f:

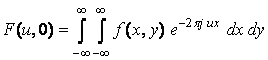
adica

G_y (u) = F(u, 0).

TF a proiectiei lui f pe o axa rotita cu un unghi q este egala cu sectiunea dupa q a TF a imaginii. TF discrete ale proiectiilor produc retele polare de puncte. Pentru obtinerea imaginii in coordonate carteziene este necesara o interpolare 2D in planul Fourier prin care se calculeaza valorile TF in nodurile retelei carteziene.

Algoritmul TF rapide si procesoarele specializate reduc considerabil timpul de calcul, chiar pentru rezolutii spatiale de sute de puncte.

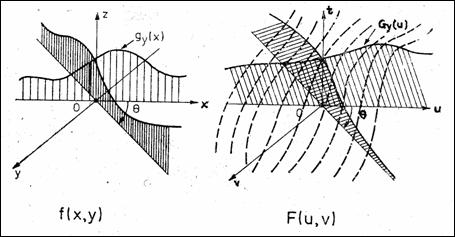
Figura 8.20 Reconstructia transformatei Fourier a imaginii

4. Metode algebrice

Fie f (x, y) o functie imagine de banda limitata,

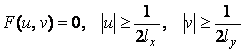
si o retea rectangulara de (I x J) pixeli, definita de punctele (ml_x, nl_y), cu m, n I Z. Proiectia lui f pe o axa oarecare este data de formula

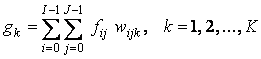
unde w_ijk sunt ponderi ce indica daca dreapta de proiectie intersecteaza elementul (i, j ). Rezulta un sistem de ecuatii cu necunoscutele f_ij, valoarea lui f in punctul (i, j). Sistemul de K ecuatii cu I xJ necunoscute de mai sus este, in general nedeterminat, caci mare parte din w_ij sunt nuli. In plus, s-ar opera cu matrice de mari dimensiuni, lucru total neeconomic. Din aceste motive s-au elaborat metode iterative care determina solutii aproximative ale sistemului de mai sus. Una din metode pleaca de la valori initiale f _ij si determina valori analoage,, la iteratia q:

unde L_k este lungimea razei de proiectie k, N_k este numarul de celule intersectate de raza k iar M_ij este numarul de raze ce intersecteaza pixelul (i, j ). Conditia de oprire este ca marimea

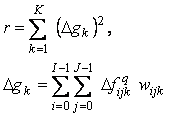
sa fie de acelasi ordin de marime cu energia zgomotului aleator.

5. Reconstructia obiectelor in miscare pe baza paradigmei conexioniste

Metodele de reconstructie prezentate sunt eficiente pentru probe fixe, statice. In cazul unor organe in miscare (inima, plaman) multimea proiectiilor nu este consistenta in raport cu distributia absorbantei probei (proiectiile nu apartin aceleiasi faze a variatiei in timp) si imaginea obtinuta va avea artefacte de miscare. Reducerea timpului de scanare si folosirea unor metode speciale de esantionare nu rezolva complet problema. Folosirea retelelor neuronale artificiale (RN ) pentru reconstructia dintr-o secventa de proiectii esantionate liniar in timp se dovedeste foarte eficienta Chi94 . Formularea problemei este urmatoarea:

Avand o functie de doua variabile s(x,y), transformata Radon a lui s este

,

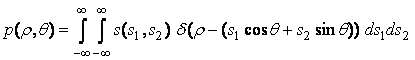in care r I R_m, q I s0, pt si d ) este functia delta a lui Dirac. Secventa de proiectii a obiectului variabil poate fi calculata pentru o multime finita de raze de proiectii, adica

,

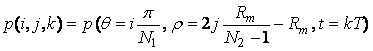pentru i = 0, 1, ., N₁-1, j = 0, 1, ., N₂-1, k = 0, 1, ., N₃-1, T fiind intervalul dintre doua proiectii consecutive. Definind x_k I proiectia completa la momentul kT, incat elementul (i,j) al lui x_k este p(i,j,k), multimea proiectiilor poate fi scrisa ca

I .

Transformata Fourier se scrie sub forma matriceala complexa ca

.

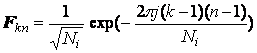Obtinem un sistem de ecuatii liniare avand ca necunoscute proiectiile obiectului variabil in timp. Ecuatiile sistemului se determina astfel:

Infasuratoarea spectrala a proiectiilor trebuie sa aiba forma de arc. Definim U I si u I , incat U = 1_N3x1 A u (A denota produsul Kronecker) iar u(i,j) = 1 in afara spectrului si nul in interiorul sau. Rezulta expresia

, (1)

in care ( ) este produsul matriceal Schur - Hadamard si I_i este matricea identica de dimensiune N_i N_i.

Spectrul temporal al proiectiilor trebuie sa fie de banda limitata. Se definesc W I si w_ij I , incat , pentru i = k modN +3, j = 0, 1, ., N₂-1, k = 0, 1, ., N₁ x N₃ -1 si w_ij = s1.1 0.0 1.1t^T. Numarul de 0 in w_ij(i,j) determina latimea benzii variatiilor temporale ale obiectului. Avem deci

. (2)

Valorile proiectiilor reconstruite, pentru unghiul masurat, trebuie sa fie aceleasi cu valorile proiectiilor masurate, adica X trebuie sa se apropie de datele disponibile, D:

, (3)

unde V I , V(l,m) = 0 daca X(l,m) nu este disponibil si V(l,m) = 1 daca X(l,m) este disponibil, l = 0, 1, ., N₁xN₃ -1 si m = 0,1, ., N₂ - 1.

Ecuatiile (1), (2), (3) formeaza un sistem de ecuatii liniare supradeterminat (necunoscute mai putine decat ecuatii). In locul calcularii exacte a lui X putem folosi modelul conexionist pentru a minimiza eroarea patratica medie totala (MSE) pentru sistemul de mai sus. Rezolvam deci

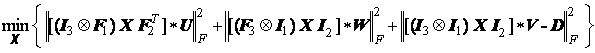.(4)

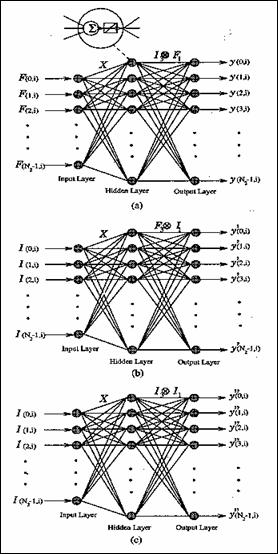
Figura 8.20a Topologia retelei neuronale pentru reconstructie TC

RN a carei antrenare supervizata implementeaza problema (4) este formata din trei subretele, ca in Figura 8.20a. Vectorii de intrare sF(0,i ), F(1,i ), ., F(N₂-1,i )t^T si sI(0,i ), I(1,i ), ., I(N₂-1,i )t^T sunt respectiv coloanele i ale lui si I₂. Vectorul Y de la iesirea RN este

.

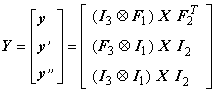Prin antrenare se vor determina valorile ponderilor X (celelalte ponderi sunt fixe), astfel incat iesirea sa aproximeze valorile dorite, conform criteriului de minimizare

.

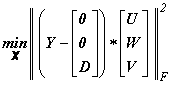Cele trei subretele pot fi antrenate in paralel in timpul fiecarui ciclu de instruire iar la o iteratie se prezinta RN cate o coloana a vectorilor indicati. Rezultatele raportate indica o eroare de reconstructie foarte buna, de cca. 2%.