| CATEGORII DOCUMENTE |
| Aeronautica | Comunicatii | Electronica electricitate | Merceologie | Tehnica mecanica |
Infasurare monofazata care determina p perechi de poli magnetici
Cea mai simpla infasurare monofazata care determina p perechi de poli se obtine prin inserierea a p bobine.
Cazul
unei infasurari cu p=2
este prezentat in figura 2.1.b,
respectiv in figura 2.11.a, unde
reprezentarea s-a facut prin desfasurarea armaturii care
poarta bobinele. Daca fiecare bobina are 
spire, atunci
infasurarea are 
spire:
Fig. 2.11. Infasurare care determina p=2 perechi de poli
a) schema desfasurata; b) tensiunea magnetica din intrefier
Pentru a se asigura
repetabilitatea structurii campului magnetic, cele p bobine trebuie sa fie
identice constructiv si sa fie asezate echidistant la periferia
armaturii, ceea ce presupune ca laturile de bobina prin care curentul
i are acelasi sens trebuie asezate la distanta a doi pasi
polari 
- vezi figura 2.11.a).
Tensiunea magnetica produsa in intrefier are o variatie alternativa dreptunghiulara (vezi figura 2.11.b), determinata prin acelasi procedeu ca in cazul infasurarii monofazate care determina o pereche de poli magnetici (capitolul 2.2.1.1).
Considerand
axa spatiala de referinta suprapusa peste axa de
simetrie a unui pol nord, care corespunde cu axa magnetica a
infasurarii (vezi figura 2.11), rezulta ca tensiunea magnetica este o
functie para, alternativ periodica, cu perioada 
.
Dezvoltand tensiunea magnetica din intrefier in serie armonica se obtine:
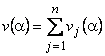
(2.18)
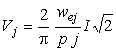(2.18.a)
unde s-a presupus ca infasurarea este parcursa de un curent alternativ sinusoidal de expresie (2.6):
iar numarul de spire echivalent 
pentru armonica j care are expresia:
(2.18.b)
fiind numarul de
spire al infasurarii, iar 
factorul de
infasurare definit de relatia (2.16.c).
Observatie:
In cazul in care bobinele, care
determina perechi diferite de poli magnetici, nu sunt identice, tensiunea
magnetica rezultanta va avea perioada 
si este necesar
sa se considere ca fiecare bobina determina in intrefier o
tensiune magnetica alternativa avand doi poli magnetici; armonica
spatiala de ordin j a acestei tensiuni are expresia (2.11). Insumand
armonicile spatiale de ordin j determinate
de toate bobinele, se obtine armonica spatiala rezultanta
de expresie:
unde amplitudinea 
are o expresie care
depinde de constructia infasurarii si difera de
la caz la caz.
Expresia (2.19) a armonicii spatiale de ordin j arata ca, in cazul constructiilor nesimetrice, armonica fundamentala este armonica j=p; pentru armonicile de ordin j<p se obtin armonici fractionare, iar pentru armonicile de ordinul j care nu sunt multiplul numarului de perechi de poli p se obtin armonici fractionare superioare. Aceste cazuri particulare sunt tratate separat in literatura de specialitate.
a. Breviar
|
In constructiile uzuale infasurarile monofazate sunt astfel executate incat se asigura aceeasi curba de variatie a tensiunii magnetice pentru doua perechi de poli magnetici succesivi; Daca bobinele
sunt identice pentru toti polii magnetici tensiunea magnetica
rezultanta in intrefier produsa de o infasurare
monofazata alimentata cu un curent sinusoidal (2.6) este o
functie alternativ periodica cu perioada In cazul in care axa spatiala de referinta se suprapune peste axa magnetica a infasurarii (vezi figura 2.15), expresia armonicii spatiale de ordin j a tensiunii magnetice este (2.18): unde Daca axa magnetica a
bobinei este decalata inainte cu unghiul unde amplitudinea |
|
Politica de confidentialitate | Termeni si conditii de utilizare |
Vizualizari: 904
Importanta: 
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved
(2.20) 
(2.20.a) 
fata de
axa spatiala, atunci expresia armonicii spatiale de ordin j
este:
(2.20.b) 
a armonicii j este
exprimata de relatia (2.18.a).