| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
Fundamentarea primelor si a rezervei matematice la asigurarile de viata
1. Asigurarile de viata si calculul probabilitatilor
Asigurarile moderne au trecut la practica primelor fixe. Aplicarea unui astfel de sistem presupune baze sanatoase pentru calcularea acestora.
Intrarea in aceasta faza a fost usurata:
de tinere de statistici privind producerea riscurilor;
de dezvoltare a acelei ramuri din stiintele matematice care se ocupa cu calculul probabilitatilor.
In asigurari nu se lucreaza cu probabilitati ideale. In constituirea tarifelor de prime se iau in vedere datele statistice care reprezinta probabilitati ideale corectate cu abaterile.
In asigurarile de persoane sunt numerosi factori care determina abateri:
varsta;
sexul;
starea matrimoniala;
antiselectia;
profesia;
regiunea geografica;
clima.
De-a lungul timpului, diferitele societati de asigurari si-au intocmit pentru necesitati proprii, tabele de probabilitate a ivirii unor riscuri. Un loc aparte intre acestea pentru asigurarile de viata il ocupa tabelele de mortalitate ale asiguratilor. Pe langa acestea, asiguratorii au intocmit si tabele de invaliditate si de morbiditate.
Societatile de asigurari construiesc astfel de tabele pe baza deceselor, a invaliditatii si a bolilor produse in randul asiguratilor.
Cu ocazia intocmirii recensamintelor populatiei, tarile intocmesc tabele de morbiditate generale a populatiei, pe care le folosesc in diferite lucrari cu caracter demografic. Asemenea tabele se folosesc si de institutiile de asigurare.
Ele cuprind o serie de indicatori:
- lx = numarul supravietuitorilor de varsta x si arata cate persoane din generatia ipotetica de 100.000 nascuti vii mai sunt in viata la implinirea varstei de x ani.
- dx = numarul decedatilor intre varstele x si x+1 ani si arata cate persoane dintre supravietuitorii varstei x mor inainte de a implini x+1 ani, adica in cursul anului considerat.
- qx = probabilitatea de moarte intre x si x+1 ani si arata riscul la care e supusa o persoana care a implinit x ani sa inceteze din viata inainte de a implini x+1 ani.
- px = probabilitatea de supravietuire intre x si x+1 ani si arata sansele pe care le are o persoana care a implinit x ani sa fie in viata la implinirea a x+1 ani
- lmx = numarul mediu al supravietuitorilor intre x si x+1 ani.
- Ex = speranta de viata la varsta x si indica numarul mediu de ani ramasi de trait pentru o persoana care supravietuieste varstei de x ani.
dx
= lx - lx+1 ![]() ;
; ![]()
![]()
![]()
![]() = varsta la care moare ultimul supravietuitor ( la noi
100).
= varsta la care moare ultimul supravietuitor ( la noi
100).
Eox = speranta de viata la nastere, denumita durata medie de viata
indica numarul mediu de ani pe care poate sa-i traiasca un nou-nascut in conditiile intensitatii mortalitatii pe varste din perioada de referinta a tabelei de mortalitate.
dx = lx - lx+1
![]() ;
; ![]() ;
; ![]()
![]()
![]() probabilitatea ca o
persoana de x ani sa fie in viata peste n ani (lx
= numarul supravietuitorilor la varsta x).
probabilitatea ca o
persoana de x ani sa fie in viata peste n ani (lx
= numarul supravietuitorilor la varsta x).
E de precizat ca indicatorii de supravietuire, respectiv de moarte sunt variabili pentru colectivitaea privita in ansamblul ei, dar ei pot varia de la o persoana la alta.
Societatile de asigurare urmaresc mortalitatea si pe sexe. Observarile au condus la concluzia ca mortalitatea, indeosebi dupa 50 de ani, e simtitor mai crescuta la barbati. Aceasta constatare justifica introducerea unor prime diferentiate pe sexe, mai ales la asigurarile viagere de pensii in sensul ca primele la asigurarile de pensii ale femeilor sunt mai mari intrucat bucurandu-se de o longevitate mai mare vor primi implicit pensii un numar de ani mai mare decat barbatii.
S-a studiat si dinamica mortalitatii in functie de starea matrimoniala, constatandu-se fenomene interesante. Pentru barbati, cel mai scazut grad de mortalitate se constata la cei casatoriti. Mortalitatea creste simtitor la celibatari, pentru ca la vaduvi si la divortati, indicele de mortalitate sa fie si mai mare. O dinamica de sens asemanator, desi gradele difera, se constata si la femei.
Profesiile au si un cuvant de spus in privinta mortalitatii. Societatiile care practica asigurari de viata nu fac grupaje deosebite in functie de acestea. In practica asigurarilor de accidente insa, profesia asiguratorului joaca un rol hotarator. Astfel, profesiile sunt impartite in 4-6 grupe, categoriile tarifare cu prime crescande de la categoria I spre categoria IV, respectiv VI, in ordinea cresterii periculozitatii.
Constatari interesante rezulta si din studiul influentei regiunii geografice si a climei asupra mortalitatii. In aceeasi tara, oamenii de la munte traiesc mai mult decat cei de la campie, si cei de la campie mai mult decat cei din zona de delta, datorita frecventei diferentiate a germenilor patologici. Mortalitatea in mediul rural e mai scazuta decat in cel urban, mentinandu-se pe sexe la varste mai inaintate, diferente de mortalitate in favoarea femeilor.
Influenta climei e de asemenea puternica. Populatia din zona temperata traieste mai mult decat cea din zona tropicala si poli. Persoanele care se deplaseaza de la un climat la altul, sensibil schimbat, au dificultati de adaptare, ceea ce trebuie sa stea in atentia asiguratorului.
Influenta
antiselectiei nu poate trece neobservata. Statisticile arata
ca in asigurarile de deces, mortalitatea la persoanele de toate
varstele e mai ridicata decat mortalitatea generala si mortalitatea
celor care incheie asigurari de viata ![]() in ciuda
examinarii medicale ceruta in unele cazuri la asigurarile de
deces, totusi persoanele care aleg asigurarile de deces si
izbutesc sa o incheie, au o stare a sanatatii mai
putin buna decat cele ce nu incheie asigurari sau incheie
asigurari de viata.
in ciuda
examinarii medicale ceruta in unele cazuri la asigurarile de
deces, totusi persoanele care aleg asigurarile de deces si
izbutesc sa o incheie, au o stare a sanatatii mai
putin buna decat cele ce nu incheie asigurari sau incheie
asigurari de viata.
Eficacitatea selectiei pe care asiguratorul o face prin reglementari sau examinare medicala e mai slaba decat cea a antiselectiei pe care o practica asiguratii.
2.Fructificarea fondurilor de asigurare
O particularitate a asigurarilor de viata o constituie perioada indelungata de 5-20 sau mai multi ani pentru care se incheie. In perioada respectiva, asiguratul plateste prime de asigurare, iar asiguratorul se angajeaza sa achite suma asigurata in caz de deces al asiguratului sau la expirarea asigurarii in caz de supravietuire a acestuia. Pentru a-si putea onora obligatiile asumate, asiguratorul isi creaza pe baza primelor incasate un anumit fond care, mentinut in circuitul economic, produce venit. Acest venit se ia in calcul atunci cand se stabileste marimea primei de asigurare. Venitul realizat de asigurator depinde de:
- marimea sumei varsate la fond;
- durata pastrarii acestora in circuitul economic;
- modul de fructificare.
![]() C0 - suma initiala C C C Cn
C0 - suma initiala C C C Cn
n - numarul de ani 0 1 2 3 n
r - rata de actualuzare ( const.)
Cn = ?
Cn = C0 ( 1+ r)n = C0 un 1+r = u - facctor de compunere simpla
![]()
![]() - factor de disccontare
simplu
- factor de disccontare
simplu
L0 - prima de asigurare
Ln - suma asigurata
n - durata asigurarii
r - rata de fructificare
3. Prima neta umica la asigurarile de viata
Avem asigurari:
I. de supavietuire (de capitalizare) care dupa modalitatea de plata sunt: 1.cu plata forfetara (o singura data) a Sa;
2.cu plata Sa sub forma de rente (anuale) care dupa durata de achitare a rentelor sunt: a) asigurari de rente viagere
b) asigurari de rente amanate i) anticipate (la inc. anului)
![]()
c) asigurari de rente temporare ii) posticipate (la sf. anului)
d) asigurari amanate temporare
II.de deces (protectie): 1. asigurari viagere
2. asigurari amanate
3. asigurari temporare
4. asigurari amanate temporar
III.mixte de viata: - cu plata forfetara a Sa
![]() combinatia lor.
combinatia lor.
- asigurari temporare de deces
Prima neta unica la asigurarile de supravietuire
1. Plata forfetara unica a Sa
vn
![]() lx 1-lx+n
lx 1-lx+n
![]()
n
x x+n
momentul subscrierii politei de asigurare ; x -varsta ; lx - incheie asigurarea (sunt in viata) ; la momentul n sunt in viata lx+n ; peste n ani achita 1 u.m. lx+n ; Sa = 1 u.m.
se achita in prezent
discontare: ![]()
angajamentul prezent: 1lx+n-vn
prima neta unica pentru
un singur asigurat: ![]()
![]()
![]() probabilitatea ca
persoana care incheie azi asigurarea de x ani, sa fie in viata
peste n ani.
probabilitatea ca
persoana care incheie azi asigurarea de x ani, sa fie in viata
peste n ani.
![]()
![]()
lx vn = Dx - primul numar de comutatie la asigurarile de supravietuire
2.a.i. Prima neta unica la asigurarile de rente viagere anticipate
lx lx+1 lx+2 l
![]()
0 1 2 ω ω = 100 - la care moare ultimul supravietuire
![]()
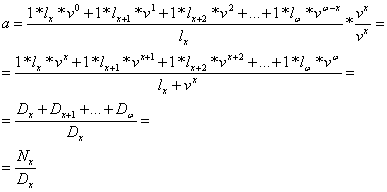
![]()
![]() prima unica
unitara
prima unica
unitara
![]()
![]()
al doilea numar de comutatie de la asigurarile de supravietuire
![]() , daca Sa
≠ 1 Sa
- suma asig. a rentei
, daca Sa
≠ 1 Sa
- suma asig. a rentei
![]() - prima neta
anuala
- prima neta
anuala
2.a.ii. Prima neta unica la asigurarile de rente viagere posticipate
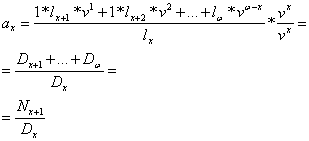 , pentru Sa
= 1
, pentru Sa
= 1
![]() , pentru Sa
≠ 1
, pentru Sa
≠ 1
diferenta e ca la cele
anticipate ![]() > cu o renta
> cu o renta
2.b.i. Prima neta unica la asigurarile de rente amanate anticipate
![]() lx lx m l
lx lx m l
m ω
x x+m
![]()
m
m - durata
amanarii platii rentelor (de la anul m asiguratorul incheie in
fiecare an renta![]() deces)
deces)
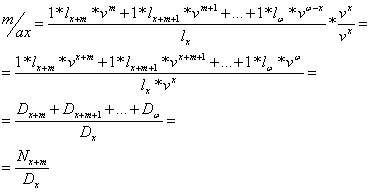
![]() ex. m = 39
la asigurarile de pensii
ex. m = 39
la asigurarile de pensii
2.c.i. ![]() la asigurarile de
rente temporare anticipate
la asigurarile de
rente temporare anticipate
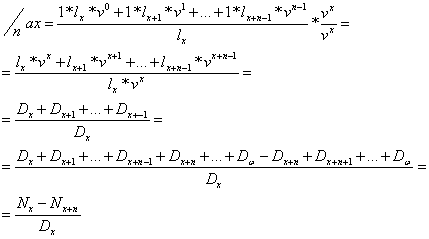
![]()
n - durata achitarii rentelor
- din primul an asiguratul plateste renta
- plata incepe din anul subscrierii
- ultima plata la inceputul anului n ( sfarsitul anului n-1)
2.c.ii.![]() la asigurarile de rente temporare posticipate - ultima plata
la sfarsitul anului n
la asigurarile de rente temporare posticipate - ultima plata
la sfarsitul anului n
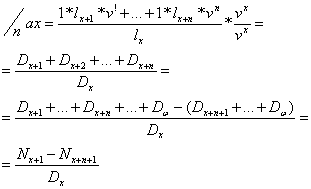
![]() ; Ex.la
barbatii ce au un copil in afara casatoriei, in loc de
pensie alimentara.
; Ex.la
barbatii ce au un copil in afara casatoriei, in loc de
pensie alimentara.
2.d.i.![]() la asigurarile de rente amanate-temporare anticipate
la asigurarile de rente amanate-temporare anticipate
- trebuie sa treaca multi ani de la incheierea asigurarii ca timp de n ani sa fie achitata de asigurator
- ultima plata se face pentru lx+m+n-1 supravietuitori
lx lx+m lx+m+n
![]()
![]() m m+n
m m+n
n
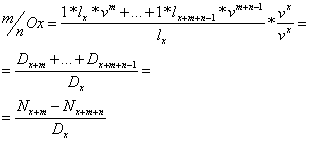
![]()
Ex.asigurarea pentru un copil de 10 ani pentru ca la 18 ani si timp de 5 ani asiguratorul ii achita renta.
2.d.ii. ![]() la asigurarile de
rente amanate-temporare posticipate - prima plata din m+1
la asigurarile de
rente amanate-temporare posticipate - prima plata din m+1
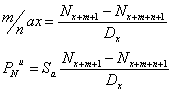
3.2. Prima neta unica la asigurarile de deces
1)
![]() la asigurarile
viagere de deces
la asigurarile
viagere de deces
![]() - Sa merg la beneficiari
- Sa merg la beneficiari
![]() dx - numarul
de persoane ce decedeaza in (x, x+1) lx
dx - numarul
de persoane ce decedeaza in (x, x+1) lx
![]() v0 - nu trece
primul an
v0 - nu trece
primul an
ω - moare ultimul 0 1 2 ω
pentru
Sa = 1 ![]()
![]()
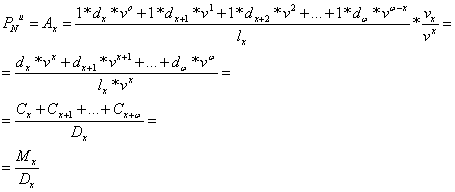
dx * vx = Cx - primul numar de comutatie de la deces
![]()
![]() - al doilea numar de comutatie de la deces
- al doilea numar de comutatie de la deces
![]()
2)
![]() la asigurarea amanata de deces + trec cei m ani si
numai dupa cei m ani decesul are loc, asiguratorul plateste.
la asigurarea amanata de deces + trec cei m ani si
numai dupa cei m ani decesul are loc, asiguratorul plateste.
![]() ,
, ![]()
3)
![]() la asigurarea temporara de deces
la asigurarea temporara de deces
![]() ,
, ![]()
4)
![]() la asigurarile
amanate-temporare de deces
la asigurarile
amanate-temporare de deces
![]()
![]()
3.3. ![]() la asigurarile
mixte de viata
la asigurarile
mixte de viata
- pentru Sa ![]()
- pentru Sa ![]()
4. Prima neta anula la
asigurarile de viata ![]()
k = durata de plata a ratelor anuale de prima
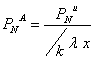 ; k ≤ n ;
; k ≤ n ; ![]() x - anuitatea anticipata limitata la k
x - anuitatea anticipata limitata la k
4.1. ![]() la asigurarile de
supravietuire
la asigurarile de
supravietuire
1. ![]() la asigurarile de
supravietuire cu plata forfetara a Sa
la asigurarile de
supravietuire cu plata forfetara a Sa
![]()
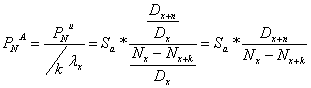
2.a.i. ![]() la asigurarile de
rente viagere anticipate
la asigurarile de
rente viagere anticipate
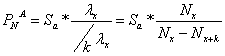
2.a.ii.![]() la asigurarile de rente viagere posticipate
la asigurarile de rente viagere posticipate
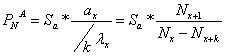
2.b.i.![]() la asigurarile de rente amanate anticipate
la asigurarile de rente amanate anticipate
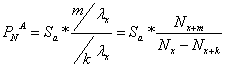
2.b.ii.![]() la asigirarile de rente amanate posticipate
la asigirarile de rente amanate posticipate
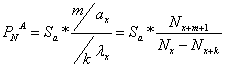
2.c.i. ![]() la asigurarile
temporare anticipate
la asigurarile
temporare anticipate
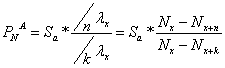
2.c.ii. ![]() la asigurarile de
rente temporare posticipate
la asigurarile de
rente temporare posticipate
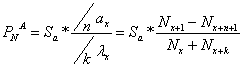 ; ax -
; ax - ![]() unitata
unitata
m - amanata
n - limitata
2.d.i. ![]() la asigurarile de
rente amanate - temporare anticipate
la asigurarile de
rente amanate - temporare anticipate
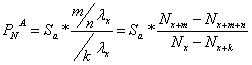
2.d.ii. ![]() la asigurarile de
rente amanate - temporare posticipate
la asigurarile de
rente amanate - temporare posticipate
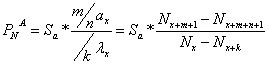
4.2. ![]() la asigurarile de
deces
la asigurarile de
deces
1.![]() la asigurarea viagera de deces
la asigurarea viagera de deces
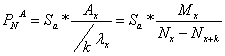
2. ![]() la asigurarea
amanata de deces
la asigurarea
amanata de deces
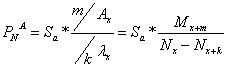
3. ![]() la asigurarea
temporara de deces
la asigurarea
temporara de deces
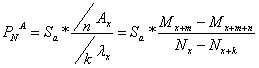
4. ![]() la asigurarea
amanata - temporara de deces
la asigurarea
amanata - temporara de deces
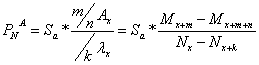
4.3. ![]() la asigurarea
mixta de viata
la asigurarea
mixta de viata
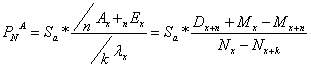
5. Determinarea primei comerciale (brute) unice la asigurarile de viata
Prima bruta unica
- pentru Sa = 1 u.m. ![]()
Ca = cheltuieli de achizitie (cheltuieli cu contractarea asigurarii)
comisionul agentului
cheltuieli cu examinarea medicala a asiguratului
cheltuieli cu publicitatea
cheltuieli cu formularele si cu introducerea in baza de date
![]() Ca = L * Sa
Ca = L * Sa
"L" - coeficientul cheltuielilor de achizitie a asigurarii
![]()
Ci - coeficient de incasare a primelor
![]() - coeficientul cheltuielilor de incasare a primelor
- coeficientul cheltuielilor de incasare a primelor
Cg -cheltuieli de gestiune ale asiguratorului
- ![]() = ch. de gestiune ale
asiguratorului aferente duratei de incasare a primelor (k)
= ch. de gestiune ale
asiguratorului aferente duratei de incasare a primelor (k)
- ![]() = ch. de gestiune ale
asiguratorului aferente duratei asigurate (n)
= ch. de gestiune ale
asiguratorului aferente duratei asigurate (n)
- ![]() = coef. ch. anuale de
gestiune ale asiguratorului aferente duratei k
= coef. ch. anuale de
gestiune ale asiguratorului aferente duratei k
- ![]() = coef. ch. anuale de
gestiune ale asiguratorului aferente duratei asigurate (n)
= coef. ch. anuale de
gestiune ale asiguratorului aferente duratei asigurate (n)
![]()
![]()
- pentru Sa
= 1u.m. , 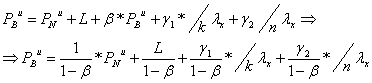
Determinarea primei brute (comerciale) anuale la asigurarile de viata
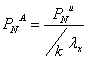 ;
; 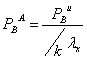
- pentru Sa
= 1u.m. 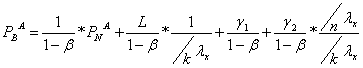
![]() (1 u.m.) - prima
anuala
(1 u.m.) - prima
anuala
varianta 1 - semestrial
![]() (1+0,02) cS = 2% comision
(1+0,02) cS = 2% comision
varianta 2 - trimestrial
![]() (1+0,03) cT =
3%
(1+0,03) cT =
3%
varianta 3 - lunar
![]() (1+0,05) cL
= 5%
(1+0,05) cL
= 5%
pentru plata cherabila a ratelor de prima: comision cCH = 10%
![]()
v1). ![]()
v2). ![]()
v3). ![]()
6. Determinarea rezervei matematice la asigurarile de viata
Rezerva matematica = diferenta dintre valoarea actuariala a obligatiilor financiare ale asiguratorului si valoarea actuariala a obligatiilor financiare ale asiguratului.
Rezerva matematica teoretica (Rt)
![]() Metoda prospectiva n-t
Metoda prospectiva n-t
Rt
![]()
0 1 2 t n
x+t x+n
Rt = VAtOA - VAtOa
VAtOA = valoarea actualizata actuariala la momentul t a obligatiilor financiare ale asiguratorului;
VAtOa = valoarea actualizata si actuariala la momentul t a obligatiilor financiare ale asiguratului.
![]() - pentru n = k VAtOa =
- pentru n = k VAtOa = ![]()
![]()
VAtOA
= Sa * ![]()
![]()
![]() exigibilitate
exigibilitate
Metoda retrospectiva
![]() t Rt
t Rt
![]()
0 1 2 t n
x+t x+n
la momentul "0" VAtOA = VAtOa =0
la momentul
"t" VAtOa = ![]() Rt < Sa
Rt < Sa
VAtOA
= ![]()
VAtOa
= VAtOa = VAtOA 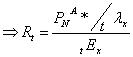
Rezerva matematica practica la asigurarile de viata prin metoda prospectiva
![]() Rt = VAtOA - VAtOa k-t
Rt = VAtOA - VAtOa k-t
Situatia
1: t![]() ( 0,k) S1 Rt S2 Rt
( 0,k) S1 Rt S2 Rt
![]() VAtOa =
VAtOa = ![]() 0 t k n
0 t k n
x+t
![]() n-t
n-t
VAtOA
= Sa* ![]()
![]()
![]()
![]()
Situatia
2: t ![]() (k,n) ; Ci
= 0 ;
(k,n) ; Ci
= 0 ; ![]()
VAtOa
= 0 ![]() Rt = VAtOA
Rt = VAtOA
VAtOA
= Sa =![]()
7. Stabilirea valorilor de rascumparare
pentru t creste spre 10 VR =95% Rt - valoarea de rascumparare pentru reziliere <
pentru t ≥ 10 VR = Rt - valoarea de rascumparare pentru reziliere ceruta dupa un nr. de ani ≥ 10
8. Determinarea sumei de asigurare reduse la asigurarile de viata (S.a.r.)
Rt
= ![]() - rezerva se
transforma in
- rezerva se
transforma in ![]()
Rt
= ![]() (1 u.m.)
(1 u.m.) ![]()
Pentru
asigurarea mixta de viata:![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2040
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved