| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
TEORIA CONSUMATORULUI
1. De ce mai intai consumatorul?
Dupa cum s‑a retinut din cursurile introductive, analiza microeconomica este dedicata explicarii comportamentelor individuale si interactiunilor lor. In centrul atentiei este situat deci nivelul individual, reprezentat de omul aflat intr‑o permanenta cautare a satisfacerii nevoilor sale. El este privit in dubla sa ipostaza, de consumator si de producator. In calitate de consumator, individul se manifesta ca purtator al cererii de bunuri si servicii de consum, urmarind maximizarea satisfacerii nevoilor sale prin utilizarea resurselor limitate pe care le are la dispozitie. Altfel spus, el cauta maximizarea utilitatii economice, pe baza principiului hedonist*.
In calitate de producator, individul se manifesta ca purtator al ofertei de bunuri si servicii, pe care o produce prin combinarea factorilor de productie, de fapt, prin consumarea acestora. Ca agent esential al productiei, dar si al pietei, producatorul, cunoscut si sub numele de intreprinzator, urmareste maximizarea rezultatelor obtinute, concretizate in diferenta dintre veniturile incasate prin vanzarea bunurilor produse si cheltuielile efectuate cu factorii de productie consumati.
Orice producator este insa in acelasi timp si consumator. El trebuie sa‑si satisfaca si multitudinea nevoilor sale, ca oricare alt individ. Nu putem spune acelasi lucru si despre consumatorul purtator al cererii, intrucat exista largi categorii ale populatiei care sunt consumatoare de bunuri si servicii fara a fi in acelasi timp si producatoare ale acestora. Acesta este unul din motivele pentru care incepem analiza microeconomica prin studierea comportamentului consumatorului. In plus, exista numeroase similitudini intre comportamentul consumatorului si cel al producatorului, elemente din primul manifestandu‑se in forme transformate in cel de‑al doilea, asa cum se va evidentia dupa studierea celor doua tipuri fundamentale de comportament.
Teoria consumatorului isi propune sa explice maniera in care individul repartizeaza resursele sale intre diferite bunuri si servicii disponibile, astfel incat sa‑si maximizeze satisfactia produsa prin consumul lor. Obtinerea satisfactiei maxime oferite de consumul bunurilor si serviciilor procurate cu ajutorul resurselor limitate care formeaza 'bugetul' individului defineste starea de echilibru a consumatorului. Aceasta teorie a fost dezvoltata de economistii neoclasici din ultima patrime a secolului al XIX‑lea**, sub influenta filosofilor utilitaristi, pornindu‑se de la premisa ca individul rational cauta maximum de satisfactie sau de utilitate.
2. Abordarea cardinala a utilitatii si echilibrul consumatorului
In conceptia clasica, bunuri identice au, pentru persoane diferite, aceeasi utilitate economica, indiferent de intensitatea nevoilor, de cantitatea consumata si de sacrificiul facut pentru obtinerea lor, astfel incat unitatile X1, X2, .., Xn dintr‑un bun omogen au utilitatile individuale u1, u2, .. , un, egale intre ele, utilitatea totala a intregii cantitati fiind n u.
In realitate insa, nivelul de satisfactie obtinut prin consumul unui bun difera nu numai de la individ la individ, ci si de la o unitate la alta consumata din acelasi produs. Acest fapt rezulta din gradul diferit de intensitate al nevoii satisfacute prin consumul bunului respectiv, care descreste pe masura ce sporeste numarul de unitati consumate. Pornind de aici, economistii neoclasici au fundamentat in ultima patrime a secolului al XIX‑lea teoria utilitatii marginale. Intr‑o prima forma, a asa‑numitei 'abordari cardinale', s‑a presupus ca individul este capabil sa masoare printr‑un indice cantitativ precis utilitatea pe care o obtine din consumul fiecarei unitati dintr‑un anumit bun omogen. De aici a rezultat posibilitatea stabilirii unei ierarhii intre nivelurile de utilitate si a exprimarii numerice a satisfactiei oferite de consumul unei anumite cantitati dintr‑un bun, comparativ cu cea data de folosirea unei cantitati dintr‑un alt bun. Cu toate ca teoria utilitatii cardinale a fost respinsa si depasita, o serie de concepte si instrumente de analiza fundamentate in cadrul ei au ramas in patrimoniul stiintei economice, motiv pentru care le prezentam in continuare.
2.1. Utilitatea totala si utilitatea marginala
Utilitatea totala, U, a unui bun oarecare, X, masoara satisfactia globala pe care individul o obtine prin consumarea unei anumite cantitati din acest bun. Deci, nivelul lui U depinde de cantitatea consumata, adica 'U este functie de X', ceea ce se scrie: U = f(x), in care X este cantitatea consumata din bunul X.
Pentru a determina sensul si ritmul in care utilitatea totala evolueaza atunci cand cantitatea consumata din bunul X creste, se foloseste conceptul de utilitate marginala. Utilitatea marginala, Um, masoara evolutia utilitatii totale pentru o variatie foarte mica a cantitatii consumate.
In tratarea utilitatii marginale distingem doua cazuri:
a) Utilitatea marginala a unui bun partial sau imperfect divizibil. Spunem ca un bun este imperfect divizibil daca exista o unitate de masura dincolo de care este imposibil de coborat (de exemplu, un consumator nu poate utiliza trei sferturi de automobil sau jumatate de ochelari; automobilul si ochelarii sunt bunuri imperfect divizibile).
Utilitatea marginala a unui bun X imperfect divizibil (UmX) reprezinta variatia utilitatii totale (U) determinata de consumul unei unitati suplimentare din acest bun.
deci: ![]() (1.)
(1.)
b) Utilitatea marginala a unui bun perfect divizibil
Daca bunul X este perfect divizibil, atunci oricare ar fi unitatea de masura folosita, exista mereu o cantitate mai mica ce poate fi consumata. De exemplu, daca masuram consumul in grame, un gram nu reprezinta consumul 'marginal', deoarece acesta poate fi marit cu 0,5 grame. Nici atunci cand folosim ca etalon jumatatea de gram, aceasta nu poate reprezenta un consum marginal, deoarece putem utiliza mereu un etalon de masura mai mic: 0,25 grame, un miligram sau submultipli mai mici. In acest caz, o definitie riguroasa a utilitatii marginale trebuie sa ia in considerare evolutia utilitatii totale, care rezulta dintr‑o variatie infinit de mica a consumului bunului X.
Deci, putem spune ca utilitatea marginala a unui bun perfect divizibil reprezinta variatia utilitatii totale pentru o variatie infinit de mica ('infinitezimala') a cantitatii consumate din acel bun.
Exprimarea utilitatii
marginale astfel definite se poate realiza cu ajutorul conceptului matematic de
derivata. Sa ne reamintim ca derivata unei variabile oarecare y, care este
functie de o alta variabila x, masoara cum variaza y pentru o variatie a lui x
care tinde spre zero. Daca y = f(x), putem scrie derivata lui y in functie de x
in doua maniere: y'(x) sau ![]() .
Deci, din punct de vedere matematic, utilitatea marginala a unui bun perfect
divizibil reprezinta derivata functiei de utilitate totala in raport cu X, adica:
.
Deci, din punct de vedere matematic, utilitatea marginala a unui bun perfect
divizibil reprezinta derivata functiei de utilitate totala in raport cu X, adica:
Um = f ' (x) sau Um=![]() (2.)
(2.)
2.2. Evolutia utilitatii totale si a utilitatii marginale
Am vazut doar ca utilitatea totala a unui bun oarecare masoara satisfactia globala obtinuta de individ prin consumarea unei anumite cantitati din bunul respectiv. Cum evolueaza insa nivelul de satisfactie a individului atunci cand el consuma o cantitate crescanda dintr‑un bun? Va creste proportional cu cantitatea consumata suplimentar, cum am fi tentati sa credem? Intrucat satisfactia reprezinta de fapt placerea oferita de consum, care este opusul nemultumirii provocate de lipsa unui anumit bun necesar satisfacerii unei nevoi, raspunsul corect la intrebarea de mai sus este: nivelul de satisfactie obtinut prin consumul unei cantitati crescande dintr‑un bun depinde de intensitatea nevoii pe care consumatorul cauta s‑o satisfaca; placerea nu este proportionala cu cantitatea consumata, ci cu lipsa, cu nemultumirea incercata inaintea consumului. In acest sens, analiza economica se foloseste de o ipoteza simpla: intensitatea unei nevoi este descrescanda pe masura ce cantitatea consumata creste. Acesta este principiul intensitatii descrescande a nevoilor, formulat de psihologul german Heinrich Gossen, in anul 1843, din care s‑a ajuns la principiul utilitatii marginale descrescande: utilitatea suplimentara oferita de consumul unei cantitati crescande dintr‑un anumit bun descreste pana cand devine nula la punctul de saturatie.
Daca intensitatea nevoii descreste odata cu cresterea cantitatii consumate, satisfactia, adica utilitatea, obtinuta pentru fiecare unitate consumata suplimentar este mai mica decat pentru precedenta. De exemplu, intr‑o zi caniculara de vara, intensitatea nevoii de a bea racoritoare pentru a potoli setea este foarte ridicata. Primul pahar de racoritoare consumat satisface o nevoie de intensitate maxima. Al doilea pahar consumat procura mai putina satisfactie sau placere decat primul, iar al treilea mai mica decat al doilea s.a.m.d. Atentie insa! Aceasta nu inseamna ca satisfactia totala se diminueaza. Dimpotriva, ea creste, dar cu o ratie descrescanda. Daca individul continua sa bea (intrucat ii face placere), utilitatea totala continua sa creasca, dar din ce in ce mai putin repede, adica utilitatea marginala se diminueaza.
Considerand bautura
racoritoare ca fiind bunul X, paharele baute succesiv x1, x2,
, xn, iar utilitatea corespunzatoare fiecarui pahar U1, U2,
, Un, Ui (i =
1,2,..,n) reprezinta utilitatile individuale cu proprietatea ca U1>U2
>Un; Un reprezinta utilitatea marginala, iar ![]() reprezinta
utilitatea totala.
reprezinta
utilitatea totala.
Cele de mai sus pot fi evidentiate si printr‑o reprezentare grafica, asa ca in figura 1. Pe ordonatele celor doua grafice inscriem nivelul utilitatii totale (U), respectiv al utilitatii marginale (Um), iar pe abscise inscriem cantitatea consumata din bunul considerat (X). U poate fi deci reprezentata, printr‑o curba crescatoare, iar Um printr‑o curba descrescatoare. U atinge nivelul sau maxim in punctul S, numit punctul de satietate sau de saturatie a consumatorului.
|
In acest punct, Um este nula,adica o unitate suplimentara de consum nu mai sporeste satisfactia. Daca individul si‑ar mari consumul dincolo de acest punct, utilitatea marginala ar deveni negativa, ceea ce ar face ca si utilitatea totala sa inceapa a se micsora. Deci, un consum exagerat dintr‑un anumit bun poate antrena nu o crestere a satisfactiei, ci, dimpotriva, o insatisfactie, o suferinta chiar. De exemplu, daca primele pahare de bautura racoritoare ar fi agreabile pentru un individ intr‑o zi calduroasa de vara, nu acelasi lucru s‑ar intampla pentru al douazecilea pahar. |
|
Intrucat insa una dintre ipotezele fundamentale ale stiintei economice este rationalitatea, vom presupune ca individul rational nu‑si va continua consumul dincolo de punctul de satietate, astfel incat utilitatea marginala va fi in mod normal descrescatoare si pozitiva.
Evolutia utilitatii totale si a celei marginale poate fi la fel de sugestiv prezentata si prin graficul din fig. 2. de mai jos:
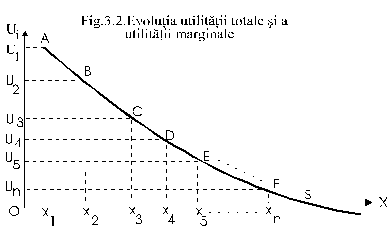
Se observa ca fiecarei unitati xi din bunul X ii corespunde o utilitate individuala Ui (i=1,2,., n). Daca se consuma numai unitatea X1, utilitatea totala coincide cu utilitatea individuala si cu cea marginala. Daca se adauga unitatii x1, consumate, si unitatea x2, atunci Um devine U2, iar utilitatea totala va fi suma U1+U2, ceea ce pe grafic reprezinta suprafata marcata de axele de coordonate si curba AB. Daca vor fi consumate toate unitatile, de la x1 pana la xn, Um va fi Un (utilitatea celei de‑a n‑a unitati consumate), iar utilitatea totala va fi reprezentata de suprafata cuprinsa intre axele de coordonate si curba ABCDEF, care descrie de fapt evolutia utilitatii marginale.
2. Alegerea optimala a consumatorului
Fiind nevoit sa‑si satisfaca numeroase nevoi, individul alege din varietatea bunurilor care‑l inconjoara acele combinatii care‑i pot oferi cea mai mare satisfactie. Deci, consumatorul rational cauta sa‑si maximizeze utilitatea.
Intr‑o ipotetica situatie de abundenta, nimic nu limiteaza posibilitatile de consum ale individului. El nu suporta nici un cost, nu trebuie sa consimta nici un sacrificiu pentru a‑si procura o cantitate oarecare dintr‑un bun. De aceea, poate consuma orice bun pana in momentul in care utilitatea totala este maxima, fapt care se intampla atunci cand utilitatea marginala devine nula. Deci, conditia alegerii optimale a consumatorului, denumita si conditia de echilibru a consumatorului, in situatia de abundenta este:
![]() ()
()
In realitate,
bunurile care ne satisfac trebuintele prin consum sunt rare. De aceea individul
trebuie sa aleaga intre mai multe posibilitati de consum. In situatia
de raritate a unei economii de troc, deci unde bunurile se schimba
direct intre ele, a consuma un bun X inseamna a renunta la un bun Y sau la un bun
Z, sau la oricare altul pe care l‑ai fi putut obtine in schimb. Inseamna
ca bunul X are un cost de oportunitate, reprezentat de satisfactiile pe care le‑ar
putea obtine individul renuntand la consumul lui X. De aceea, individul nu‑si
mai poate continua consumul pana la punctul de saturatie. Daca presupunem ca
exista numai doua bunuri substituibile, X si Y, combinatia optimala care‑i
asigura consumatorului maximizarea satisfactiei este cosul (X, Y) astfel
determinat incat utilitatea marginala a celor doua bunuri sa fie egala. Daca ![]() ,
consumatorul si‑ar mai putea spori utilitatea totala substituind unei
unitati din Y o unitate din X si continuand aceasta substituire atat timp cat
,
consumatorul si‑ar mai putea spori utilitatea totala substituind unei
unitati din Y o unitate din X si continuand aceasta substituire atat timp cat ![]() .
In acest caz, cum stim ca utilitatea marginala este descrescanda in raport cu
cantitatea consumata,
.
In acest caz, cum stim ca utilitatea marginala este descrescanda in raport cu
cantitatea consumata, ![]() va descreste, iar
va descreste, iar ![]() va creste, intrucat se diminueaza cantitatea
consumata din Y ca urmare a substituirii. Se ajunge astfel la un punct al
substituirii unde cele doua utilitati marginale devin egale. Dincolo de acest
punct,
va creste, intrucat se diminueaza cantitatea
consumata din Y ca urmare a substituirii. Se ajunge astfel la un punct al
substituirii unde cele doua utilitati marginale devin egale. Dincolo de acest
punct, ![]() ,
ceea ce ar determina necesitatea unei substituiri in sens invers, adica o
unitate din Y sa substituie o unitate din X pana la restabilirea egalitatii.
,
ceea ce ar determina necesitatea unei substituiri in sens invers, adica o
unitate din Y sa substituie o unitate din X pana la restabilirea egalitatii.
Deci, conditia de echilibru a consumatorului in situatia de raritate cu economie de troc este:
![]() (4)
(4)
2. In situatia de raritate
cu economie monetara, problema
consumatorului se schimba. Dispunand de o suma data, numita bugetul sau, individul
trebuie sa decida cum o imparte pentru procurarea bunului X si pentru
procurarea bunului Y. De aceasta data, el nu‑si va mai pune intrebarea
daca trebuie sa consume o unitate suplimentara din bunul X, sau din bunul
Y, pentru a‑si maximiza utilitatea,
ci daca trebuie sa cheltuiasca o unitate monetara suplimentara pentru bunul X
sau pentru bunul Y. Utilitatea maxima obtinuta prin cheltuirea sumei de care
dispune va fi atinsa atunci cand utilitatea marginala a unui leu cheltuit
pentru procurarea bunului X devine egala cu utilitatea marginala a unui leu
cheltuit pentru procurarea bunului Y. Utilitatea marginala pe o unitate
monetara cheltuita se obtine prin impartirea utilitatii marginale a bunului la
pretul sau. Daca ![]() si
si ![]() sunt preturile unitare ale bunurilor X,
respectiv Y, conditia de echilibru a consumatorului devine:
sunt preturile unitare ale bunurilor X,
respectiv Y, conditia de echilibru a consumatorului devine:
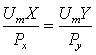 (5)
(5)
Demonstrarea acestei conditii se realizeaza printr‑un rationament similar celui folosit pentru situatia de raritate cu economie de troc.
2.4. Realizari si limite in abordarea cardinala a utilitatii
Meritul fundamental al teoreticienilor utilitatii marginale il constituie descoperirea unui principiu major al analizei microeconomice: adoptarea deciziilor individuale pe baza compararii si egalizarii costurilor si avantajelor aferente ultimei unitati consumate sau produse, care asigura maximizarea avantajelor (a utilitatii la teoria consumatorului sau a profitului la teoria producatorului).
De asemenea, pe baza luarii in considerare a utilitatii marginale s‑a putut oferi o solutie valabila problemei valorii. Este cunoscut faptul ca economistii clasici din secolele XVIII si XIX au intampinat serioase dificultati in reconcilierea valorii de intrebuintare si a valorii de schimb. Aparea o contradictie intre valoarea de intrebuintare, intemeiata pe utilitatea reprezentata de un bun pentru utilizatorul sau, si valoarea de schimb, exprimata prin pretul determinat pe piata. Aceasta problema a fost pusa de Adam Smith in 'Avutia natiunilor' si a ramas in literatura sub denumirea de 'paradoxul apei si diamantelor'. Apa, indispensabila vietii oamenilor, deci cu o utilitate foarte ridicata, nu valora nimic sau aproape nimic pe piata, in timp ce diamantele, mai putin necesare decat apa, au o valoare de schimb foarte ridicata. Paradoxul provenea din faptul ca se lua ca fundament al valorii utilitatea totala a bunului, in timp ce comportamentele individuale sunt ghidate de utilitatea marginala. Intr‑adevar, apa are o utilitate totala foarte mare. Utilitatea sa marginala este insa foarte scazuta, deoarece este abundenta, iar indivizii nu consimt sa faca sacrificii importante pentru a o obtine. In schimb, diamantele au o utilitate totala mai redusa decat a apei, fiindca sunt mai putin necesare, dar, fiind foarte rare, au o utilitate marginala mult mai ridicata si, in consecinta, un pret mult mai mare pe piata, indivizii consimtind astfel un sacrificiu important pentru a le obtine. Deci, observam ca daca se ia utilitatea marginala ca fundament al valorii, paradoxul dispare.
In pofida acestor realizari, in calea abordarii cardinale a utilitatii a ramas o dificultate insurmontabila: aceea a masurarii cantitative a utilitatii. Utilitatea este o notiune care depaseste sfera economicului pur, tine de psihologia consumatorului si are o conotatie morala, ce implica judecati de valoare, imposibil de apreciat prin cuantificari numerice. Consumatorul, atunci cand efectueaza alegerile, desi are in vedere diferentele cantitative de satisfactie date de dozele diferite de bunuri consumate, nu apeleaza la exprimari cifrice ale utilitatii, ci ierarhizeaza bunurile de care are nevoie in functie de ordinea preferintelor sale. Dupa cum preciza Ludwig von Mises, in aceasta privinta consumatorul nu cunoaste decat numarul ordinal si nu numarul cardinal .
Desigur, irealismul ipotezei cuantificarii utilitatii printr‑un indice cantitativ precis nu poate descalifica teoria utilitatii marginale ca instrument de cercetare stiintifica. Pentru depasirea obstacolului legat de aceasta ipoteza, reprezentantii de seama ai noii scoli marginaliste, in special Vilfredo Pareto si John Hicks, au formulat o ipoteza mai simpla si mai performanta: indivizii sunt capabili sa compare si sa clasifice alegerile conform unei ordini de preferinta, fara a mai atribui fiecareia un indice cantitativ, trecandu‑se astfel la abordarea ordinala a utilitatii si a echilibrului consumatorului.
Abordarea ordinala a utilitatii si echilibrul consumatorului
1. Axiomele teoriei alegerii
De aceasta data consumatorul stie sa faca alegerea bunurilor de care are nevoie nu prin masurarea utilitatii lor, ci prin stabilirea ordinei in care prefera bunurile respective. In fixarea combinatiilor posibile de produse de care are nevoie, numite 'cosuri' sau 'panere' de consum, consumatorul tine seama de doua elemente esentiale: valoarea relativa a produselor, adica preturile lor, si resursele banesti proprii disponibile pentru procurarea lor, care reprezinta ceea ce se numeste constrangerea sau restrictia bugetara.
Un 'cos' de consum
contine bunurile ![]() (i = 1, 2, 3, , m) iar fiecare bun are
unitatile
(i = 1, 2, 3, , m) iar fiecare bun are
unitatile ![]() (j = 1, 2, 3, ., n). Este evident ca exista
o infinitate de combinatii posibile intre bunurile care pot satisface nevoile
de consum, asa ca individul trebuie sa faca alegeri atat intre bunurile
(j = 1, 2, 3, ., n). Este evident ca exista
o infinitate de combinatii posibile intre bunurile care pot satisface nevoile
de consum, asa ca individul trebuie sa faca alegeri atat intre bunurile ![]() ,
cand pregateste 'cosurile', cat si intre 'cosurile'
,
cand pregateste 'cosurile', cat si intre 'cosurile' ![]() care asigura niveluri de utilitate diferita. Utilitatea
agregata, obtinuta prin consumul bunurilor din cosul
care asigura niveluri de utilitate diferita. Utilitatea
agregata, obtinuta prin consumul bunurilor din cosul ![]() ,
fie ele X, Y, Z, , s.a.m.d., este o functie de tipul U=u(X, Y,
Z,,s.a.m.d.).
,
fie ele X, Y, Z, , s.a.m.d., este o functie de tipul U=u(X, Y,
Z,,s.a.m.d.).
Pentru trierea alegerilor posibile si definirea unei ordini de preferinta in vederea construirii unei functii de preferinta, teoria alegerii pleaca de la urmatoarele axiome:
I. Relatia de comparatie sau de ordine completa: intre doua situatii posibile A si B, consumatorul o poate prefera pe A, ceea ce inseamna A > B, sau pe B, adica B > A, sau le poate considera echivalente, fiindu‑i indiferent daca o alege pe A sau B, ceea ce inseamna A = B. De aici rezulta ca individul poate stabili o ordine de preferinta pentru toate combinatiile sau 'cosurile' posibile.
II. Relatia de tranzitivitate: daca situatia A este preferata situatiei B, adica A>B, iar B este preferata situatiei C, adica B>C, atunci A este preferata situatiei C, adica A>C.
III. Relatia de non‑saturatie (sau cel mai mare este preferat celui mai mic): daca exista doua combinatii, A si B, ale acelorasi produse, ambele combinatii continand aceeasi cantitate din bunul X, dar combinatia B avand o cantitate mai mare din bunul Y, B este preferata combinatiei A, adica B>A.
IV. Relatia de continuitate (sau de indiferenta): presupunandu‑se existenta a doua combinatii, A si B, ca la axioma III, B va fi preferat lui A. Daca insa se va adauga la combinatia A cantitatea suplimentara din bunul Y necesara egalarii celei existente in combinatia B, consumatorul va ajunge intr‑o situatie de indiferenta: A=B.
Mai este de precizat ca, in abordarea ordinala a utilitatii si a echilibrului consumatorului, teoreticienii neoclasici au luat ca obiect al cercetarii stiintifice nu individul real, ci un model abstract al consumatorului rational, perfect informat, care urmareste maximizarea utilitatii ghidandu‑se dupa axiomele prezentate mai sus.
Instrumentul de baza folosit in teoria ordinala a utilitatii este curba de indiferenta, numita si curba de izoutilitate, introdusa pentru prima data de italianul Vilfredo Pareto (1848‑1923) si dezvoltata apoi de J.R. Hicks, G. Debreu, M. Allais etc.2.
2. Definitia si proprietatile curbei de indiferenta
Pentru simplificarea si asigurarea posibilitatii exprimarii grafice, sa presupunem ca un individ consumator are la dispozitie numai doua bunuri, X si Y, cu care poate efectua o infinitate de combinatii (altfel spus, din care poate constitui o infinitate de 'cosuri' sau 'panere' de consum). Acestea pot fi grupate in doua categorii:
combinatii care asigura acelasi nivel de satisfactie sau de utilitate;
combinatii care asigura niveluri diferite de satisfactie sau de utilitate.
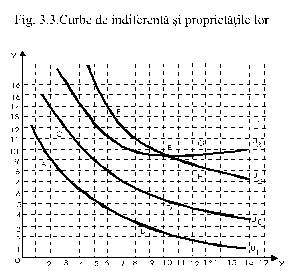
Multimea combinatiilor a doua bunuri, X si Y, care asigura consumatorului un nivel de utilitate identic se numeste curba de indiferenta.
Pe figura de mai sus sunt
reprezentate trei curbe de indiferenta, Uo, U1 si U2,
care indica trei niveluri diferite de utilitate. Daca ne situam pe curba Uo,
consumatorul va obtine aceeasi satisfactie sau utilitate, Uo,
consumand fie 'cosul' C, constituit din combinatia a 3 unitati din
bunul X si 12 unitati din bunul Y, fie 'cosul' D, constituit din 11
unitati din bunul X si 5 unitati din bunul Y, fie oricare alta combinatie
aferenta infinitatii punctelor de pe curba respectiva. 'Cosurile' sau
combinatiile situate pe curba de indiferenta U1, cum ar fi A (2
unitati din bunul X si 9 unitati din bunul Y) sau B (9 unitati din bunul X si 3
unitati din bunul Y) sau oricare alt punct de pe aceasta curba ofera un nivel
de satisfactie sau utilitate U1 mai redus decat Uo.
'Cosurile' de consum sau combinatiile situate pe curba de indiferenta
U2, cum ar fi E (6 unitati din bunul X si 13 unitati din bunul Y)
sau F (9 unitati din bunul X si 10 unitati din bunul Y) sau oricare alt punct
de pe aceasta curba ofera un nivel de utilitate U2, superior lui U0.
Putem formaliza cele de mai sus astfel: ![]()
![]()
![]() ,
in care U0, U1 si U2 sunt constante, iar
,
in care U0, U1 si U2 sunt constante, iar ![]() .
.
Deci, A=B; C=D; E=F, intrucat cuplurile (A, B), (C, D) si (E, F) se afla pe cate o curba de indiferenta, iar A<C; C<E, de unde rezulta A<E (relatia de tranzitivitate). Toate punctele situate la dreapta celor de pe curba U0 reprezinta combinatii ale bunurilor X si Y care ofera mai multa utilitate, iar toate punctele situate la stanga celor de pe curba de indiferenta U0 reprezinta combinatii care asigura mai putina utilitate.
Pentru un acelasi individ pot exista o infinitate de curbe de indiferenta, fiecare corespunzand unui nivel de satisfactie diferit. Ansamblul acestor curbe de indiferenta este denumit harta de indiferenta. Exista tot atatea 'harti de indiferenta' ca si numarul indivizilor.
Intersectia a doua curbe de indiferenta este imposibila. Aceasta se poate demonstra pe figura prin metoda reducerii la absurd: daca intersectia curbelor U2 si U3 ar fi posibila, atunci combinatiile exprimate pe punctele G si H ar trebui, din definitia curbelor de indiferenta, sa asigure acelasi nivel de utilitate ca si combinatia F. Or aceasta este imposibil deoarece G>H.
Curbele de indiferenta sunt descrescatoare. Aceasta proprietate deriva din ipoteza de rationalitate a consumatorului, potrivit careia individul nu‑si va continua niciodata consumul unui bun dincolo de punctul de satietate, cand utilitatea marginala a bunului respectiv devine negativa. Daca UmY ar fi negativa, o diminuare a cantitatii din bunul Y ar creste satisfactia individului (fiindca i‑ar reduce insatisfactia sau neplacerea provocata de consumul acestui bun), iar atunci, pentru a mentine utilitatea neschimbata, pentru a ne situa pe aceeasi curba de indiferenta, ar trebui sa se reduca si consumul lui X. Cantitatea din bunul Y si cea din bunul X ar varia in acelasi sens. Curba de indiferenta ar fi crescatoare. Insa, cum utilitatea marginala este mereu pozitiva, diminuarea cantitatii din bunul Y reduce utilitatea totala a individului. Mentinerea neschimbata a utilitatii totale, pentru a ne situa in continuare pe aceeasi curba de indiferenta, nu poate fi realizata decat prin cresterea cantitatii consumate din celalalt bun, X. Deci, de‑a lungul curbei de indiferenta, exista o relatie inversa, descrescanda sau negativa intre cantitatea din bunul X si cantitatea din bunul Y: daca X creste, Y scade si invers. Acest fapt se poate observa pe figura 3: Pornind de la combinatia A (2 unitati din bunul X si 9 unitati din bunul Y), daca reducem numarul unitatilor bunului Y la 3, pentru a mentine neschimbata utilitatea U1 trebuie sa crestem numarul unitatilor bunului X de la 2 la 9 (punctul B).
Deci forma descrescatoare a curbei de indiferenta rezulta din faptul ca UmX si UmY sunt presupuse pozitive, ca urmare a rationalitatii comportamentului consumatorului.
Curbele de indiferenta sunt convexe. Relatia descrescatoare intre cantitatea din bunul X si cantitatea din bunul Y am fi avut‑o si de‑a lungul unei drepte, asa cum rezulta din figura 4. Curbele de indiferenta sunt insa convexe, adica, in termeni nematematici, ele nu sunt drepte, ci curbate spre punctul de origine al axelor de coordonate, spre partea de jos: inclinatia lor se diminueaza in mod progresiv de la stanga la dreapta.
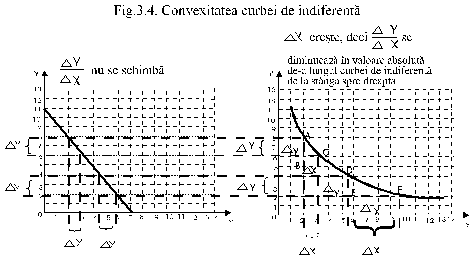
Dupa cum se poate observa din figura 4., daca functia de utilitate ar fi liniara, exprimata printr‑o dreapta, de‑a lungul acesteia, o diminuare a cantitatii bunului Y, cu o marime data, Y, presupune, pentru a mentine utilitatea neschimbata, o crestere a cantitatii din bunul X, cu o marime X, care ramane neschimbata pe orice portiune a dreptei ne‑am situa. Aceasta s‑ar intampla insa numai daca bunurile X si Y ar fi perfect substituibile, ceea ce ar insemna ca individul, considerandu‑le perfect identice, sa fie indiferent fata de ponderea fiecarui bun in 'cosul' sau format din cele doua bunuri. L‑ar interesa numai cantitatea totala din bunurile X si Y, o unitate din bunul X fiind mereu echivalenta cu o unitate din bunul Y.
Analiza economica se intereseaza insa in mod normal de alegerea intre doua bunuri imperfect substituibile.
De aceea, dimpotriva, de‑a lungul curbei de indiferenta, o aceeasi diminuare a cantitatii lui Y nu poate fi compensata decat printr‑o cantitate crescanda din bunul X. Cum explicam acest fapt? De unde provine? Sa ne reamintim de principiul utilitatii marginale descrescande la cresterea cantitatii consumate. Cand se diminueaza cu o anumita cantitate volumul consumat din bunul Y, substituita cu o alta cantitate din bunul X, primul bun devine din ce in ce mai rar, astfel incat utilitatea sa marginala (UmY) creste, devine din ce in ce mai mare. Ca urmare, utilitatea totala se diminueaza din ce in ce mai repede si doar o cantitate crescanda din celalalt bun, X, va putea mentine utilitatea totala neschimbata. Cu atat mai mult cu cat si bunul X, fiind din ce in ce mai abundent, utilitatea sa marginala se diminueaza.
Rata marginala de substituire (RMS)
S‑a vazut ca forma curbei de indiferenta este determinata de ritmul in care bunul Y este substituit de bunul X de‑a lungul acestei curbe. Cu cat bunul Y este substituit intr‑un ritm mai rapid de catre bunul X, cu atat panta curbei de‑a lungul careia se face aceasta substituire este mai puternica. Pentru a intelege mai usor acest fapt, presupunem doua functii liniare de utilitate, U1 si U2, reprezentate grafic prin dreptele D1 si D2, cu inclinatii sau pante diferite. Se observa din figura 5. ca atunci cand cantitatea din bunul X creste cu X, Y se diminueaza foarte rapid de‑a lungul dreptei D1 si mult mai lent de‑a lungul dreptei D2. Ritmul sau 'viteza' cu care Y variaza ca reactie la variatia lui X se masoara deci prin panta dreptei de indiferenta, care se determina ca raport intre variatia lui Y, Y, si variatia lui X, X, intre doua puncte oarecare.

Deci, panta dreptei =![]() (6.)
(6.)
In timp ce, in cazul unei drepte, raportul Y/X este identic in toate punctele sale, de‑a lungul unei curbe convexe, asa cum rezulta si din figura 4., valoarea absoluta a pantei se diminueaza de la stanga spre dreapta, ea variind in fiecare punct. De aceea, singura modalitate de determinare a ritmului de variatie a cantitatii din bunul Y ca reactie la modificarea cantitatii din bunul X este calculul derivatei lui Y in raport cu X, care reprezinta 'panta intr‑un punct' a curbei sau, intr‑o exprimare matematica, 'panta dreptei tangente la curba in acel punct'. Ea masoara variatia lui Y pentru o variatie infinit de mica a lui X(X
Cu aceste precizari facute, putem spune ca rata marginala de substituire (R.M.S.) intre doua bunuri, Y si X, masoara variatia cantitatii necesare a fi consumate din bunul Y, de‑a lungul unei curbe de indiferenta, pentru a compensa o variatie infinit de mica (infinitezimala) a cantitatii consumate din bunul X, astfel incat nivelul utilitatii totale sa ramana neschimbat.
Cum RMS nu este altceva decat 'panta intr‑un punct' a curbei, ea variaza in fiecare punct si este continuu descrescanda de‑a lungul curbei. RMS este determinata prin derivata lui Y in raport cu X, fiind negativa deoarece variatiile celor doua cantitati sunt de sensuri contrarii. Pentru a fi exprimata insa in valori pozitive, RMS se defineste cu un semn '-' plasat in fata intre paranteze rotunde, pentru a‑i sublinia caracterul conventional:
![]() (4.7.)
(4.7.)
De exemplu, sa presupunem ca pentru o persoana, intr‑o zi caniculara de vara, utilitatea asigurata de consumul a doua bunuri ‑ bautura racoritoare (X) masurata cu paharul si pateuri (Y) avand ca unitate de masura 'bucata' ‑ este definita de functia :
![]() (4.8)
(4.8)
Cand
consumatorul doreste sa‑si mentina neschimbata utilitatea, la un nivel pe
care el il apreciaza, sa zicem, la 10, substituind bauturii racoritoare
pateurile, curba de indiferenta va fi cea reprezentata in fig. 4.6., care este
o hiperbola echilaterala. Din U(X,U)=XY=10, rezulta ![]() ,
iar
,
iar ![]() ,
adica
,
adica ![]() .
RMS variaza in fiecare punct al curbei de indiferenta.
.
RMS variaza in fiecare punct al curbei de indiferenta.
In punctul A, de coordonate 1si 10, deci care reprezinta o combinatie sau un 'cos' de consum format dintr‑un pahar de bautura racoritoare si 10 bucati de pateuri, RMS este 10. Aceasta inseamna ca, in punctul A, o crestere cu un pahar a consumului de bautura racoritoare necesita o diminuare cu 10 bucati a cantitatii consumate din pateuri, daca se vrea mentinerea neschimbata a utilitatii totale. RMS se diminueaza tot mai mult pe masura ce ne deplasam spre dreapta pe curba de indiferenta, astfel incat in punctul D(10,1) ajunge la 0,1, cand de fapt persoana aproape nu vrea sa mai substituie cele doua bunuri.
|
|
|
Se observa, si din acest exemplu, ca RMS se poate calcula intr‑un punct oarecare al curbei de indiferenta, dar nu intre doua puncte.
Intre doua puncte se poate
calcula o rata medie de substituire (![]() ).
Daca ne vom folosi de exemplul de mai sus si vom calcula
).
Daca ne vom folosi de exemplul de mai sus si vom calcula ![]() intre punctele A si C, vom avea:
intre punctele A si C, vom avea:
![]() (9)
(9)
Aceasta rata ne arata cat trebuie sacrificat din Y pentru cresterea cu o unitate a lui X, cand se trece de la combinatia A la combinatia C. In acest caz, cresterea cantitatii consumate din bautura racoritoare, (bunul X) cu 4 pahare, necesita, pentru mentinerea neschimbata a utilitatii (adica pentru a ne situa pe curba de indiferenta), o diminuare a consumului de pateuri (bunul Y) cu 8 bucati (o variatie in sens invers, de 2 ori mai mare).
RMS si ![]() nu pot fi identice decat daca panta intre doua
puncte si panta intr‑un punct ar fi egale pe oricare portiune a curbei de
indiferenta, ceea ce nu se poate intampla decat daca curba de indiferenta ar fi
o dreapta.
nu pot fi identice decat daca panta intre doua
puncte si panta intr‑un punct ar fi egale pe oricare portiune a curbei de
indiferenta, ceea ce nu se poate intampla decat daca curba de indiferenta ar fi
o dreapta.
4. Exemple de functii de utilitate si de curbe de indiferenta
care le corespund
Este dificil de determinat functiile de utilitate implicate de modul de ordonare si alegere a combinatiilor de consum efectuate de catre indivizi.
Ne putem da seama de formele lor observand comportamentul consumatorului ca reactie a acestuia la schimbarile survenite in venit, preturi si alti factori. De aceea este necesar sa examinam cateva forme particulare pe care le pot lua functiile de utilitate pentru doua bunuri. Hartile de indiferenta cu aceste curbe sunt ilustrate in fig. 7.
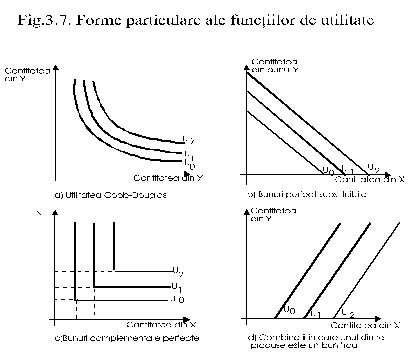
Graficul a)reprezinta forma familiara a curbei de indiferenta cu care deja ne‑am intalnit. Functia de utilitate care genereaza asemenea curbe are forma:
![]() (10)
(10)
unde si sunt constante pozitive.
In exemplul pe care l‑am luat cu bautura racoritoare si pateurile, am studiat un caz particular al acestei functii, in care =1. Forma mai generala prezentata in ecuatia 10 este denumita de obicei functia de utilitate Cobb‑Douglas, dupa numele a doi cercetatori care au folosit‑o in studiile lor cu privire la functiile de productie din economia Statelor Unite.
Curbele de indiferenta sub forma liniilor drepte din fig. 7.b), sunt generate de o functie de utilitate descrisa de ecuatia:
![]() (11)
(11)
unde de asemenea si sunt constant pozitive. Dupa cum am amintit deja, aceasta forma a curbelor de indiferenta este specifica combinatiilor a doua bunuri, X si Y, perfect substituibile, de obicei bunuri care, in esenta, sunt acelasi produs, pentru care RMS ramane constanta, indiferent de ponderea pe care o are in 'cosul' de consum Y sau X.
O situatie opusa cazului preferintelor pentru bunuri perfect substituibile este cea ilustrata de fig. 7.c), unde curbele de indiferenta au forma literei 'L', fiind aplicabile alegerilor pentru bunuri perfect complementare, care nu pot fi consumate decat impreuna, de exemplu cafeaua si zaharul. Forma acestor curbe de indiferenta evidentiaza faptul ca perechile respective de bunuri vor fi consumate intr‑o proportie fixa, exprimata de dimensiunea pe verticala. De exemplu, o persoana care prefera 5 grame de zahar la 10 grame de cafea, va consuma 10 grame de zahar la 20 grame cafea si 15 grame de zahar la 30 grame cafea cand doreste sa‑si mareasca utilitatea de la Uo la U1 si apoi la U2. O cantitate suplimentara de cafea, fara a spori si zaharul nu va determina cresterea utilitatii, cum nici o cantitate suplimentara de zahar, fara cresterea cantitatii de cafea nu va duce la sporirea satisfactiei individului. Numai consumand cafeaua si zaharul impreuna se poate asigura cresterea utilitatii.
Ecuatia matematica a functiei de utilitate care genereaza aceste curbe de indiferenta in forma de 'L' este:
![]() (12)
(12)
unde si sunt constante pozitive, iar operatorul 'min.' inseamna ca utilitatea este data de cel mai mic dintre cei doi termeni din paranteza.
In exemplul cu cafeaua si zaharul, daca notam cu X cantitatea de cafea (10 g.) si cu Y cantitatea de zahar (5 g.) pentru o ceasca, utilitatea va fi data de ecuatia:
![]() (1)
(1)
fiind
egala cu 10 deoarece ![]() .
20 grame de cafea si 5 grame de zahar vor asigura aceeasi utilitate, deoarece
min. (20,10)=10, adica o cantitate suplimentara de cafea, neinsotita insa de
cresterea zaharului, nu ofera individului nici o satisfactie suplimentara.
Pentru ca utilitatea sa creasca, la dublarea cantitatii de cafea trebuie sa se
asigure dublarea cantitatii de zahar si atunci, U=min. (20,20)=20, nivelul
utilitatii fiind exprimat pe fig. 7.c) de curba 'L' U1.
Deci, oricat de mult ar spori cantitatea de cafea, adica variabila X, daca
zaharul ramane la cantitatea Y0, nivelul utilitatii se mentine la U0,
ca si atunci cand ar spori cantitatea de zahar (variabila Y), dar cafeaua ar
ramane la cantitatea X0. Daca se doreste majorarea utilitatii de la
nivelul U0 la U1, trebuie sa creasca si cafeaua (cel
putin la cantitatea X1) si zaharul (cel putin la cantitatea Y1).
.
20 grame de cafea si 5 grame de zahar vor asigura aceeasi utilitate, deoarece
min. (20,10)=10, adica o cantitate suplimentara de cafea, neinsotita insa de
cresterea zaharului, nu ofera individului nici o satisfactie suplimentara.
Pentru ca utilitatea sa creasca, la dublarea cantitatii de cafea trebuie sa se
asigure dublarea cantitatii de zahar si atunci, U=min. (20,20)=20, nivelul
utilitatii fiind exprimat pe fig. 7.c) de curba 'L' U1.
Deci, oricat de mult ar spori cantitatea de cafea, adica variabila X, daca
zaharul ramane la cantitatea Y0, nivelul utilitatii se mentine la U0,
ca si atunci cand ar spori cantitatea de zahar (variabila Y), dar cafeaua ar
ramane la cantitatea X0. Daca se doreste majorarea utilitatii de la
nivelul U0 la U1, trebuie sa creasca si cafeaua (cel
putin la cantitatea X1) si zaharul (cel putin la cantitatea Y1).
Pentru ca nici unul din cele doua bunuri X si Y din ecuatia 12. sa nu fie in exces, mai trebuie pusa conditia:
![]() (14)
(14)
de unde rezulta:
![]() (15)
(15)
relatie
care indica proportia fixa dintre cantitatile celor doua bunuri necesare pentru
a mentine utilitatea reflectata de o anume curba de indiferenta. In exemplul
nostru ilustrat de ecuatia 1, pentru a creste utilitatea de la U0 la
U1, la U2 s.a.m.d., fara ca zaharul sau cafeaua sa fie in
exces, este necesar ca intre bunul Y (zaharul) si bunul X (cafeaua) sa se
mentina mereu proportia de ![]() .
.
In fine, curbele de indiferenta din fig. 7.d), sub forma dreptelor cu panta pozitiva, sunt aplicabile situatiilor in care unul dintre cele doua bunuri, X si Y, de exemplu Y, ar fi un bun 'rau', care provoaca disconfort, adica reduce utilitatea. Ne putem imagina o combinatie de acest tip considerand bunul X splendorile oferite de cadrul natural al Deltei Dunarii, iar bunul Y contactul neplacut, chiar periculos cu tantarii din aceste locuri. Consumatorul, in cazul nostru turistul, nu va accepta sa patrunda mai profund in delta, unde se va confrunta cu mai multi tantari (in termenii teoriei alegerii, va fi nevoit sa 'consume' mai multe intepaturi oferite de aceste insecte oribile) decat daca produsul turistic ce i se ofera se va mari (privelisti mai salbatice, specii de plante, animale sau pasari mai rare, o bucatarie traditionala mai inedita etc.). Deci, odata cu cresterea cantitatii din bunul 'rau' ‑ contactul cu tantarii ‑ care provoaca dezutilitate, diminueaza utilitatea, trebuie sa creasca si cantitatea din bunul 'bun' ‑ produsul turistic ‑ care sporeste utilitatea, astfel incat nivelul utilitatii totale sa se mentina neschimbat.
Functia matematica ce poate defini harta de indiferenta din fig. 7.d) este:
![]() (16.)
(16.)
unde > 0, iar < 0. Deci cresterile din X vor determina sporirea utilitatii in timp ce cresterile din Y o vor diminua, astfel incat, pentru mentinerea neschimbata a ei, este necesara modificarea concomitenta a cantitatilor celor 2 bunuri, dar in sens contrar.
5. Echilibrul consumatorului
Am vazut ca prin curba de indiferenta se formalizeaza preferintele subiective ale consumatorilor, indicandu‑ni‑se doar modul in care indivizii sunt dispusi sa substituie diferitele bunuri intre ele. Ele ne mai sugereaza si faptul ca obiectivul consumatorului consta in atingerea curbei de indiferenta cea mai ridicata posibil, care exprima cel mai ridicat nivel al utilitatii ce se poate obtine din combinatia sau alegerea respectiva. Acestea nu reprezinta decat o parte a problemei: ceea ce este dorit. Insa, o teorie completa a consumatorului trebuie sa mai permita si confruntarea dezirabilului cu posibilul. Pentru a alege, consumatorul nu ia in considerare numai preferintele sau dorintele sale. El este obligat sa tina seama si de posibilitatile sale de a procura bunurile respective, posibilitati care sunt limitate.
5.1. Constrangerea bugetara
Aceste posibilitati sunt legate de venitul disponibil al consumatorului (V) si de preturile celor doua bunuri (Px si Py). Toate aceste trei variabile sunt independente de deciziile de consum pe care le ia individul, Astfel, venitul depinde in esenta de pretul muncii individului, adica de salariu, care este o marime ce se formeaza pe piata muncii. Preturile Px si Py rezulta din confruntarea cererii si ofertei pe piata celor doua bunuri. Deci V, Px si Py sunt variabile exogene, care se impun individului in momentul alegerii, sub forma unor constrangeri sau restrictii exogene.
Limita impusa alegerii consumatorului de dimensiunea venitului sau si de nivelul preturilor reprezinta constrangerea bugetara. Ea consta in faptul ca cheltuielile de consum pe care le efectueaza un individ nu pot depasi venitul sau, adica Venitul = cheltuiala pentru procurarea bunului X + cheltuiala pentru procurarea bunului Y. Or, cheltuiala pentru procurarea unui bun este, in esenta, cantitatea din acel bun inmultita cu pretul lui. si atunci, folosind notatiile carora le‑am prezentat semnificatiile mai sus, putem scrie:
![]() (17)
(17)
ceea ce se poate reprezenta si grafic, printr‑o dreapta care exprima multimea combinatiilor (X, Y) ce pot fi procurate de un consumator tinand seama de venitul sau si preturile bunurilor X si Y.
Pentru a trasa o dreapta este
suficient sa cunoastem doua puncte ale sale. Dupa cum observam din fig. 7.,
acestea sunt reprezentate de intersectiile dreptei cu axele de coordonate: pe
axa ordonatei intersectia exprima cantitatea maxima ce poate fi consumata din
bunul Y daca intreg venitul V este alocat procurarii acestui bun, adica daca s‑ar
consuma zero din bunul X: ![]() ,
ceea ce inseamna
,
ceea ce inseamna ![]() ;
pe axa abscisei intersectia exprima cantitatea maxima ce poate fi consumata din
bunul X daca intregul venit V este alocat procurarii acestui produs, adica daca
s‑ar consuma zero din bunul Y:
;
pe axa abscisei intersectia exprima cantitatea maxima ce poate fi consumata din
bunul X daca intregul venit V este alocat procurarii acestui produs, adica daca
s‑ar consuma zero din bunul Y: ![]() ,
de unde rezulta
,
de unde rezulta ![]() ;
;
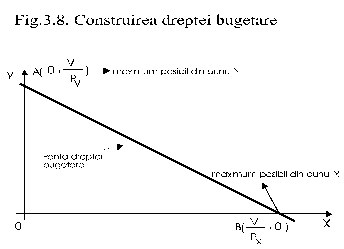
Deci,
coordonatele punctelor de intersectie sunt ![]() si
si ![]() .
Panta dreptei bugetare, in marime absoluta, este de fapt tangenta unghiului ABO
din triunghiul dreptunghic AOB:
.
Panta dreptei bugetare, in marime absoluta, este de fapt tangenta unghiului ABO
din triunghiul dreptunghic AOB:
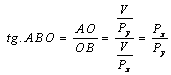
Ecuatia constrangerii bugetare
poate fi rescrisa sub forma ecuatiei unei drepte de tipul y = ax + b, unde 'a' reprezinta panta. Astfel, ![]() este echivalenta cu
este echivalenta cu ![]() si impartind prin Py:
si impartind prin Py:
![]() (18.)
(18.)
Deci,
panta dreptei bugetare este ![]() ;
;
Aceasta ecuatie descrie modul
cum evolueaza consumul lui Y in functie de cel al lui X. Daca X=0, consumul lui
Y este la maximul sau ![]() ;
daca X>0, consumul lui Y devine
;
daca X>0, consumul lui Y devine ![]() minus
ceva, cat s‑a cheltuit pentru X. Acest ceva va fi cu atat mai mare cu cat
Px va fi mai mare. De aici, rezulta ca ritmul in care Y se
diminueaza cand X creste(nimic altceva decat panta dreptei bugetare) depinde de
pretul relativ al celor doua bunuri. Daca Px > Py, Y
se va diminua mai repede. Daca Px < Py, Y se va
diminua mai lent. In primul caz, panta este mai mare, iar in al doilea panta
este mai usoara. Daca Px ar fi zero, adica daca bunul X ar fi
gratuit, cantitatea din bunul Y nu s‑ar mai diminua, panta ar fi zero,
iar dreapta bugetara ar fi orizontala.
minus
ceva, cat s‑a cheltuit pentru X. Acest ceva va fi cu atat mai mare cu cat
Px va fi mai mare. De aici, rezulta ca ritmul in care Y se
diminueaza cand X creste(nimic altceva decat panta dreptei bugetare) depinde de
pretul relativ al celor doua bunuri. Daca Px > Py, Y
se va diminua mai repede. Daca Px < Py, Y se va
diminua mai lent. In primul caz, panta este mai mare, iar in al doilea panta
este mai usoara. Daca Px ar fi zero, adica daca bunul X ar fi
gratuit, cantitatea din bunul Y nu s‑ar mai diminua, panta ar fi zero,
iar dreapta bugetara ar fi orizontala.
Deci panta ![]() .
.
5.2. Combinatia optimala
Cautand satisfactia maxima pe care o poate oferi consumul unei combinatii de doua bunuri cumparate dintr‑un venit limitat, individul va trebui sa atinga curba de indiferenta cea mai ridicata posibil, dar astfel incat combinatia aleasa sa fie plasata pe dreapta sa bugetara. Aceasta inseamna ca el va retine punctul de pe aceasta dreapta care atinge curba cea mai ridicata. Astfel spus, combinatia optimala este definita de punctul in care curba de indiferenta este tangenta la dreapta bugetara (punctul E din fig. 9.).
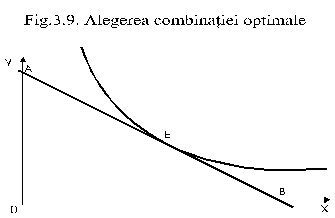
Aceasta inseamna ca in punctul E panta curbei de indiferenta (dY/dX) si cea a dreptei bugetare (- Px/Py) sunt confundate. Deci:
![]() (19)
(19)
Dar, prin definitie:
![]() (3,20)
(3,20)
Din relatiile (19) si (20) rezulta:
![]() (21)
(21)
Deci:
![]() (22)
(22)
Pe de alta parte insa, daca exprimam matematic variatia utilitatii totale legata de variatiile cantitatilor din bunurile X si Y, avem:
![]() (23)
(23)
Daca ne situam pe o curba de indiferenta, utilitatea totala este aceeasi in oricare punct, astfel incat dU = 0. Atunci relatia (23) devine:
![]() (24)
(24)
de unde:
![]()
![]() (25)
(25)
Cum ![]() ,
rezulta ca
,
rezulta ca ![]() , (26)
, (26)
Deci, RMS se poate exprima si prin raportul dintre utilitatile marginale ale celor doua bunuri.
Se poate arata acum ca determinarea combinatiei optimale a consumatorului, din punctul de vedere al abordarii ordinale, este compatibila cu rezultatul obtinut in cadrul abordarii cardinale. Intr‑adevar, din relatiile (26) si (22) rezulta:
![]() (27)
(27)
ceea ce este echivalent cu:
![]() (28)
(28)
relatie identica cu conditia de echilibru a consumatorului in abordarea cardinala a utilitatii in cadrul economiei monetare (relatia 5. de la subcapitolul 2.).
Sa intelegem acum mai bine modul de determinare a echilibrului consumatorului printr‑un exemplu: sa presupunem ca utilitatea cautata de un individ prin consumul a doua bunuri, X si Y, este data de functia U=U(X,Y)=X(Y-2), unde X si Y sunt cantitatile din bunurile respective, in conditiile in care venitul de care dispune (V) este de 50 unitati monetare iar preturile celor doua produse sunt Px = 10 u.m. iar Py = 5 u.m.
Pentru a determina combinatia optimala sau echilibrul consumatorului, adica utilitatea maxima permisa de constrangerea bugetara, folosim relatia 27 sau 28:
![]() , de exemplu.
, de exemplu.
![]()
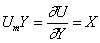
deci: ![]() sau 5(Y-2)=10X, ceea ce este echivalent cu:
sau 5(Y-2)=10X, ceea ce este echivalent cu:
10X - 5Y + 10 = 0 (29)
Impreuna cu ecuatia constrangerii bugetare: 50 = 10X + 5Y, ceea ce este echivalent cu :
10X + 5Y - 50 = 0 (30)
se formeaza un sistem de 2 ecuatii cu doua necunoscute, X si Y:
![]()
Punctul E1 de coordonate (2, 6) din fig. 10. indica combinatia optima (2 unitati din bunul X si 6 unitati din bunul Y) sau punctul de echilibru al consumatorului, intrucat, cu venitul sau de 50 u.m. el atinge curba de indiferenta cea mai ridicata posibil, care‑i asigura o utilitate de: U=X(Y-2)=2(6-2)=8. Deci, curba de indiferenta U1 din fig. 10 este definita de functia:
U=U(X,Y)=X(Y-2)=8, sau
![]() (31)
(31)
Triunghiul hasurat cuprinde toate posibilele combinatii pe care le poate alege consumatorul in limita venitului sau de 50 u.m., deci cele care indeplinesc conditia:
![]() (32)
(32)
Dar, toate aceste combinatii reprezinta o alocare a venitului de 50 u.m. neoptimala, in afara alegerii din punctul E1, care se situeaza pe curba de indiferenta U1. Toate celelalte alegeri cuprinse in triunghiul hasurat, chiar situate pe dreapta bugetara (combinatii realizate prin cheltuirea integrala a venitului) s‑ar plasa pe curbe de indiferenta aflate la stanga lui U1, deci s‑ar asigura un nivel de utilitate mai redus, cum usor se poate intui din fig. 10.
|
|
|
5. Efectul variatiilor de pret
Ce se intampla atunci cand se modifica preturile celor doua bunuri sau doar al unuia dintre ele? Altfel exprimat, cand se modifica pretul relativ, adica pretul unui bun exprimat prin pretul celuilalt. Pe de o parte, se modifica panta dreptei bugetare (am vazut ca aceasta este egala tocmai cu raportul dintre Px si Py). Pe de alta parte, se modifica si puterea de cumparare a venitului nominal ramas nemodificat, adica numarul de bucati ce pot fi cumparate cu o marime data a venitului nominal, care se mai numeste si venit real. Aceasta va creste si deci va asigura o ridicare a nivelului de utilitate, daca pretul va scadea, sau se va diminua, reducand nivelul de utilitate, daca pretul se va majora.
Daca in exemplul anterior am presupune ca Px se reduce de la 10 u.m. la 4 u.m., Py ramanand nemodificat, cu acelasi venit, de 50 u.m., se va putea procura o cantitate maxima de 50:4=12,5 unitati din bunul X in loc de 5, astfel incat dreapta bugetara, mentinandu‑si neschimbat punctul de intersectie cu ordonata, isi va deplasa extremitatea de pe abscisa de la punctul B(5;0) la C(12,5;0). Desigur, se va modifica si ecuatia dreptei bugetare, care devine:
![]() (33),
(33),
si ecuatia functiei de utilitate si, o data cu acestea, pozitia punctului de echilibru al consumatorului. Printr‑un calcul similar celui prin care am determinat coordonatele punctului E1 din fig. 10 aflam noul punct de echilibru al consumatorului, E2, de coordonate (5;6). Noul nivel al utilitatii maxime obtinute prin cresterea cantitatii consumate din bunul X, ca urmare a reducerii pretului sau, este de:
![]()
Ecuatia noii curbe de indiferenta va fi:
![]() (34)
(34)
Daca pretul bunului X se va mai reduce odata, ajungand la 2 u.m., cantitatea maxima ce va putea fi consumata din X creste la 25 unitati (venitul si Py raman neschimbate). Ecuatia noii drepte bugetare va fi:
![]() (35)
(35)
Coordonatele noului punct de echilibru vor fi (10;6), iar ecuatia curbei de indiferenta, cu un nivel de utilitate de aceasta data de 40, va fi:
![]() (36)
(36)
Se observa deci ca reducerea pretului unuia dintre bunuri, in conditiile mentinerii constante a pretului celuilalt bun si a venitului, are ca efect, pe de o parte, cresterea puterii de cumparare sau a nivelului venitului real, care va permite plasarea consumatorului pe o curba de indiferenta situata mai la dreapta, deci obtinerea unui nivel de utilitate mai ridicat, iar pe de alta parte, diminuarea pantei dreptei bugetare sau ratei marginale de substituire. Diminuarea pantei (in cazul reducerii lui Px) sau cresterea ei (in cazul majorarii lui Px) are loc prin rotirea dreptei bugetare in jurul punctului A (din fig. 10), care ramane fix, ca urmare a faptului ca pretul Py si venitul nu se modifica.
Daca se modifica ambele preturi, venitul mentinandu‑se constant, pot apare urmatoarele situatii: a) Px si Py se modifica in aceeasi proportie, de exemplu n, si in acelasi sens, panta dreptei bugetare ramane neschimbata:
![]()
Apar insa si aici doua cazuri:
a1) daca n>1, adica daca preturile cresc in aceeasi proportie, n, cu venitul V, neschimbat, individul isi va putea procura o cantitate maxima din bunul X sau din bunul Y de n ori mai mica, ceea ce, grafic, se va reprezenta printr‑o deplasare a dreptei bugetare, paralela cu ea insasi, spre originea axelor de coordonate (vezi, fig. 11). Desigur, mai este necesara conditia, atunci cand bunurile X si Y sunt imperfecte divizibile, ca
max.(nPx, nPy) V (37)
Altfel, nu ar mai putea fi procurata cu venitul V nici o unitate din cele doua bunuri. Asa cum se observa din figura 11.a), noii pozitii a dreptei bugetare, d1, ii corespunde curba de indiferenta U1, care, evident, reprezinta un nivel mai scazut de utilitate sau ‑ cum se mai poate spune ‑ un standard de viata mai redus.
a2) daca, dimpotriva n<1, adica daca preturile scad in aceeasi proportie, fara a se modifica venitul nominal, dreapta bugetara se va deplasa tot paralel cu ea insasi, dar in directie opusa originii axelor de coordonate (in pozitia d2 din fig. 11.a), careia ii va corespunde curba de indiferenta U2).
b) Px si Py se maresc, ambele, dar nu in aceeasi proportie, ci Px de n ori, iar Py de m ori. si aici sunt doua cazuri:
b1) daca Px se mareste intr‑o proportie mai mare decat Py (deci n>m), cantitatea maxima ce poate fi procurata din X cu venitul V ramas constant se micsoreaza mai mult decat cantitatea maxima din Y, astfel incat dreapta bugetara se deplaseaza in pozitia d1, din fig. 11.b), marindu‑si panta.
b2) daca, dimpotriva, Px se mareste intr‑o proportie mai mica decat Py (deci n<m), dreapta bugetara se va deplasa in pozitia d2, diminuandu‑si panta (vezi fig. 11.b). Se observa, din reprezentarea grafica, faptul ca in ambele cazuri, b1 si b2, nivelul utilitatii exprimat de curbele de indiferenta U1 si U2 este inferior situatiei initiale.
c) Px si Py se micsoreaza ambele, dar, de asemenea, nu in aceeasi proportie, ci Px de n ori, iar Py de m ori, nm. Aceleasi doua situatii:
c1) daca Px se micsoreaza intr‑o proportie mai mare decat Py (deci daca n>m), cantitatea maxima ce poate fi procurata din bunul X cu venitul constant V creste si ea intr‑o proportie mai mare decat cea din bunul Y. Dreapta bugetara se deplaseaza din pozitia d0 in pozitia d1 diminuandu‑si panta (vezi, fig. 11.c).
c2) daca, dimpotriva, Px se micsoreaza intr‑o proportie mai mica decat Py (deci daca n<m), dreapta bugetara se deplaseaza din pozitia d0 in pozitia d2.
Se observa, din reprezentarea grafica (fig. 11.c) faptul ca, in ambele cazuri, curbele de indiferenta corespunzatoare noilor pozitii ale dreptei bugetare, U1 si U2, sunt la dreapta curbei initiale U0, deci exprima un nivel mai ridicat de utilitate.
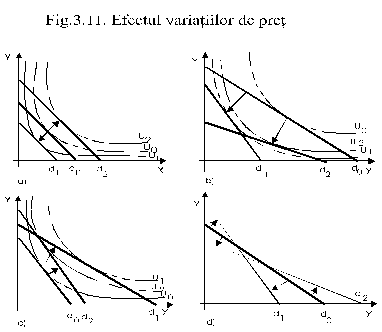
d) Px si Py variaza in proportii si sensuri diferite. Fara a mai aprofunda analiza, sa retinem si aici doua cazuri:
d1) daca Px se mareste de n ori, iar Py se micsoreaza de m ori, dreapta bugetara sufera un proces de rasucire, ajungand in pozitia d1 din fig. 11.d), marindu‑si panta.
d2) daca Px se micsoreaza de n ori in timp ce Py se mareste de m ori, fara ca venitul nominal sa se modifice, ne dam seama, printr‑un rationament similar celor de mai sus ca dreapta bugetara se deplaseaza in pozitia d2, diminuandu‑si panta.
5.4. Efectul variatiilor de venit
Cand se modifica doar venitul nominal, preturile celor doua bunuri ramanand neschimbate, situatia este asemanatoare cu cea descrisa la situatia a) de mai sus, cresterea sau diminuarea puterii de cumparare a consumatorului si deci a nivelului sau de satisfactie datorandu‑se de aceasta data cresterii sau diminuarii venitului si nu diminuarii sau cresterii preturilor celor doua bunuri in aceeasi proportie.
Deci, o crestere a venitului determina deplasarea dreptei bugetare si a curbei de indiferenta corespunzatoare spre dreapta , paralele cu ele insele, iar o diminuare a venitului determina deplasarea paralela spre stanga, asa cum arata reprezentarea grafica din fig. 11.a).
Desigur, realitatile pietei in care se misca si ia decizii consumatorul se pot infatisa si in numeroase alte situatii, rezultate din diversele combinatii ale cazurilor prezentate mai sus.
Studierea efectelor variatiilor preturilor si venitului asupra comportamentului consumatorului ne va permite o mai buna intelegere a continutului teoriei cererii la care trecem in tema urmatoare.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4694
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved