| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
METODA SIMPLEX PENTRU REZOLVAREA PROBLEMELOR DE PROGRAMARE LINIARA
1. Metoda simplex pentru probleme in forma standard. Studiu de caz
In capitolul 1, sectiunea 1.4 este prezentata o procedura de calcul a unei solutii optimale pe baza multimii punctelor extrem. Metoda simplex este o varianta mai eficienta de calcul a unei solutii optimale si este bazata, de asemenea, pe calculul solutiilor admisibile de baza.
Fie problema de programare liniara in forma standard,
(1)
![]()
cu restrictiile
(2)
![]()
(3)
![]()
unde A![]() este o matrice
este o matrice ![]() ,
, ![]() ,
, ![]() si
si ![]() . In continuare vom presupune
. In continuare vom presupune ![]() . Prin introducerea a m
variabile slack, notat
. Prin introducerea a m
variabile slack, notat![]() , este obtinuta forma canonica a problemei de
programare liniara definita prin (1), (2) si (3),
, este obtinuta forma canonica a problemei de
programare liniara definita prin (1), (2) si (3),
(4)
![]()
cu restrictiile
(5)
![]()
(6)
![]()
unde A este o matrice ![]()

![]() ,
, ![]() si
si ![]() .
.
Definitia 1. Fie S multimea solutiilor admisibile ale problemei de programare liniara definita de (1), (2) si (3).. Doua puncte extrem ale lui S sunt adiacente daca au in comun, ca solutii de baza si admisibile, una si numai una din variabilele de baza considerate.
Exemplul
Pentru prezentarea metodei simplex, vom considera in continuare urmatoarea problema de tip analiza activitatii de productie.
In procesul de prelucrare a butucilor, o fabrica de cherestea furnizeaza scandura de doua tipuri: finisata, notata cu Prod1, si pentru constructii, notata cu Prod Pentru obtinerea a 1000 de unitati de scandura finisata procedura de taiere dureaza 2 ore si procedura de rindeluire dureaza 5 ore. Pentru furnizarea a 1000 unitati de scandura de constructii, procesul de taiere dureaza 2 ore si cel de rindeluire necesita 3 ore. Fierastraul industrial cu care este realizata taierea poate fi folosit 8 ore pe zi si rindeaua este disponibila 15 ore pe zi.
Daca profitul obtinut din producerea a 1000 unitati de produs este de 120 lei in cazul scandurii finisate, respectiv 100 de lei in cazul scandurii de constructii, se cere sa se determine cantitatea de scandura din fiecare tip, in mii de unitati, care trebuie produsa zilnic pentru maximizarea profitului fabricii.
Modelul
matematic este urmatorul. Fie x
cantitatea din Prod1 si y cantitatea din Prod2 fabricate zilnic. Procesul de taiere necesita
zilnic ![]() ore, in timp ce rindeluirea dureaza
ore, in timp ce rindeluirea dureaza ![]() ore. Rezulta,
ore. Rezulta,
![]()
Evident,
![]() .
.
Profitul
este calculat prin ![]() .
.
Este obtinuta problema de programare liniara in forma standard,
Maximizeaza
![]()
cu restrictiile
![]()
![]()
In forma canonica, problema este formulata prin,
(7)
Maximizeaza ![]()
cu restrictiile
(8)
![]()
(9) ![]()
Metoda simplex presupune parcurgerea urmatorilor pasi.
Pas 1. Determinarea unei solutii de baza admisibile initiale. Constructia tabelului initial
Deoarece
![]() , rezulta ca solutia de baza obtinuta
prin considerarea celor m variabile
slack ca variabile de baza (corespund ultimilor m coloane ale matricei A, care sunt vectori liniar
independenti) si a variabilelor non-slack ca variabile non-baza,
, rezulta ca solutia de baza obtinuta
prin considerarea celor m variabile
slack ca variabile de baza (corespund ultimilor m coloane ale matricei A, care sunt vectori liniar
independenti) si a variabilelor non-slack ca variabile non-baza,
![]() ,
, ![]() ,,
,,![]()
este admisibila.
Din (4) rezulta,
(10)
![]()
si vom considera z drept variabila.
Tabelul initial, figurat mai jos, este construit astfel. In capul de tabel este trecut setul de variabile (inclusiv z). Primele linii corespund setului de constrangeri (5). Ultima linie, numita linia obiectiv, rezulta din (10). In partea stanga a tabelului sunt indicate variabilele de baza, iar in partea dreapta solutia de baza initiala si admisibila si valoarea functiei obiectiv.
Pentru exemplul 1, rezulta,
![]()
![]() ,
, ![]()
Solutia admisibila de baza la momentul initial este (0,0).
Din (7) obtinem,
![]()
si vom considera z drept variabila.
Tabelul initial este descris prin tabelul
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||
|
|
|
|
Tabelul 1
|
x |
y |
u |
v |
z | ||
|
u | ||||||
|
v | ||||||
Tabelul 2
Pas Verificarea criteriului de optimalitate
Pe baza relatiei (10), functia obiectiv este definita prin,
(11)
![]()
In relatia (11) un coeficient al primei sume este pozitiv daca elementul corespunzator din linia functiei obiectiv a tabelului 1 si care corespunde unei variabile non baza este negativ. Valoarea lui z poate fi marita prin cresterea valorii oricarei variabile non baza al carui corespondent in linia obiectiv este negativ. Este obtinut urmatorul criteriu de optimalitate.
Criteriul de oprire. Daca linia obiectiv a tabelului contine in pozitiile variabilelor non-baza elemente nenegative, atunci este obtinut maximul functiei obiectiv si calculul se incheie.
Pas 3. Selectarea coloanei pivotale (variabila de intrare)
Vom presupune in continuare ca nu este indeplinit criteriul de optimalitate, adica exista cel putin un element strict negativ in linia obiectiv si care corespunde unei variabile non-baza.
In aceasta etapa este determinata, pe baza punctului extrem dat, a unui punct extrem adiacent care sa determine obtinerea unei valori mai mari a functiei obiectiv. Acest lucru revine la selectarea unei variabile non-baza, VE, care va creste de la valoarea 0 si inlocuirea unei alte variabile de baza, care va scadea la valoarea 0. Variabila VE este numita de intrare, deoarece, la iteratia urmatoare, VE intra in setul variabilelor de baza. Coloana in care se gaseste VE este numita coloana pivotala.
Selectarea lui VE poate fi realizata in mai multe variante, doua dintre ele fiind prezentate in continuare.
1. Deoarece cea mai mare imbunatatire unitara este adusa functiei obiectiv prin selectarea acelei variabile cu proprietatea ca elementul corespunzator din linia obiectiv este negativ si cel mai mic cu aceasta proprietate, selecteaza ca variabila de intrare in sistem acea variabila. Daca exista mai multe cu aceasta proprietate, selecteaza aleator una dintre ele.
Regula Bland. Alege drept coloana pivotala prima coloana (cea cu indicele minim) cu element strict negativ in linia obiectiv.
Observatii
1. Regula Bland este utilizata daca algoritmul implementat prin utilizarea primei variante de alegere a coloanei pivotale cicleaza (numai daca este atinsa o solutie degenerata). Se numeste solutie degenerata o solutie in care cel putin o variabila de baza este nula.
In general obtinerea unei solutii degenerate nu determina neaparat ciclarea algoritmului simplex.
Pentru exemplul considerat, ca variabila de intrare poate fi aleasa x, ambele reguli de selectie fiind indeplinite in acest caz particular.
Pas 4. Selectarea liniei pivotale (variabila de iesire)
Pentru explicarea procedurii de selectare a variabilei care iese din setul variabilelor de baza, vom considera in continuare exemplul 1. Pe baza relatiilor (8), obtinem,
![]()
Deoarece y ramane setata pe valoarea 0, rezulta,
(12) ![]()
Din (12) obtinem ca x si u, respectiv x si v sunt invers proportionale, deci cresterea lui x determina descresterea valorilor lui u si v. Valoarea variabilei x poate fi marita pana cand una din variabilele u, v devine negativa. Pe baza relatiilor (9) si (12) obtinem,
![]() , deci
, deci

Cresterea
maxima a lui x este deci la
valoarea 3. Pentru ![]() , obtinem o noua solutie admisibila,
, obtinem o noua solutie admisibila,
![]()
care este solutie
de baza si adiacenta cu punctul extrem precedent. Noul set de
variabile primitve este ![]() . Variabila v
devine non-baza si este variabila de iesire (ea
paraseste setul variabilelor de baza). Linia variabilei de
iesire se numeste linie
pivotala.
. Variabila v
devine non-baza si este variabila de iesire (ea
paraseste setul variabilelor de baza). Linia variabilei de
iesire se numeste linie
pivotala.
Cresterea
variabilei de intrare este data de rapoartele dinte elementele de pe
coloana cea mai din dreapta (solutia admisibila de baza de la
momentul curent) si valorile corespunzatoare de pe coloana
pivotala (in cazul nostru, ![]() ), numite
), numite ![]() rapoarte. Cea mai mica
rapoarte. Cea mai mica ![]() ratie nenegativa (si nenula) este
valoarea maxim posibila cu care poate creste variabila de intrare;
variabila de baza care eticheteaza linia pentru care este atinsa
valoarea minima a
ratie nenegativa (si nenula) este
valoarea maxim posibila cu care poate creste variabila de intrare;
variabila de baza care eticheteaza linia pentru care este atinsa
valoarea minima a ![]() rapoartelor este variabila de iesire, linia
respectiva fiind linia pivotala. Daca nu exista nici un
rapoartelor este variabila de iesire, linia
respectiva fiind linia pivotala. Daca nu exista nici un ![]() raport nenegativ si nenul, variabila de intrare poate
creste oricat si problema de programare liniara nu are
solutie optima finita, caz in care algoritmul se opreste.
raport nenegativ si nenul, variabila de intrare poate
creste oricat si problema de programare liniara nu are
solutie optima finita, caz in care algoritmul se opreste.
Pas 5. Constructia noului tabel
In continuare este construit noul tabel pe exemplul considerat. Din a doua ecuatie a sistemului (8), obtinem,
![]() ,
,
![]()
si, inlocuind in prima ecuatie a sistemului (8), rezulta
![]()
Rezulta,
![]()
si, deoarece
in noua solutie de baza admisibila ![]() , obtinem
, obtinem ![]() .
.
Tabelul rezultat este,
|
x |
y |
u |
v |
z | ||
|
u |
|
|
| |||
|
x |
|
| ||||
Tabelul 3
La acest pas este construit tabelul rezultat in urma modificarii setului solutiilor de baza admisibile prin stabilirea variabilelor de intrare si de iesire. Procedura, numita de pivotare, este descrisa astfel.
Pas 5.1. Determina pivotul, k, elementul situat in pozitia (lp,cp), adica pe linia si coloana pivotala si marcheaza variabilele de intrare si iesire.
Pas
5. Multiplica linia pivotala cu ![]()
Pas
5.3. Elementele coloanei pivotale mai putin pivotul sunt modificate in 0
prin, efectuarea unei operatii primitive la nivel de linie: pentru fiecare
linie i, ![]() , adauga linia pivotala inmultita cu o
constanta, astfel incat elementul din pozitia (lp,cp) sa fie 0.
Constanta este determinata tinand cont de faptul ca noul pivot
este 1.
, adauga linia pivotala inmultita cu o
constanta, astfel incat elementul din pozitia (lp,cp) sa fie 0.
Constanta este determinata tinand cont de faptul ca noul pivot
este 1.
Pas 5.4. Inlocuieste in tabelul rezultat eticheta liniei pivotale cu variabila de intrare.
Dupa incheierea procedurii de pivotare, reia algoritmul de la pasul
Observatie. Tabelul 3 rezulta in urma aplicarii procedurii de pivotare tabelului
In continuare vom aplica algoritmul pentru exemplul considerat, pana la obtinerea solutiei optimale.
Valoarea
negativa nenula minima din linia obiectiv este -28, deci variabila de
intrare este y. Deoarece  , variabila de iesire este u. Linia pivotala este 1, coloana pivotala este 2 si
pivotul este
, variabila de iesire este u. Linia pivotala este 1, coloana pivotala este 2 si
pivotul este ![]() . Aplicarea procedurii de pivotare revine in continuare la
efectuarea urmatoarelor operatii,
. Aplicarea procedurii de pivotare revine in continuare la
efectuarea urmatoarelor operatii,
elementele din linia 1 sunt
impartite la ![]()
din linia 2 este scazuta
linia 1 inmultita cu ![]()
din linia 3 este scazuta linia 1 inmultita cu
Rezulta tabelul 4,
|
x |
y |
u |
v |
z | ||
|
y |
|
|
|
|||
|
x |
|
|
|
|||
Tabelul 4
Deoarece
nu exista elemente nenule si negative in linia obiectiv din tabelul 4,
rezulta ca a fost obtinuta solutia optimala ![]() si valoarea maxima a functiei obiectiv, 430.
si valoarea maxima a functiei obiectiv, 430.
Exemplul Fie problema de programare liniara,
Maximizeaza
![]()
cu restrictiile

Forma canonica este,
Maximizeaza
![]()
cu restrictiile

Tabelul initial este figurat in 5.
|
x |
y |
z |
u |
v |
t | ||
|
u | |||||||
|
v | |||||||
Tabelul 5
Variabila de intrare este y si variabila de iesire este v. Linia pivotala este 2, coloana pivotala este 2 si pivotul este 1. Aplicarea procedurii de pivotare revine in continuare la efectuarea urmatoarelor operatii,
din linia 1 este scazuta linia 2 inmultita cu
din linia 3 este scazuta linia 2 inmultita cu
Obtinem tabelul 6
|
x |
y |
z |
u |
v |
t | ||
|
u | |||||||
|
y | |||||||
Tabelul 6
Cea mai mica valoare negativa
este -8, dar nici un element
din coloana pivotala nu este pozitiv, deci nici un ![]() raport nu este pozitiv. Rezulta ca problema nu are
solutie optima finita.
raport nu este pozitiv. Rezulta ca problema nu are
solutie optima finita.
Variabile artificiale. Metoda in doua faze
In
sectiunea 1. este prezentata metoda simplex pentru rezolvarea
problemei de programare liniara data de relatiile (1), (2)
si (3) in ipoteza ![]() , care permite determinarea unei solutii de baza
admisibila la momentul initial. In continuare este descrisa o
procedura de introducere a unor variabile care sa poata fi
considerate variabile de baza, in cazul rezolvarii unei probleme de
programare liniara generala, in forma,
, care permite determinarea unei solutii de baza
admisibila la momentul initial. In continuare este descrisa o
procedura de introducere a unor variabile care sa poata fi
considerate variabile de baza, in cazul rezolvarii unei probleme de
programare liniara generala, in forma,
Maximizeaza
(9)
![]()
cu restrictiile
(10)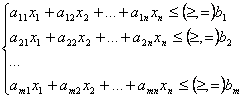
(11)
![]()
Fiecare inegalitate din sistemul de restrictii (10) poate fi transformata astfel incat membrul drept sa fie nenegativ, prin eventuala inmultire a inegalitatii cu -1. Inegalitatile sistemului (10) pot fi reordonate astfel incat (10) sa fie echivalent cu,

In
sistemele (12a) si (12b), inegalitatile sunt transformate in
egalitati prin introducerea variabilelor slack nenegative ![]() , respectiv
, respectiv ![]() , astfel,
, astfel,
pentru (12a):
(13a)
![]()
pentru (12b)
(13b)
![]()
Rezulta o problema de programare liniara in forma canonica,
Maximizeaza
(14) ![]()
cu restrictiile
(15)
![]()
(16)
![]()
si
astfel incat ![]() .
.
Determinarea unei solutii de baza admisibile poate fi realizata prin metoda in doua faze, descrisa in continuare.
Pentru
obtinerea unei solutii de baza fezabile, in sistemul (15) sunt
introduse m variabile, numite
artificiale si notate cu ![]() , obtinandu-se problema,
, obtinandu-se problema,
Maximizeaza
(17) ![]()
cu restrictiile
(18)
![]()
(19)
![]()
si
astfel incat ![]() .
.
Rezulta prin calcul direct ca un
vector ![]() Rs este
solutie admisibila a problemei definite de (14), (15) si (16)
daca si numai daca
Rs este
solutie admisibila a problemei definite de (14), (15) si (16)
daca si numai daca ![]() Rs+m este solutie
admisibila a problemei definite de (17), (18) si (19). Pentru
problema data prin (17), (18) si (19) o solutie de baza
admisibila care poate fi selectata initial este
Rs+m este solutie
admisibila a problemei definite de (17), (18) si (19). Pentru
problema data prin (17), (18) si (19) o solutie de baza
admisibila care poate fi selectata initial este ![]() . In continuare este dezvoltata o modalitate de
utilizare a algoritmului simplex pentru obtinerea unei solutii de
baza admisibila in care
. In continuare este dezvoltata o modalitate de
utilizare a algoritmului simplex pentru obtinerea unei solutii de
baza admisibila in care ![]() si, in
consecinta a unei solutii de baza admisibila a
problemei definite de (14), (15) si (16). Aceasta procedura este
constiutita in faza 1 a metodei.
si, in
consecinta a unei solutii de baza admisibila a
problemei definite de (14), (15) si (16). Aceasta procedura este
constiutita in faza 1 a metodei.
Faza 1. Deoarece in (19) fiecare ![]() este nenegativ, o modalitate de a ne asigura ca fiecare
este nenegativ, o modalitate de a ne asigura ca fiecare ![]() este nul este de a face suma variabilelor artificiale 0. Este
considerata, astfel, o problema auxiliara in care este
minimizata suma variabilelor artificiale cu seturile de restrictii (18)
si (19).
este nul este de a face suma variabilelor artificiale 0. Este
considerata, astfel, o problema auxiliara in care este
minimizata suma variabilelor artificiale cu seturile de restrictii (18)
si (19).
Daca minimul nu este nul, rezulta ca cel putin o variabila artificiala este nenula, deci strict pozitiva. In plus, nu toate valorile variabilelor artificiale pot fi 0, deoarece minimul sumei lor este strict pozitiv. In acest caz, problema originala nu are solutii admisibile.
In faza 1, sistemul problema de programare liniara in forma canonica definita prin (14), (15) si (16) este transformata conform (17), (18) si (19) si este introdusa noua problema, definita prin,
(20)
minimizeaza ![]()
cu restrictiile
(21)
![]()
(22)
![]()
si
astfel incat ![]() .
.
In
problema de minim (20) cu restrictiile (21) si (22), solutia de
baza admisibila initiala este selectata prin
considerarea vectorului ![]() , obtinut prin setarile,
, obtinut prin setarile,
![]() .
.
Justificarea
selectarii vectorului ![]() ca solutie de baza admisibila este
urmatoarea. Scrisa in forma matriceala, problema data
prin (20), (21) si (22) genereaza pe post de coloane
corespunzatoare variabilelor artificiala matricea unitate de ordin m, deci variabilele artificiale sunt
variabile de baza (ele corespund unui sistem liniar independent din
spatiul Rm).
ca solutie de baza admisibila este
urmatoarea. Scrisa in forma matriceala, problema data
prin (20), (21) si (22) genereaza pe post de coloane
corespunzatoare variabilelor artificiala matricea unitate de ordin m, deci variabilele artificiale sunt
variabile de baza (ele corespund unui sistem liniar independent din
spatiul Rm).
Pentru a aplica metoda simplex, problema de minim este transformata intr-o problema de maxim prin inmultirea cu -1 in relatia (20) si rezulta,
(23)
![]()
unde ![]() . Deoarece in metoda simplex variabilele de baza la
momentul initail sunt variabilele slack, cu coeficienti 0 in
functia obiectiv, trebuie ca variabilele artificiale sa fie inlocuite
in (23). Utilizand (21), obtinem,
. Deoarece in metoda simplex variabilele de baza la
momentul initail sunt variabilele slack, cu coeficienti 0 in
functia obiectiv, trebuie ca variabilele artificiale sa fie inlocuite
in (23). Utilizand (21), obtinem,
pentru
![]()
![]() si
si
(24)
![]() .
.
In continuare este rezolvata problema de programare liniara data prin (24), (21) si (22) prin aplicarea metodei simplex.
Daca minimul obtinut este 0, treci la faza La finalul fazei 1 fie variabilele artificiale sunt toate non baza, fie exista variabile artificiale de baza, dar cu valoare 0. In continuare este tratata prima situatie, cea de-a doua varianta fiind rezolvata cu ajutorul notiunii de dualitate prezentate in capitolul 3.
Faza Deoarece in solutia optimala obtinuta in urma aplicarii fazei 1 variabilele artificiale sunt toate non-baza, solutia poate fi utilizata ca solutie admisibila de baza in problema originala definita prin relatiile (14), (15) si (16). Tabelul final al fazei 1 devine tabel initial al fazei 2, cu urmatoarele modificari,
elimina coloanele etichetate cu variabilele artificiale;
calculeaza noua linie obiectiv astfel. Considera functia obiectiv definita de (14). Elementul liniei obiectiv ce corespunde unei variabile de baza este anulat prin adaugarea liniei variabilei de baza inmultita cu o constanta aleasa corespunzator.
Exemplul 3. Fie problema de programare liniara in forma canonica,
Maximizeaza
![]()
cu restrictiile

Faza 1. Sunt introduse variabilele artificiale ![]() si rezulta
problema auxiliara,
si rezulta
problema auxiliara,
(25)
Minimizeaza ![]()
cu restrictiile
(26)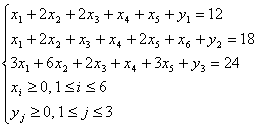
Pentru
transformarea problemei data prin relatiile (25) si (26) intr-o
problema de maxim, prin ![]() , rezulta functia obiectiv
, rezulta functia obiectiv
![]()
Pe baza relatiilor (26), rezulta

si functia obiectiv,
(27)
![]()
Solutia de baza admisibila la momentul initial este,
![]()
Tabelul initial este,
|
|
|
|
|
|
|
|
|
| ||
|
| ||||||||||
|
| ||||||||||
|
| ||||||||||
Tabelul 7
Variabila
de intrare este ![]() . Deoarece
. Deoarece ![]() , rezulta ca variabila care
paraseste sistemul este
, rezulta ca variabila care
paraseste sistemul este ![]() . Elementul pivotal este 6. Prin pivotare este
obtinut tabelul 8.
. Elementul pivotal este 6. Prin pivotare este
obtinut tabelul 8.
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
| |||||||
|
|
|
|
| |||||||
|
|
|
|
|
|
| |||||
|
|
|
|
Tabelul 8
Variabila
de intrare este ![]() . Deoarece
. Deoarece  , rezulta ca variabila care de iesire este
, rezulta ca variabila care de iesire este ![]() . Elementul pivotal este
. Elementul pivotal este ![]() . Prin pivotare rezulta tabelul 9.
. Prin pivotare rezulta tabelul 9.
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
| |||||||
|
|
|
|
| |||||||
|
|
|
|
|
| ||||||
|
|
|
|
Tabelul 9
Variabila
de intrare este ![]() . Deoarece este un singur
. Deoarece este un singur ![]() raport, rezulta ca variabila care de iesire
este
raport, rezulta ca variabila care de iesire
este ![]() . Pivotul este 1. Tabelul 10 este obtinut prin
pivotare.
. Pivotul este 1. Tabelul 10 este obtinut prin
pivotare.
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
| |||||||
|
|
|
|
| |||||||
|
|
|
|
|
| ||||||
Tabelul 10
Valoarea maxima a functiei obiectiv definita de relatia (27) este 0. Este obtinuta solutia de baza si admisibila pentru problema de optimizare initiala,
(28)
![]()
Faza a 2-a. Tabelul initial al fazei a doua este obtinut pe baza tabelului 10 astfel. Sunt eliminate coloanele corespunzatoare variabilelor artificiale. Functia obiectiv este definita prin,
(29)
![]()
Deoarece
solutia de baza admisibila la momentul initial este definita
de (28), rezulta ca variabilele ![]() sunt baza si, in linia obiectiv, elementele de pe
pozitiile 2, 3 si 6 terbuie sa fie nule. In acest scop, linia
obiectiv a tabelului 10, notata LO,
(considerat fara coloanele etichetate cu variabilele artificiale)
este prelucrata astfel:
sunt baza si, in linia obiectiv, elementele de pe
pozitiile 2, 3 si 6 terbuie sa fie nule. In acest scop, linia
obiectiv a tabelului 10, notata LO,
(considerat fara coloanele etichetate cu variabilele artificiale)
este prelucrata astfel:
a.
LO=LO-2*linia
3 (etichetata cu ![]()
b.
LO LO-3*linia 1
(etichetata cu ![]()
c. LO LO+2*linia 2 (etichetata
cu ![]()
Rezulta tabelul de la momentul initial (pentru problema initiala),
|
|
|
|
|
|
| ||
|
|
| ||||||
|
|
| ||||||
|
|
|
| |||||
|
|
Tabelul 11
Variabila
de intrare este ![]() . Deoarece este un singur
. Deoarece este un singur ![]() raport, rezulta ca variabila care de iesire
este
raport, rezulta ca variabila care de iesire
este ![]() . Pivotul este
. Pivotul este ![]() . Tabelul 12 este obtinut prin pivotare.
. Tabelul 12 este obtinut prin pivotare.
|
|
|
|
|
|
| ||
|
|
| ||||||
|
|
| ||||||
|
| |||||||
|
|
Deoarece linia obiectiv are toate elementele nenegative, rezulta ca valoarea maxima a functiei obiectiv (29) este 15 si o solutie optimala este,
![]() .
.
Observatie. Daca pentru problema initiala exista variabile ce
pot fi utilizate ca variabile de baza, atunci numarul variabilelor
artificiale scade. O variabila poate fi considerata de baza
daca apare intr-o singura constrangere a sistemului de restrictii al problemei de
programare liniara initiale, coeficientul sau fiind 1. De
exemplu, in problema rezolvata in 3,
variabila ![]() poate fi considerata de baza si sunt introduse
doar doua variabile artificiale.
poate fi considerata de baza si sunt introduse
doar doua variabile artificiale.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 8067
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved