| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
PROBLEMA DE PROGRAMARE LINIARA
Introducere
Programarea liniara este un domeniu dezvoltat la sfarsitul anilor 1940, odata cu necesitatea rezolvarii unor probleme de alocarea resurselor si a devenit un instrument esential al cercetarilor operationale, aplicat unor probleme extrem de variate din lumea reala.
In continuare vom prezenta problema de programare liniara prin intermediul catorva exemple. (Kolman, Beck, 1995)
Exemplul 1.1. Problema de transport
Un produs P este obtinut in doua fabrici situate in doua locatii, Bucuresti si Craiova si este stocat pentru desfacere in trei depozite, unul situat in Ploiesti, unul in Pitesti si unul la Cluj. Fabrica din Bucuresti produce saptamanal 120 de tone din produsul P, iar fabrica din Craiova produce P in cantitate de 140 tone pe saptamana. Pentru desfacerea produsului, necesarul saptamanal este: pentru depozitul din Ploiesti 100 de tone, pentru depozitul din Pitesti, 60 de tone, respectiv pentru depozitul din Cluj 80 de tone. In tabelul de mai jos sunt prezentate costurile de transport per tona de produs.
|
Ploiesti |
Pitesti |
Cluj |
|
|
Bucuresti | |||
|
Craiova |
Problema de rezolvat: calculul numarului de tone din produsul P care trebuie furnizate de cele doua fabrici fiecarui depozit astfel incat costul de transport sa fie minim si astfel incat sa fie respectate conditiile enuntate mai sus.
Modelul matematic.
Fie F1 si F2 fabricile din Bucuresti, respectiv Craiova si D1, D2 si D3 depozitele din Ploiesti, Pitesti si Cluj respectiv. Vom nota in continuare cu
![]() numarul de tone din produsul P aduse din Fi la Dj,
numarul de tone din produsul P aduse din Fi la Dj, ![]()
![]() costul de transport al unei tone din produsul P aduse din Fi la Dj,
costul de transport al unei tone din produsul P aduse din Fi la Dj, ![]()
Cantitatea
totala din produsul P care provine de la Fi este ![]() ,
, ![]() . Pe baza enuntului, rezulta,
. Pe baza enuntului, rezulta,
![]()
![]()
Cantitatea
totala din produsul P stocata de Dj, ![]() este
este ![]() . Deoarece solicitarile de produs la depozite este de
100, 60, respectiv 80 de tone, rezulta,
. Deoarece solicitarile de produs la depozite este de
100, 60, respectiv 80 de tone, rezulta,
![]()
![]()
![]()
Evident,
pentru ![]() ,
, ![]() .
.
Costul de transport, care trebuie minimizat, este,
![]() .
.
Este obtinut urmatorul model matematic,
Determina
valorile ![]() ,
,![]() care minimizeaza
care minimizeaza
![]()
cu restrictiile,
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]() ,
,
unde cantitatile maxime din produsul P care pot fi furnizate sunt
![]()
si necesarul de aprovizionat este, la nivelul fiecarui depozit,
![]() .
.
Exemplul 1.2. Problema financiara
Un investitor doreste sa investeasca exact 100.000 lei in doua titluri de valoare: T1, care plateste dividende de 7% si T2, din care rezulta dividende de 9%. Conditiile de efectuare a investitiei sunt:
suma investita in T1, ![]() , trebuie sa fie cel putin dublul sumei investite
in T2
, trebuie sa fie cel putin dublul sumei investite
in T2
suma investita in T2, ![]() , este de maxim 30.000 lei.
, este de maxim 30.000 lei.
Problema de rezolvat: determinarea sumelor de bani care vor fi investite in T1 si T2 astfel incat profitul obtinut de investitor sa fie maxim.
Modelul matematic.
Cu notatiile de mai sus, obtinem,
![]()
![]()
![]()
![]()
![]()
Profitul este calculat prin,
![]() .
.
Rezulta
urmatorul model matematic determina ![]() care maximizeaza
care maximizeaza
![]()
cu restrictiile,
![]()
![]()
![]()
![]()
![]()
1.2. Definirea problemei generice de programare liniara
Similar
formelor utilizate in exemplele prezentate in prima sectiune a
capitolului, problema generala de programare liniara poate fi
definita dupa cum urmeaza. Determina valorile ![]() care optimizeaza
(maximizeaza sau minimizeaza)
care optimizeaza
(maximizeaza sau minimizeaza)
(1.1)
![]()
cu restrictiile
(1.2)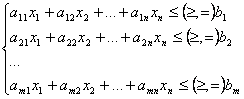
unde, in fiecare
inegalitate egalitate din sistemul (1.2), apare numai unul din simbolurile ![]()
Functia
liniara in variabilele ![]() definita in (1.1)
se numeste functie obiectiv.
Egalitatile sau inegalitatile care compun sistemul (1.2)
sunt referite drept restrictii.
definita in (1.1)
se numeste functie obiectiv.
Egalitatile sau inegalitatile care compun sistemul (1.2)
sunt referite drept restrictii. ![]() . Membrul stang al fiecarei restrictiii din (1.2)
este, la randul lui, functie liniara in variabilele
. Membrul stang al fiecarei restrictiii din (1.2)
este, la randul lui, functie liniara in variabilele ![]() . O problema in care fie functia obiectiv, fie
membrul drept al unei constrangeri sunt
functii neliniare este problema de programare neliniara.
. O problema in care fie functia obiectiv, fie
membrul drept al unei constrangeri sunt
functii neliniare este problema de programare neliniara.
Forma standard a unei probleme de programare liniara este definita astfel.
Determina valorile ![]() care
maximizeaza
care
maximizeaza
(1.3)
![]()
cu restrictiile
(1.4)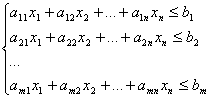
(1.5)
![]()
Forma canonica a unei probleme de programare liniara este definita astfel.
Determina valorile ![]() care
maximizeaza
care
maximizeaza
![]()
cu restrictiile

![]()
In continuare sunt prezentate modalitatile de exprimare a unei probleme de programare liniara oarecare in forma standard.
Exprimarea unei probleme de programare liniara in forma standard
Orice problema de minimizare poate fi transformata intr o problema de maxim, pe baza relatiei,
![]() .
.
Prin inmultirea unei inegalitati mai mare sau egal cu -1,
![]()
este obtinuta inegalitatea corespunzatoare "mai mic sau egal",
![]() .
.
Orice restrictie de tip egalitate poate fi transformata intr-o pereche de inegalitati, astfel. Relatia
![]()
este echivalenta cu perechea de inegalitati,
![]()
![]()
deci cu inegalitatile
![]()
![]() .
.
Daca
o variabila xj nu este
supusa constrangerii de a fi nenegativa, xj poate fi inlocuita cu perechea de variabile ![]() , unde
, unde
![]() ,
,
![]()
![]() .
.
Exemplul 1.3. Fie problema de programare liniara,
minimizeaza
![]()
cu restrictiile
![]()
![]()
![]()
Forma standard a problemei de mai sus este,
maximimeaza
![]()
cu restrictiile
![]()
![]()
![]()
![]()
![]()
![]()
In
exprimarea matriceala, o problema de programare liniara in forma
standard este descrisa astfel. Determina vectorul ![]() Rn care
maximizeaza
Rn care
maximizeaza
(1.6)
![]()
cu restrictiile
(1.7)
![]()
(1.8)
![]()
Un
vector ![]() Rn care
satisface restrictiiile problemei de programare liniara este numit solutie admisibila a
problemei. O solutie admisibila care optimizeaza functia
obiectiv a unei probleme de programare liniara se numeste solutie optimala.
Rn care
satisface restrictiiile problemei de programare liniara este numit solutie admisibila a
problemei. O solutie admisibila care optimizeaza functia
obiectiv a unei probleme de programare liniara se numeste solutie optimala.
In continuare vom prezenta modalitatea de transformare a unei probleme de programare liniara din forma standard in forma canonica
Exprimarea unei probleme de programare liniara standard in forma canonica
Orice problema de programare liniara standard poate fi exprimata in forma canonica pe baza urmatoarelor consideratii.
Fie restrictia
(1.9)
![]() .
.
Relatia
(1.9) poate fi exprimata in termenii unei egalitati prin
considerarea unei variabile suplimentare nenegative, ![]() ,
,
(1.10)
![]() .
.
Variabila
suplimentara ![]() desemneaza
diferenta dintre membrul drept si membrul stang al restrictiei definite
de (1.9) si se numeste variabila
slack.
desemneaza
diferenta dintre membrul drept si membrul stang al restrictiei definite
de (1.9) si se numeste variabila
slack.
Forma canonica a problemei de programare liniara exprimata in forma standard prin (1.3), (1.4) si (1.5) este,
Maximizeaza
(1.11)
![]()
cu restrictiile
(1.12)
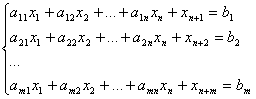
(1.13)
![]()
Noua problema obtinuta are un sistem cu m restrictii si n+m necunoscute.
Fie
![]() o solutie admisibila
a problemei de programare liniara
definita prin relatiile (1.3), (1.4) si (1.5). Pentru
o solutie admisibila
a problemei de programare liniara
definita prin relatiile (1.3), (1.4) si (1.5). Pentru ![]() este definita
variabila,
este definita
variabila,
![]() .
.
Evident,
pentru orice ![]() ,
, ![]() , deci vectorul
, deci vectorul ![]() satisface (1.12)
si (1.13), deci este o solutie admisibila a problemei exprimate
prin relatiile (1.11), (1.12) si (1.13).
satisface (1.12)
si (1.13), deci este o solutie admisibila a problemei exprimate
prin relatiile (1.11), (1.12) si (1.13).
Reciproc,
fie ![]() o solutie admisibila
a problemei exprimate prin relatiile (1.11), (1.12) si (1.13).
Rezulta ca
o solutie admisibila
a problemei exprimate prin relatiile (1.11), (1.12) si (1.13).
Rezulta ca ![]() si, deoarece
pentru orice
si, deoarece
pentru orice ![]() ,
, ![]() , obtinem ca
, obtinem ca
![]()
si, in
continuare, ca ![]() este o solutie admisibila
a problemei de programare liniara definita prin relatiile (1.3),
(1.4) si (1.5).
este o solutie admisibila
a problemei de programare liniara definita prin relatiile (1.3),
(1.4) si (1.5).
In
exprimarea matriceala, o problema de programare liniara in forma
canonica este descrisa astfel. Determina vectorul ![]() Rn care
maximizeaza
Rn care
maximizeaza
(1.14)
![]()
cu restrictiile
(1.15)
![]()
(1.16)
![]()
1.3. Geometria problemelor de programare liniara
Consideram in continuare problema de programare liniara in forma standard definita de (1.3), (1.4) si (1.5). Cea de a i a restrictie a problemei,
(1.17)
![]()
este exprimata in forma vectoriala prin,
![]() ,
,
unde ![]() . Multimea punctelor
. Multimea punctelor ![]() Rn care
satisfac (1.17) este semispatiu inchis al lui Rn.
Rn care
satisfac (1.17) este semispatiu inchis al lui Rn.
In cazul unei probleme de programare liniara in forma canonica, cea de a i a restrictie este definita de,
(1.18) ![]()
sau, echivalent,
![]()
Multimea
punctelor ![]() Rn care
satisfac (1.18) este un hiperplan al lui Rn.
Rn care
satisfac (1.18) este un hiperplan al lui Rn.
Observatii.
1. Hiperplanul definit de (1.18) este margine a semispatiului inchis (1.17).
2.
Hiperplanul definit de (1.18), ![]() , imparte Rn
in doua semispatii inchise,
, imparte Rn
in doua semispatii inchise,
![]()
![]()
cu proprietatile,
![]() Rn
Rn
![]()
3. Pe baza definitiei solutiei admisibile a problemei de programare liniara, P, rezulta ca multimea solutiilor admisibile ale lui P este intersectia tuturor hiperplanelor inchise definite de setul de restrictii ale lui P.
Exemple
1.4.
Fie ![]() restrictia
restrictia ![]() defineste semispatiul
inchis
defineste semispatiul
inchis ![]() , prezentat in figura 1.1.
, prezentat in figura 1.1.

1.5. Fie setul de restrictii ale unei probleme de programare liniara, exprimata in forma standard,

Multimea solutiilor admisibile ale problemei este figurata prin zona hasurata din figura 1.2.
Functia
obiectiv a unei probleme de programare liniara este ![]() . Fie k o
constanta. Graficul ecuatiei
. Fie k o
constanta. Graficul ecuatiei
![]()
este un hiperplan.
In ipoteza in care problema de optim este una de maxim, trebuie determinate
acele puncte ![]() Rn din
multimea solutiilor admisibile pentru care valoarea lui k este cea mai mare posibila. Din
punct de vedere geometric, acest lucru revine la determinarea unui hiperplan
care intersecteaza multimea solutiilor admisibile si pentru
care k este maxim.
Rn din
multimea solutiilor admisibile pentru care valoarea lui k este cea mai mare posibila. Din
punct de vedere geometric, acest lucru revine la determinarea unui hiperplan
care intersecteaza multimea solutiilor admisibile si pentru
care k este maxim.

Exemplul 1.6. Fie problema de programare liniara
Maximizeaza
![]()
cu restrictiile
![]()
![]()
![]()
![]()
In
figura 1.3 sunt prezentate multimea solutiilor admisibile (patrulaterul
cu varfurile (0,0), (3,0), ![]() , (0,4)) si hiperplanele
, (0,4)) si hiperplanele ![]() .
.
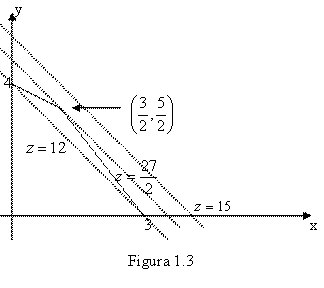
Graficele
prezentate in figura 1.3 sugereaza ca solutie punctul ![]() (Kolman, Beck, 1995).
(Kolman, Beck, 1995).
Teorema 1.1. Fie ![]() solutii admisibile
ale unei probleme de programare liniara P. Elementele multimii,
solutii admisibile
ale unei probleme de programare liniara P. Elementele multimii,
![]()
sunt solutii admisibile ale lui P.
Observatii
1. Pe baza teoremei 1.1, rezulta ca multimea solutiilor admisibile ale unei probleme de programare liniara este multime convexa.
2. Un semispatiu inchis este multime convexa.
3. Un hiperplan este multime convexa.
4. Intersectia unui numar finit de multimi convexe (daca nu este multimea vida) este multime convexa si se numeste poliedru convex.
5. Fie P o problema de programare liniara. Deoarece multimea solutiilor admisibile ale lui P, F, este intersectia tuturor hiperplanelor inchise definite de setul de restrictii ale lui P, rezulta ca F este poliedru convex (daca nu este multimea vida).
6. Multimea solutiilor unui sistem liniar de m ecuatii cu n necunoscute este convexa.
Definitia 1.1. O multime convexa se numeste marginita daca este inclusa intr-un dreptunghi, adica o multime de tipul
![]() ,
,
unde ![]() ,
, ![]() R,
R, ![]() . In caz contrar, multimea se numeste
nemarginita.
. In caz contrar, multimea se numeste
nemarginita.
Definitia 1.2. Un punct ![]() se numeste combinatie convexa a punctelor
se numeste combinatie convexa a punctelor
![]()
![]() daca exista
daca exista ![]() cu
cu
![]() ,
,
![]()
astfel incat
![]() .
.
Teorema 1.2. Multimea tuturor combinatiilor convexe definite pe un set finit de puncte din Rn este convexa.
Definitia 1.3. Fie S o multime
convexa. Un punct ![]() se numeste punct
extrem al lui S daca, pentru
orice pereche de puncte distincte
se numeste punct
extrem al lui S daca, pentru
orice pereche de puncte distincte ![]() ,
,
![]()
Exemplul 1.7. Punctele de extrem ale multimii convexe din figura 1.4 sunt A, B, C si D.
Teorema 1.3. Fie S o multime
convexa in Rn. Un
element ![]() este punct extrem daca si numai daca nu este
combinatie convexa a nici unui subset al lui S (care nu contine u).
este punct extrem daca si numai daca nu este
combinatie convexa a nici unui subset al lui S (care nu contine u).
Teorema 1.4 (Teorema de punct extrem) Fie S multimea solutiilor admisibile ale unei probleme de programare liniara P.
1. Daca S este nevida si marginita, atunci exista o solutie optimala a problemei P si aceasta este punct extrem al lui S.
2. Daca S este nevida si nemarginita si P are o solutie optimala a problemei, atunci aceasta este punct extrem al lui S.
3. Daca P nu are solutie optimala, atunci S este fie vida, fie nemarginita.

Exemple
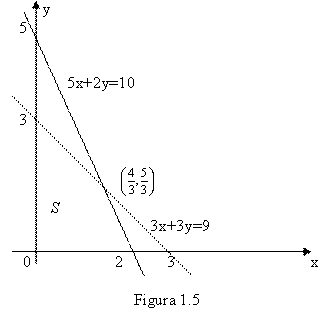
1.8. Fie problema de optimizare liniara,
Maximizeaza
![]()
cu restrictiile
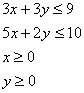
In
figura 1.5 este prezentata multimea solutiilor admisibile, S. S
este marginita si punctele extrem sunt ![]() . Pe baza teoremei de punct extrem, rezulta ca o
solutie optimala este in multimea
. Pe baza teoremei de punct extrem, rezulta ca o
solutie optimala este in multimea ![]() . Deoarece
. Deoarece ![]() , rezulta ca valoarea maxima a lui f este 24 si o solutie
optimala este
, rezulta ca valoarea maxima a lui f este 24 si o solutie
optimala este ![]() .
.
1.9. Fie problema de optimizare liniara
Maximizeaza
![]()
cu restrictiile
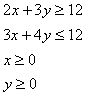
In aceasta situatie multimea solutiilor admisibile este vida, restrictiile fiind conflictuale.
1.10 Fie problema de optimizare liniara,
Maximizeaza
![]()
cu restrictiile
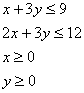
In
figura 1.6 este prezentata multimea solutiilor admisibile, S. S
este marginita si punctele extrem sunt ![]() . Pe baza teoremei de punct extrem, rezulta ca o
solutie optimala este in multimea
. Pe baza teoremei de punct extrem, rezulta ca o
solutie optimala este in multimea ![]() . Deoarece
. Deoarece ![]() , rezulta ca valoarea maxima a lui f este 12 si B si C sunt
solutii optimale.
, rezulta ca valoarea maxima a lui f este 12 si B si C sunt
solutii optimale.
Punctele
de pe segmentul de dreapta ![]() , definite de,
, definite de,
(1.19)
![]()
sunt solutii
optimale ale problemei. Intr-adevar, pentru ![]() definit de (1.19),
obtinem,
definit de (1.19),
obtinem,
![]() .
.

1.4. Solutiile de baza ale problemelor de programare liniara
In 1.3 este prezentata o modalitate de calcul a unei solutii optimale a unei probleme de programare liniara pe baza punctelor extrem. Metoda prezentata este in general utila in cazul problemelor cu maxim 3 variabile, solutiile problemelor cu mai mult de 3 variabile neputand fi calculate geometric in mod direct. Pentru usurarea calculului punctelor extrem, este descrisa reprezentarea algebrica, pe baza notiunii de solutie de baza a unei probleme de programare liniara.
Consideram in continuare problema de programare liniara in forma canonica, definita prin,
(1.20)
Maximizeaza ![]()
cu restrictiile
(1.21)
![]()
(1.22)
![]()
unde ![]() Rs,
Rs, ![]() Rm, A este matrice
Rm, A este matrice ![]() . Fie A1,
A2,, As vectorii care
reprezinta coloanele matricei A.
Relatia (1.21) poate fi exprimata prin,
. Fie A1,
A2,, As vectorii care
reprezinta coloanele matricei A.
Relatia (1.21) poate fi exprimata prin,
(1.23)
![]() ,
,
unde ![]() .
.
Dezvoltarea prezentata in continuare este realizata in ipotezele
1.![]()
2. m coloane ale lui A sunt liniar independente (rangul lui A este m).
Observatie. Ipotezele de lucru mai sus mentionate sunt indeplinite in situtia in care problema de programare liniara in forma canonica provine dintr-o problema de programare liniara in forma standard (vezi 1.2).
Multimea celor m coloane liniar independente ale matricei A formeaza o baza in Rm. Vom considera in continuare o renumerotare a coloanelor lui A astfel incat ultimile m coloane sa fie liniar independente si fie S multimea solutiilor admisibile ale problemei definite de (1.20), (1.21) si (1.22).
Teorema 1.5. Daca ![]() sunt ultimile m
coloane ale lui A si sunt
liniar independente si daca
sunt ultimile m
coloane ale lui A si sunt
liniar independente si daca
![]() ,
,
unde ![]() , atunci
, atunci ![]() este punct extrem al
lui S. (Kolman, Beck, 1995)
este punct extrem al
lui S. (Kolman, Beck, 1995)
Teorema 1.6. Daca ![]() este punct extrem al
lui S, atunci coloanele matricei A care corespund componentelor strict pozitive
ale lui x formeaza un set de
vectori liniar independenti in Rm.
(Kolman, Beck, 1995)
este punct extrem al
lui S, atunci coloanele matricei A care corespund componentelor strict pozitive
ale lui x formeaza un set de
vectori liniar independenti in Rm.
(Kolman, Beck, 1995)
Corolarul 1.1. Daca ![]() este punct extrem al
lui S si
este punct extrem al
lui S si ![]() sunt r componente
strict pozitive ale lui x, atunci
sunt r componente
strict pozitive ale lui x, atunci ![]() si setul de coloane
si setul de coloane ![]() care corespund componentelor
care corespund componentelor ![]() pot fi extinse la un set de m vectori liniar independenti in Rm prin adaugarea a m-r coloane
corespunzator alese din matricea A.
(Kolman, Beck, 1995)
pot fi extinse la un set de m vectori liniar independenti in Rm prin adaugarea a m-r coloane
corespunzator alese din matricea A.
(Kolman, Beck, 1995)
Teorema 1.7. Cu notatiile de pana acum, rezulta ca orice punct extrem al multimii S are cel mult m componente strict pozitive, restul fiind nule. (Kolman, Beck, 1995)
Observatie. Daca rangul matricei A este m, rezulta ca vectorii care formeaza liniile lui A sunt liniar independenti. Rezulta ca sistemul constrangerilor nu contine ecuatii redundante.
Fie
sistemul cu m ecuatii si s necunoscute definit de (1.21), cu ![]() . Presupunem ca matricea A are m coloane vectori
liniar independenti si fie
. Presupunem ca matricea A are m coloane vectori
liniar independenti si fie ![]() o multime de m coloane liniar independente ale lui A. Seteaza pe 0 cele s-m variabile ce corespund coloanelor
matricei A dar care nu apartin
lui T. Pe baza reprezentarii
(1.23) a sistemului (1.21), rezulta reprezentarea,
o multime de m coloane liniar independente ale lui A. Seteaza pe 0 cele s-m variabile ce corespund coloanelor
matricei A dar care nu apartin
lui T. Pe baza reprezentarii
(1.23) a sistemului (1.21), rezulta reprezentarea,
(1.24)
![]()
Relatia (1.24) defineste un sistem de m ecuatii cu m necunoscute, cu solutie unica.
Definitia 1.4. Se numeste solutie de baza vectorul format cu cele m valori obtinute in urma rezolvarii sistemului (1.24), numite variabile de baza, si cu s-m componente nule, numite variabile non-baza.
Definitia 1.5. Se numeste solutie de baza admisibila a problemei de programare liniara definita de (1.20), (1.21) si (1.22) o solutie de baza cu proprietatea ca este solutie admisibila (o solutie de baza care indeplineste si conditia de nenegativitate (1.22)).
Teorema 1.8. Fie P problema de programare liniara definita de (1.20), (1.21) si (1.22) si S multimea solutiilor admisibile ale lui P. Orice solutie de baza si admisibila a lui P este punct extrem al lui S si, reciproc, orice punct exterm al lui S este solutie de baza si admisibila a lui P. (Kolman, Beck, 1995)
Teorema 1.9. Fie P problema de
programare liniara definita de (1.20), (1.21) si (1.22). P are un numar finit de
solutii de baza si admisibile, inferior lui ![]() , care reprezinta numarul solutiilor de baza
ale lui P.
, care reprezinta numarul solutiilor de baza
ale lui P.
Fie P problema de programare liniara in forma standard definita de (1.6), (1.7) si (1.8), S multimea solutiilor admisibile ale lui P si S' multimea solutiilor admisibile ale variantei canonice ale lui P. Urmatoarea teorema stabileste relatia dintre S si S'.
Teorema 1.10. Orice punct extrem al lui S determina obtinerea unui punct extrem al lui S' prin adaugarea variabilelor slack. Reciproc, orice punct extrem al lui S determina, prin trunchiere (eliminarea variabileleo slack), obtinerea unui punct extrem al lui S.
Teorema 1.11. Multimea convexa a solutiilor admisibile ale unei probleme de programare liniara in forma standard are un numar finit de puncte extreme.
Prin utilizarea teoremelor 1.4 si 1.11 este obtinuta urmatoarea procedura de rezolvare a unei probleme de programare liniara in forma standard, P.
Pas 1. Determina P , forma canonica a problemei P.
Pas 2. Calculeaza multimea solutiilor de baza si selecteaza S', subsetul solutiilor admisibile de baza ale lei P'.
Pas 3. Selecteaza solutiile optimale din setul S si determina solutiile optimale ale lui P prin trunchiere.
Exemplul 1.11. Fie problema de programare linira in forma standard,
Maximizeaza
![]()
cu restrictiile

Forma canonica rezulta prin introducerea a doua variabile slack, u,v,
Maximizeaza
![]()
cu restrictiile

Multimea solutiilor de baza rezulta prin considerarea tuturor variantelor de 2 coloane liniar independente, astfel.
Primele doua coloane ale lui A sunt liniar independente;vom selecta
ca variabile primitve x si y, iar variabilele u si v sunt non-baza.
Rezulta ![]() si solutia de
baza
si solutia de
baza ![]() . Solutia obtinuta este admisibila (toate
componentele sunt pozitive).
. Solutia obtinuta este admisibila (toate
componentele sunt pozitive).
Coloanele 1 si 3 sunt liniar independente. Variabilele de baza
sunt x si u, iar variabilele non-baza sunt y si v. Rezulta
solutia de baza ![]() , care este admisibila.
, care este admisibila.
Coloanele 1 si 4 sunt liniar independente. Variabilele de baza
sunt x si v, iar variabilele non-baza sunt y si u. Rezulta
solutia de baza ![]() , care nu este admisibila (ultima componenta este
negativa).
, care nu este admisibila (ultima componenta este
negativa).
Coloanele 2 si 3 sunt liniar independente. Variabilele de baza
sunt y si u, iar variabilele non-baza sunt x si v. Rezulta
solutia de baza ![]() , care nu este admisibila.
, care nu este admisibila.
Coloanele 2 si 4 sunt liniar independente. Variabilele de baza
sunt y si v, iar variabilele non-baza sunt x si u. Rezulta
solutia de baza ![]() , care este admisibila.
, care este admisibila.
Ultimile doua coloane ale lui
A sunt liniar independente;vom
selecta ca variabile de baza u si
v, iar variabilele x si y sunt non-baza. Rezulta ![]() si solutia de
baza
si solutia de
baza ![]() , care este solutie admisibila.
, care este solutie admisibila.
Multimea solutiilor baza admisibile, deci a punctelor extreme ale multimii solutiilor admisibile ale problemei de programare liniara in forma canonica este,
![]()
![]()
maximul
functiei obiectiv este 430 si se atinge pentru ![]() , care este o solutie optimala a problemei in forma
canonica. Pentru problema initiala, rezulta solutia
optimala prin trunchierea punctului
, care este o solutie optimala a problemei in forma
canonica. Pentru problema initiala, rezulta solutia
optimala prin trunchierea punctului![]() cu variabile de baza x
si y,
cu variabile de baza x
si y, ![]() .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2249
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved