| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
In cele ce urmeaza se prezinta un algoritm ce rezolva problema de transport cu valori fuzzy pentru cerere si oferta si cu conditia de integralitate impusa solutiei. Algoritmul este exact si efectiv calculabil desi problema se formuleaza intr-o maniera generala, adica valorile fuzzy pentru cerere si oferta pot fi diferite unele de celelalte si sunt numere fuzzy de un anumit fel.
Introducere
Modelul de transport are largi aplicatii, nu doar in problema de transport in sine, dar si in problema de planificare a productiei.
Parametrii fiecarei probleme de transport sunt costuri unitare (profiturile) si valorile pentru cerere si oferta (productie, capacitate de depozitare). In practica acesti parametrii nu sunt intotdeauna cunoscuti si stabili. In problema abordata in continuare se presupune ca costurile unitare (profiturile) sunt exact cunoscute dar estimarea valorilor pentru cerere si oferta (capacitati) este aproximativa. Aceasta imprecizie rezulta fie din lipsa de informatie, fie dintr-o anumita flexibilitate in planificarea capacitatilor intreprinderii considerate. Un mijloc frecvent utilizat pentru a exprima imprecizia sunt numerele fuzzy.
In problema de transport clasica cu valori intregi pentru cerere si oferta exista intotdeauna o solutie intreaga. Aceasta solutie poate fi determinata cu metoda simplex de transport, una dintre cele mai utilizate metode de rezolvare a problemelor de transport. Aceasta proprietate (posibilitatea gasirii unei solutii intregi) nu este pastrata in problema de transport fuzzy cu valori fuzzy pentru cerere si oferta, chiar daca caracteristicile numerelor fuzzy existente in problema sunt intregi.
Pentru a obtine o solutie intreaga optimala (care ar putea fi necesara din ratiuni de flexibilitate) se utilizeaza un algoritm special. Un astfel de algoritm este prezentat in S.Chanas si D.Kuchta. In cele ce urmeaza se propune un algoritm ce determina solutia intreaga optimala a unei probleme fuzzy de transport, mai generala decat cea considerata in S.Chanas si D.Kuchta, utilizand doar problema de transport clasica (neparametrica).
Formularea problemei si notatiile folosite
Numerele fuzzy considerate aici sunt de tip ![]() . Un numar fuzzy de tip
. Un numar fuzzy de tip ![]() se noteaza astfel
se noteaza astfel ![]() si are functia
caracteristica:
si are functia
caracteristica:

unde ![]() si
si ![]() sunt functii de forma.
sunt functii de forma.
F
este o functie de forma daca: F continua, necrescatoare pe ![]() ,
, ![]() si strict
descrescatoare pe acea parte a domeniului pe care este pozitiva.
si strict
descrescatoare pe acea parte a domeniului pe care este pozitiva.
Exemple:
Liniara:
![]() .
.
Exponentiala:
![]() .
.
Putere:
![]() .
.
Rationala:
![]()
Exista si cazuri particulare in care
functiile ![]() si
si ![]() nu au nici o
semnificatie.
nu au nici o
semnificatie.
![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() .
.
Problema de transport fuzzy pe care o consideram aici se enunta astfel:
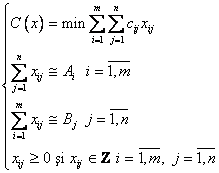 (2.1)
(2.1)
unde ![]() ,
, ![]() sunt numere fuzzy de
forma:
sunt numere fuzzy de
forma:
![]()
![]()
![]()
![]()
![]() este o solutie
matriceala (ale carui componente sunt variabile decizionale corespunzatoare)
adica
este o solutie
matriceala (ale carui componente sunt variabile decizionale corespunzatoare)
adica ![]() . Costurile unitare de transport
. Costurile unitare de transport ![]() ,
, ![]() ,
, ![]() sunt presupuse a fi
numere crisp.
sunt presupuse a fi
numere crisp.
Aceasta formulare a problemei arata ca
rezultatul este exprimat tot printr-un numar fuzzy notat cu ![]() , de forma:
, de forma:
![]()
Aceasta problema este mai completa decat cea
tratata in S.Chanas si D.Kuchta. Complexitatea consta din urmatoarele: aici
perechile ![]() ,
, ![]() si
si ![]() ,
, ![]() pot fi diferite, in
timp ce in S.Chanas si D.Kuchta trebuie sa fie indice.
pot fi diferite, in
timp ce in S.Chanas si D.Kuchta trebuie sa fie indice.
In definitia urmatoare se defineste conceptul de constrangere fuzzy si conceptul de obiectiv fuzzy.
Definitia 2.1
Fie
![]() o solutie arbitrara a
problemei (2.1).
o solutie arbitrara a
problemei (2.1).
a) Valoarea 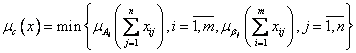 se numeste gradul de
satisfacere a restrictiilor pentru problema (2.1).
se numeste gradul de
satisfacere a restrictiilor pentru problema (2.1).
b) 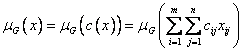 se numeste gradul de
satisfacere a obiectivului (rezultatul problemei (2.1) prin
se numeste gradul de
satisfacere a obiectivului (rezultatul problemei (2.1) prin ![]() .
.
Conform abordarii Belmann-Zadeh o solutie se numeste solutie optimala daca este o solutie a unei probleme in care restrictiile si obiectivul sunt de grad maxim.
Definitia 2.2
Solutia
maximizanta este un vector ![]() pentru care
pentru care ![]() atinge maximul. Daca
valoarea maxima este 0 se spune ca problema (2.1) este nerezolvabila.
atinge maximul. Daca
valoarea maxima este 0 se spune ca problema (2.1) este nerezolvabila.
Solutia problemei
Conform cu definitia 2.1 a rezolva problema 2.1 este echivalent cu a rezolva urmatoarea problema de programare matematica:
![]()
![]()
A rezolva aceasta problema de programare matematica este echivalent cu a rezolva urmatoarea problema:
 (2.2)
(2.2)
Pentru a intelege cele ce urmeaza se reaminteste urmatoarea definitie:
Definitia 2.3
Fie ![]() un numar fuzzy
un numar fuzzy ![]() (notata
(notata ![]() ) este
) este ![]() .
.
Tinand cont de aceasta definitie se observa
usor ca ipotezele asupra lui ![]() si
si ![]() considerate in aceasta
problema,
considerate in aceasta
problema, ![]() - taieturile
- taieturile ![]() si
si ![]() sunt intervale de
forma:
sunt intervale de
forma:
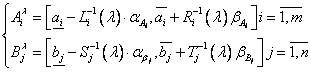 (2.3)
(2.3)
![]() - taietura pentru
obiectivul fuzzy
- taietura pentru
obiectivul fuzzy ![]() este multimea:
este multimea:
![]() (2.4)
(2.4)
Tinand cont de acestea problema (2.2) poate fi rescrisa astfel:
 (2.5)
(2.5)
Problema anterioara nu este o problema de transport datorita functiei sale obiectiv si a primei conditii. Din acest motiv nu putem folosi unul din algoritmii de transport pentru a o rezolva. Ii putem asocial insa o problema de transport interval. In plus, solutia acestei probleme auxiliare permite gasirea solutiei problemei (2.5) si de aici a problemei (2.1).
Aceasta problema auxiliara are urmatoarea forma:
 (2.6)
(2.6)
Rezolvarea problemei (2.6) pentru ![]() fixat, permite sa se
afle daca (2.5) este posibila pentru aceasta valoare a lui
fixat, permite sa se
afle daca (2.5) este posibila pentru aceasta valoare a lui ![]() . Este suficient sa se verifice daca valoarea functiei
obiectiv a problemei (2.6) verifica prima conditie din (2.5).
. Este suficient sa se verifice daca valoarea functiei
obiectiv a problemei (2.6) verifica prima conditie din (2.5).
Ceea ce este necesar este valoarea maxima a
lui ![]() pentru care (2.5) este
posibila si solutia corespunzatoare a lui (2.5).
pentru care (2.5) este
posibila si solutia corespunzatoare a lui (2.5).
Capetele intervalelor ce apar in conditiile problemei (2.6) pot sa nu fie intregi. Aceasta ar insemna ca dupa trecerea la problema de transport clasica descrisa in (2.6) am putea avea o problema clasica de transport cu valori ale cereri si/sau ofertei ne-intregi, ceea ce face ca algoritmul clasic sa nu garanteze obtinerea unei solutii intregi. Totusi se poate inlocui problema (2.6) cu o problema (2.7), ce are deja capetele intregi pentru intervalele cerere si oferta fara a schimba multimea solutiilor posibile si optimale.
In definirea problemei (2.7) se foloseste urmatoarea notatie:
Definitia 2.4
Fie
![]() un interval.
un interval.![]() - este cel mai mare
interval cu capete intregi ce este continut in
- este cel mai mare
interval cu capete intregi ce este continut in ![]() . Adica:
. Adica: ![]() , unde
, unde ![]() ,
, ![]() .
.
Cu aceasta notatie problema (2.7) care inlocuieste problema (2.6) are urmatoare forma:
 (2.7)
(2.7)
Multimile solutiilor posibile si
optimale ale lui (2.6) si (2.7) sunt identice datorita conditiei de integralitate
impusa lui ![]() .
.
Pentru ![]() fixat, se poate
rezolva (2.5) inlocuind-o cu una clasica cu valori intregi pentru cerere si
oferta si se poate aplica de exemplu algoritmul problemei simplex de transport.
fixat, se poate
rezolva (2.5) inlocuind-o cu una clasica cu valori intregi pentru cerere si
oferta si se poate aplica de exemplu algoritmul problemei simplex de transport.
Daca se poate rezolva (2.7) (sau
problema clasica de transport corespunzatoare) ca o problema cu parametru ![]() , se va putea, de asemenea, sa se rezolve cea initiala.
, se va putea, de asemenea, sa se rezolve cea initiala.
Totusi, coeficientii problemei depind
de ![]() neliniar ceea ce
determina o oarecare dificultate. Pentru a evita rezolvarea unei probleme
parametrice de transport se propune urmatorul algoritm ce necesita doar
rezolvarea a catorva probleme de transport clasice.
neliniar ceea ce
determina o oarecare dificultate. Pentru a evita rezolvarea unei probleme
parametrice de transport se propune urmatorul algoritm ce necesita doar
rezolvarea a catorva probleme de transport clasice.
Algoritmul incepe de la cele mai mari
valori ale lui ![]() , inseamna ca
, inseamna ca ![]() si
si ![]() . Se investigheaza pentru care valori ale lui
. Se investigheaza pentru care valori ale lui ![]() , (2.5) este admisibila.
, (2.5) este admisibila.
Daca este imposibila pentru ![]() , (2.1) este imposibila.
, (2.1) este imposibila.
Daca (2.5) este posibila pentru ![]() atunci
atunci ![]() valoarea optimala a
functiei obiectiv in (2.5) si solutia corespunzatoare a lui (2.5) este si
solutie pentru problema (2.1).
valoarea optimala a
functiei obiectiv in (2.5) si solutia corespunzatoare a lui (2.5) este si
solutie pentru problema (2.1).
Daca (2.5) este posibila pentru ![]() si imposibila pentru
si imposibila pentru ![]() (cel mai frecvent
caz), se considera
(cel mai frecvent
caz), se considera ![]() si apoi
si apoi ![]() .
.
Procedand astfel ne vom apropia din ambele parti
de valoarea optimala a functiei obiectiv a lui (2.5). Astfel la fiecare pas se considera ![]() astfel incat (2.5)
este posibila pentru
astfel incat (2.5)
este posibila pentru ![]() si imposibila pentru
si imposibila pentru ![]() . Nu are rost sa se subimparta acest interval, cand (2.7)
pentru
. Nu are rost sa se subimparta acest interval, cand (2.7)
pentru ![]() este o extensie minima
a lui (2.7) pentru
este o extensie minima
a lui (2.7) pentru ![]() (ca in definitia 2.5).
(ca in definitia 2.5).
Definitia 2.5
Problema
(2.7) pentru ![]() este o extindere
minimala cand problema (2.7) pentru
este o extindere
minimala cand problema (2.7) pentru ![]() este identica cu
problema 2.7) pentru
este identica cu
problema 2.7) pentru ![]() unde:
unde:
![]()
Din secventa
anterioara rezulta ca algoritmul corespunzator (in care intervalele consecutive ale valorilor se
subimpart in doua) se termina dupa un numar finit de pasi, daca verificam la
fiecare pas daca problema (2.7) pentru ![]() este o extindere
minimala a problemei (2.7) pentru
este o extindere
minimala a problemei (2.7) pentru ![]() .
.
Utilizatorul poate determina
![]() , incepand cu acele conditii ce trebuie verificate.
, incepand cu acele conditii ce trebuie verificate.
Algoritmul se prezinta astfel:
Pasul 1
Punem
![]() ,
, ![]() .
.
Pasul 2
Rezolvam
problema (2.7) pentru ![]() . Daca problema este posibila si
. Daca problema este posibila si ![]() se trece la pasul 3.
Altfel problema (2.1) este imposibila.
se trece la pasul 3.
Altfel problema (2.1) este imposibila.
Deci STOP (problema (2.1) imposibila si ![]() oricare ar fi
oricare ar fi ![]() ).
).
Pasul 3
Rezolvam
problema (2.7) pentru ![]() . Daca problema este posibila si
. Daca problema este posibila si ![]() atunci STOP si
atunci STOP si ![]() este solutia optimala
a problemei (2.1) si
este solutia optimala
a problemei (2.1) si ![]() . Altfel, se trece la pasul 4.
. Altfel, se trece la pasul 4.
Pasul 4
Luam
![]() si se trece la pasul
5.
si se trece la pasul
5.
Pasul 5
Se
rezolva problema (2.7) pentru ![]() . Daca problema este imposibila atunci
. Daca problema este imposibila atunci ![]() si se trece la pasul 6.
Altfel exista trei cazuri posibile:
si se trece la pasul 6.
Altfel exista trei cazuri posibile:
i) ![]() , rezulta
, rezulta ![]() este solutie optimala
a problemei (2.1) si STOP.
este solutie optimala
a problemei (2.1) si STOP.
ii)![]() , atunci se pune
, atunci se pune ![]() si se trece la pasul
6.
si se trece la pasul
6.
iii) ![]() , se pune
, se pune ![]() sau daca
sau daca ![]() se trece la pasul 6.
se trece la pasul 6.
Pasul 6
Daca
![]() se trece la pasul 4. Altfel
se verifica daca problema (2.7) pentru
se trece la pasul 4. Altfel
se verifica daca problema (2.7) pentru ![]() este extensie minimal
a problemei (2.7) pentru
este extensie minimal
a problemei (2.7) pentru ![]() . Daca nu, se trece la pasul 4. Altfel STOP. O solutie
. Daca nu, se trece la pasul 4. Altfel STOP. O solutie ![]() sau
sau ![]() este optimala pentru
problema (2.1).
este optimala pentru
problema (2.1).
Daca problema (2.5)
este imposibila pentru ![]() atunci
atunci ![]() este solutie optimala
pentru problema (2.1).
este solutie optimala
pentru problema (2.1). ![]() este dat de utilizator
este dat de utilizator
![]() .
.
Transformarea unei probleme de transport interval intr-una clasica
Se considera problema:
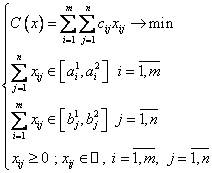 (2.8)
(2.8)
Problema (2.8) poate fi transformata intr-o problema clasica de transport unde valorile pentru cerere si oferta sunt reale adaugand originile si destinatiile cu nivele pentru cerere si oferta potrivite ca in problema de transport cu restrictii de tip interval. Problema clasica de transport corespunzatoare se defineste astfel:
Exista ![]() origini cu valori ale
ofertei
origini cu valori ale
ofertei ![]() :
:
![]() ,
, ![]()
![]() ,
, ![]()
![]()
Exista ![]() destinatii cu
urmatoarele valori ale cererii:
destinatii cu
urmatoarele valori ale cererii:
![]() ,
, ![]()
![]() ,
, ![]()
![]()
Coeficientii de cost ![]() se vor defini astfel:
se vor defini astfel:
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
![]() este un numar mai
mare, caci ruta corespunzatoare este intensiva pentru
este un numar mai
mare, caci ruta corespunzatoare este intensiva pentru ![]() .
.
![]() pentru
pentru ![]() .
.
![]() este un numar mai
mare, caci ruta corespunzatoare pentru
este un numar mai
mare, caci ruta corespunzatoare pentru ![]() este intensiva.
este intensiva.
![]() pentru
pentru ![]() .
.
Odata ce s-a
determinat o solutie ![]() a problemei auxiliare
clasice definita mai sus, se poate obtine solutia problemei (2.8) astfel:
a problemei auxiliare
clasice definita mai sus, se poate obtine solutia problemei (2.8) astfel:
Pentru ![]() si
si ![]() :
: ![]()
Pentru ![]() si
si ![]() :
: ![]()
Exemplu numeric
Algoritmul este ilustrat prin urmatorul exemplu.
Sa se minimizeze
![]()
![]()

Obiectivul fuzzy este
determinat prin urmatorul numar fuzzy ![]() .
. ![]() inlocuieste functia de
forma liniara;
inlocuieste functia de
forma liniara; ![]() exponentiala cu
parametrul
exponentiala cu
parametrul ![]() ;
; ![]() functia de forma
putere cu parametrul
functia de forma
putere cu parametrul ![]() ;
; ![]() rationala cu
parametrul
rationala cu
parametrul ![]() .
. ![]() - taieturile pentru
valorile fuzzy ale ofertelor si ale cererilor, precum si ale obiectivului fuzzy
cu functiile de forma considerata sunt (se tine cont de (2.3) si (2.4)):
- taieturile pentru
valorile fuzzy ale ofertelor si ale cererilor, precum si ale obiectivului fuzzy
cu functiile de forma considerata sunt (se tine cont de (2.3) si (2.4)):
![]()
![]()
![]()
![]()
![]()
![]()
Pasii algoritmului sunt:
Pasul 1
![]() ,
, ![]()
Pasul 2
Problema
(2.7) este posibila pentru ![]() si
si ![]() , unde
, unde ![]() .
.
Pasul 3
Problema
(2.7) este imposibila pentru ![]()
Pasul 4
![]()
Pasul 5
Problema
(2.7) este posibila pentru ![]() si
si ![]() .
.
Pasul 6
![]()
Pasul 4
![]()
Pasul 5
Problema
(2.7) este posibila pentru ![]() . Deci
. Deci ![]()
Pasul 6
![]()
Pasul 4
![]()
Pasul 5
Problema
(2.7) este posibila pentru ![]() si
si ![]() . Deci
. Deci ![]() .
.
Pasul 6
![]()
Pasul 4
![]()
Pasul 5
Problema
(2.7) este posibila pentru ![]() si
si ![]() . Deci
. Deci ![]() .
.
Pasul 6
![]()
Pasul 4
![]()
Pasul 5
Problema
(2.7) este posibila pentru ![]() si
si ![]() . Cum
. Cum ![]() ,
, ![]() .
.
Pasul 6
![]()
Dar problema (2.7) ![]() nu este extindere
minimala a problemei (2.7) pentru
nu este extindere
minimala a problemei (2.7) pentru ![]() si pasul 4 se executa
inca o data.
si pasul 4 se executa
inca o data.
Pasul 4
![]()
Pasul 5
Problema
(5.1.2.7) este posibila pentru ![]() si
si ![]() . Deci
. Deci ![]() .
.
Pasul 6
![]() . De aceea se verifica daca problema (2.7) pentru
. De aceea se verifica daca problema (2.7) pentru ![]() este o extindere
minimala a problemei (2.7) pentru
este o extindere
minimala a problemei (2.7) pentru ![]() . Cum raspunsul este pozitiv acesta este sfarsitul
algoritmului. Una dintre solutiile
. Cum raspunsul este pozitiv acesta este sfarsitul
algoritmului. Una dintre solutiile ![]() si
si ![]() este solutie optimala
pentru problema (2.1). Cum
este solutie optimala
pentru problema (2.1). Cum ![]() a doua solutie este
mai buna. Forma completa a acestei solutii este data de tabelul urmator.
a doua solutie este
mai buna. Forma completa a acestei solutii este data de tabelul urmator.
|
Primitor Distribuitor | |||
Tabelul 1
Cost total = 510
![]() ,
, ![]() ,
, ![]()
Pentru a ilustra
intregul pas 5 al algoritmului se arata cum problema (2.5) este construita si
rezolvata pentru o anumita valoare a parametrului. Fie ![]() . In acest caz:
. In acest caz: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, 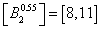 ,
, ![]() .
.
Problema (2.5) cu valori intervale pentru cerere si oferta poate fi redusa conform secventei 4 la o problema de transport cu rute interzise (data in tabelul 2) a carei solutie optimala este data in tabelul 3.
|
Oferta |
||||||||
|
| ||||||||
|
| ||||||||
|
|
|
| ||||||
|
Cerere |
Tabelul 2
|
Oferta |
||||||||
|
Cerere |
Tabelul 3
Solutia optimala a
problemei este redusa dupa aplicarea formulelor din finalul secventei 4 la
solutia problemei initiale (2.7) (ce este data in tabelul 1). De-a lungul
ultimei efectuari a pasului 6, in timpul verificarii conditiei de optim, ![]() (definit in definitia
2.5) este calculat din:
(definit in definitia
2.5) este calculat din:

Problema (2.7) pentru ![]() este analoaga cu cea
pentru
este analoaga cu cea
pentru ![]() ceea ce duce la
oprirea algoritmului.
ceea ce duce la
oprirea algoritmului.
Concluzii
S-a dat un algoritm pentru rezolvarea problemei fuzzy de transport (cu valori pentru cerere si oferta ca si pentru obiectivul fuzzy) in sensul maximizarii satisfacerii in comun a obiectivelor si a restrictiilor.
Acest algoritm necesita in afara unor transformari simple, doar rezolvarea problemei clasice de transport (in particular nu este necesar sa se rezolve problema cu parametru). Numerele fuzzy ce definesc problema nu trebuie sa fie trapezoidale.
1. R.R. Bellman si L.A.Zadeh, Decision - making in a fuzzy environment, Management Sci. B17 (1970), 203 - 218.
2. S.Chanas, Parametric techniques in fuzzy linear programming problems, in J.L Verdegay and M. Delgado, Eds., The Interface between Artificial Intellingence and Operations Research in Fuzzy Environment (Verlag TV Rheinland, Kln, 1989), 105 - 116.
3. R. Dombrowschi, Zagadnienia trasnportowe z parametryc - znymi ograniczeniami, Przeglad Statystyczny, XV (1968), 103 - 117.
4. D.Dubois si H. Prade, Operations on fuzzy numbers, Internat. J. Systems Sci. 6 (1978), 613 - 626.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1335
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved